Ребро куба ABCDA 1 B 1 C 1

Зарегистрируйтесь, чтобы просмотреть полный документ!

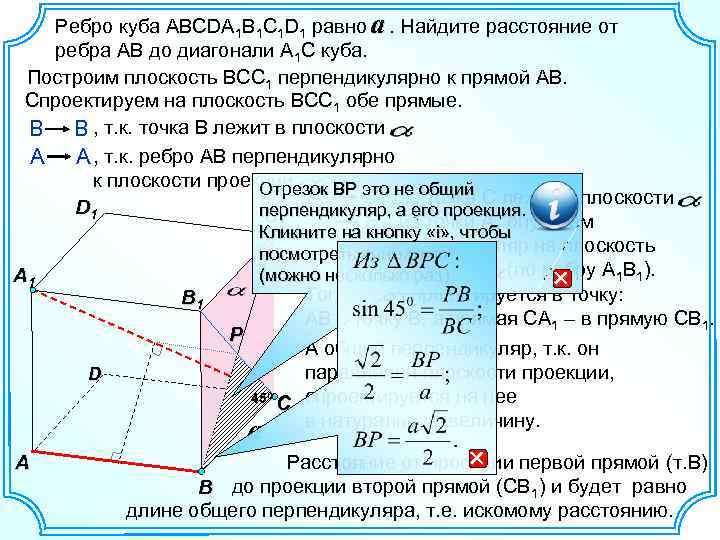
Ребро куба ABCDA 1 B 1 C 1 D 1 равно a. Найдите расстояние от ребра АВ до диагонали А 1 С куба. Построим плоскость ВСС 1 перпендикулярно к прямой АВ. Спроектируем на плоскость BСС 1 обе прямые. В В , т. к. точка В лежит в плоскости. А А , т. к. ребро АВ перпендикулярно к плоскости проекции. ВР это не общий Отрезок С С , т. к. точка С лежит в плоскости. D 1 перпендикуляр, а его проекция. С 1 , из «i» , чтобы А 1 кнопку точки А 1 опускаем Кликните на В 1 перпендикуляр на плоскость посмотреть анимацию проекции (по ребру А 1 В 1). (можно несколько раз). А 1 Тогда, АВ спроектируется в точку: В 1 АB в точку В, а прямая СA 1 – в прямую СВ 1. Р А общий перпендикуляр, т. к. он параллелен плоскости проекции, D 450 С спроектируется на нее в натуральную величину. a А Расстояние от проекции первой прямой (т. В) В до проекции второй прямой (СВ 1) и будет равно длине общего перпендикуляра, т. е. искомому расстоянию.

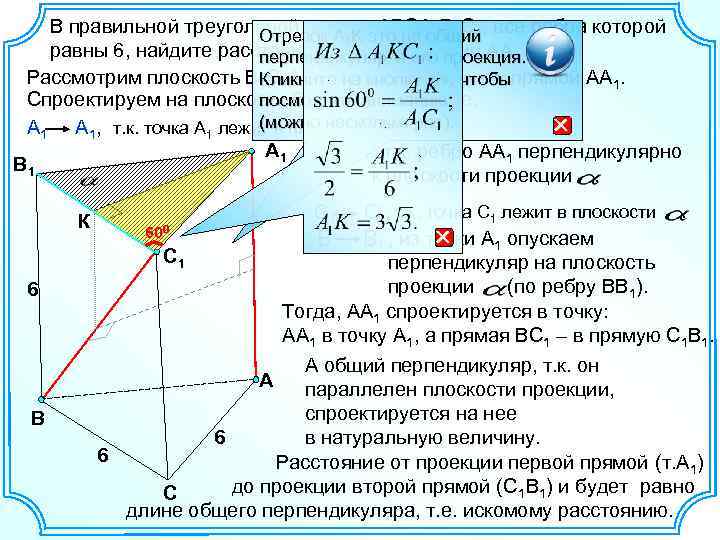
В правильной треугольной призмеэто не общий , все ребра которой Отрезок А 1 K ABCA 1 B 1 C 1 равны 6, найдите расстояние между прямыми АА 1 и ВС 1. перпендикуляр, а его проекция. Рассмотрим плоскость В 1 С 1 А 1 перпендикулярную к прямой АА 1. Кликните на кнопку «i» , чтобы Спроектируем на плоскость В 1 С 1 А 1 обе прямые. посмотреть анимацию (можно несколько А 1, т. к. точка А 1 лежит в плоскости. раз). А 1 А А 1 , т. к. ребро АА 1 перпендикулярно В 1 к плоскости проекции. К С 1, т. к. точка С 1 лежит в плоскости. В В 1 , из точки А 1 опускаем перпендикуляр на плоскость проекции (по ребру ВВ 1). Тогда, АА 1 спроектируется в точку: АА 1 в точку А 1, а прямая ВС 1 – в прямую С 1 В 1. С 1 600 С 1 6 А общий перпендикуляр, т. к. он параллелен плоскости проекции, спроектируется на нее 6 в натуральную величину. 6 Расстояние от проекции первой прямой (т. А 1) до проекции второй прямой (С 1 В 1) и будет равно С длине общего перпендикуляра, т. е. искомому расстоянию. А В

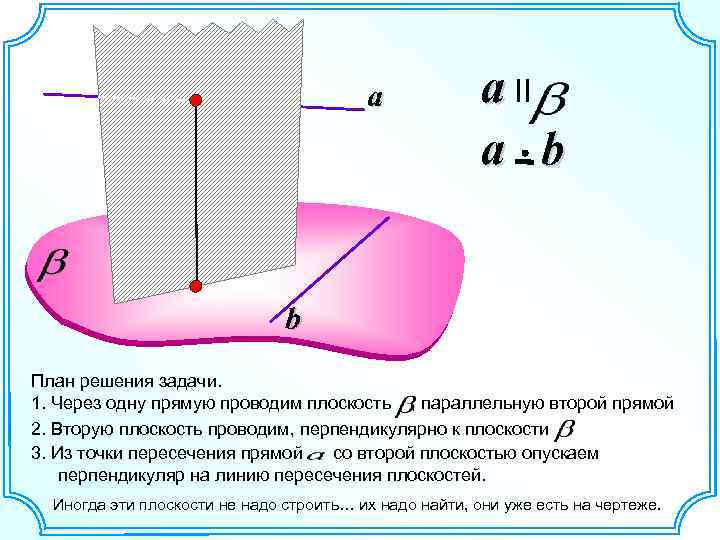
a a II a b b План решения задачи. 1. Через одну прямую проводим плоскость , параллельную второй прямой 2. Вторую плоскость проводим, перпендикулярно к плоскости 3. Из точки пересечения прямой со второй плоскостью опускаем перпендикуляр на линию пересечения плоскостей. Иногда эти плоскости не надо строить… их надо найти, они уже есть на чертеже.

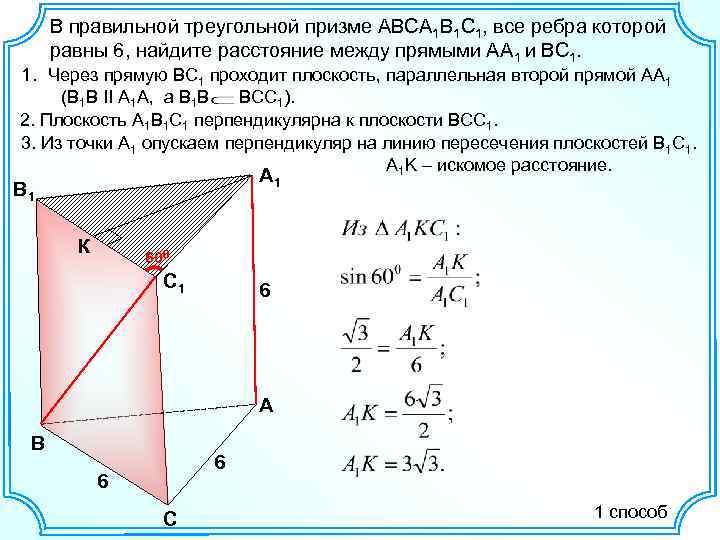
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 6, найдите расстояние между прямыми АА 1 и ВС 1. Через прямую ВС 1 проходит плоскость, параллельная второй прямой АА 1 (В 1 В II А 1 А, а В 1 В ВСС 1). 2. Плоскость А 1 B 1 С 1 перпендикулярна к плоскости ВСС 1. 3. Из точки А 1 опускаем перпендикуляр на линию пересечения плоскостей В 1 С 1. А 1 K – искомое расстояние. А 1 В 1 К 600 С 1 6 А В 6 6 С 1 способ

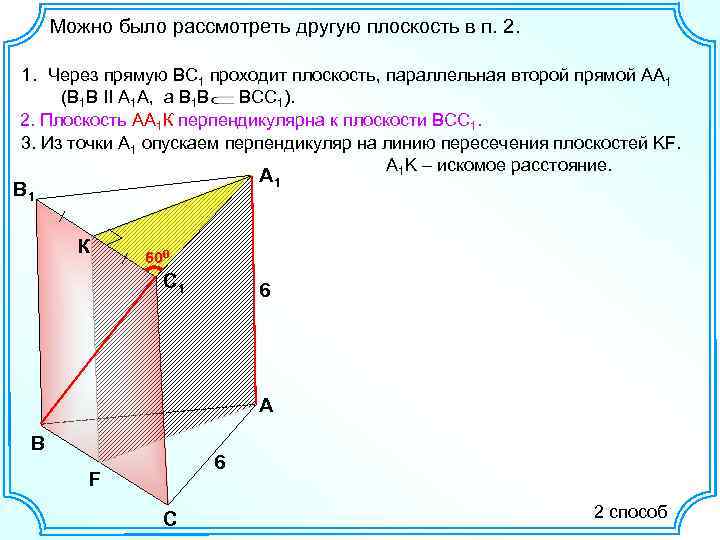
Можно было рассмотреть другую плоскость в п. 2. 1. Через прямую ВС 1 проходит плоскость, параллельная второй прямой АА 1 (В 1 В II А 1 А, а В 1 В ВСС 1). 2. Плоскость АА 1 К перпендикулярна к плоскости ВСС 1. 3. Из точки А 1 опускаем перпендикуляр на линию пересечения плоскостей KF. А 1 K – искомое расстояние. А 1 В 1 К 600 С 1 6 А В 6 F С 2 способ

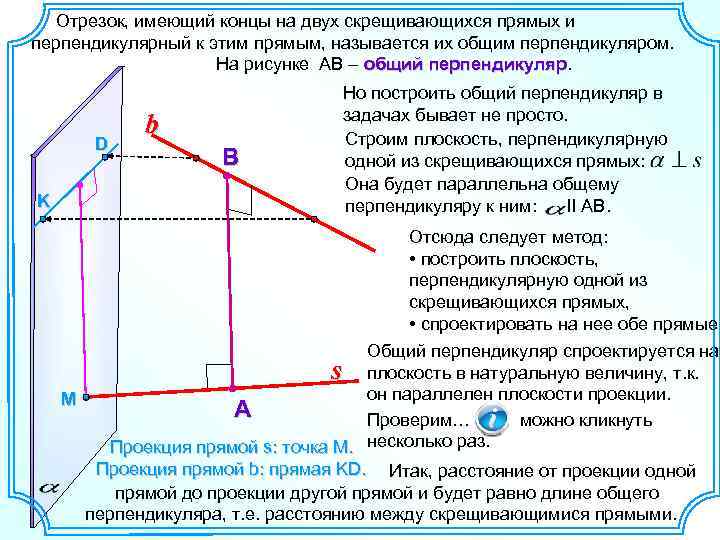
Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к этим прямым, называется их общим перпендикуляром. На рисунке АВ – общий перпендикуляр D K b В Но построить общий перпендикуляр в задачах бывает не просто. Строим плоскость, перпендикулярную одной из скрещивающихся прямых: Она будет параллельна общему перпендикуляру к ним: II AB. Отсюда следует метод: • построить плоскость, перпендикулярную одной из скрещивающихся прямых, • спроектировать на нее обе прямые. Общий перпендикуляр спроектируется на s плоскость в натуральную величину, т. к. он параллелен плоскости проекции. М А Проверим… можно кликнуть Проекция прямой s: точка М. несколько раз. Проекция прямой b: прямая KD. Итак, расстояние от проекции одной прямой до проекции другой прямой и будет равно длине общего перпендикуляра, т. е. расстоянию между скрещивающимися прямыми.

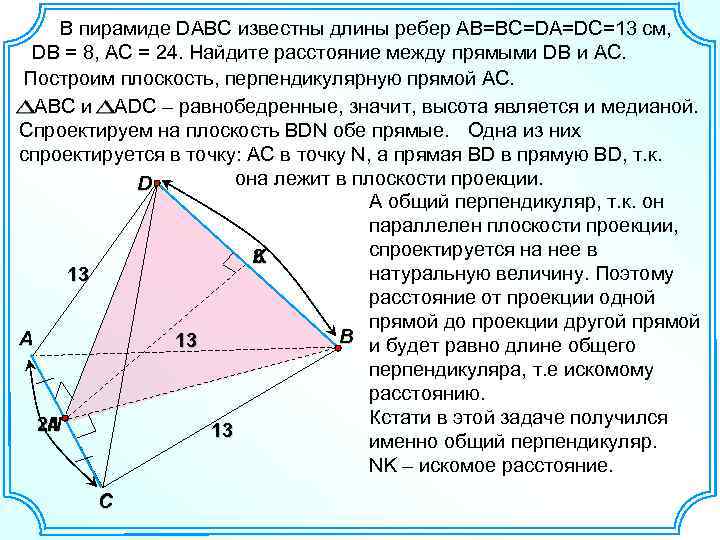
В пирамиде DABC известны длины ребер АВ=ВС=DA=DC=13 см, DB = 8, AC = 24. Найдите расстояние между прямыми DB и АС. Построим плоскость, перпендикулярную прямой АС. АВС и ADC – равнобедренные, значит, высота является и медианой. Спроектируем на плоскость BDN обе прямые. Одна из них спроектируется в точку: АC в точку N, а прямая BD в прямую BD, т. к. она лежит в плоскости проекции. D А общий перпендикуляр, т. к. он параллелен плоскости проекции, спроектируется на нее в K 8 натуральную величину. Поэтому 13 расстояние от проекции одной прямой до проекции другой прямой B и будет равно длине общего A 13 перпендикуляра, т. е искомому расстоянию. Кстати в этой задаче получился N 24 13 именно общий перпендикуляр. NK – искомое расстояние. C

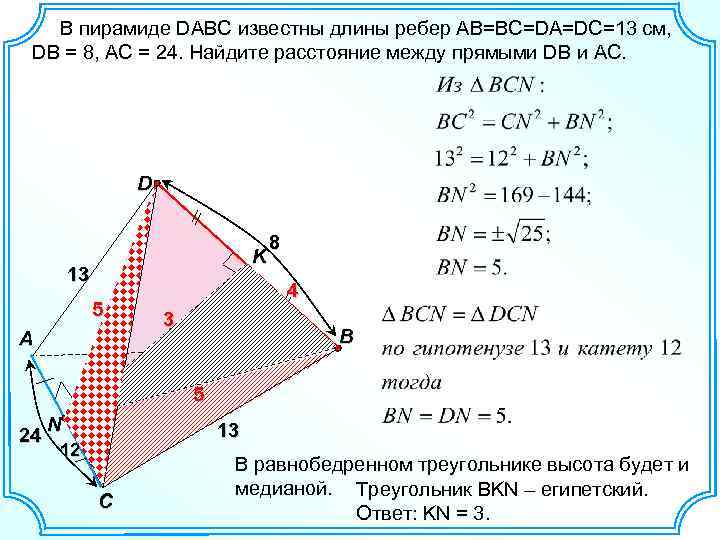
В пирамиде DABC известны длины ребер АВ=ВС=DA=DC=13 см, DB = 8, AC = 24. Найдите расстояние между прямыми DB и АС. D K 13 5 A 8 4 3 B 13 5 N 24 13 12 C В равнобедренном треугольнике высота будет и медианой. Треугольник BKN – египетский. Ответ: KN = 3.

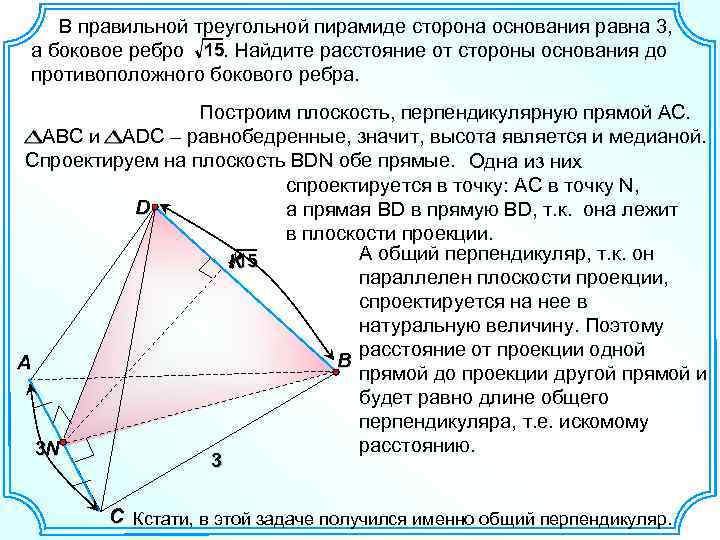
В правильной треугольной пирамиде сторона основания равна 3, а боковое ребро 15. Найдите расстояние от стороны основания до противоположного бокового ребра. Построим плоскость, перпендикулярную прямой АС. АВС и ADC – равнобедренные, значит, высота является и медианой. Спроектируем на плоскость BDN обе прямые. Одна из них спроектируется в точку: АC в точку N, D а прямая BD в прямую BD, т. к. она лежит в плоскости проекции. А общий перпендикуляр, т. к. он 15 K параллелен плоскости проекции, спроектируется на нее в натуральную величину. Поэтому расстояние от проекции одной B A прямой до проекции другой прямой и будет равно длине общего перпендикуляра, т. е. искомому расстоянию. 3 N 3 C Кстати, в этой задаче получился именно общий перпендикуляр.

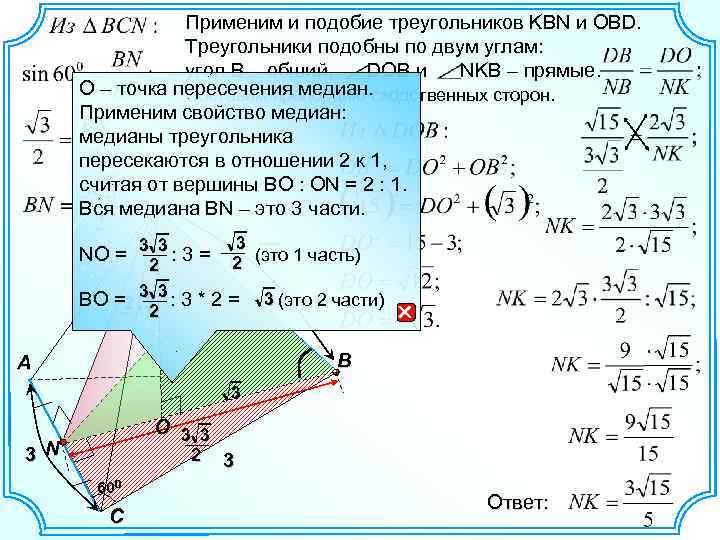
Применим и подобие треугольников KBN и OBD. Треугольники подобны по двум углам: угол B – общий, DOB и NKB – прямые. О – точка пересечения медиан. сходственных сторон. Составим пропорцию Применим свойство медиан: медианы треугольника пересекаются в отношении 2 к 1, считая от вершины BO : ON = 2 : 1. D Вся медиана BN – это 3 части. 3 NО = 3 3 : 3 = K (это 1 часть) 2 15 2 BО =2 3 3 : 3 * 2 = 3 2 3 (это 2 части) B A 3 O 3 3 3 N 2 600 C 3 Ответ:

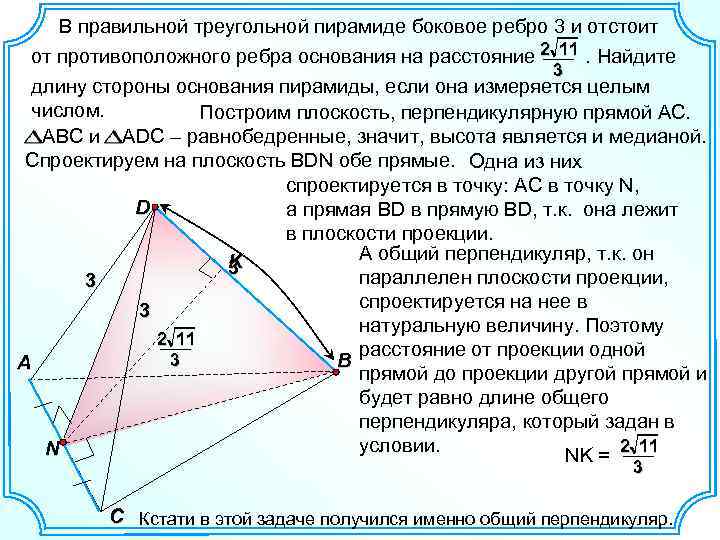
В правильной треугольной пирамиде боковое ребро 3 и отстоит от противоположного ребра основания на расстояние 2 11. Найдите 3 длину стороны основания пирамиды, если она измеряется целым числом. Построим плоскость, перпендикулярную прямой АС. АВС и ADC – равнобедренные, значит, высота является и медианой. Спроектируем на плоскость BDN обе прямые. Одна из них спроектируется в точку: АC в точку N, D а прямая BD в прямую BD, т. к. она лежит в плоскости проекции. А общий перпендикуляр, т. к. он K 3 параллелен плоскости проекции, 3 спроектируется на нее в 3 натуральную величину. Поэтому 2 11 расстояние от проекции одной 3 B A прямой до проекции другой прямой и будет равно длине общего перпендикуляра, который задан в условии. N NK = 2 11 3 C Кстати в этой задаче получился именно общий перпендикуляр.

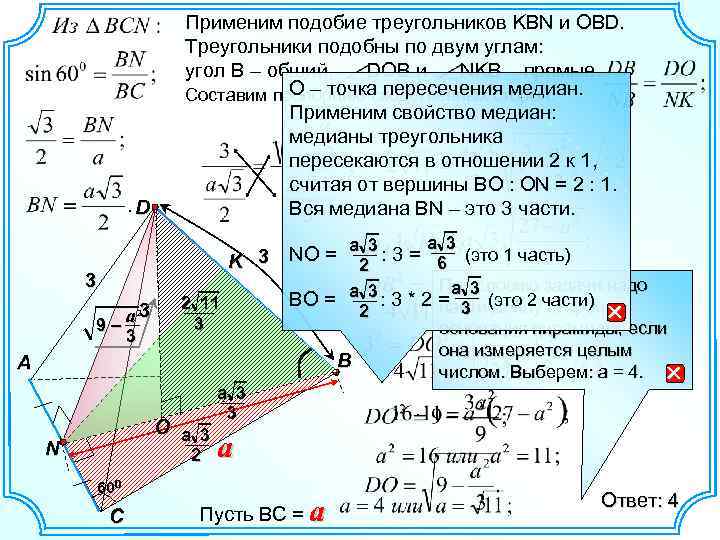
D Применим подобие треугольников KBN и OBD. Треугольники подобны по двум углам: угол B – общий, DOB и NKB – прямые. О – точка пересечения медиан. Составим пропорцию сходственных сторон. Применим свойство медиан: медианы треугольника 3 пересекаются в отношении 2 к 1, * 2 считая от вершины BO : ON = 2 : 1. Вся медиана BN – это 3 части. a 3 3 NО = 2 : 3 = 6 (это 1 часть) K 3 a 23 9– 3 2 11 3 A O a 3 N 2 a 3 3 По условию задачи надо a 3 BО = : 3 * 2 = 3 (это 2 части) найти длину стороны 2 основания пирамиды, если она измеряется целым B ^ а числом. Выберем: 2 = 4. a 600 C Пусть ВС = a Ответ: 4

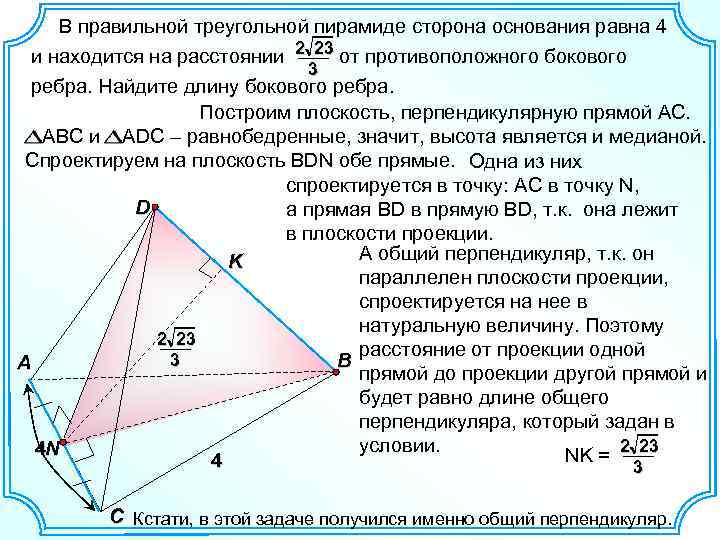
В правильной треугольной пирамиде сторона основания равна 4 и находится на расстоянии 2 23 от противоположного бокового 3 ребра. Найдите длину бокового ребра. Построим плоскость, перпендикулярную прямой АС. АВС и ADC – равнобедренные, значит, высота является и медианой. Спроектируем на плоскость BDN обе прямые. Одна из них спроектируется в точку: АC в точку N, D а прямая BD в прямую BD, т. к. она лежит в плоскости проекции. А общий перпендикуляр, т. к. он K параллелен плоскости проекции, спроектируется на нее в натуральную величину. Поэтому 2 23 расстояние от проекции одной 3 B A прямой до проекции другой прямой и будет равно длине общего перпендикуляра, который задан в условии. 4 N NK = 2 23 4 3 C Кстати, в этой задаче получился именно общий перпендикуляр.

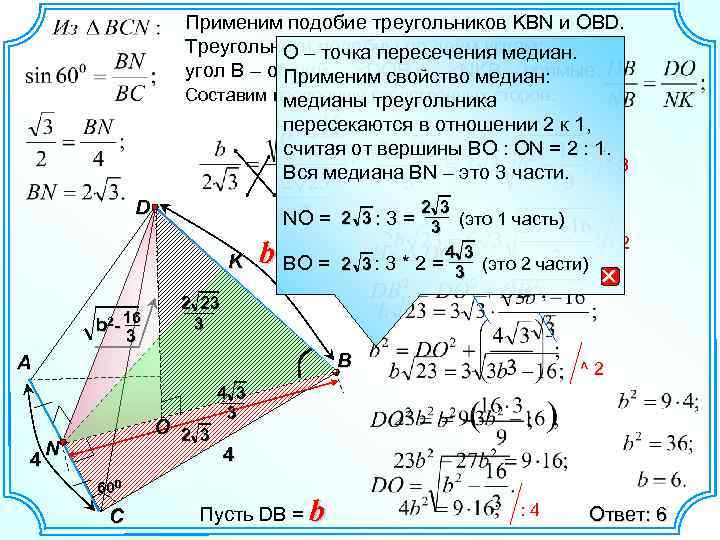
Применим подобие треугольников KBN и OBD. Треугольники подобны по двум углам: О – точка пересечения медиан. угол B – общий, DOB и NKB – прямые. Применим свойство медиан: Составим пропорцию сходственных сторон. медианы треугольника пересекаются в отношении 2 к 1, 3 считая от вершины BO : ON = 2 : 1. *3 Вся медиана BN – это 3 части. D 2 3 NО = 2 3 : 3 = 3 (это 1 часть) K b 2 - 16 b- 3 b BО = 4 3 2 3 : 3 * 2 = 3 (это 2 части) B O 2 3 ^2 4 3 3 4 600 C 2 23 3 A N 4 : 2 Пусть DВ = b : 4 Ответ: 6

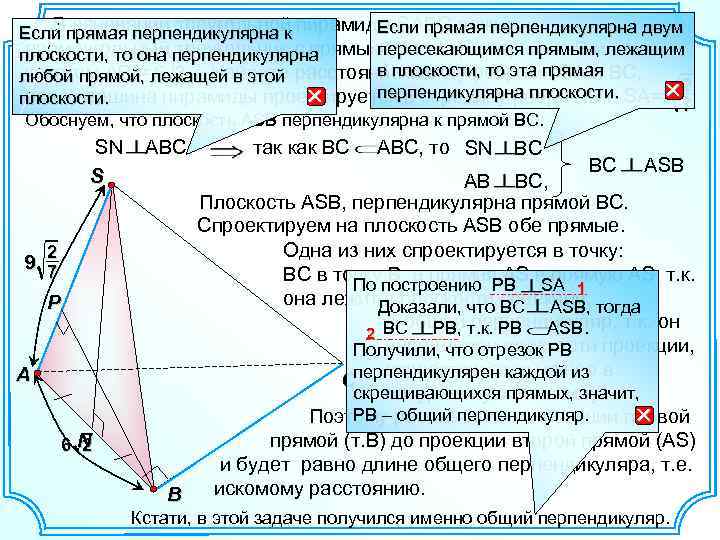
В основании треугольной Если прямая перпендикулярна двум Если прямая перпендикулярна к пирамиды SABC лежит пересекающимся прямым, прямоугольный треугольник с прямым углом при вершине В илежащим плоскости, то она перпендикулярна в плоскости, то эта прямая катетом АВ = 6 2. Найдите любой прямой, лежащей в этой расстояние между ребрами SA и BC, 2 перпендикулярна плоскости. если вершина пирамиды проектируется в середину ребра АВ и SA=9 7 плоскости. Обоснуем, что плоскость ASB перпендикулярна к прямой BС. SN S 2 9 7 P A 6 N 2 AВC так как ВС АВС, то SN BC ВC ASB АВ ВС, Плоскость ASB, перпендикулярна прямой ВС. Спроектируем на плоскость ASB обе прямые. Одна из них спроектируется в точку: BC в точку B, а прямая AS в прямую AS, т. к. По построению PВ SA 1 она лежит. Доказали, что проекции. тогда в плоскости ВC ASB, А общий т. к. PB ASB. PB, перпендикуляр, т. к. он 2 ВС параллелен плоскости проекции, Получили, что отрезок PB спроектируется на нее в Cперпендикулярен каждой из скрещивающихся прямых, значит, натуральную величину. РВ – общий перпендикуляр. Поэтому расстояние от проекции первой прямой (т. В) до проекции второй прямой (АS) и будет равно длине общего перпендикуляра, т. е. искомому расстоянию. B Кстати, в этой задаче получился именно общий перпендикуляр.

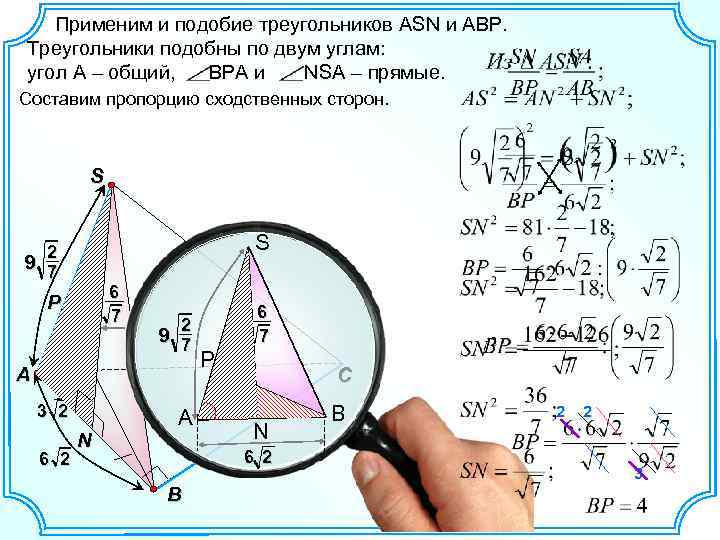
Применим и подобие треугольников ASN и ABP. Треугольники подобны по двум углам: угол A – общий, BPA и NSA – прямые. Составим пропорцию сходственных сторон. S S 2 9 7 6 7 P 2 9 7 A 3 2 6 2 N A 6 7 P C N 6 2 B В 2 2 3

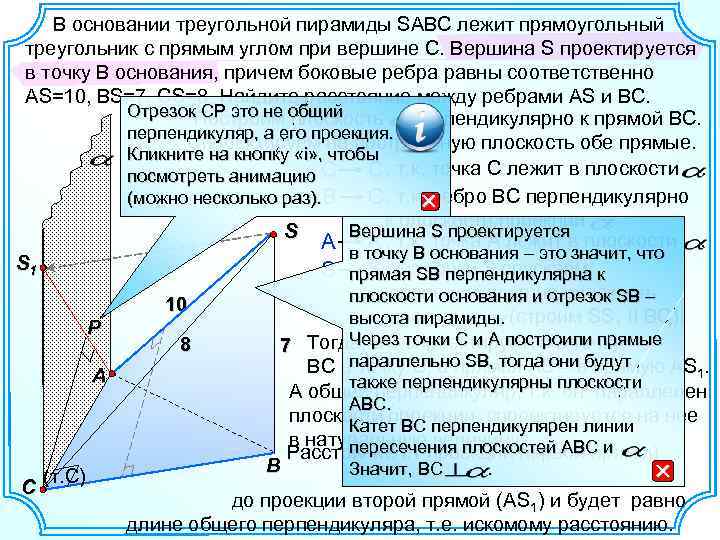
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине С. Вершина S проектируется в точку В основания, причем боковые ребра равны соответственно AS=10, BS=7, CS=8. Найдите расстояние между ребрами AS и ВС. Отрезок. Построим общий СР это не плоскость перпендикулярно к прямой ВС. перпендикуляр, а его проекция. Спроектируем на построенную плоскость обе прямые. Кликните на кнопку «i» , чтобы С , т. к. точка С лежит в плоскости. посмотреть анимацию С ребро ВС перпендикулярно (можно несколько раз). В С , т. к. к плоскости проекции. Вершина S проектируется S А в точку В основания – это в плоскости. А , т. к. точка А лежит значит, что S 1 S прямая SB перпендикулярна к S 1, из точки S опускаем перпендикуляр на плоскость плоскости основания и отрезок SB – 10 проекции высота пирамиды. (строим SS 1 II BC). P Через спроектируется в точку: 8 7 Тогда, ВС точки С и А построили прямые BC впараллельно SB, тогда онивбудут точку С, а прямая AS – прямую AS 1. A также перпендикулярны А общий перпендикуляр, т. к. плоскости он параллелен АВС. плоскости проекции, спроектируется на нее Катет ВС перпендикулярен линии в натуральную величину. пересечения плоскостей АВС и Расстояние от проекции первой прямой B Значит, ВС. (т. С) C до проекции второй прямой (АS 1) и будет равно длине общего перпендикуляра, т. е. искомому расстоянию.

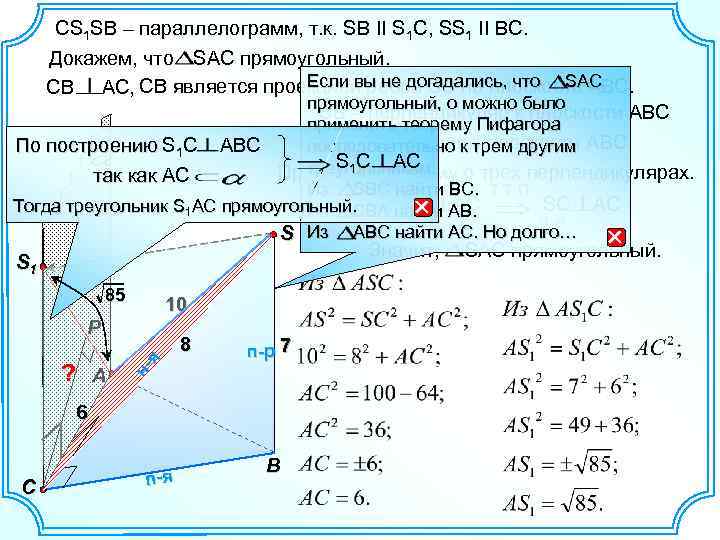
СS 1 SВ – параллелограмм, т. к. SB II S 1 C, SS 1 II BC. Докажем, что SAC прямоугольный. Если вы не догадались, что SAC СВ АС, СВ является проекцией ребра SC на плоскость ABС. прямоугольный, о можно было SB – перпендикуляр к плоскости ABС применить теорему Пифагора SC – наклонная к плоскости последовательно к трем другим ABС. По построению S 1 С АВС S 1 С AС треугольникам: Применим теорему о трех перпендикулярах. так как АС Из SBC найти BC. Т Т П ВС АС SC AC Тогда треугольник S 1 AC прямоугольный. SBA найти АВ. Из п-я н-я S Из АВС найти АС. Но долго… Значит, S 1 85 10 P ня ? A 8 п-р 7 6 C п-я B SAC прямоугольный.

Скачать презентацию Ребро куба ABCDA 1 B 1 C 1

C_2 стереометрия расстояние между прямыми.ppt

Количество слайдов: 18