РЕАЛЬНІ ГАЗИ Заступник директора Інституту інформатики,

РЕАЛЬНІ ГАЗИ Заступник директора Інституту інформатики, завідувач кафедри комп ’’ ютерної інженерії , , доктор педагогічних наук, професор Сергієнко Володимир Петрович сайт www. npu. edu. ua/ebook/ Е-Е- mail : : sergienkovp@mail. ruru

План 1. 1. Відхилення реальних газів від законів для ідеальних газів. 2. 2. Сили міжмолекулярної взаємодії. 3. 3. Рівняння Ван-дер-Ваальса та його аналіз. 4. 4. Порівняння ізотерм Ван-дер-Ваальса з експериментальними ізотермами. Інші рівняння стану реальних газів.

Література: 1. Кучерук І. М. , Горбачук І. Т. , Луцик П. П. Загаль-ний курс фізики: Навч. посібник. – Т. 1. : Механіка. Молекулярна фізика і термодинаміка. – К. : Техні-ка, 1999. – 536 с. (с. 419 – 432). 2. 2. CC ергієнко В. П. Курс фізики: Навч. посібник. – К. : Майстер-клас, 2006. – 152 с. (с. 66 – 76). 3. Сергієнко В. П. , Шут М. І. та ін. Демонстраційний експеримент з фізики: Навч. посібник. – К. “Просвіта”: , 2006. – 368 с. 4. 4. Загальна фізика. Програма навчальної дисцип-ліни для студентів вищих педагогічних закладів освіти / М. І. Шут, І. Т. Горбачук, В. П. Сергієнко. – К. : НПУ, 2005. – 48 с. 55. . www. npu. edu. ua/ebook //

Відхилення реальних газів від законів для ідеальних газів Експериментально доведено, що закони ідеального газу виконуються при низьких тисках і порівняно високих температурах. В таблиці 9. 1 приведені результати експериментальної пере-вірки закону Бойля-Маріотта. p. V = = const (9. 1)1) Таблиця 9. 1 Результати експериментальної перевірки закону Бойля-Маріотта для певної маси азоту при TT = 273 К рр , 10 55 Па Па рр VV , 10 22 Па Па мм 33 , , 1010 22 Па Па мм 33 11 1, 0001, 000 100100 0, 994 1, 000 200200 1, 048 1, 009 500500 1, 390 1, 014 1000 2, 069 0, 8932( + )( ) a p V b V

Чи можна не враховувати розмір молекул в реальному газі ? Якщо створити тиск в 100 атм, то власний об’єм молекул складатиме від всього об’єму, в 1000 атм – – . Отже, такий об’єм буде зайнятий для руху молекул, тому нехтувати розмірами молекул не можна. — 10 3 — 30 3 0 4 ~ 10 м, = 4, 2 10 м 3 r V r 1 100 1 10 в в 11 мм 33 N = 2, 7∙ 10 2525 (м(м 33 )) -1 -1 — число Лошмідта за за нормальних умов. (( 11 атм, 0° 0° C) C) — 4 3 0 1, 1 10 м вл. V = V N

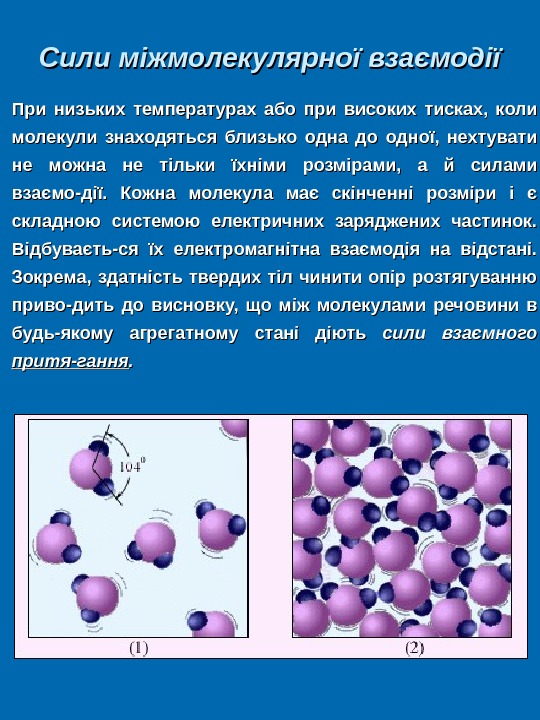
Сили міжмолекулярної взаємодії При низьких температурах або при високих тисках, коли молекули знаходяться близько одна до одної, нехтувати не можна не тільки їхніми розмірами, а й силами взаємо-дії. Кожна молекула має скінченні розміри і є складною системою електричних заряджених частинок. Відбуваєть-ся їх електромагнітна взаємодія на відстані. Зокрема, здатність твердих тіл чинити опір розтягуванню приво-дить до висновку, що між молекулами речовини в будь-якому агрегатному стані діють сили взаємного притя-гання. .

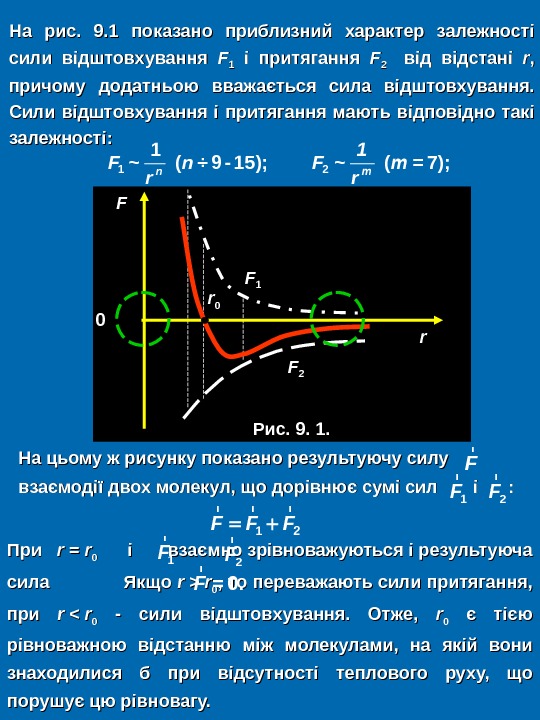
На цьому ж рисунку показано результуючу силу взаємодії двох молекул, що дорівнює сумі сил і і : : На рис. 9. 1 показано приблизний характер залежності сили відштовхування FF 11 і притягання FF 2 2 від відстані rr , , причому додатньою вважається сила відштовхування. Сили відштовхування і притягання мають відповідно такі залежності: r Fn m 1 F n F m r r 1 2 1 ~ ( ÷ 9 — 15); ~ ( = 7); r 1 F r 2 F r r r 1 2 F F F При rr = = rr 00 і взаємно зрівноважуються і результуюча сила Якщо rr >> rr 00 , то переважають сили притягання, при rr << rr 00 — сили відштовхування. Отже, rr 00 є тією рівноважною відстанню між молекулами, на якій вони знаходилися б при відсутності теплового руху, що порушує цю рівновагу. r = 0. F r 1 F r 2 F rrrr 00 FF 00 Рис. 9. 1.

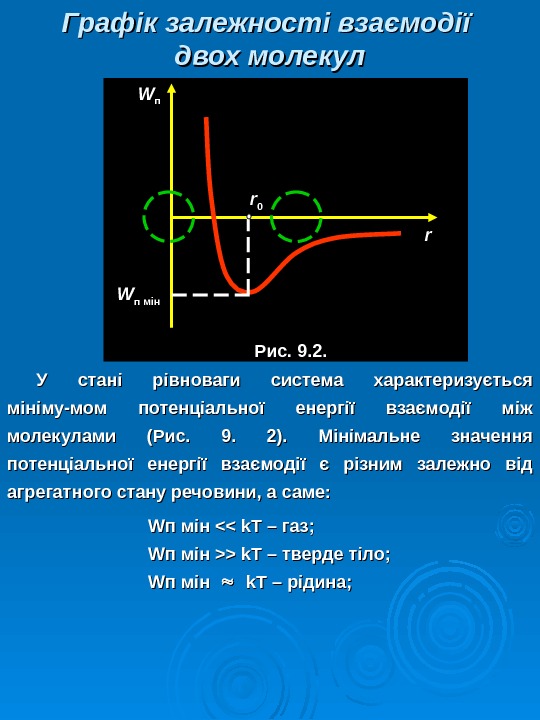
Графік залежності взаємодії двох молекул У стані рівноваги система характеризується мініму — мом потенціальної енергії взаємодії між молекулами (Рис. 9. 2). Мінімальне значення потенціальної енергії взаємодії є різним залежно від агрегатного стану речовини, а саме: WW п мін <> k. T – тверде тіло; WW п мін k. T – – рідина; rrrr 00 WW пп WW п мін Рис. 9. 2.

Рівняння Ван-дер-Ваальса та його аналіз Вперше врахував вплив молекулярних сил і, користуючись моделлю молекул, як твердих пружних куль (рис. 9. 3), вніс поправки до рівняння стану ідеального газу в 1873 р. у праці «Про неперервність газоподібного і рідкого станів» нідерландський фізик Ван-дер-Ваальс (1837 – 1923). Рис. 9. 3.

Рівняння Ван-дер-Ваальса та його аналіз. Знайдемо значення об’єму bb. Уявимо собі посудину в формі куба, об’ємом VV ММ , який займає 1 моль газу за даних тиску і температури. (рис. 9. 4) Сторона куба дорівнює . Нехай діаметр молекули дорівнює dd , а радіус rr = . Припустимо, що спочатку в нашій посудині міститься всього одна молекула. Для її руху (точніше для руху її центра) доступним є увесь об’єм посудини, за вирахунком шару товщиною rr , що прилягає до стінки. Наша молекула може рухатися в об’ємі куба зі стороною на dd менше ніж сторона посуди — ни. Цей об’єм дорівнює: 3 MV 2 d 33( — )MV d dd rr. VV MM Рис. 9. 4.

Введемо другу молекулу. Пунктиром показано об’єм, який оточує кожну молекулу, в який не може потрапити центр іншої молекули. Цей об’єм дорівнює . Для довільної з двох молекул виявляється доступним об’єм, що дорівнює . 34 3 d 3 3 3 4 ( ) 3 M V d d Якщо ввести в посудину ще і третю молекулу, то для будь-якої молекули вільним буде об’єм 3 334 ( ) 2. 3 MV d d Нарешті, коли в посудині опиняться всі NN АА молекул, які містяться в 1 молі газу , то кожна з них матиме можли-вість рухатися в об’ємі 3 3 3 4 ( ). 3 M A V d N d Якщо врахувати ту обставину, що під час зближення двох молекул для кожної з них суттєвої є тільки половина забороненої сфери (напівсфера), яка повернена до неї, тоді вільним для руху будь-якої молекули виявиться такий об’єм 3 3 3 4 = ( ). 2 3 A M N V V d d При dd << << , як це завжди буває, одержимо: 3 MV 3 32 4 = = 4. 3 3 M A M AV V N d V N r Отже, 34 = 4 (9. 3) 3 Ab N r

де Це і є рівняння стану реального газу або рівняння Ван-дер-Ваальса для 1 моля реального газу. А для довільної маси газу mm : : =MV VДія сил притягання між молекулами реального газу вик-ликає його додаткове стиснення, створюючи тим самим додатковий внутрішній тиск pp ii . Тому фактичний тиск реального газу біде більшим pp і дорівнюватиме pp + + pp ii. Підставляючи це значення замість pp в формулу (9. 2) одержуємо: (( pp + + pp ii )()( VV М М bb ) ) = = RTRT (9. 4) Внутрішній тиск pp ii , направлений так як і зовнішній тиск pp , , всередину газу буде пропорційним як числу молекул, що притягують ( nn ), так і числу молекул, що притягуються ( nn ) ) в одиниці об’єму газу, тобто: 2 2= = = (9. 5) А i М МN a p αn α V V де а – стала, яка характеризує сили молекулярного притягання в газі 6 2 Па м моль Підставляючи вираз для pp ii в формулу (9. 4), одержуємо : : 2+ = (9. 6) М Мa p V b RT V 2 2 2+ = (9. 7) m a m m p V b RT M V M M де де VV – об’єм маси газу, MM – молярна маса газу.

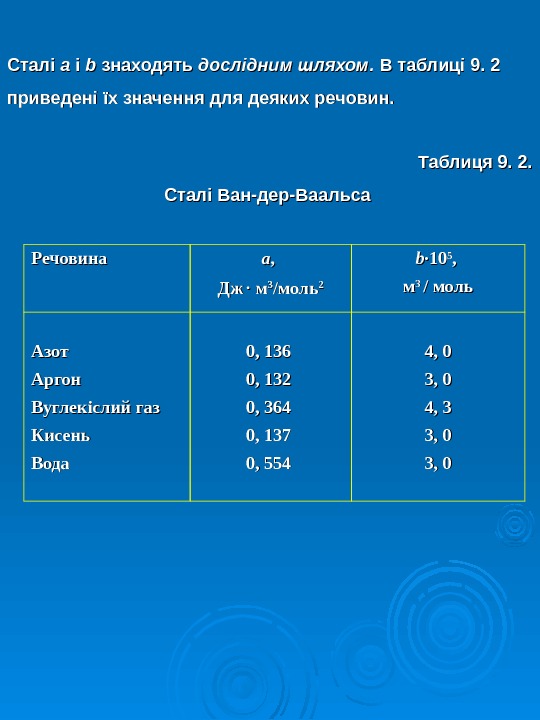
Сталі a a і і bb знаходять дослідним шляхом. В таблиці 9. 2 приведені їх значення для деяких речовин. Таблиця 9. 2. Сталі Ван-дер-Ваальса Речовина aa , , Дж. Дж мм 33 // моль 22 b∙b∙ 1010 55 , , мм 3 3 / / моль Азот Аргон Вуглекіслий газ Кисень Вода 0, 136 0, 132 0, 364 0, 137 0, 554 4, 0 3, 0 4, 3 3, 03,

Найбільш повні якісні результати з рівняння Ван-дер-Ваальса можна дістати шляхом аналізу його ізотерм, по — будованих за формулою (9. 6). Розкриємо дужки в 9. 6 і для довільних температур Т дістанемо 3 2( + ) + = 0 M M Mp. V bp RT V ab абоабо 3 2( + ) + = 0 (9. 8)M M M RT a ab V V p p p Це рівняння матиме 3 корені розв’язку. Може бути: 1) 1 корінь дійсний 2 уявні – відповідає надкритичним тискам. 2) Всі 3 корені дійсні — різні – докритичним Т < Т кк . . 3) Всі 3 корені дійсні і рівні між собою – це відповідає критичному стану.

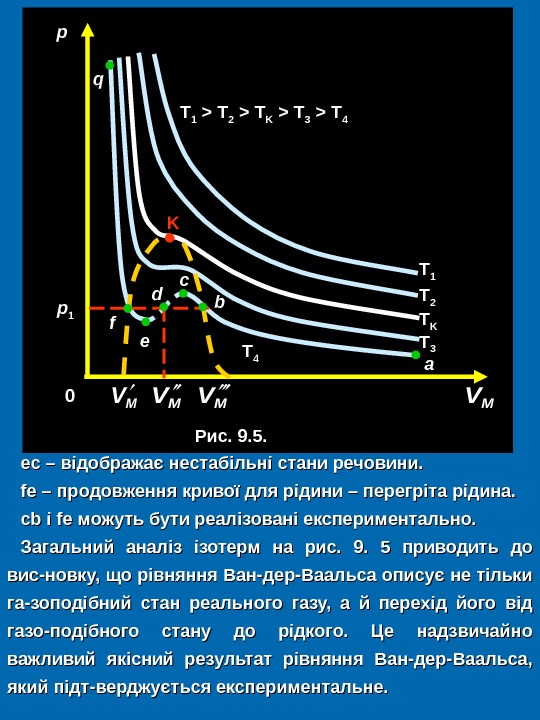
ес – відображає нестабільні стани речовини. fе – продовження кривої для рідини – перегріта рідина. сс bb і f ee можуть бути реалізовані експериментально. Загальний аналіз ізотерм на рис. 99. . 55 приводить до вис-новку, що рівняння Ван-дер-Ваальса описує не тільки гага — зоподібний стан реального газу, а й перехід його від газо — подібного стану до рідкого. Це надзвичайно важливий якісний результат рівняння Ван-дер-Ваальса, який підт — верджується експериментальне. р р 1 0 K T 3 T 4 T K T 2 T 1 Рис. 9. 5. T 1 > T 2 > T K > T 3 > T 4 f e d с b a MVMVq

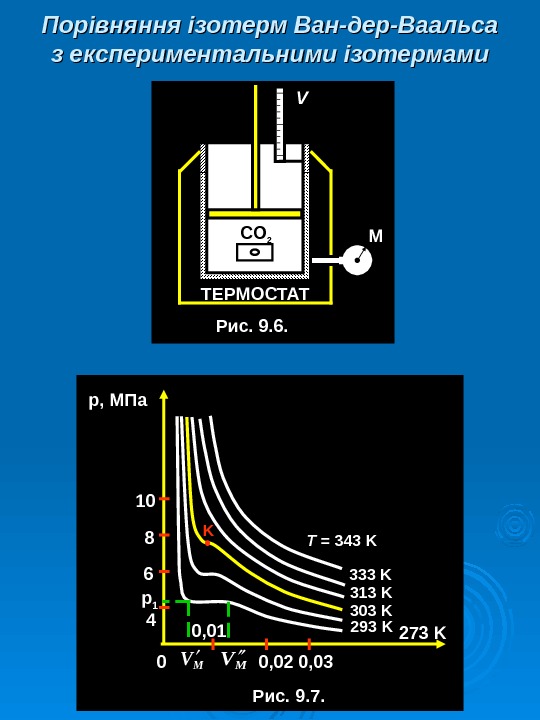
ТЕРМОСТАТ CO 2 МV Рис. 9. 6. Порівняння ізотерм Ван-дер-Ваальса з експериментальними ізотермами р 1 р , МПа 0 T = 3 4 3 K Рис. 9. 7. 10 8 6 4 0, 01 0, 02 0, 0 3 K 333 K 313 K 3 03 K 293 K 2 7 3 K M VMV

Рівняння стану реальних газів 1. Рівняння Дитерічі характерне тим, що воно додатко — во враховує вплив пристінного молекулярного шару на стан газу: ( ) = exp. M M a p V b RT RTV 2. Особливістю рівнянь Бертло і Клаузіуса є те, що вони чисто емпірично враховують залежність внут — рішнього тиску газу від температури. Рівняння Берт — ло записується так: 2+ ( ) = M Ma p V b RT TV 3. Рівняння Клаузіуса: M 2 M+ ( ) = ( + ) a p V b RT T V c Константи aa , , bb , , c c визначаються дослідно. 4. Рівняння Камерлінг-Оннеса L M M MB (T) p. V = RT + + + V V 2 3 21 5. Зведене рівняння 2 3 + (3 1) = 8 деде к p p , = , М к V V к. T. T