Реализация новых ФГОС по математике в основной школе

Реализация новых ФГОС по математике в основной школе. Яковлева Т. Л. , учитель математики, МОБУ «СОШ № 62» г. Оренбург

Рабочая программа по алгебре 7 класс ( базовый уровень)

Программа разработана на основе • Федерального государственного образовательного стандарта основного общего образования; • Примерной программы основного общего образования по математике; • Авторской программы по алгебре А. Г. Мордковича; • ООП МОБУ «СОШ № 62»

Отличительные особенности ФГОС В основе ФГОС лежит системно-деятельностный подход, предполагающий разнообразие индивидуальных образовательных траекторий Индивидуализация каждого ребенка, независимо от его психо-соматических способностей

Отличительные особенности ФГОС Основная цель – развитие личности на основе УУД, освоение и познание мира

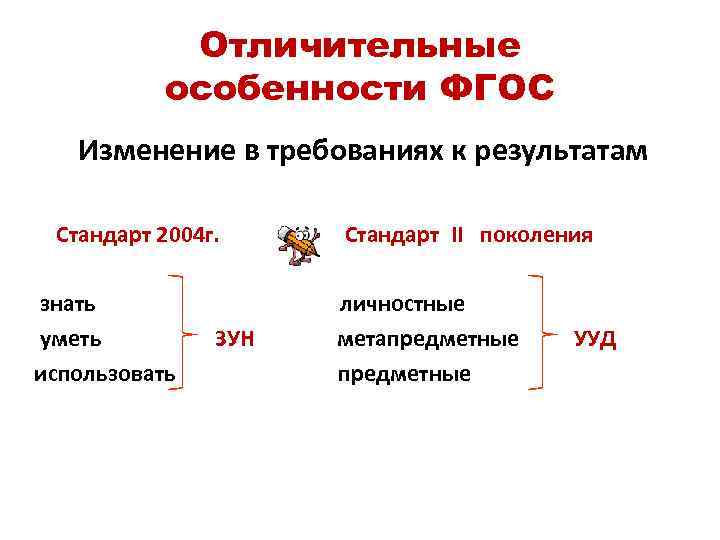Отличительные особенности ФГОС Изменение в требованиях к результатам Стандарт 2004 г. знать уметь использовать ЗУН Стандарт II поколения личностные метапредметные УУД

Новые ФГОС изменение метода обучения (с объяснительного на деятельностный) изменение оценки результатов обучения (оценка не только предметных ЗУН, но и метапредметных и личностных результатов)

Требования к уроку Традиционный урок Урок современного типа Объявление темы урока Учитель сообщает учащимся Формулируют сами учащиеся (учитель подводит учащихся к осознанию темы) Сообщение целей и задач Учитель формулирует и сообщает учащимся, чему должны научиться Формулируют сами учащиеся, определив границы знания и незнания (учитель подводит учащихся к осознанию целей и задач) Планирование Учитель сообщает учащимся, какую работу они должны выполнить, чтобы достичь цели Планирование учащимися способов достижения намеченной цели (учитель помогает, советует)

Практическая Под руководством учителя Учащиеся осуществляют учебные деятельность учащиеся выполняют ряд действия по намеченному плану учащихся практических задач (чаще (применяется групповой, применяется индивидуальный методы), фронтальный метод учитель консультирует организации деятельности) Осуществление контроля Учитель осуществляет контроль за выполнением учащимися практической работы Осуществле. Учитель в ходе ние коррекции выполнения и по итогам выполненной работы учащимися осуществляет коррекцию Учащиеся осуществляют контроль (применяются формы самоконтроля, взаимоконтроля), учитель консультирует Учащиеся формулируют затруднения и осуществляют коррекцию самостоятельно, учитель консультирует, советует, помогает

Оценивание учащихся Учитель осуществляет оценивание работы учащихся на уроке Учащиеся дают оценку деятельности по её результатам (самооценка, оценивание результатов деятельности товарищей), учитель консультирует Итог урока Учитель выясняет у учащихся, что они запомнили Проводится рефлексия Домашнее задание Учитель объявляет и комментирует (чаще – задание одно для всех) Учащиеся могут выбирать задание из предложенных учителем с учётом индивидуальных возможностей

В Федеральном базисном образовательном плане на изучение алгебры в 7 классе отводится 3 часа в неделю, всего – 102 часа, в том числе на проведение контрольных работ – 8 часов. Проектно - исследовательская деятельность, олимпиадное движение- во внеурочное время

Результаты изучения предмета: • личностные: • ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; • формирования коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой и других видах деятельности; • формирование представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации; • умения ясно и точно излагать свои мысли; развития креативного мышления.

Результаты изучения предмета: • метапредметные: • 1) умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности; • 2) умение самостоятельно планировать пути достижения целей, в том числе альтернативные, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; • 3) умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;

Результаты изучения предмета: • метапредметные: • 4) умение устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения и выводы; • 5) умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач; • 6) умение оценивать правильность выполнения учебной задачи, собственные возможности её решения; • 7) развития способности организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение: • 8)формирование учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий

Результаты изучения предмета: • предметные: • 1) формированея представлений о математике как о методе познания действительности, позволяющем описывать и изучать реальные процессы и явления; • 2) развитея умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования, доказательства математических утверждений; • 3) овладение символьным языком алгебры, решения линейных уравнений, систем линейных уравнений;

Результаты изучения предмета: • предметные: • 4) овладение элементами системы функциональных понятий, развитие умения использовать функционально-графические представления для решения некоторых математических задач, для описания и анализа реальных зависимостей; • 5) развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, компьютера, пользоваться оценкой и прикидкой при практических расчётах;

В ходе освоения содержания курса учащиеся получают возможность: • сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру; • овладеть символическим языком алгебры, выработать формальнооперативные алгебраические умения и научиться применять их к решению математических и нематических задач; • изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей; • развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства; • сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Урок проблема противоречи е гипотез а

Как проверить достижение новых образовательных результатов?

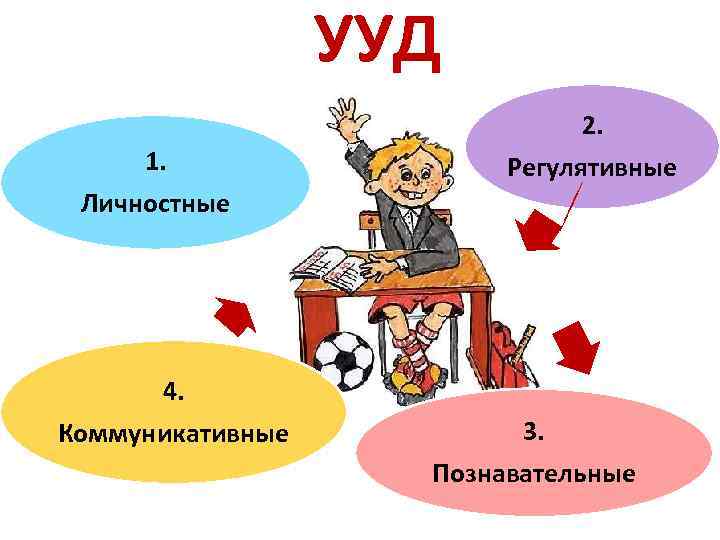УУД 1. Личностные 2. Регулятивные 4. Коммуникативные 3. Познавательные

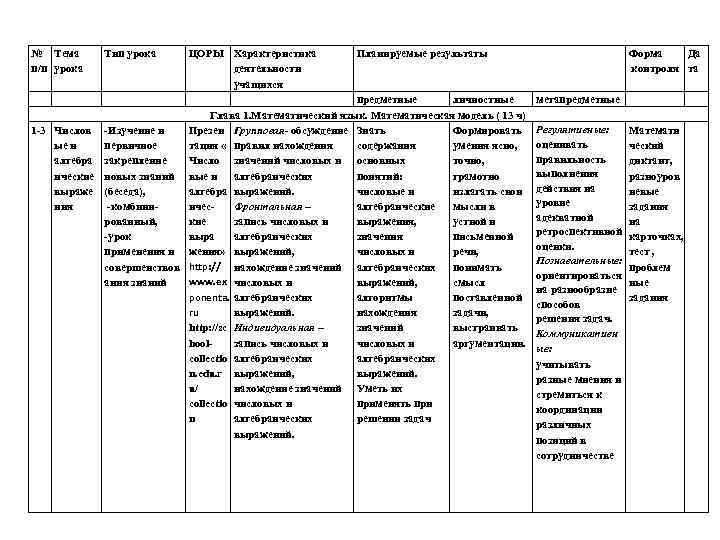№ Тема п/п урока Тип урока ЦОРЫ Характеристика деятельности учащихся Планируемые результаты предметные личностные Глава 1. Математический язык. Математическая модель ( 13 ч) 1 -3 Числов -Изучение и Презен Групповая- обсуждение Знать Формировать ые и первичное тация « правил нахождения содержания умения ясно, алгебра закрепление Число значений числовых и основных точно, ические новых знаний вые и алгебраических понятий: грамотно выраже (беседа), алгебра выражений. числовые и излагать свои ния -комбиниичес. Фронтальная – алгебраические мысли в рованный, кие запись числовых и выражения, устной и -урок выра алгебраических значения письменной применения и жения» выражений, числовых и речи, совершенствов http: // нахождение значений алгебраических понимать www. ex числовых и ания знаний выражений, смысл ponenta. алгебраических алгоритмы поставленной ru выражений. нахождения задачи, http: //sc Индивидуальная – значений выстраивать hoolзапись числовых и аргументации. collectio алгебраических n. edu. r выражений, выражений. u/ нахождение значений Уметь их collectio числовых и применять при n алгебраических решении задач выражений. Форма Да контроля та метапредметные Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Познавательные: ориентироваться на разнообразие способов решения задач. Коммуникативн ые: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве Математи ческий диктант, разноуров невые задания на карточках, тест , проблем ные задания

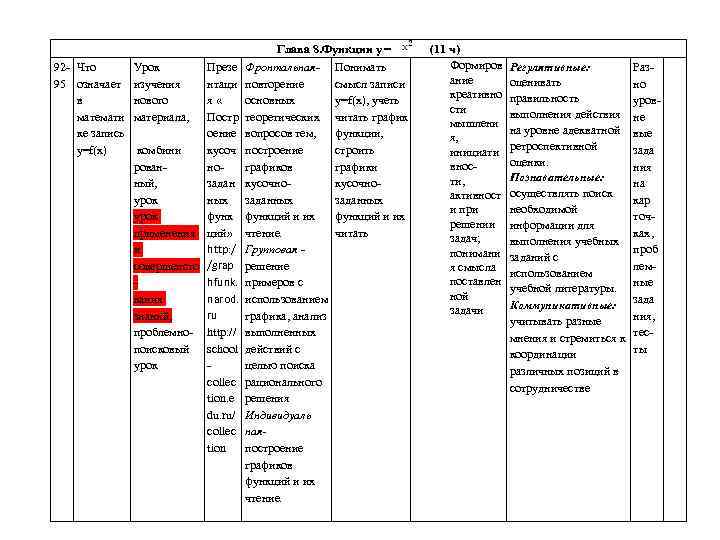92 - Что 95 означает в математи ке запись у=f(x) Урок изучения нового материала, Презе нтаци я « Постр оение кусоч комбини норованный, задан урок ных урок функ применения ций» http: / и совершенсто /grap hfunk. narod. вания ru знаний, проблемно- http: // поисковый school урок collec tion. e du. ru/ collec tion Глава 8. Функции у = (11 ч) Формиров Фронтальная- Понимать ание повторение смысл записи креативно основных у=f(x), учеть сти теоретических читать график мышлени вопросов тем, функции, я, построение строить инициати вносграфиков графики ти, кусочноактивност заданных и при функций и их решении чтение. читать задач; Групповая понимани решение я смысла поставлен примеров с ной использованием задачи графика, анализ выполненных действий с целью поиска рационального решения Индивидуаль наяпостроение графиков функций и их чтение. Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Познавательные: осуществлять поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве Разно уровне вые зада ния на кар точках, проб лемные зада ния, тесты

Формирование УУД на уроке алгебры в 7 классе Тема: Что означает в математике запись у=f(x) Урок № 3 Урок применения и совершенствования знаний

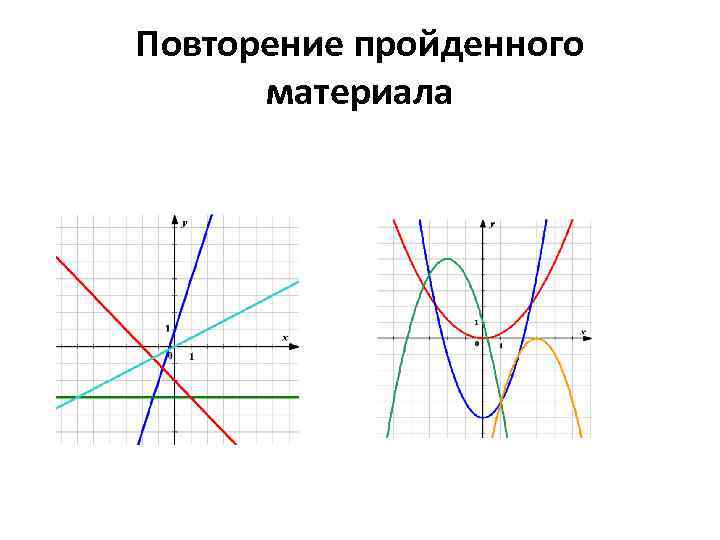Повторение пройденного материала

вида y = k х + b графиком функции является прямая 1. D( f ) = (- ; + ); 2. E( f ) = (- ; + ) • функция k>0 k=0 k<0

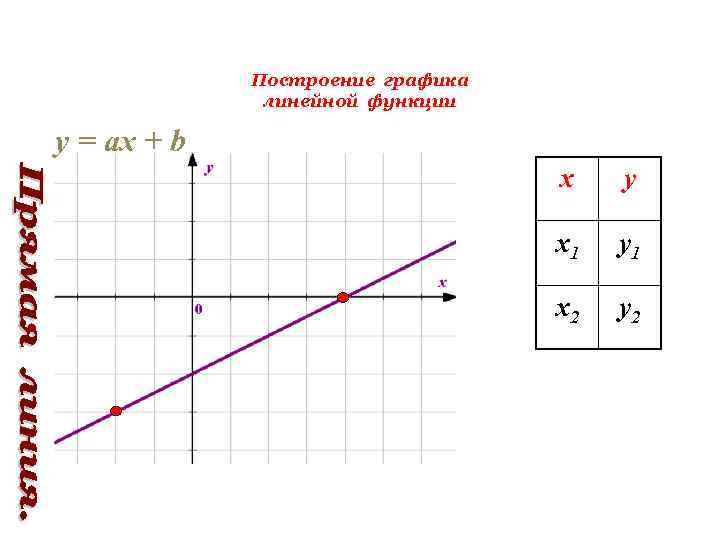Построение графика линейной функции y = ах + b х у х1 у1 х2 у2

№ 1. Повторение. Линейные функции. y = ах + b Верно!

№ 2. Повторение. Функции прямой пропорциональности. у = kx Правильно!

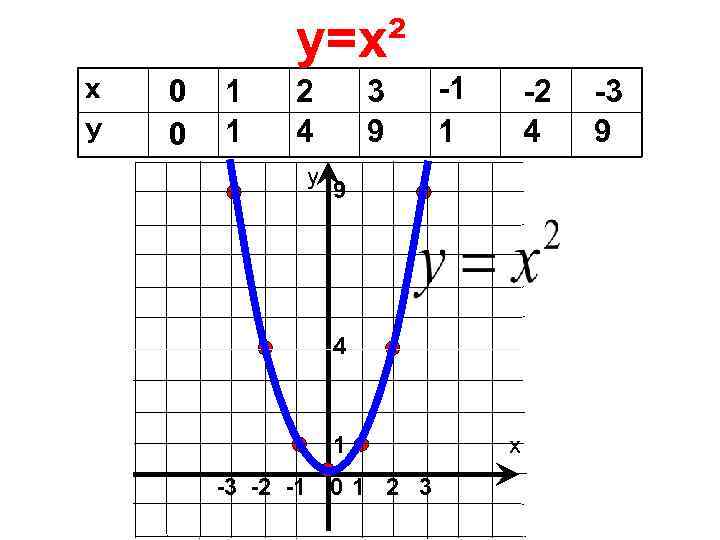у=х² х У 0 0 1 1 2 4 у 3 9 -1 1 -2 4 9 4 1 -3 -2 -1 0 1 2 3 х -3 9

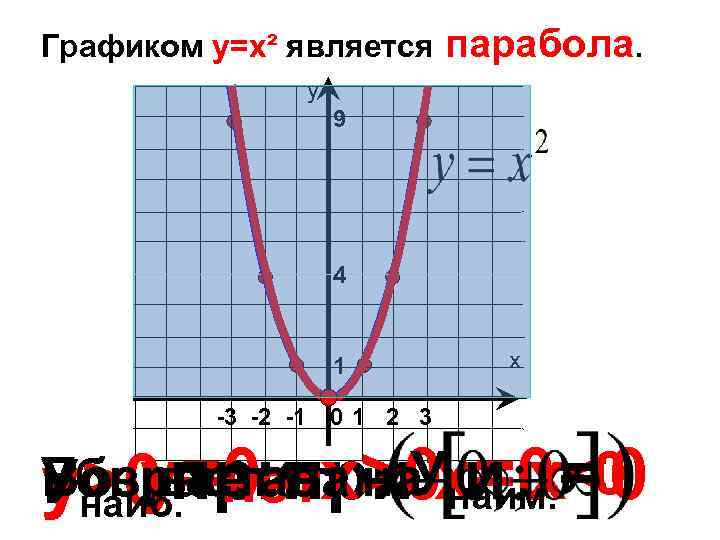Графиком у=х² является парабола. у 9 4 1 х -3 -2 -1 0 1 2 3 Возрастает на х=0 Убывает при. Унаим. =0 у=0 Унаиб. - нетх>0 и х<0 у>0 прина

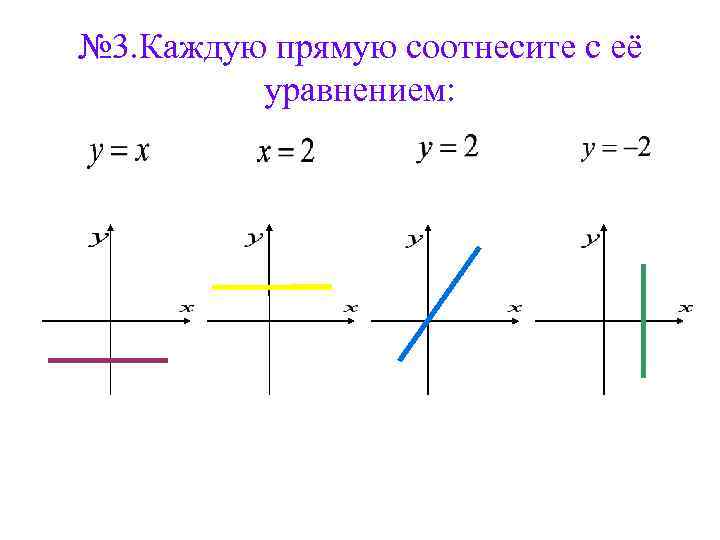№ 3. Каждую прямую соотнесите с её уравнением:

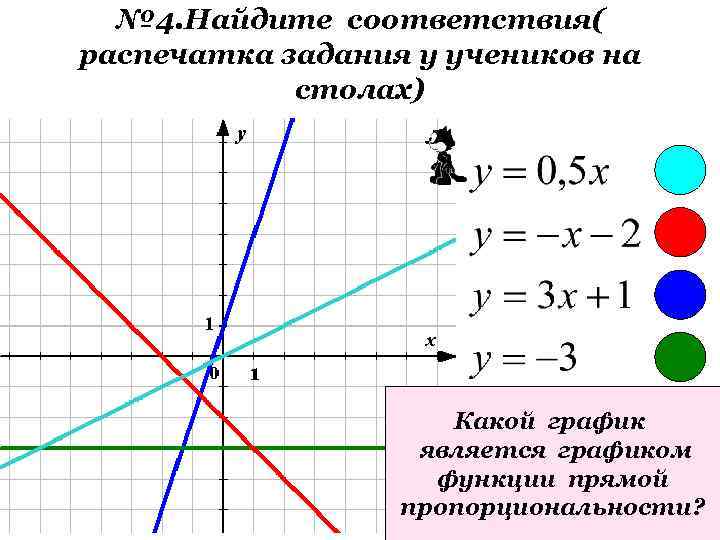№ 4. Найдите соответствия( распечатка задания у учеников на столах) Какой график является графиком функции прямой пропорциональности?

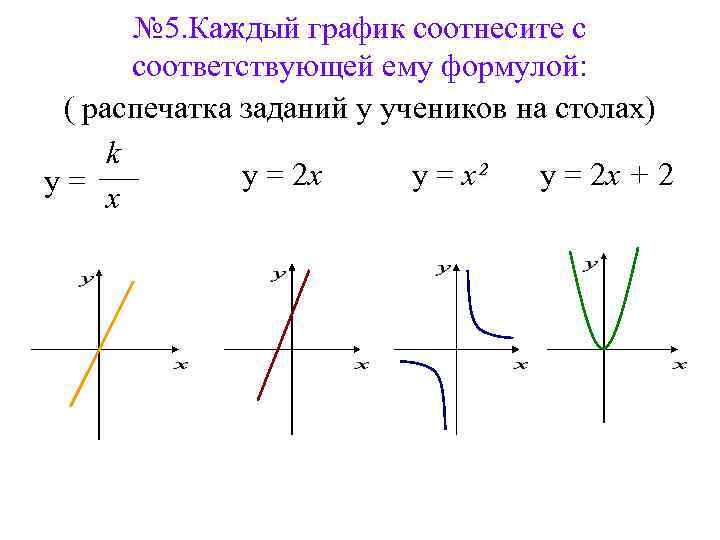№ 5. Каждый график соотнесите с соответствующей ему формулой: ( распечатка заданий у учеников на столах) k y = 2 x + 2 y = x² y= x

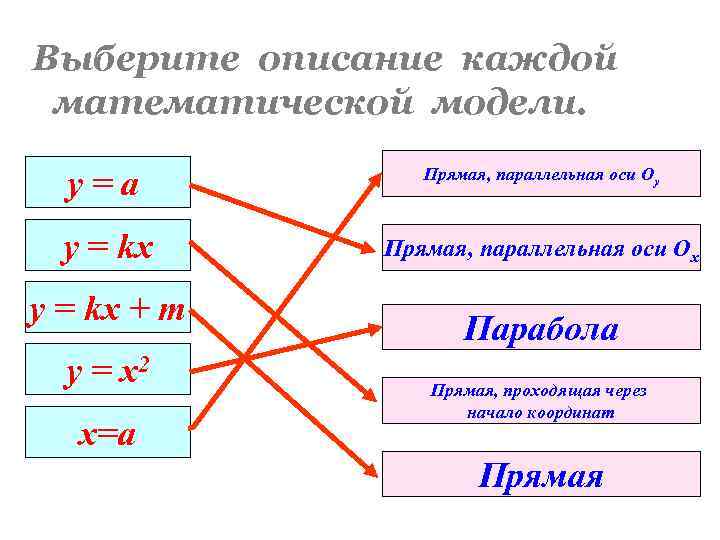Выберите описание каждой математической модели. у=а Прямая, параллельная оси Оу y = kx Прямая, параллельная оси Ох y = kx + m y = x 2 х=а Парабола Прямая, проходящая через начало координат Прямая

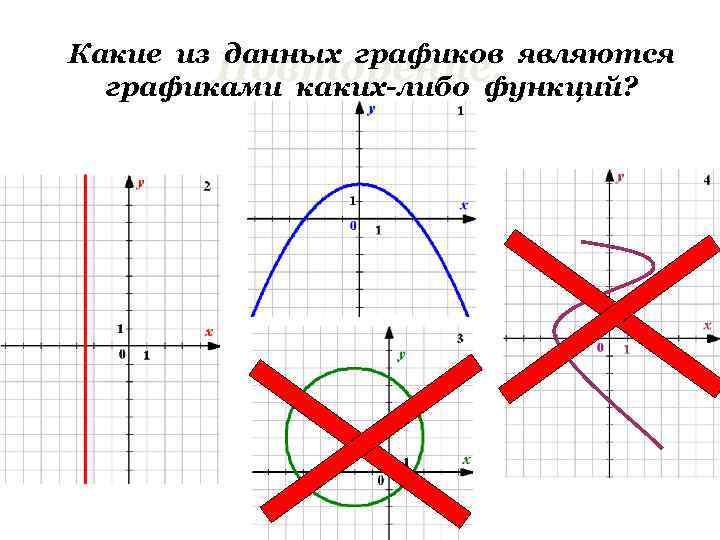Какие из данных графиков являются Повторение. графиками каких-либо функций?

Постройте график функции 2 x, если х<0 f(x)= х², если х≥ 0

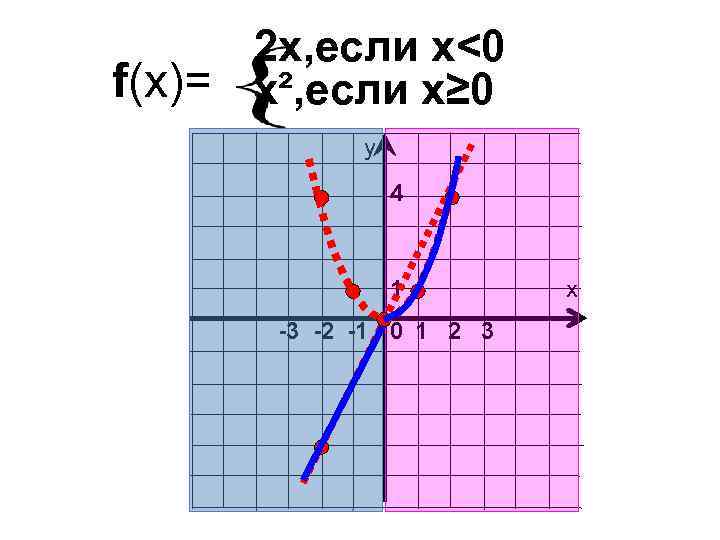2 x, если х<0 f(x)= х², если х≥ 0 у 4 1 -3 -2 -1 0 1 2 3 х

Самостоятельная работа № 6. Постройте графики функции • Вариант1 • Вариант2 • 1) у = 2 х-3 • 2) у = -1. 5 х+2 • 1) у= 3 х-2 • 2) у= -0. 5 х+1 • 3) • 4)

Оцените свою работу по следующим критериям: • Отметка « 5» - верно выполнены все задания; « 4» - верно выполнены задания № 1 -3; « 3» -верно выполнены любые 2 задания; « 2» - верно выполнены менее 2 заданий.

Постройте график уравнения ( осознание проблемы, постановка цели работы, переход к работе в группах)

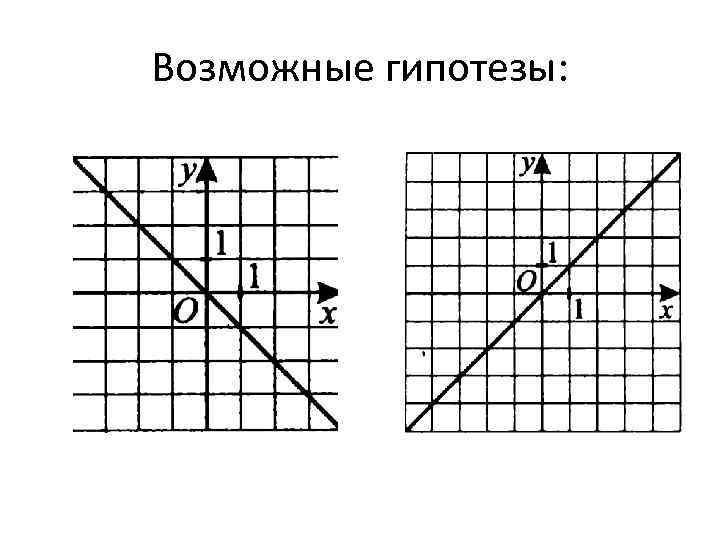Возможные гипотезы:

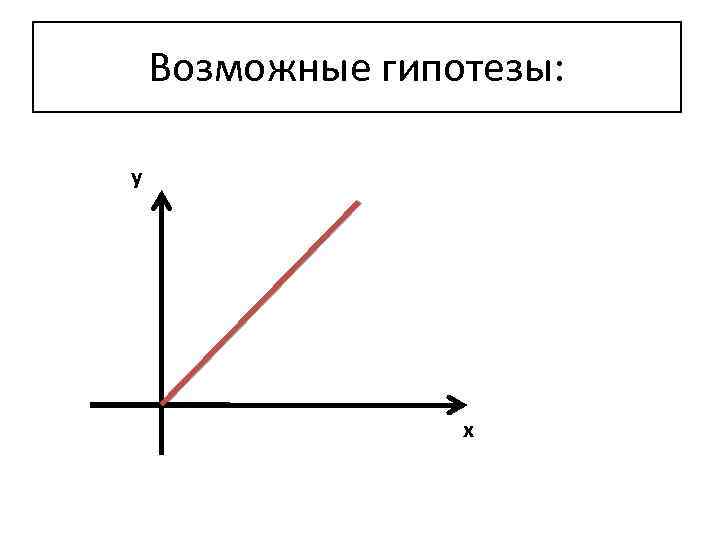Возможные гипотезы: у х

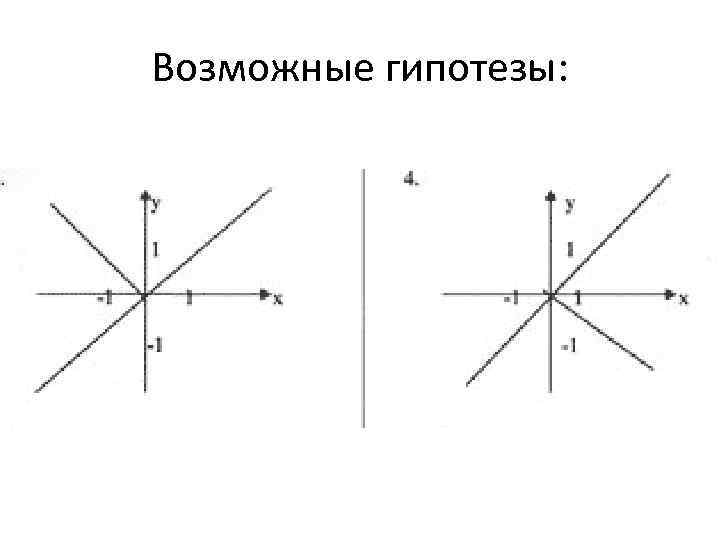Возможные гипотезы:

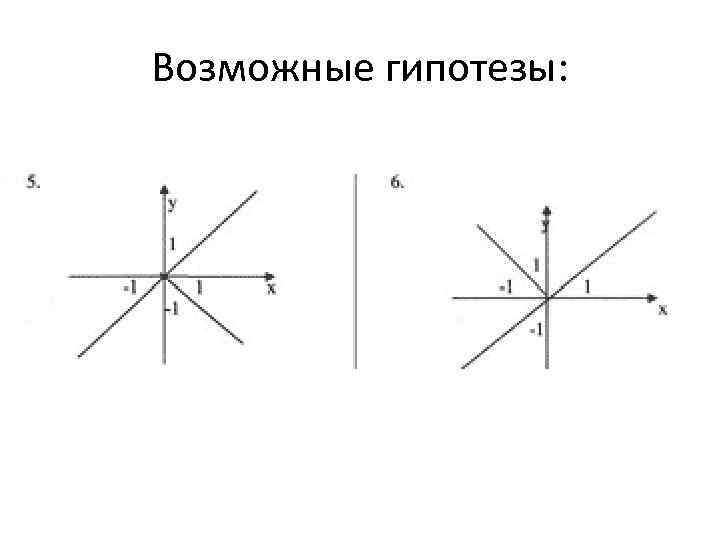Возможные гипотезы:

Обсуждение гипотез • Каждая группа по очереди защищает свою гипотезу, остальные ученики принимают участие в обсуждении.

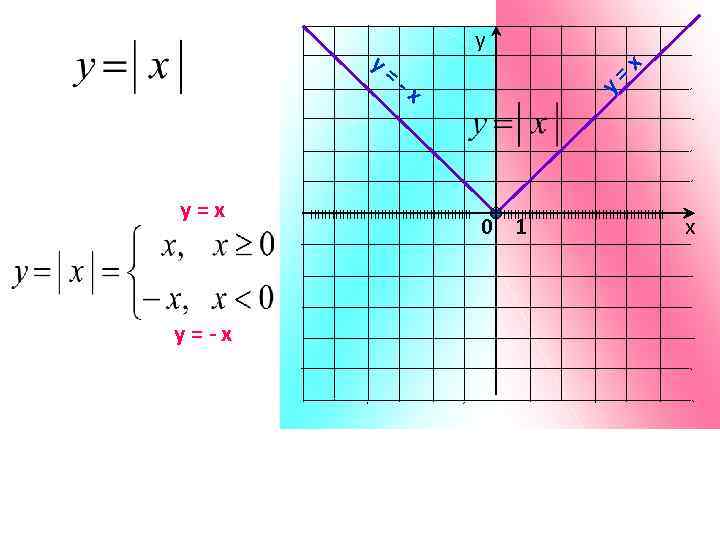у= у=х у=-х у х = у -х IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 0 1 х

Вывод по проделанной работе: Вопросы: 1)Как доказать , что график действительно график функции? -снять модуль и записать 2)Что является графиком функции? график функции на промежутке [0; ∞) совпадает с графиком функции у = х, а на промежутке (-∞; 0] – с графиком функции у = -х

Перечислите свойства функции ( работа в группах с последующей взаимопроверкой и фронтальной проверкой)

y = |x| • 1. D( f ) = (- ∞; + ∞) 2. E( f ) = [0; ∞); • 3. Функция убывает на луче • (- ∞; 0] , • возрастает на луче [0; + ∞) • 4. у= 0, при х=0; • 5. Унаим=0 при х=0, Унаиб- не существует; 6. Функция непрерывная

УУД • Познавательные: -устанавливать причинно- следственные связи; -давать определение понятиям; -осуществлять сравнение, самостоятельно выбирая основания для указанной операции; -строить логические рассуждения, включающее установление причинно- следственных связей. Получит возможность научиться: - ставить проблему, - выдвигать гипотезу о связях объектов; - самостоятельно проводить исследование на основе применения методов наблюдения; - делать выводы на основе аргументации.

УУД • регулятивные : - принимать решения в проблемной ситуации на основе переговоров; -адекватно самостоятельно оценивать правильность выполнения действия и вносить необходимые коррективы в исполнение как в конце действия , так и по ходу его реализации Получит возможность научиться: -адекватно оценивать свои возможности достижения цели; -основам саморегуляции в познавательной деятельности в форме осознанного управления своим поведение и деятельностью, направленной на достижение поставленной цели.

УУД • Коммуникативные: -учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве; -формулировать собственное мнение, аргументировать и координировать его с мнениями партнеров в сотрудничестве при выборе общего решения в совместной деятельности; -аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для опонентов способом. - Получит возможность научиться: -брать на себя инициативу в организации совместного действия; -учитывать разные мнения.

УУД • Личностные: -умение вести диалог на основе равноправных отношений и взаимного уважения, доброжелательное отношение к окружающим. - Получит возможность для формирования: -устойчивого следования в поведении этическим требованиям

Отчет по работе над проектом

Цель работы: 1. Показать, что понимание человечеством функциональных связей и взаимосвязей между отдельными качествами жизни(добро, зло, богатство, бедность, …)послужило источником происхождения многих пословиц и поговорок, без которых наша речь была бы невыразительной и обыденной. 2. Показать, что понятие “функция” находит широкое применение в жизни.

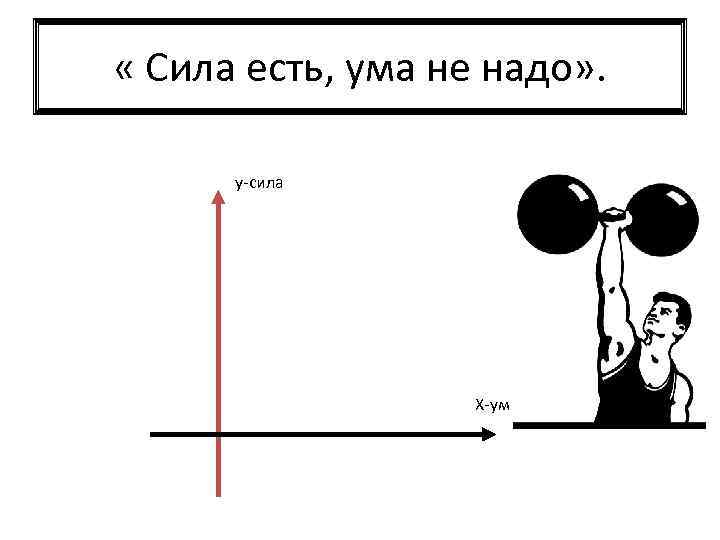« Сила есть, ума не надо» . у-сила Х-ум

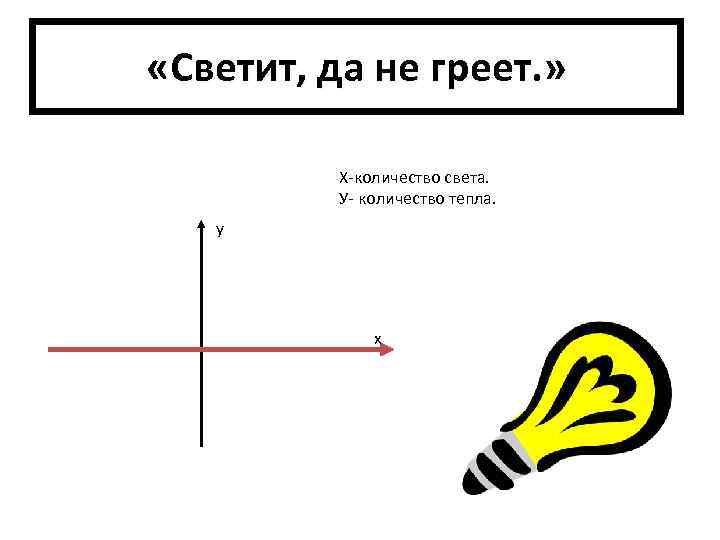«Светит, да не греет. » Х-количество света. У- количество тепла. y x

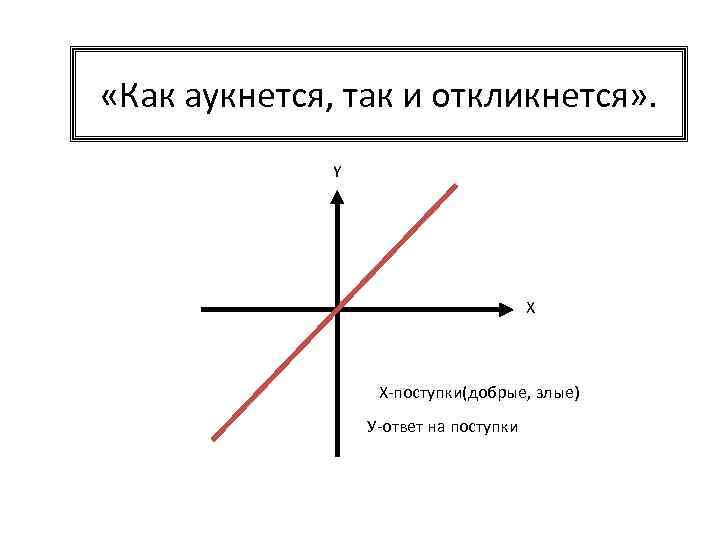«Как аукнется, так и откликнется» . Y X Х-поступки(добрые, злые) У-ответ на поступки

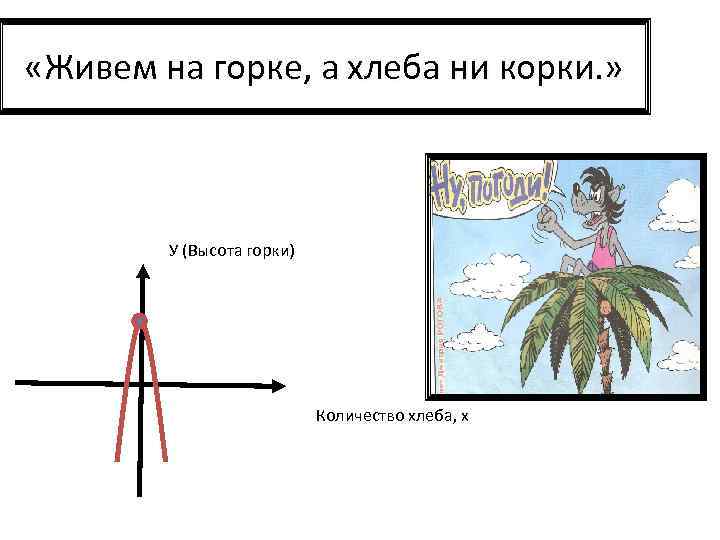«Живем на горке, а хлеба ни корки. » У (Высота горки) Количество хлеба, x

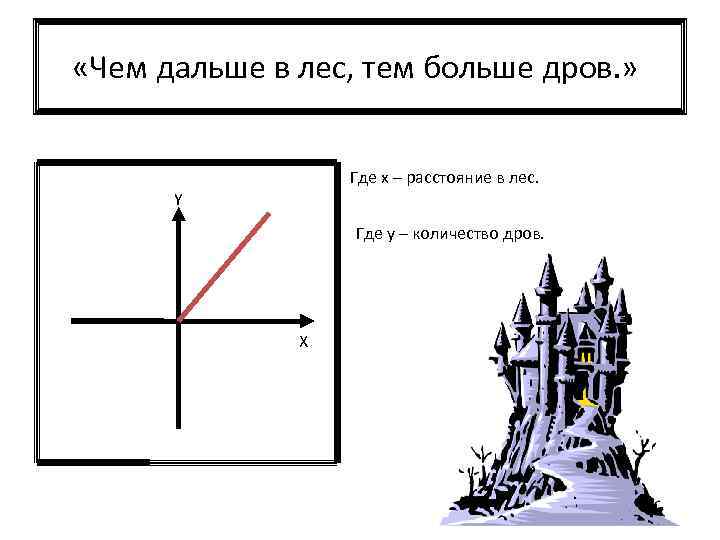«Чем дальше в лес, тем больше дров. » Где х – расстояние в лес. Y Где у – количество дров. X

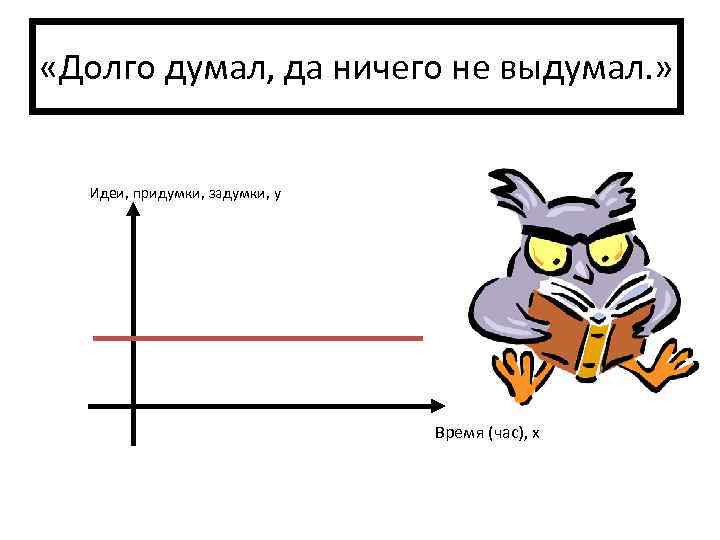«Долго думал, да ничего не выдумал. » Идеи, придумки, задумки, y Время (час), x

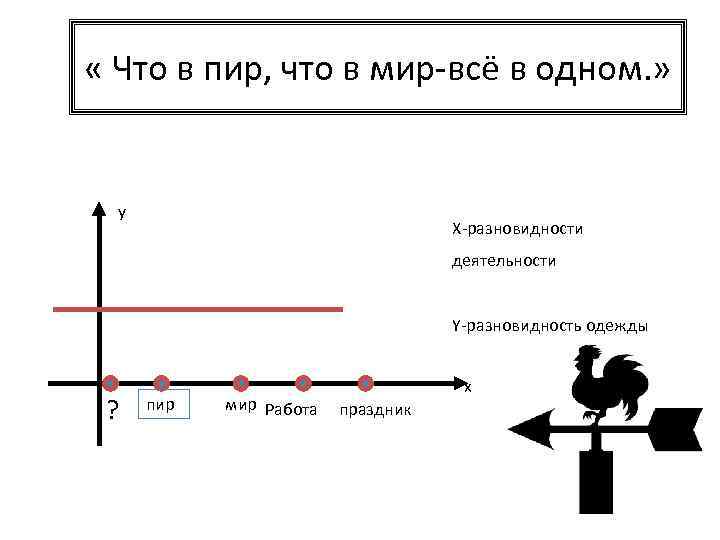« Что в пир, что в мир-всё в одном. » у Х-разновидности деятельности Y-разновидность одежды ? пир мир Работа х праздник

« Кто любит трудиться, тому есть чем гордиться. » гордость труд

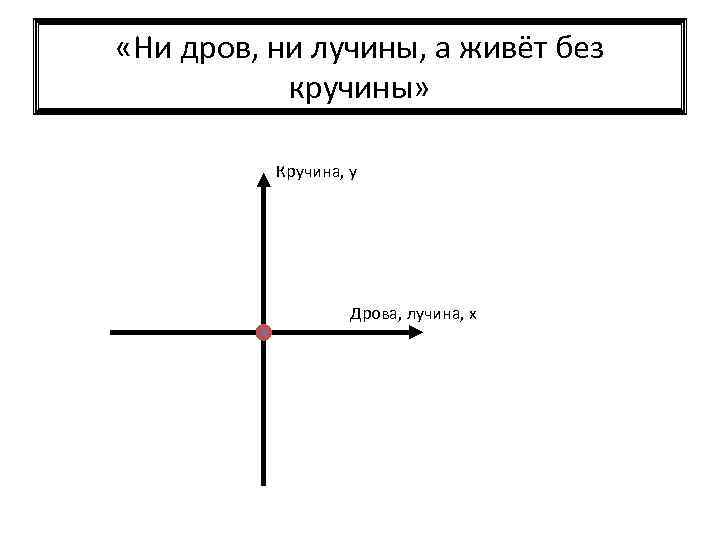«Ни дров, ни лучины, а живёт без кручины» Кручина, y Дрова, лучина, x

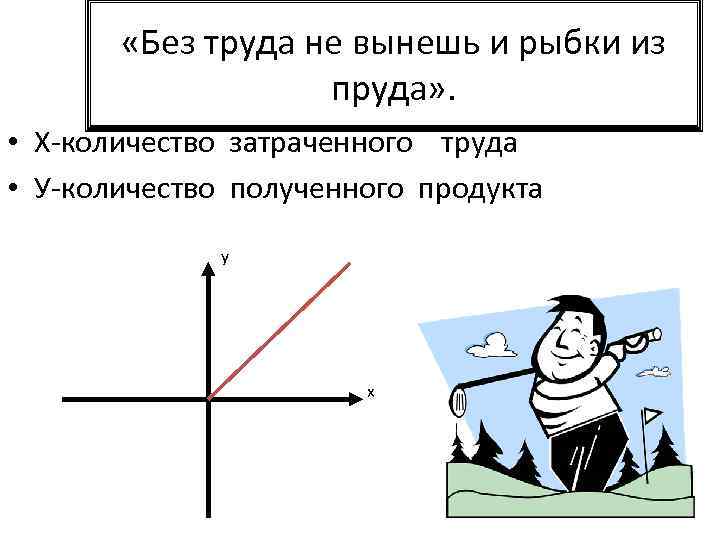«Без труда не вынешь и рыбки из пруда» . • Х-количество затраченного труда • У-количество полученного продукта у х

Спасибо за внимание!