Real-Time Signalextraction MDFA and Algorithmic Trading marc wildi zhaw

Real-Time Signalextraction (MDFA) and Algorithmic Trading marc. wildi@zhaw. ch http: //blog. zhaw. ch/idp/sefblog http: //www. idp. zhaw. ch/usri http: //www. idp. zhaw. ch/MDFA-XT http: //www. idp. zhaw. ch/sef

Background • Hybrid math/econ. • IDP-ZHAW → Projects with econ. partners • Forecasting – Health-care (cost expenditures) – Macro (real-time economic indicators: EURI Eurostatproject) – Finance (MDFA-XT, large hedge-fund) – Engineering (Telecom, load forecasts) • Eclectic/disparate range of applications • Common methodological approach(es) – In-house developments: (M)DFA – R-package “signalextraction” on CRAN

A Classical Algorithmic Trading Approach Timing System SP 500 Daily Closures MA(200), Equally Weighted

P. 5 (drawdowns), p. 7 (timing system), p. 10 (performance)

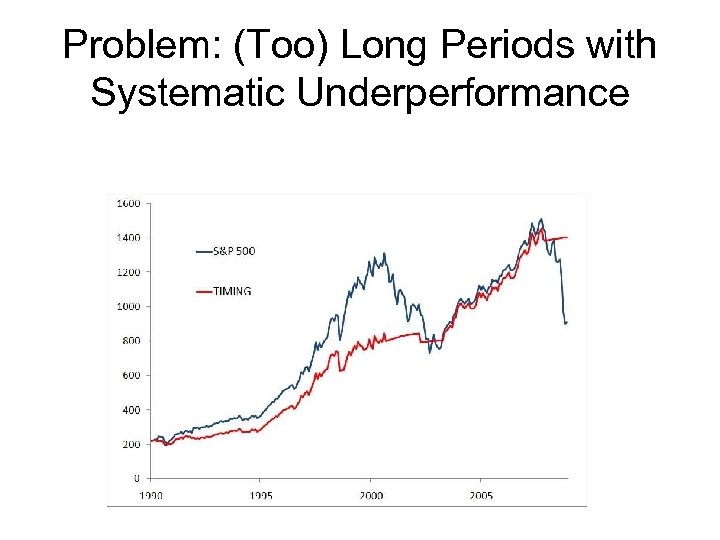Problem: (Too) Long Periods with Systematic Underperformance

Why do Traders Frequently Adopt/Prefer Filter Crossings? Filter Characteristics Why MDFA? http: //blog. zhaw. ch/idp/sefblog/index. php? /archives/54 Intermezzo-Why-do-Traders-Often-Consider-Crossings-of. Trading-Filter-Pairs. html

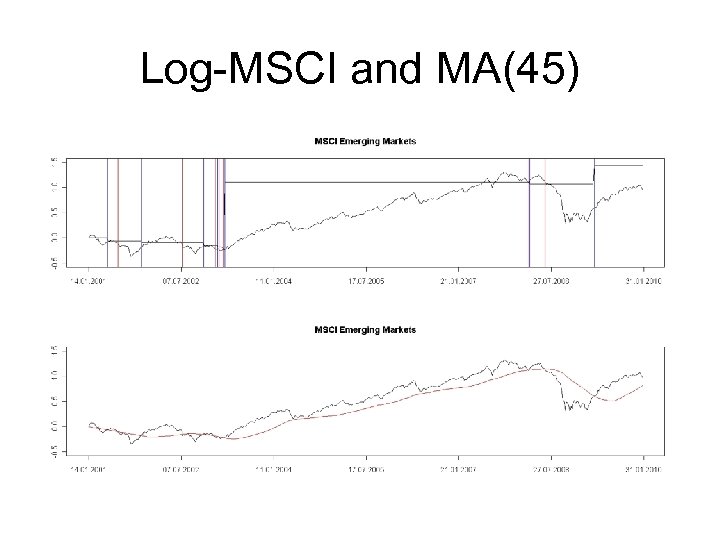Log-MSCI and MA(45)

Filter Characteristics • Amplitude function: – Which signal is extracted? • Time-shift: – How large is the delay?

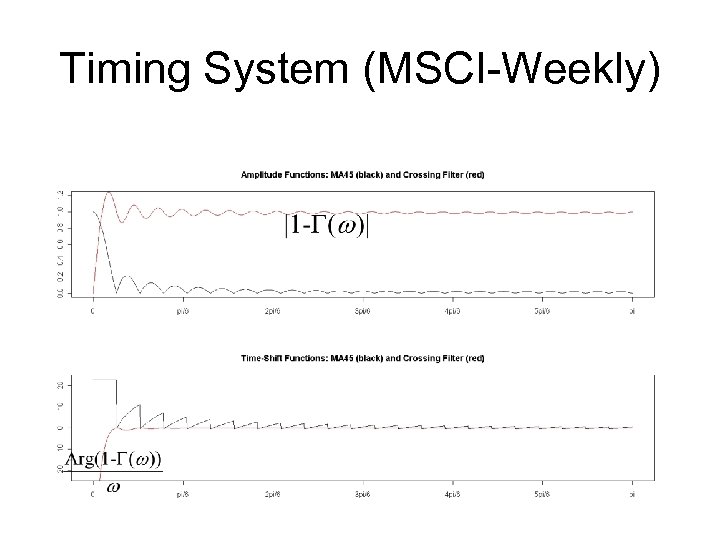Timing System (MSCI-Weekly)

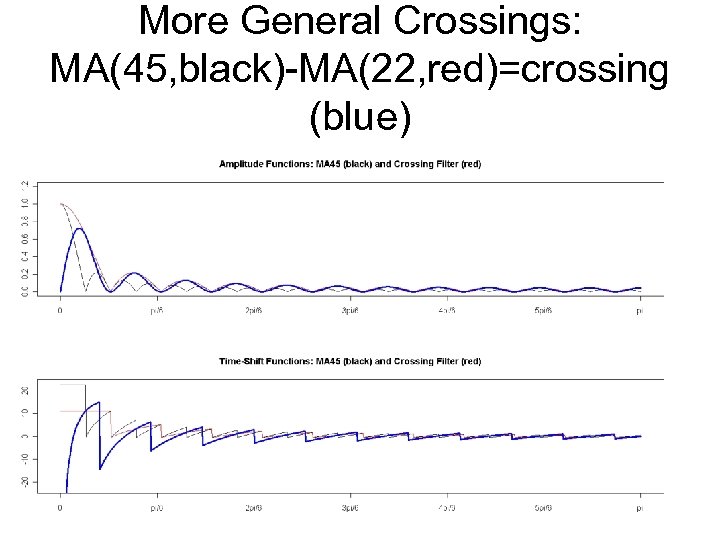More General Crossings: MA(45, black)-MA(22, red)=crossing (blue)

Conclusions • Crossing-rules are (an unnecessarily cumbersome way of implementing) bandpass filters • Crossing-rules (bandpass) have small time delays • Why MDFA? – Flexible efficient real-time (bandpass) design – Fast and smooth

Fundamental Trading http: //www. idp. zhaw. ch/usri SP 500 http: //blog. zhaw. ch/idp/sefblog

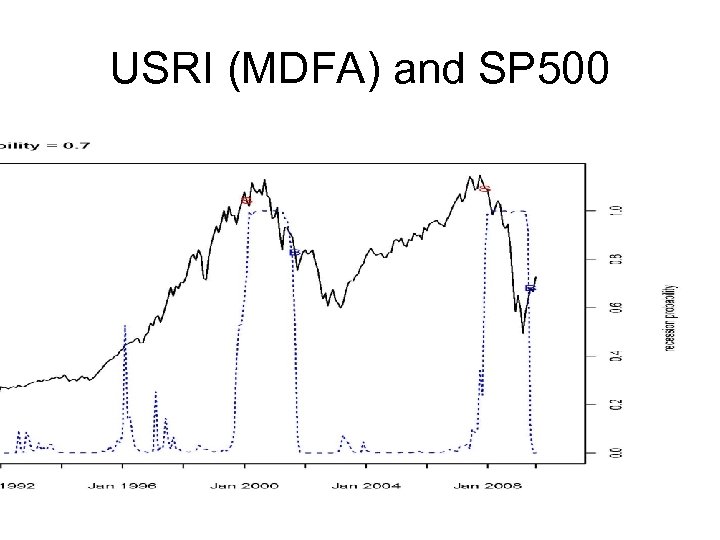USRI (MDFA) and SP 500

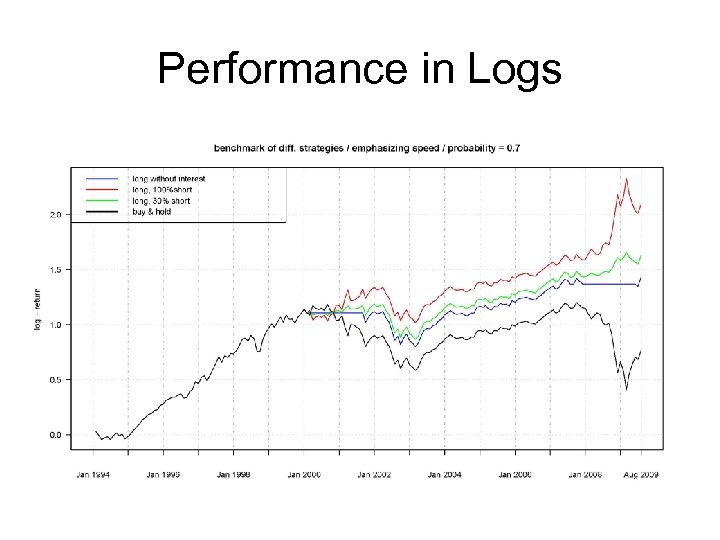Performance in Logs

Student Thesis p. 19 Long Term Performances Fundam. Trading

Conclusion • Damp or avoid all massive recession draw -downs effectively – Ideal for risk-averse investors (pension funds) • Fundamental Trading: truly out of sample – Focus on Macro-data (finance data ignored) – NBER • Disadvantage: `insufficiently active’ – Texto: «Difficult to justify fees»

MDFA-XT http: //www. idp. zhaw. ch/MDFA-XT MSCI (+BRIC) http: //blog. zhaw. ch/idp/sefblog

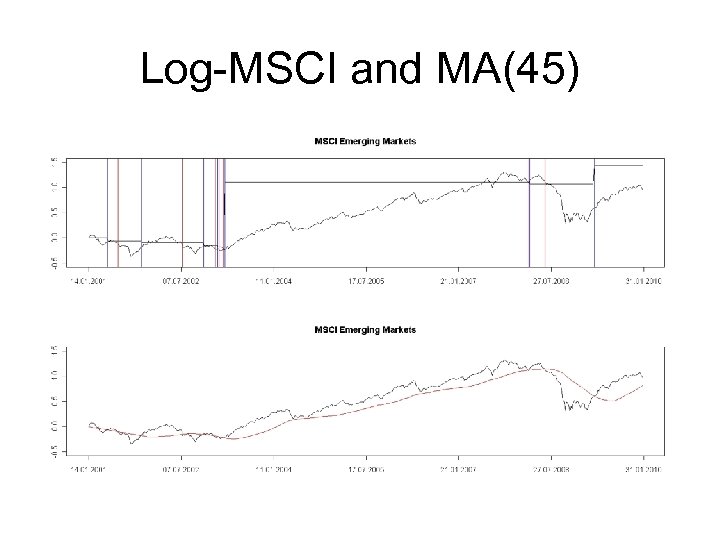Log-MSCI and MA(45)

MDFA vs. MA(45) weekly data MDFA (blue) Faster

Five Trading Filters Different Trading Frequencies

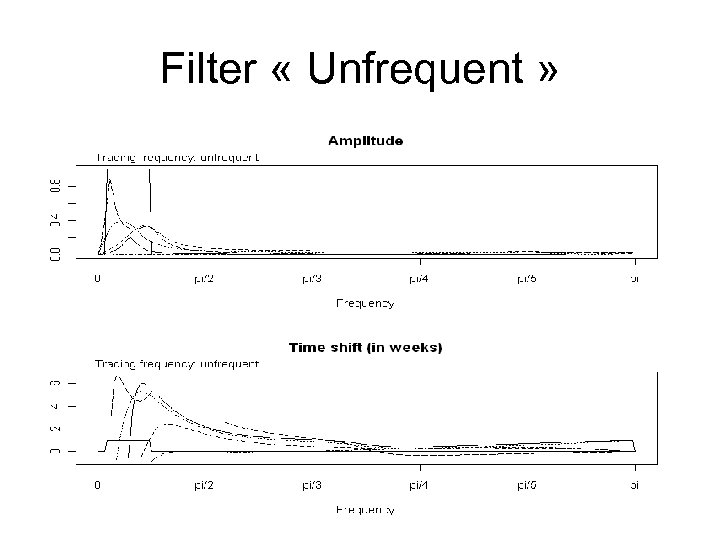Filter « Unfrequent »

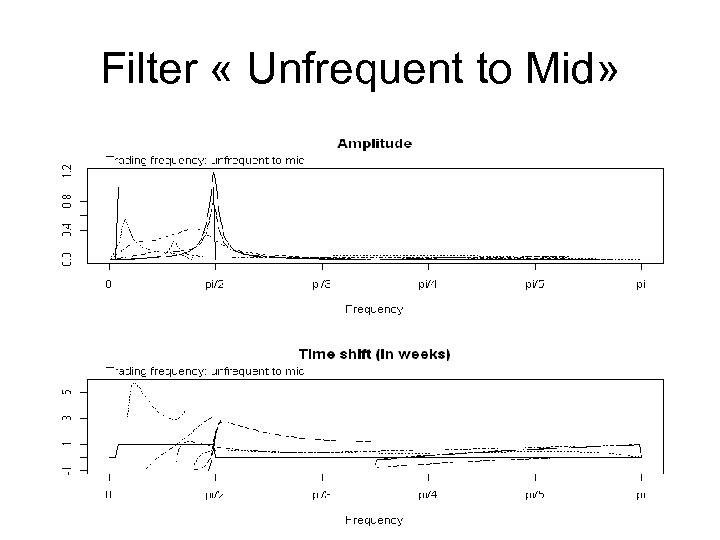Filter « Unfrequent to Mid»

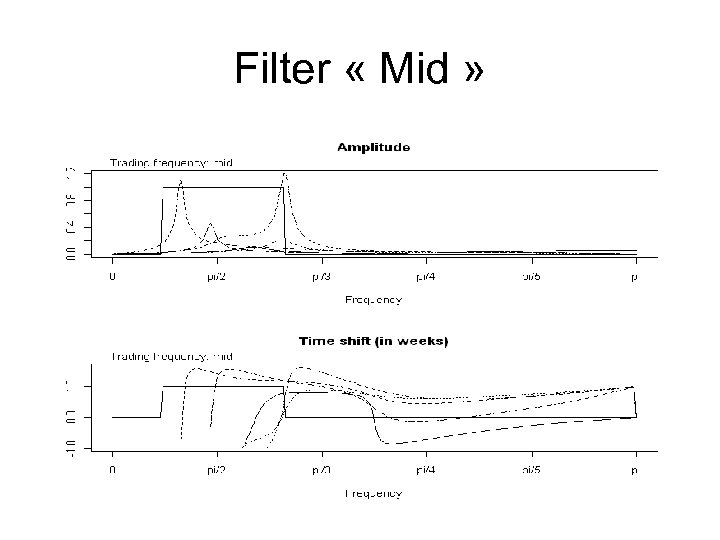Filter « Mid »

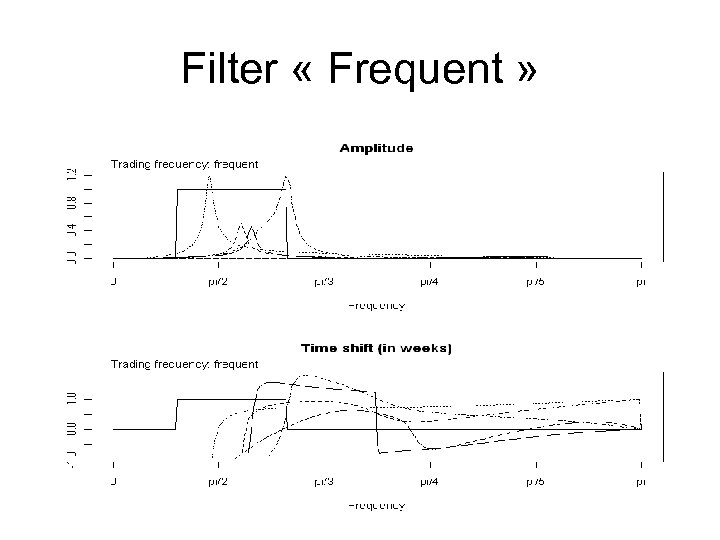Filter « Frequent »

Conclusion • Higher trading frequencies are associated with – Bandpass shifted to the right • More flexible than traditional filter-crossings – Smaller delays/time shifts

Performances

Setting • Total degenerative trading costs of 0. 3% per order (small fund) • Long only • No risk free interest rates

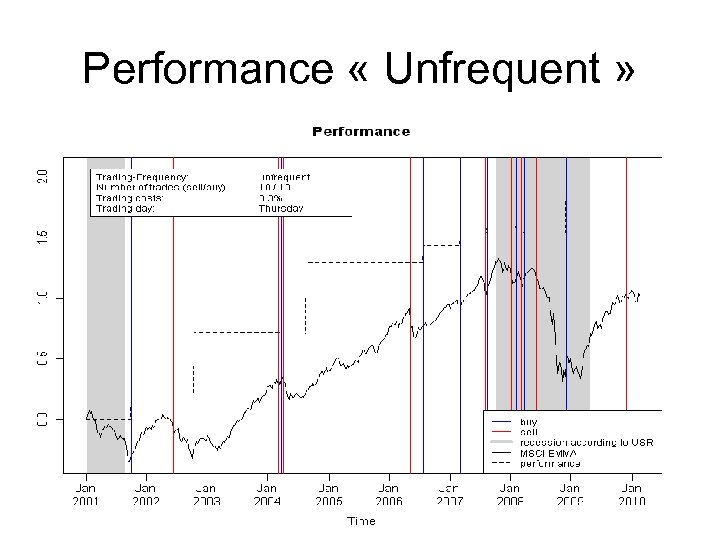Performance « Unfrequent »

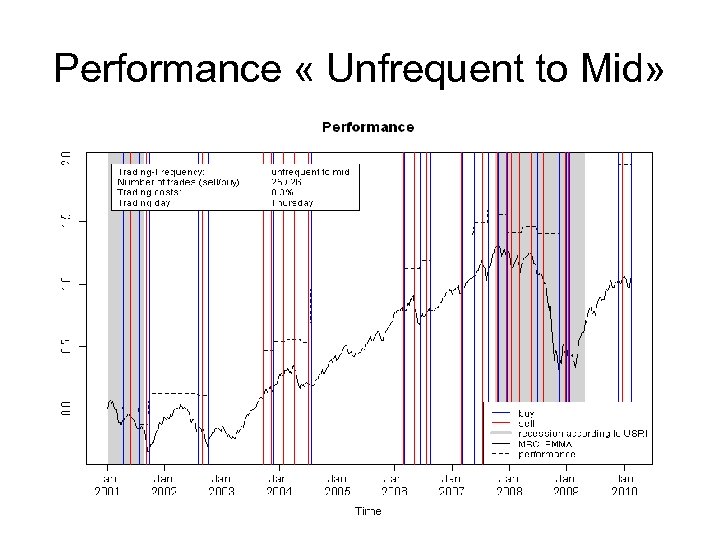Performance « Unfrequent to Mid»

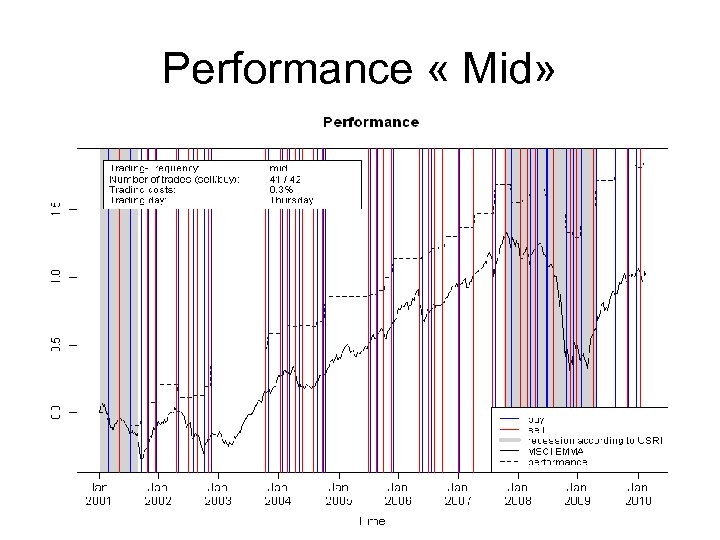Performance « Mid»

Performance « Mid to Frequent »

Performance « Frequent »

Conclusions • Higher trading frequencies are associated with – Slight reduction of performance – Larger draw-downs • USRI would avoid draw-downs and then the performance would improve – Increased market activity (fees!) • Combination with USRI possible (recommended) • Filters will be available on-line in late July

Real-Time Signalextraction A SEF-Blog Excel-Tutorial http: //blog. zhaw. ch/idp/sefblog

Excel-Tutorial on SEF-Blog • http: //blog. zhaw. ch/idp/sefblog/index. php? / archives/65 -Real-Time-Detection-of. Turning-Points-a-Tutorial-Part-I-Mean. Square-Error-Norm. html • http: //blog. zhaw. ch/idp/sefblog/index. php? / archives/67 -Real-Time-Detection-of. Turning-Points-a-Tutorial-Part-IIEmphasizing-Turning-Points. html

Purposes • Yoga exercises to detach from main-stream maximum likelihood world • First Blog-entry: how traditional econometric approach `works’ – Intuitively straightforward – Good (optimal) mean-square performances – People have become lazy-minded • Second Blog-Entry: the early detection of turning points – Is a (strongly) counterintuitive exercise – Generates seemingly (strongly) misspecified filter designs • Warning → Learning (→ Illumination? )

Excel-Tutorial on SEF-Blog

Real-Time Signalextraction 1. Traditional Econometrics

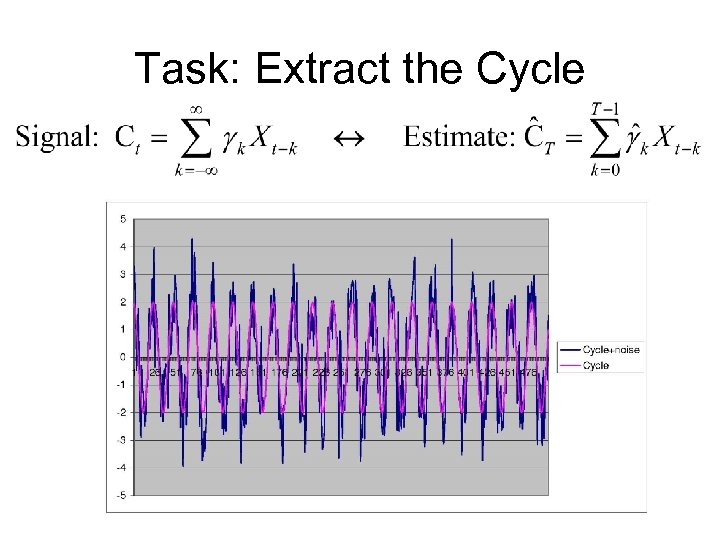Task: Extract the Cycle

Standard Econometric Approach • Proceeding: – Identify a time-series model (ARIMA/state space) – Extend the series by optimal forecasts – Apply the symmetric filter on the extended time series • X-12 -ARIMA, TRAMO, STAMP, R/S+… • Claim: – One-sided filter is optimal (mean-square sense) – Assumption: DGP/true model

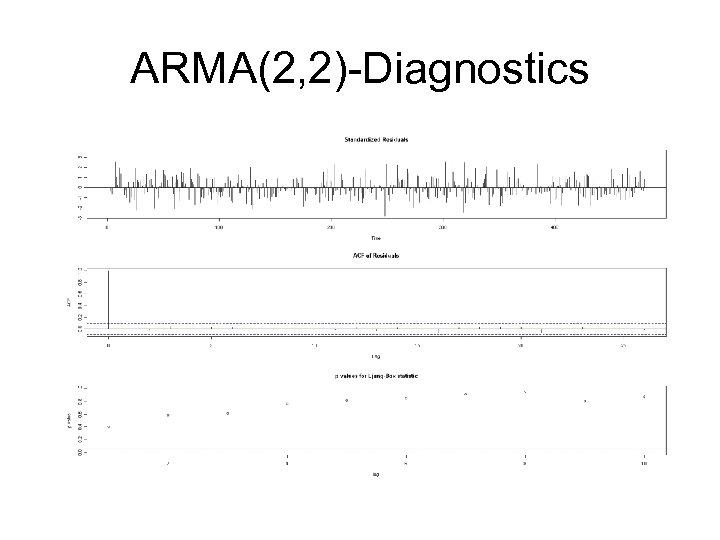ARMA(2, 2)-Diagnostics

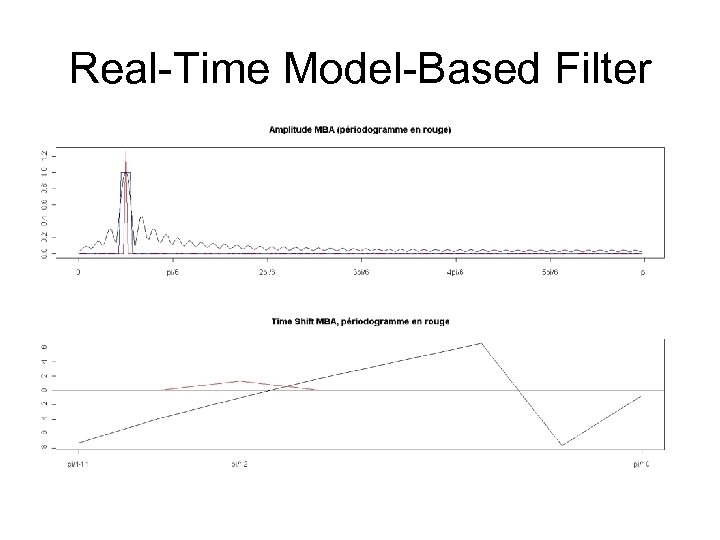Real-Time Model-Based Filter

Real-Time Signalextraction 2. Excel Example (Replication of Model-Based Approach)

Parameters (ARMA(2, 2)-FILTER) • ARMA(2, 2)-Filter (not model)

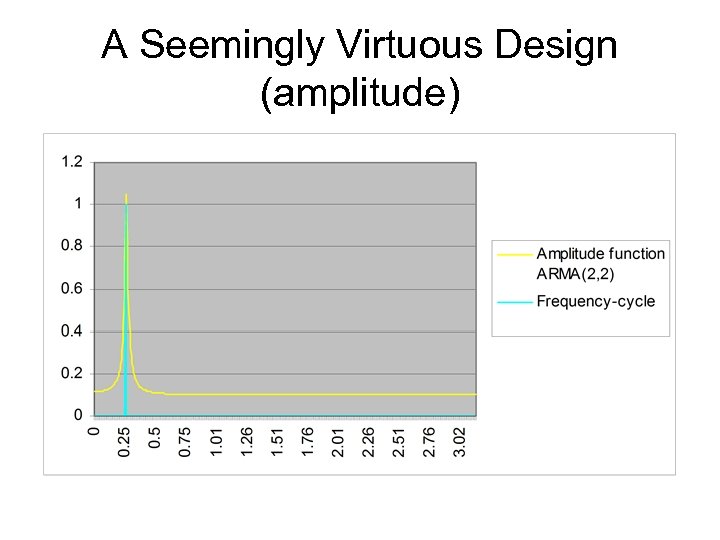A Seemingly Virtuous Design (amplitude)

A Seemingly Virtuous Design (time shift)

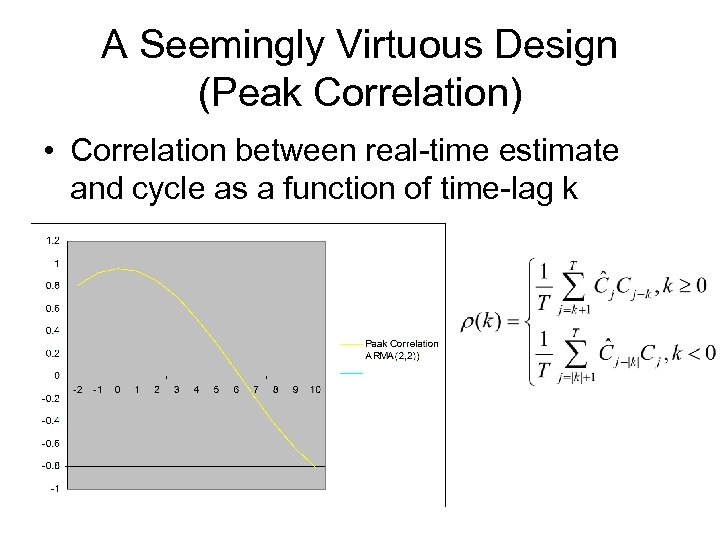A Seemingly Virtuous Design (Peak Correlation) • Correlation between real-time estimate and cycle as a function of time-lag k

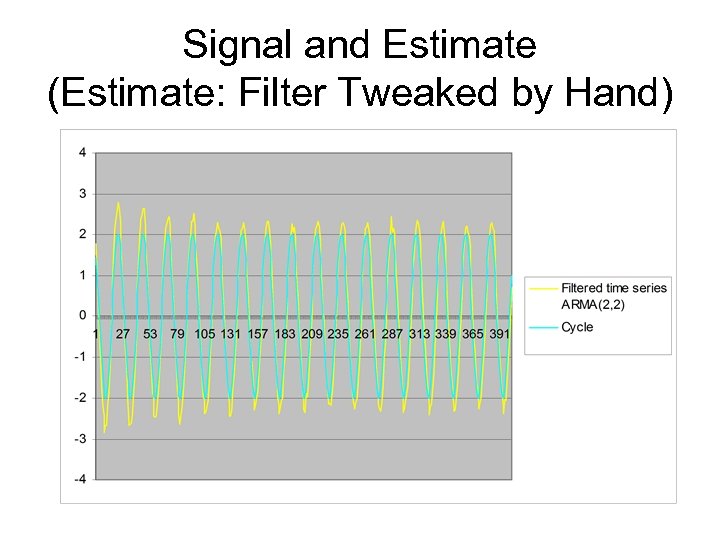Signal and Estimate (Estimate: Filter Tweaked by Hand)

Real-Time Signalextraction 3. Excel Example (Turning Point Revelation)

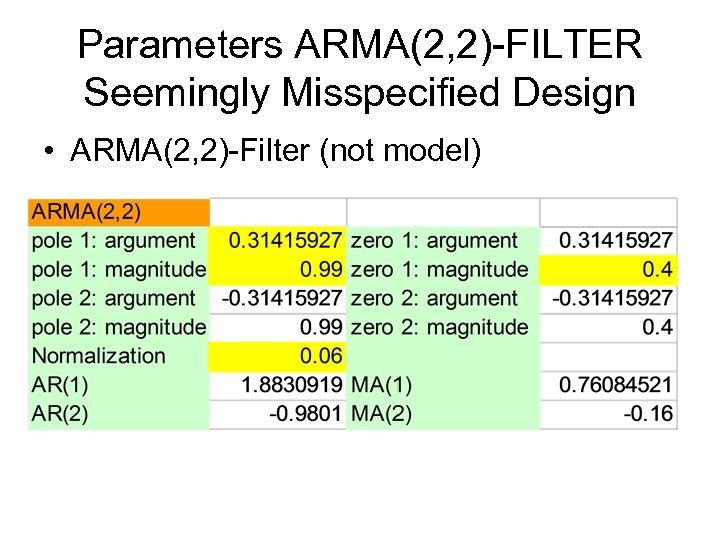Parameters ARMA(2, 2)-FILTER Seemingly Misspecified Design • ARMA(2, 2)-Filter (not model)

A Seemingly Misspecified Design Amplitude

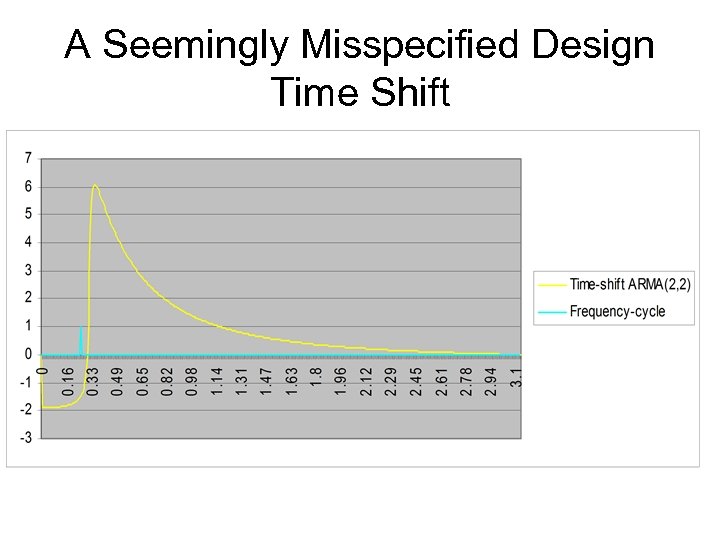A Seemingly Misspecified Design Time Shift

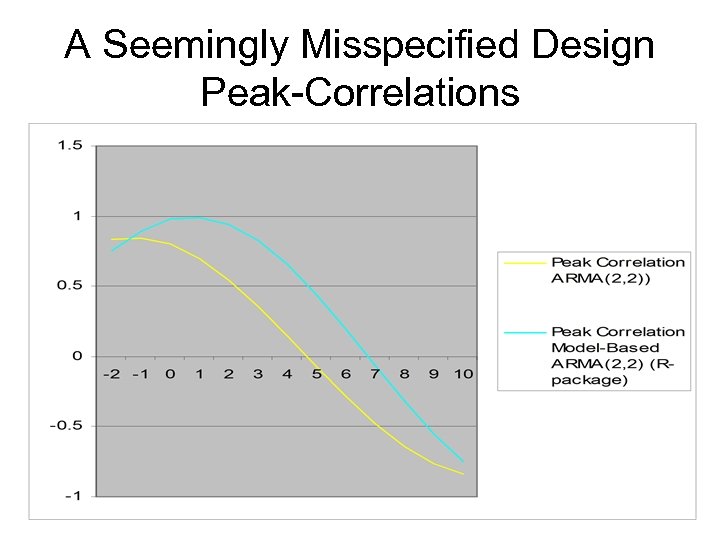A Seemingly Misspecified Design Peak-Correlations

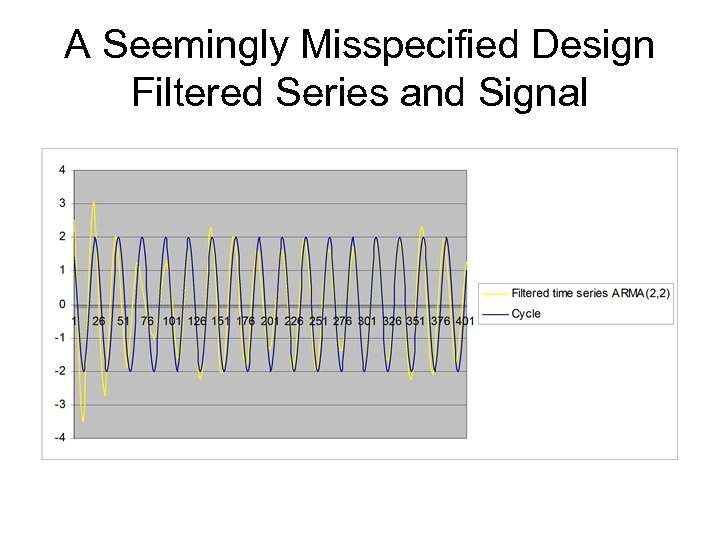A Seemingly Misspecified Design Filtered Series and Signal

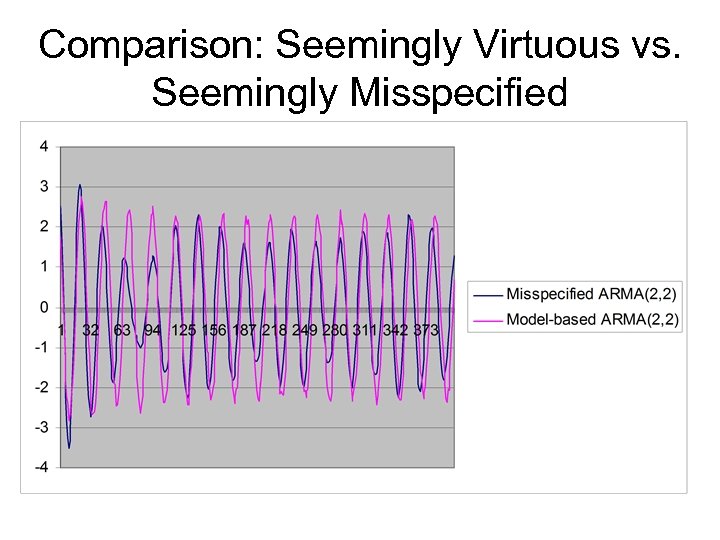Comparison: Seemingly Virtuous vs. Seemingly Misspecified

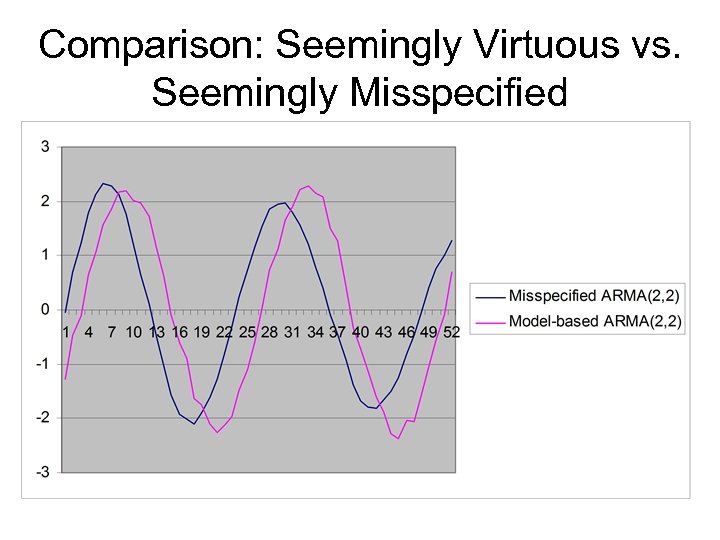Comparison: Seemingly Virtuous vs. Seemingly Misspecified

Conclusions • Seemingly misspecified design is – Faster – Smoother (less false TP’s or “alarms”) – Not mean-square optimal – Much better in a TP-perspective

From Excel to MDFA • Tweak filter parameters `by hand’ in Excel Tutorial • Shortcomings of example – Unrealistically simple artificial simulation exercise – In practice: • more complex nuisances and/or signals – Include information from more than one time series (multivariate framework) • Wish: a formal optimization criterion • Welcome to DFA and MDFA

DFA Direct Filter Approach Mean-Square

DFA: Direct Filter Approach • Idea: estimate mean-square filter error efficiently

Optimization Criterion (I(0)) • Minimize a (uniformly) superconsistent estimate of an (uniformly) efficient estimate of the filter mean-square error • (Customized) Efficiency enters explicitly in the Design of the Optimization Criterion

Did You Say and/or Mean “Periodogram”? • Periodogram is a typical example of “statisticbashing” – Inconsistent estimate of spectral density – Smoothing (parametric or non-parametric) • Periodogram has wonderful statistical properties – Sufficiency (Larry Brethorst) – One can derive nice formal efficiency results in realtime signalextraction • Working on a series of new Blog entries about the topic to rehabilitate – to some extent … - the periodogram

Performances (Efficiency of Univariate DFA) • Business Survey Data (KOF, FED, 2004, 2005) – X-12 -ARIMA, Tramo/Seats – MSE-gain ~30% • US- and Euro-GDP (2008): – CF – turning-points anticipated by 1 -2 quarters • ESI (2006): – Dainties – TP‘s discovered 2 -3 months earlier

Performances (Efficiency) by Relying on the Periodogram • TP-filters won NN 3 (2007) and NN 5 (2008) forecasting competitions (~60 participants) – IIF and University of Lancaster – Monthly Macro- and Financial Data (111 time series) and daily financial data (111 time series) – Outperformed winner and runner-up of prestigious M 3 competition, X-12 -ARIMA, Tramo, Forecast-Pro, Autobox, Exponential smoothing: Simple, Holt, Damped, … – Neural nets, artificial intelligence – http: //blog. zhaw. ch/idp/sefblog

DFA Direct Filter Approach Turning Points (TP)

Controlling the Time Delay (Customization) • λ>1: emphasize the time delay in the pass-band • λ=1: best level filter

Customization: Controlling time delay and smoothness • Stronger damping of highfrequency noise in stop-band • Smaller time delays in pass-band • W(ω) is monotonic (increasing) and λ>1

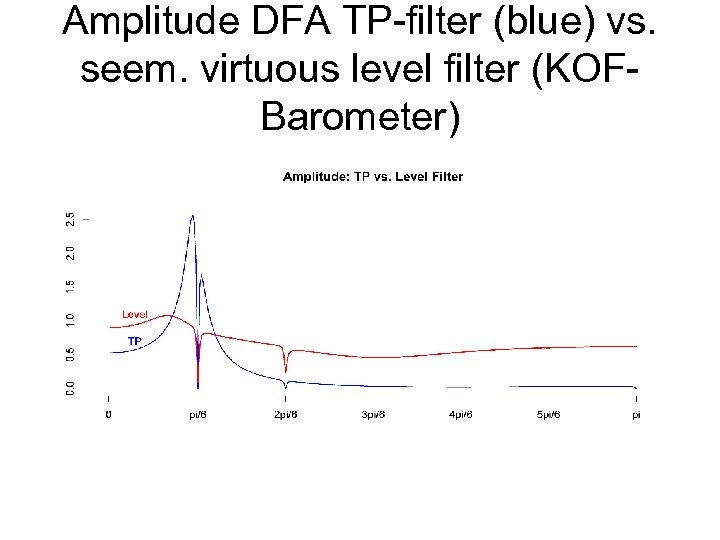Amplitude DFA TP-filter (blue) vs. seem. virtuous level filter (KOFBarometer)

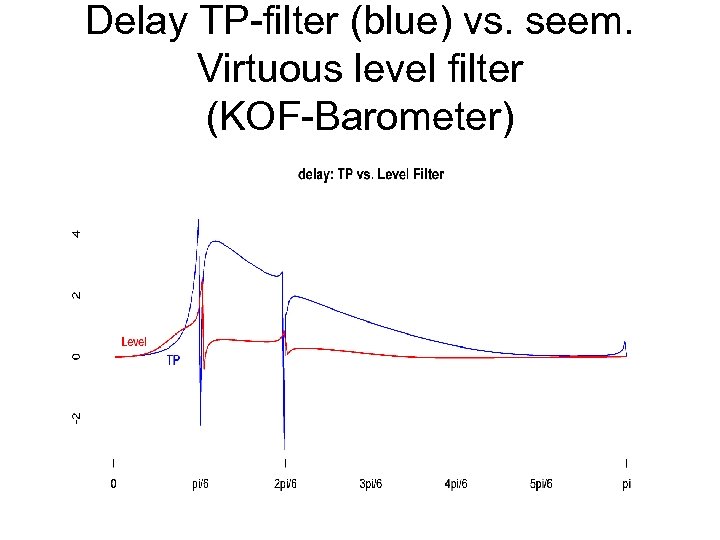Delay TP-filter (blue) vs. seem. Virtuous level filter (KOF-Barometer)

TP-Detection • Smoother and Faster! • Poor Mean-Square Performances

MDFA

Real-Time Multivariate Filter • `Direct Filter Approach’

Real-Time Filter Cointegration Constraints (Rank=1)

Efficiency (Theorem 4. 1, Wildi 2008, Wildi/Sturm 2008) • The error term e. T is smallest possible uniformly • Uniform efficiency ↔ Customization

Optimal (Efficient) Criterion under Cointegration (Rank=1) • Filter Restrictions are satisfied

Performances MDFA • Output-gap US- and Euro-GDP (2008): – CF and multivariate CF – turning-points anticipated by 1 -2 quarters • USRI – Outperformed Markov-switching (Chauvet, Chauvet/Piger), Dynamic factor models (CFNAI), state space models (ADS), Hodrick. Prescott (OECD-CLI), Christiano-Fitzgerald – SEF-Blog • MDFA-XT • EURI

WARNING!!! • THIS IS NOT A PUSH-THE-BUTTON APPROACH • Formula 1 racer: it can be fast (Ferrari) and reliable (Mercedes) but you have to tweak it carefully: Ferrades/Mercearri – – Filter design (ZPC) Filter constraints (emphasize frequency zero) Understanding/interpreting: `intelligence’ 2008 -Book: http: //www. idp. zhaw. ch/sef • Happy to provide support given financial incentives

Contact/Links

Contact/Links • marc. wildi@zhaw. ch • http: //blog. zhaw. ch/idp/sefblog – Illustrate methodological issues by relying on `realworld‘ projects with economic partners • http: //www. idp. zhaw. ch/usri – Real-Time US Recession Indicator • http: //www. idp. zhaw. ch/MDFA-XT – Experimental Trader for MSCI Emerging Markets – Filters on-line late July • http: //www. idp. zhaw. ch/sef – Signal Extraction & Forecasting Site – Books, Articles, Software