Real Estate in a Mixed-Asset Portfolio The Role

Real Estate in a Mixed-Asset Portfolio: The Role of the Investment Horizon Christian Rehring June 24 2009

Motivation • Goal of the paper § Explore the “term-structure of risk” for direct real estate in addition to classic financial assets § Quantify the influence of the investment horizon on the allocation to real estate in a mixed asset portfolio § By-product: Inflation-hedging abilities of assets depending on the investment-horizon • Factors inducing horizon effects addressed in the paper § Predictable returns § Illiquidity risk § Transaction costs 2

Contributions of my paper • Account for potential mean reversion effect using the cap rate as a state variable § Cap rate/Income return predicts real estate returns (Geltner and Mei, 1995; Fu and Ng, 2001; Plazzi et al. , 2006) § Prior research with direct real estate as an asset class (Geltner et al. (1995), Porras Prado and Verbeek (2008), Mac. Kinnon and Al Zaman (2009)) does not include a state variable, which might capture mean reversion in returns. • Account for real estate market frictions in the form of illiquidity risk (Lin and Vandell, 2007) and transaction costs § Cheng (2008): Optimal holding period for a single property. Analytical solution accounting for transaction costs, predictable returns (positive autocorrelation) and illiquidity risk 3

Modeling approach • Long-term mean variance analysis as in Campbell and Viceira (2005) § Buy-and-hold investor with investment horizon of k years § Investor concerned about real returns § Predictable returns captured by VAR model induce horizon effects in variances/covariances • Augmented by § Transaction costs § Horizon dependent illiquidity risk (marketing period risk factor) 4

VAR(1) model • zt+1 includes § Returns on asset classes – Log real return on cash [r 0, t+1]: basis asset – Log excess returns on real estate, stocks and bonds: § State variables – Log nominal cash return – Log excess return on property share returns – Log cap rate – Log dividend yield – Log yield spread 5

Multiperiod mean and variances • Conditional k-period variance/covariance matrix • Using appropriate selector matrices allows one to calculate variances and covariances of real and nominal returns • Horizons: k = 1 to 20 years • Calculation of variance of real estate returns with and without illiquidity risk premium 6

Asset Allocation problem • Approximation of log portfolio return (Campbell and Viceira, 2002): where • Mean-variance problem 7

Asset Allocation problem • Expected log returns are assumed to take the values of their sample counterparts • Horizon effects in log expected simple returns due to Jensen’s inequality • Round-trip transaction costs for real estate: ln(1+7. 5%); 0% for other assets • Short-selling restriction on real estate 8

Data and sample statistics • UK annual data from 1965 to 2008 • Appraisal-based real estate returns § Data from 1981 to 2008: IPD; 1964 to 1980: Scott (1996). § Unsmoothed with approach proposed by Barkham and Geltner (1994) for annual UK returns: where is the appraisal based real log capital return, gt is the true real log capital return (or growth). a is the smoothing parameter; I use the value 0. 625 as favoured by Barkham and Geltner (1994). • Cap rate: Constructed from capital and total return indices: sum of income in year t divided by price at the end of t. 9

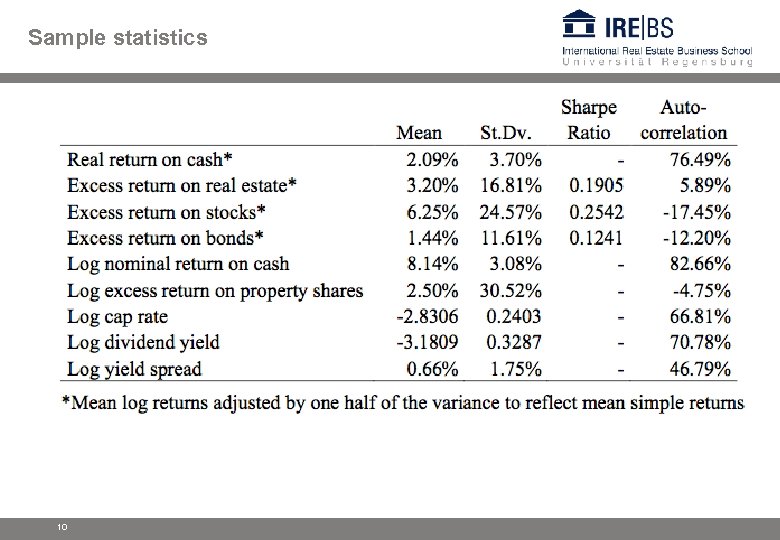Sample statistics 10

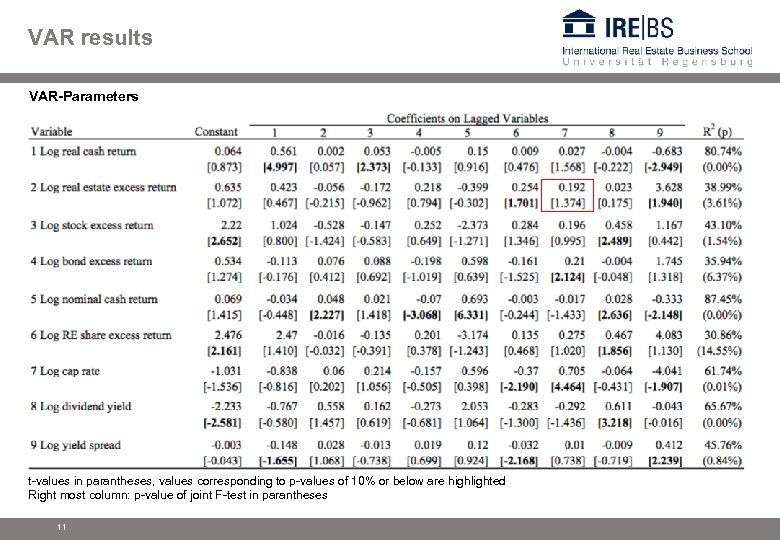VAR results VAR-Parameters t-values in parantheses, values corresponding to p-values of 10% or below are highlighted Right most column: p-value of joint F-test in parantheses 11

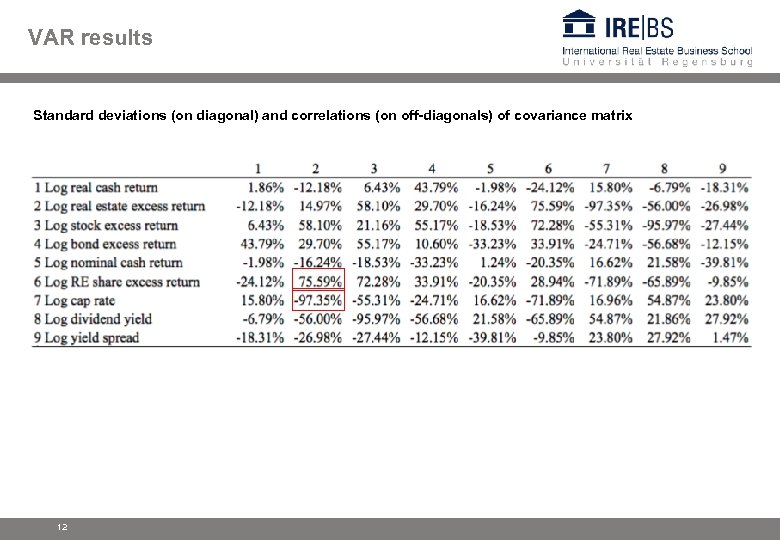VAR results Standard deviations (on diagonal) and correlations (on off-diagonals) of covariance matrix 12

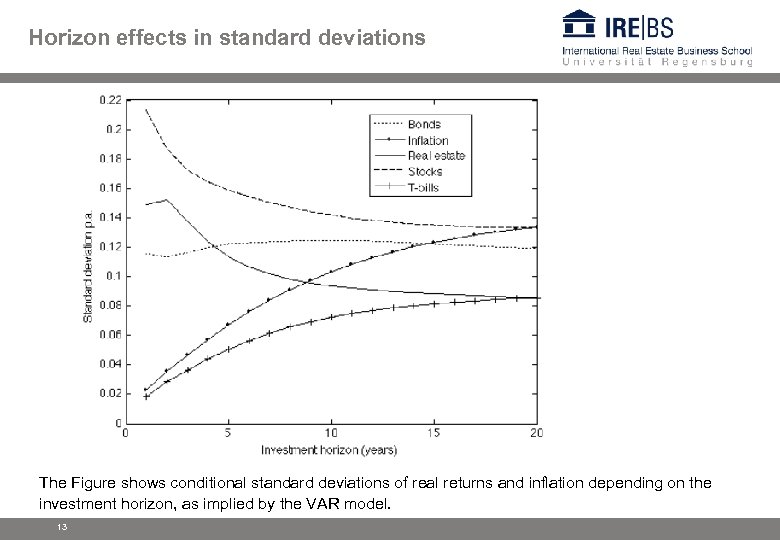Horizon effects in standard deviations The Figure shows conditional standard deviations of real returns and inflation depending on the investment horizon, as implied by the VAR model. 13

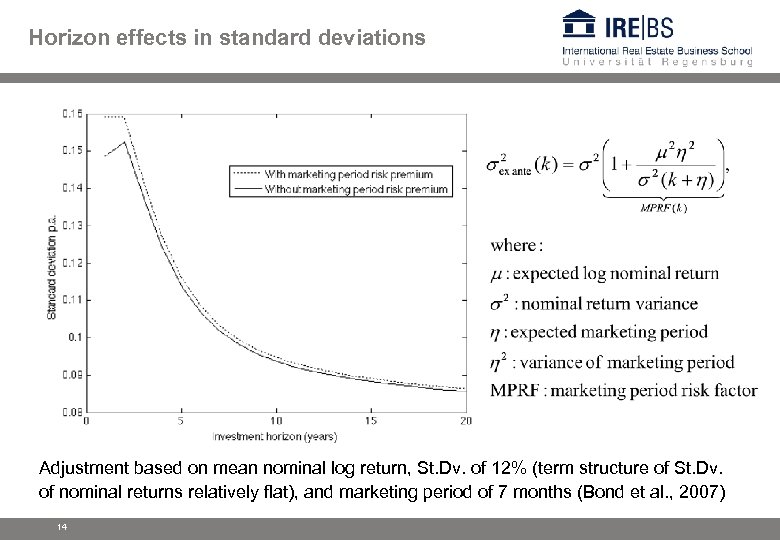Horizon effects in standard deviations Adjustment based on mean nominal log return, St. Dv. of 12% (term structure of St. Dv. of nominal returns relatively flat), and marketing period of 7 months (Bond et al. , 2007) 14

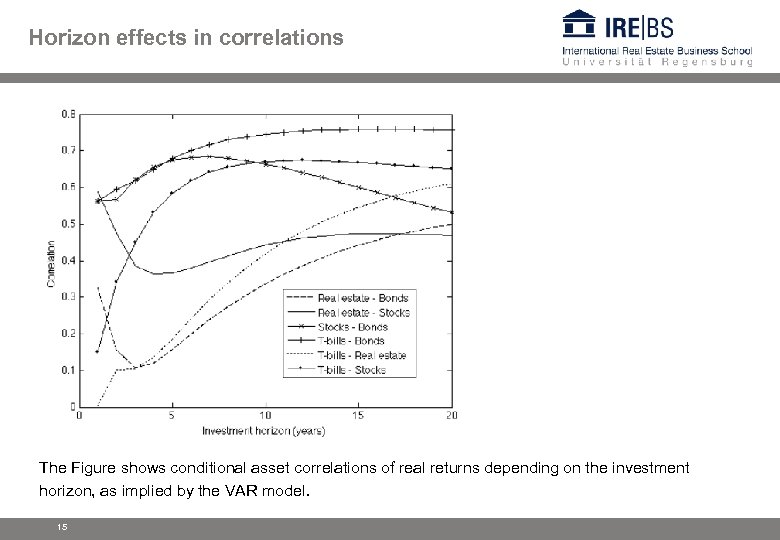Horizon effects in correlations The Figure shows conditional asset correlations of real returns depending on the investment horizon, as implied by the VAR model. 15

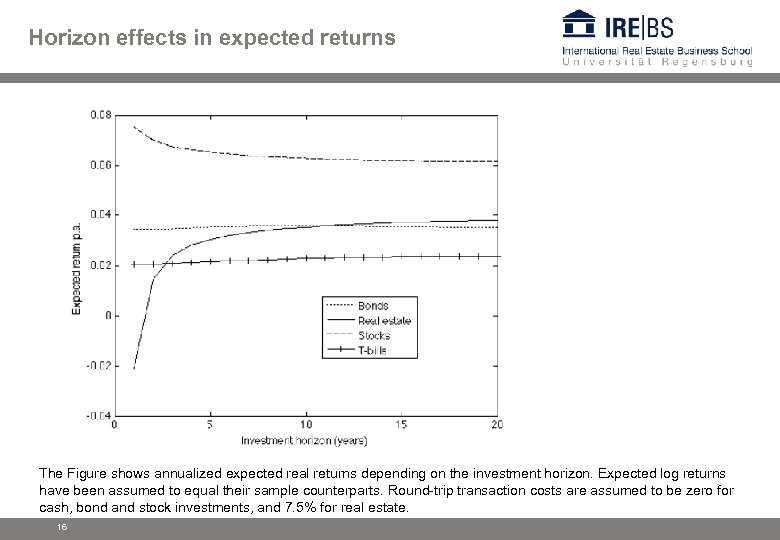Horizon effects in expected returns The Figure shows annualized expected real returns depending on the investment horizon. Expected log returns have been assumed to equal their sample counterparts. Round-trip transaction costs are assumed to be zero for cash, bond and stock investments, and 7. 5% for real estate. 16

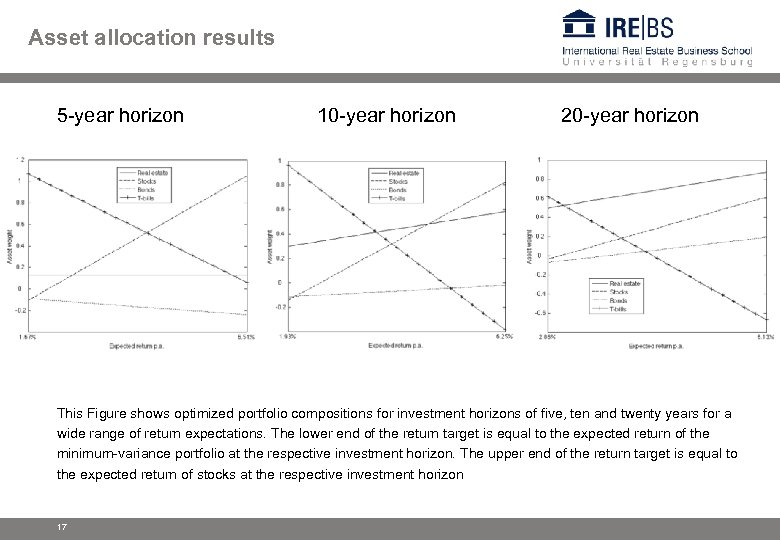Asset allocation results 5 -year horizon 10 -year horizon 20 -year horizon This Figure shows optimized portfolio compositions for investment horizons of five, ten and twenty years for a wide range of return expectations. The lower end of the return target is equal to the expected return of the minimum-variance portfolio at the respective investment horizon. The upper end of the return target is equal to the expected return of stocks at the respective investment horizon 17

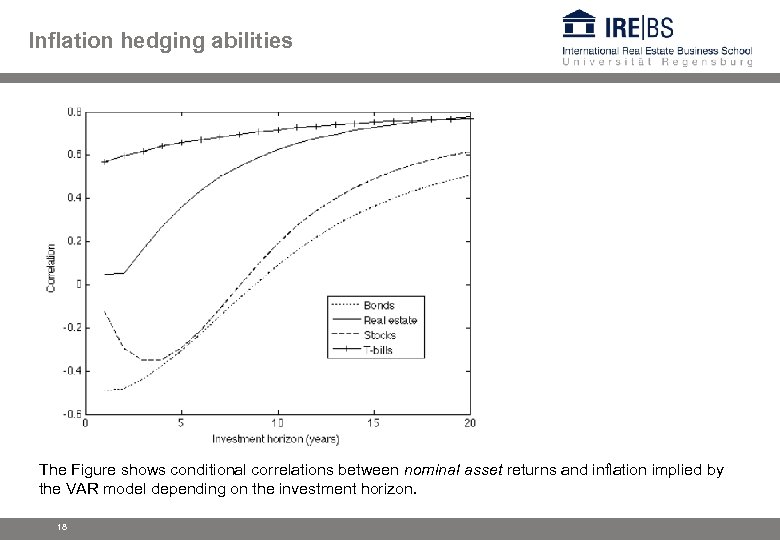Inflation hedging abilities The Figure shows conditional correlations between nominal asset returns and inflation implied by the VAR model depending on the investment horizon. 18

Conclusion • UK real estate returns show slight mean aversion over short investment horizons and strong mean reversion over medium and long horizons. • An illiquidity risk premium accentuates the mean reversion effect. • The return correlations of real estate with the other assets are relatively favourable, even in the long run. • The weight assigned to real estate is increasing with the investment horizon. Over medium and long investment horizons, and over a wide range of return targets, the weight allocated to real estate is between 13% and 87%. • Real estate appears to be a very good inflation hedge in the long run, but not on a short-term basis. 19

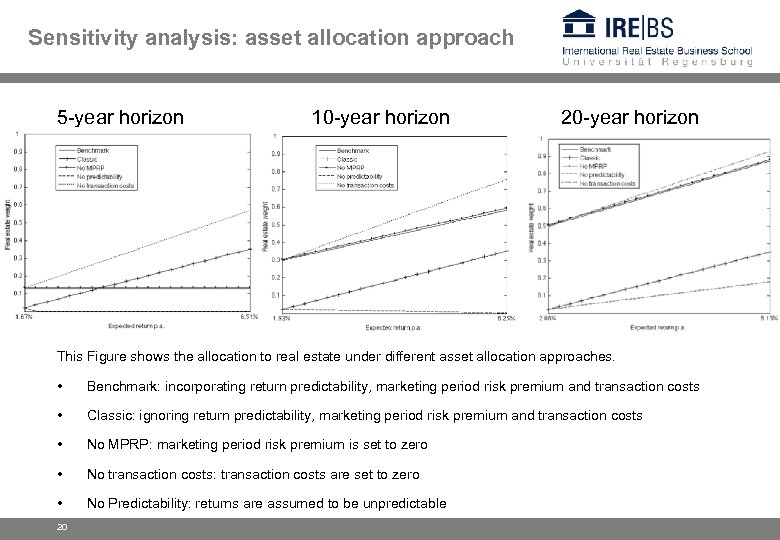Sensitivity analysis: asset allocation approach 5 -year horizon 10 -year horizon 20 -year horizon This Figure shows the allocation to real estate under different asset allocation approaches. • Benchmark: incorporating return predictability, marketing period risk premium and transaction costs • Classic: ignoring return predictability, marketing period risk premium and transaction costs • No MPRP: marketing period risk premium is set to zero • No transaction costs: transaction costs are set to zero • No Predictability: returns are assumed to be unpredictable 20

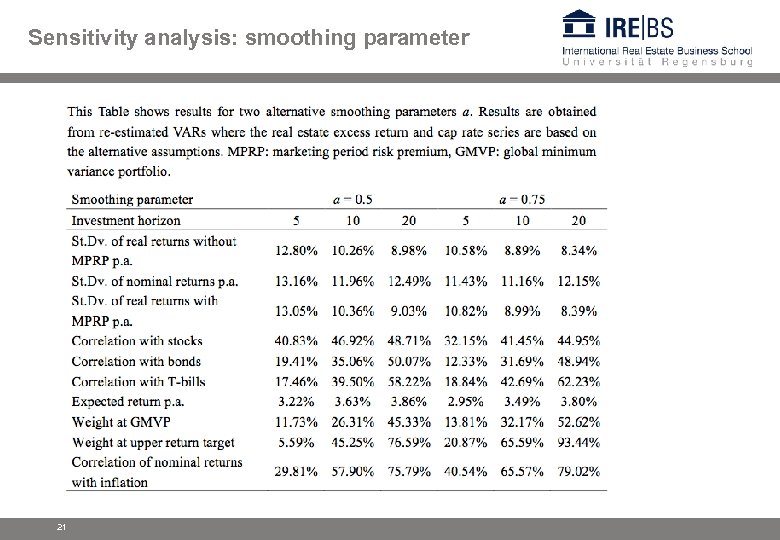Sensitivity analysis: smoothing parameter 21