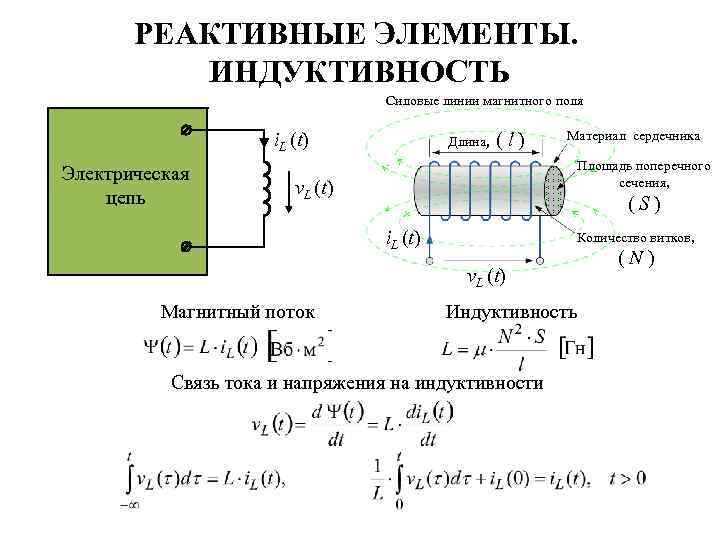
РЕАКТИВНЫЕ ЭЛЕМЕНТЫ ИНДУКТИВНОСТЬ Силовые линии магнитного поля Длина

РЕАКТИВНЫЕ ЭЛЕМЕНТЫ. ИНДУКТИВНОСТЬ Силовые линии магнитного поля Длина, i. L (t) Электрическая цепь (l) Материал сердечника Площадь поперечного сечения, v. L (t) (S) i. L (t) Количество витков, v. L (t) Магнитный поток Индуктивность Связь тока и напряжения на индуктивности (N)

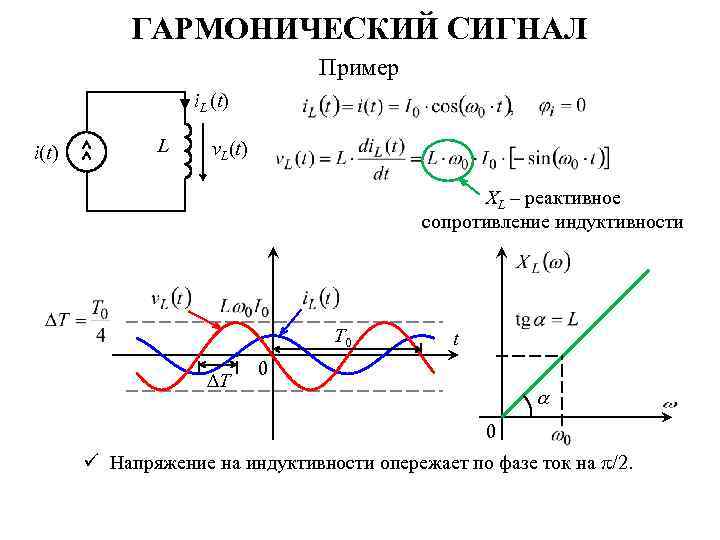ГАРМОНИЧЕСКИЙ СИГНАЛ Пример i. L (t) i(t) L v. L(t) XL – реактивное сопротивление индуктивности T 0 T t 0 0 ü Напряжение на индуктивности опережает по фазе ток на /2.

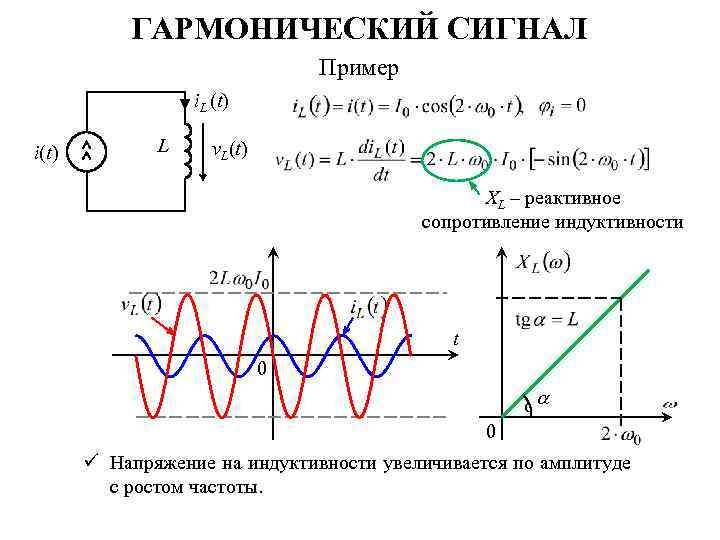ГАРМОНИЧЕСКИЙ СИГНАЛ Пример i. L (t) i(t) L v. L(t) XL – реактивное сопротивление индуктивности t 0 с 0 ü Напряжение на индуктивности увеличивается по амплитуде с ростом частоты.

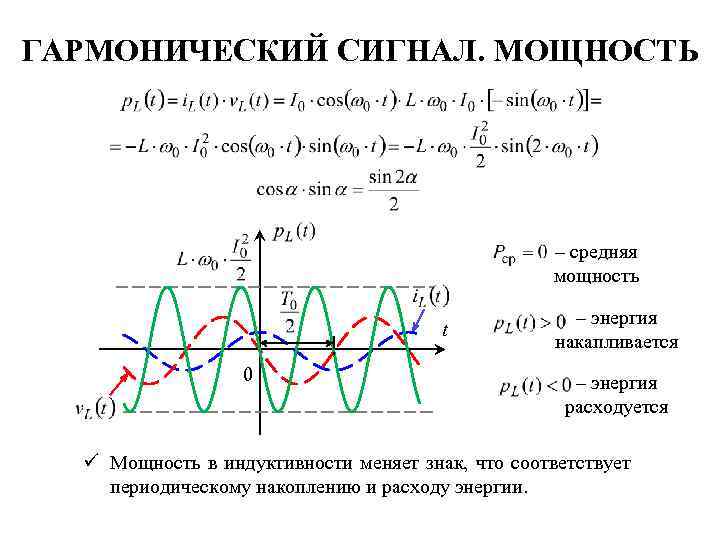ГАРМОНИЧЕСКИЙ СИГНАЛ. МОЩНОСТЬ – средняя мощность t 0 – энергия накапливается – энергия расходуется ü Мощность в индуктивности меняет знак, что соответствует периодическому накоплению и расходу энергии.

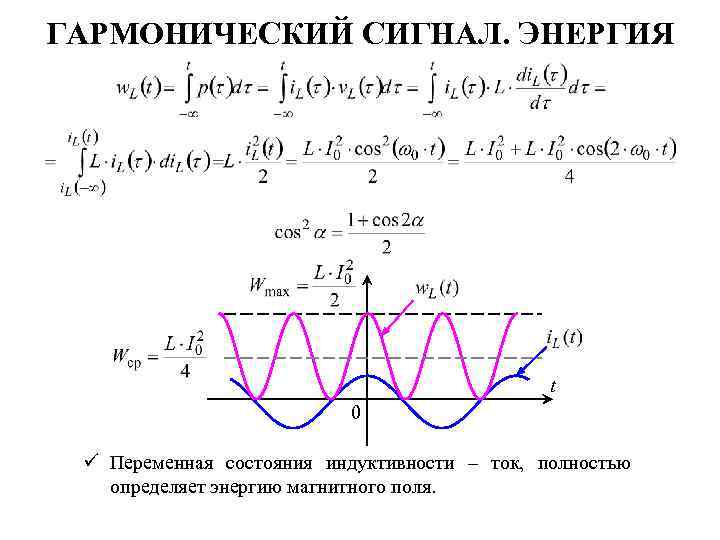ГАРМОНИЧЕСКИЙ СИГНАЛ. ЭНЕРГИЯ t 0 ü Переменная состояния индуктивности – ток, полностью определяет энергию магнитного поля.

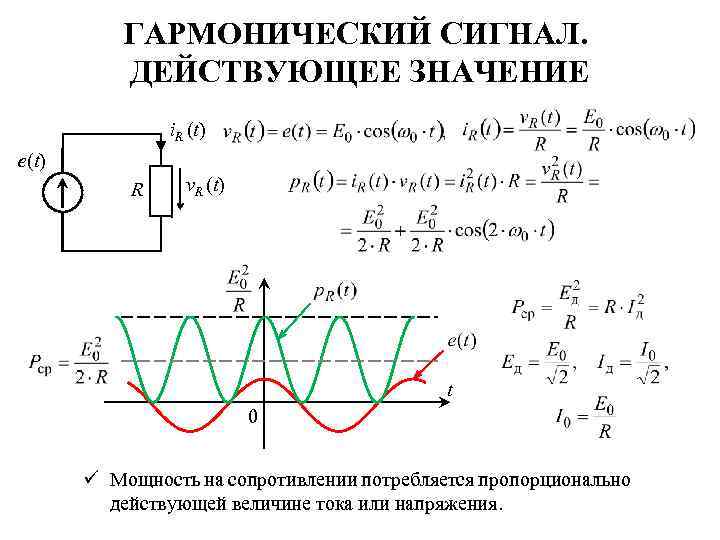ГАРМОНИЧЕСКИЙ СИГНАЛ. ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ i. R (t) e(t) R v. R (t) t 0 ü Мощность на сопротивлении потребляется пропорционально действующей величине тока или напряжения.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ R Пример i(t) Дано: e(t) v. R(t) С v. С(t) Найти: – динамическое уравнение – дифференциальное уравнение (канонический вид)

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ Подстановка: и – неизвестны

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ XС – реактивное сопротивление емкости

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ Пример R Дано: С Найти: комплексная экспонента – динамическое уравнение – дифференциальное уравнение (канонический вид)

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ Подстановка: и – неизвестны

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ Подстановка: и – неизвестны

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ Подстановка: и – неизвестны

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ Подстановка: и – неизвестны

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ Подстановка: и – неизвестны

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ Подстановка: и – неизвестны

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ

КОМПЛЕКСНЫЕ АМПЛИТУДЫ R Дано: Найти: Решение:

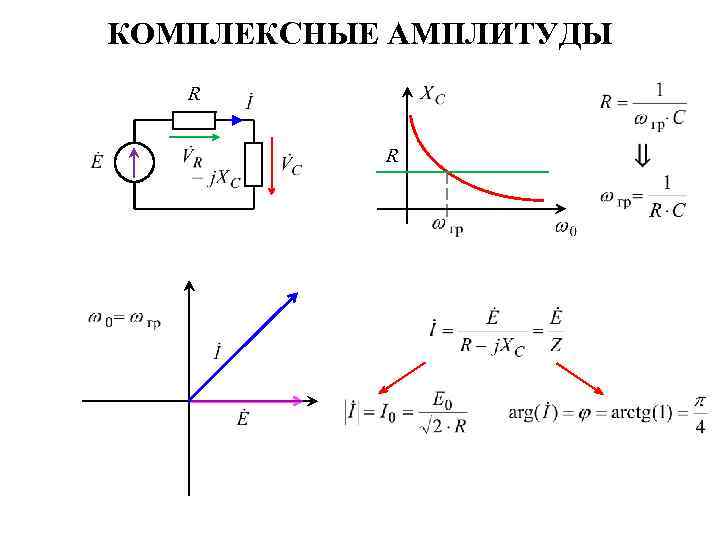КОМПЛЕКСНЫЕ АМПЛИТУДЫ R R

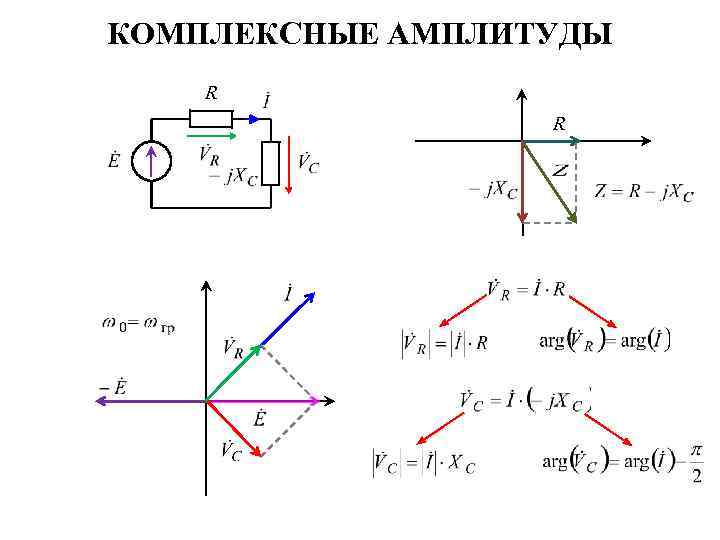КОМПЛЕКСНЫЕ АМПЛИТУДЫ R R

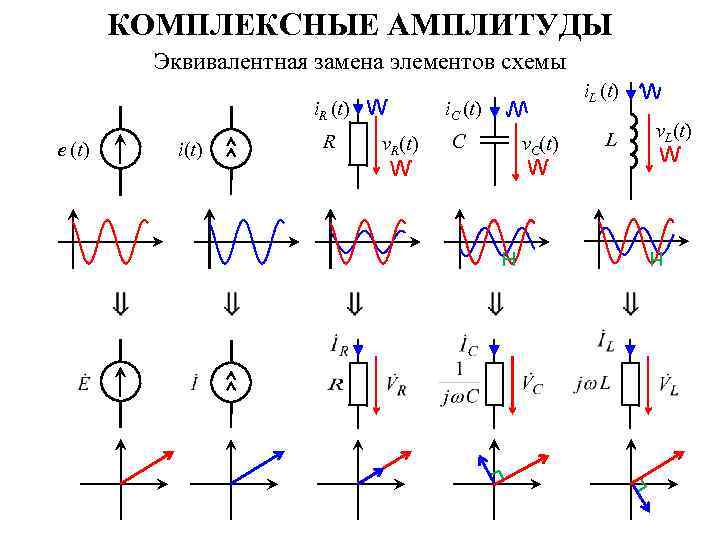КОМПЛЕКСНЫЕ АМПЛИТУДЫ Эквивалентная замена элементов схемы i. R (t) e (t) R i(t) i. L (t) i. C (t) v. R(t) C v. C(t) L v. L(t)

КОМПЛЕКСНЫЕ ЧИСЛА y 0 y x

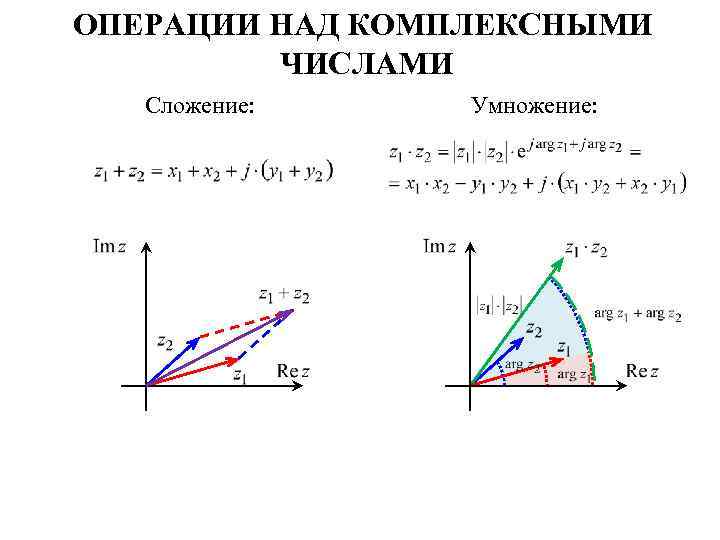ОПЕРАЦИИ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ Сложение: Умножение:

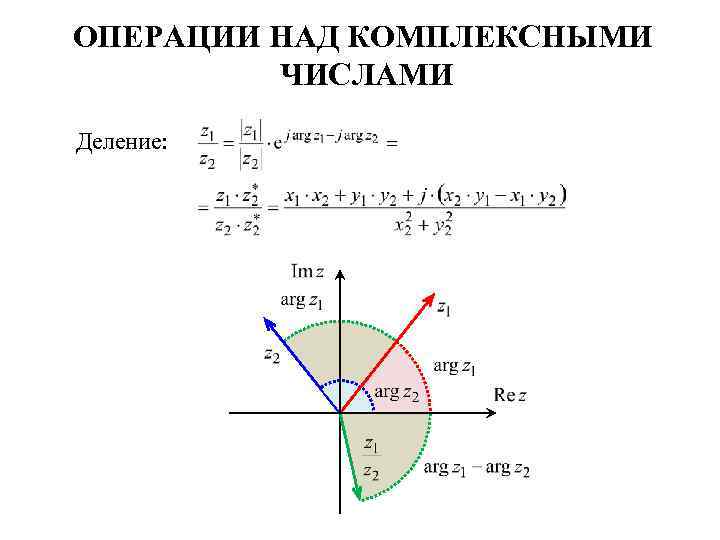ОПЕРАЦИИ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ Деление: