Reaching Agreements Voting 7 -1 Voting Truthful

Strategic (insincere) voters n n n Suppose your choice will likely come in second place. If you rank the first choice of rest of group very low, you may lower that choice enough so yours is first. True story. Dean’s selection. Each committee member told they had 5 points to award and could spread out any way among the candidates. The recipient of the most points wins. I put all my points on one candidate. Most split their points. I swung the vote! What was my gamble? Want to get the results as if truthful voting were done. 9

Typical Competition Mechanisms n n n Auction: allocate goods or tasks to agents through market. Need a richer technique for reaching agreements Negotiation: reach agreements through interaction. Argumentation: resolve confliction through debates. 10

Reaching Agreements: Voting 7 -11

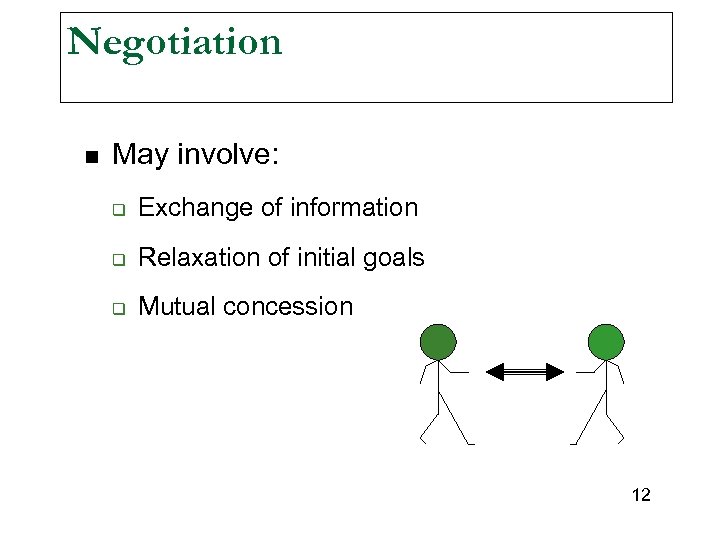Negotiation n May involve: q Exchange of information q Relaxation of initial goals q Mutual concession 12

Mechanisms, Protocols, Strategies n Negotiation is governed by a mechanism or a protocol: q defines the ”rules of encounter” between the agents q the public rules by which the agents will come to agreements. q q n The deals that can be made The sequence of offers and counter-offers that can be made Given a particular protocol, how can a particular strategy be designed that individual agents can use? 13

Negotiation Mechanism Negotiation is the process of reaching agreements on matters of common interest. It usually proceeds in a series of rounds, with every agent making a proposal at every round. Issues in negotiation process: • Negotiation Space: All possible deals that agents can make, i. e. , the set of candidate deals. • Negotiation Protocol: – A rule that determines the process of a negotiation: how and when a proposal can be made, when a deal has been struck, when the negotiation should be terminated, and so. • Negotiation Strategy: When and what proposals should be made. 7 -14

Protocol n n Means kinds of deals that can be made Means sequence of offers and counter-offers Protocol is like rules of chess game, whereas strategy is way in which player decides which move to make Do we even understand what is up for grabs? We may ask for a raise without considering bigger office, different appointment, 4 -day work week, etc. 15

Negotiation Protocol n n n n Who begins Take turns Build off previous offers Give feed back (or not). Tell what utility is (or not) Obligations – requirements for later Privacy Allowed proposals you can make as a result of negotiation history 16

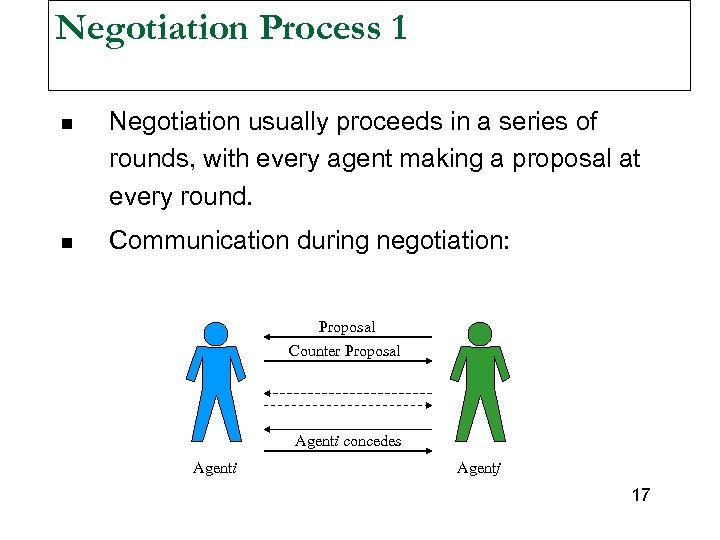Negotiation Process 1 n Negotiation usually proceeds in a series of rounds, with every agent making a proposal at every round. n Communication during negotiation: Proposal Counter Proposal Agenti concedes Agenti Agentj 17

Negotiation Process 2 n Another way of looking at the negotiation process is (can talk about 50/50 or 90/10 depending on who ”moves” the farthest): Proposals by Ai Point of Acceptance/ aggreement Proposals by Aj 18

Jointly Improving Direction method Iterate over n Mediator helps players criticize a tentative agreement (could be status quo) n Generates a compromise direction (where each of the k issues is a direction in k-space) n Mediator helps players to find a jointly preferred outcome along the compromise direction, and then proposes a new tentative agreement. 19

Example: list of things to be done. Assigned to individuals already n Who does what n n What is order to do What is paid for tasks 20

Goals of Negotiation (in many cases) n n n Efficiency – not waste utility. Pareto Opt Stability – no agent have incentive to deviate from agreed-upon strategy (as in one-shot negotiation). Simplicity – low computational demands on agents Distribution – interaction rules not require a central decision maker Symmetry – (in some cases) may not want agents to play different roles. 21

Example: n n Planes need to be assigned landing time. Rule could be that airplanes with less fuel land first. Any disadvantage? 22

Slotted Blocks world n n Like blocks world, only a fixed number of slots on table. Forces need to coordinate Ex: Need to share car. Has side effects Ex: Schedule classes/professors – no side effect. 23

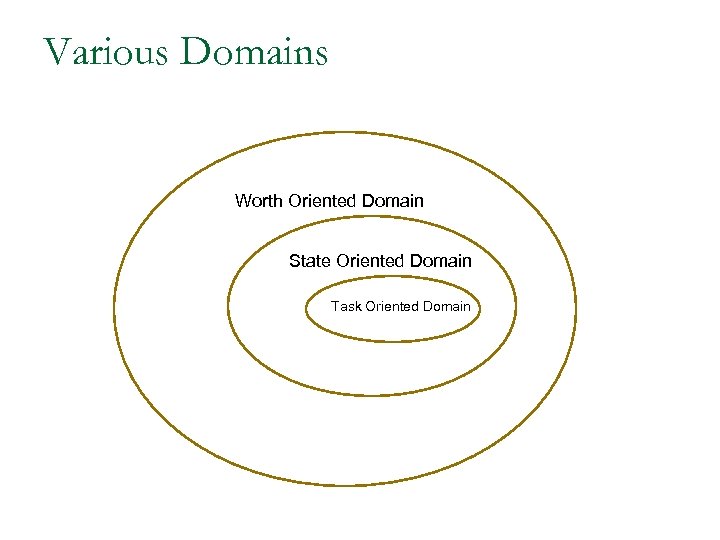Various Domains Worth Oriented Domain State Oriented Domain Task Oriented Domain

Typical Negotiation Problems Task-Oriented Domains(TOD): an agent's activity can be defined in terms of a set of tasks that it has to achieve. The target of a negotiation is to minimize the cost of completing the tasks. State Oriented Domains(SOD): each agent is concerned with moving the world from an initial state into one of a set of goal states. The target of a negotiation is to achieve a common goal. Main attribute: actions have side effects (positive/negative). TOD is a subset of SOD. Most classical AI domains are instances of SOD. Main attribute of SOD – actions have side effects. Agents can unintentionally achieve one another’s goals. Negative interactions can also occur. Worth Oriented Domains(WOD): agents assign a worth to each potential state, which captures its desirability for the agent. The target of a negotiation is to maximize mutual worth (rather than worth to individual). Superset of SOD. Rates the acceptability of final states. Allows agents to compromise 25 on their goals.

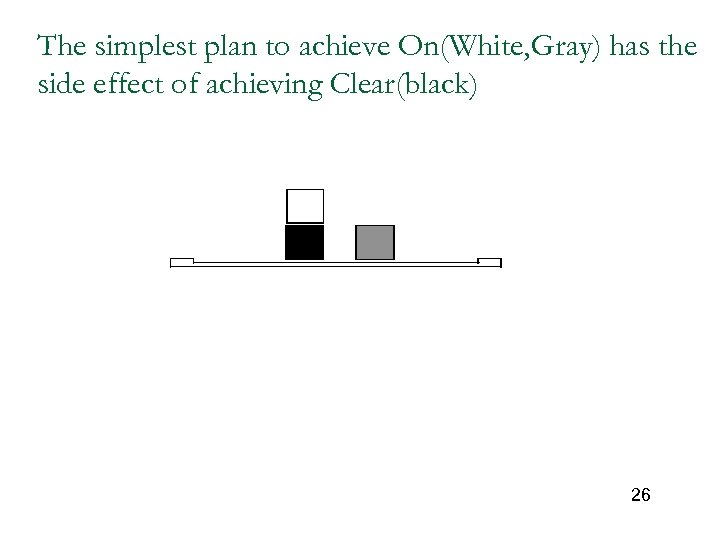The simplest plan to achieve On(White, Gray) has the side effect of achieving Clear(black) 26

Single issue negotiation n n Like money Symmetric (If roles were reversed, I would benefit the same way you would) q q n If one task requires less travel, both would benefit equally by having less travel utility for a task is experienced the same way by whomever is assigned to that task. Non-symmetric – we would benefit differently if roles were reversed q if you delivered the picnic table, you could just throw it in the back of your van. If I delivered it, I would have to rent a Uhaul to transport it (as my car is small). 27

Multiple Issue negotiation n n Could be hundreds of issues (cost, delivery date, size, quality) Some may be inter-related (as size goes down, cost goes down, quality goes up? ) Not clear what a true concession is (larger may be cheaper, but harder to store or spoils before can be used) May not even be clear what is up for negotiation (I didn’t realize not having any test was an option) (on the job…Ask for stock options, bigger office, work from home. ) 28

How many agents are involved? n n n One to one One to many (auction is an example of one seller and many buyers) Many to many (could be divided into buyers and sellers, or all could be identical in role) q n(n-1)/2 number of pairs 29

Negotiation Domains: Task-oriented n ”Domains in which an agent’s activity can be defined in terms of a set of tasks that it has to achieve”, (Rosenschein & Zlotkin, 1994) n An agent can carry out the tasks without interference (or help) from other agents – such as ”who will deliver the mail” n All resources are available to the agent n Tasks redistributed for the benefit of all agents 30

Task-oriented Domain: Definition n How can an agent evaluate the utility of a specific deal? q Utility represents how much an agent has to gain from the deal. (it is always based on change from original allocation) q Since an agent can achieve the goal on its own, it can compare the cost of achieving the goal on its own to the cost of its part of the deal. n n If utility<0, it is worse off than performing tasks on its own. Conflict deal: (stay with status quo) if agents fail to reach an agreement: q where no agent agrees to execute tasks other than its own. n utlity = 0 31

Formalization of TOD A Task Oriented Domain(TOD) is a triple where: q T is a finite set of all possible tasks; q Ag={A 1, A 2, …, An} is a list of participant agents; q c: (T) R+ defines cost of executing each subset of tasks. Assumptions on cost function: 1. c( ) = 0. 2. The cost of a subset of tasks does not depend on who carries out them. (Idealized situation) 3. Cost function is monotonic, which means that more tasks, more cost. (It can’t cost less to take on more tasks. ) 32 i. T 1 T 2 implies c(T 1) c(T 2)

Redistribution of Tasks Given a TOD , T is original assignment, output is D: assignment after the “deal” n An encounter (instance) within the TOD is an ordered list (T 1, T 2) such that for all k, Tk T. This is an original allocation of tasks that they might want to reallocate. n A pure deal on an encounter is the redistribution of tasks among agents: (D 1, D 2), such that all tasks are reassigned D 1 D 2= T 1 T 2 Specifically, : (D 1, D 2)=(T 1, T 2) is called the conflict deal. n For each deal =(D 1, D 2), the cost of such a deal to agent k is Costk( )=c(Dk) (i. e, cost to k of deal is cost of Dk, k’s part of deal) 33

Examples of TOD Parcel Delivery: Several couriers have to deliver sets of parcels to different cities. The target of negotiation is to reallocate deliveries so that the cost of travel to each courier is minimal. n Database Queries: Several agents have access to a common database, and each has to carry out a set of queries. The target of negotiation is to arrange queries so as to maximize efficiency of database operations (Join, Projection, Union, Intersection, …). You are doing a join as part of another operation, so please save the results for me. n 34

Possible Deals Consider an encounter from the Parcel Delivery Domain. Suppose we have two agents. Both agents have parcels to deliver to city a and only agent 2 has parcels to deliver to city b. There are nine distinct pure deals in this encounter: 6. ({b}, {a, b}) 1. ({a}, {b}) 7. ({a, b}, {a}) 2. ({b}, {a}) 8. ({a, b}, {b}) 3. ({a, b}, ) 9. ({a, b}, {a, b}) 4. ( , {a, b}) 5. ({a}, {a, b}) the conflict deal 35

Figure deals knowing union must be {ab} n n n Choices for first agent: {a} {b} {ab} {} Second agent must “pick up the slack” {a} for agent 1 b|ab (for agent 2) {b} for agent 1 a|ab {ab} for agent 1 a|ab|b|{} {} for agent 1 ab 36

Utility Function for Agents Given an encounter (T 1, T 2), the utility function for each agent is just the difference of costs and is defined as follow: Utilityk( )=c(Tk)-Costk( ) = c(Tk)- c(Dk) where q q q =(D 1, D 2) is a deal; c(Tk) is the stand-alone cost to agent k (the cost of achieving its original goal with no help) Costk( ) is the cost of its part of the deal. Note that the utility of the conflict deal is always 0. 37

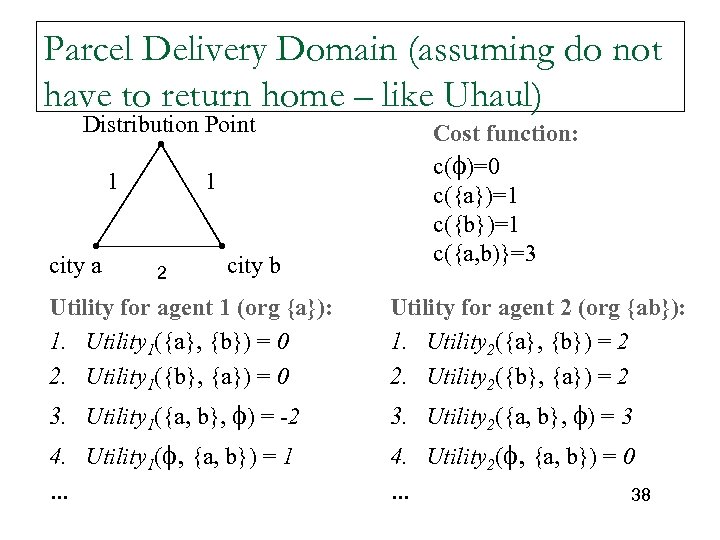Parcel Delivery Domain (assuming do not have to return home – like Uhaul) Distribution Point 1 city a 1 2 city b Cost function: c( )=0 c({a})=1 c({b})=1 c({a, b)}=3 Utility for agent 1 (org {a}): 1. Utility 1({a}, {b}) = 0 2. Utility 1({b}, {a}) = 0 Utility for agent 2 (org {ab}): 1. Utility 2({a}, {b}) = 2 2. Utility 2({b}, {a}) = 2 3. Utility 1({a, b}, ) = -2 3. Utility 2({a, b}, ) = 3 4. Utility 1( , {a, b}) = 1 … 4. Utility 2( , {a, b}) = 0 … 38

Dominant Deals n Deal dominates deal ' if is better for at least one agent and not worse for the other, i. e. , q is at least as good for every agent as ': k {1, 2}, Utilityk( ) Utilityk( ') q is better for some agent than ': k {1, 2}, Utilityk( )> Utilityk( ') n Deal weakly dominates deal ' if at least the first condition holds (deal isn’t worse for anyone). Any reasonable agent would prefer (or go along with) over ' if dominates or weakly dominates '. 39

Negotiation Set: Space of Negotiation n A deal is called individual rational if weakly dominates the conflict deal. (no worse than what you have already) A deal is called Pareto optimal if there does not exist another deal ' that dominates . (best deal for x without disadvantaging y) The set of all deals that are individual rational and Pareto optimal is called the negotiation set (NS). 40

Utility Function for Agents (example from previous slide) 1. 2. 3. 4. 5. 6. 7. 8. 9. Utility 1({a}, {b}) =0 Utility 1({b}, {a})=0 Utility 1({a, b}, )=-2 Utility 1( , {a, b})=1 Utility 1({a}, {a, b})=0 Utility 1({b}, {a, b})=0 Utility 1({a, b}, {a})=-2 Utility 1({a, b}, {b})=-2 Utility 1({a, b}, {a, b})= -2 1. Utility 2({a}, {b}) =2 2. Utility 2 ({b}, {a})=2 3. Utility 2 ({a, b}, )=3 4. Utility 2 ( , {a, b})=0 5. Utility 2 ({a}, {a, b})=0 6. Utility 2 ({b}, {a, b})=0 7. Utility 2 ({a, b}, {a})=2 8. Utility 2 ({a, b}, {b})=2 9. Utility 2 ({a, b}, 41 {a, b})=0

Individual Rational for Both (eliminate any choices that are negative for either) 1. 2. 3. 4. 5. 6. 7. 8. 9. ({a}, {b}) ({b}, {a}) ({a, b}, ) ( , {a, b}) ({a}, {a, b}) ({b}, {a, b}) ({a, b}, {a}) ({a, b}, {b}) ({a, b}, {a, b}) individual rational ({a}, {b}) ({b}, {a}) ( , {a, b}) ({a}, {a, b}) ({b}, {a, b}) 42

Pareto Optimal Deals 1. 2. 3. 4. 5. 6. 7. 8. 9. ({a}, {b}) ({b}, {a}) ({a, b}, ) ( , {a, b}) ({a}, {a, b}) ({b}, {a, b}) ({a, b}, {a}) ({a, b}, {b}) ({a, b}, {a, b}) is (-2, 3), but nothing beats 3 for agent 2 Pareto Optimal Beaten by ({a}{b}) deal ({a}, {b}) ({b}, {a}) ({a, b}, ) ( , {a, b}) 43

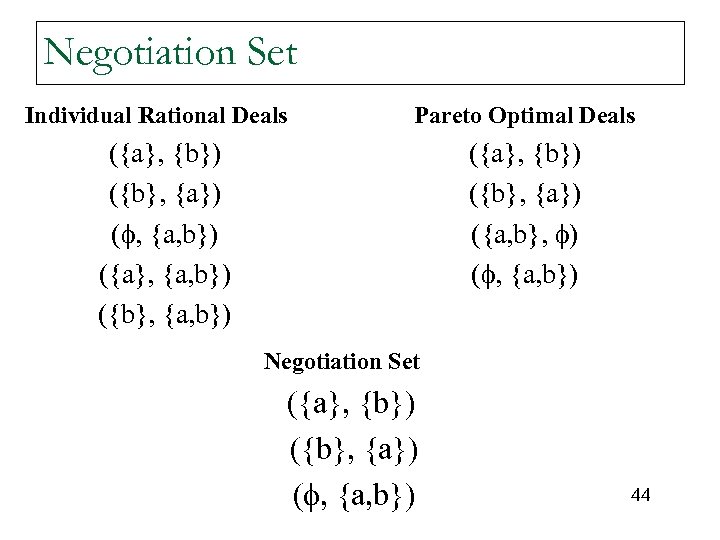Negotiation Set Individual Rational Deals Pareto Optimal Deals ({a}, {b}) ({b}, {a}) ( , {a, b}) ({a}, {a, b}) ({b}, {a, b}) ({a}, {b}) ({b}, {a}) ({a, b}, ) ( , {a, b}) Negotiation Set ({a}, {b}) ({b}, {a}) ( , {a, b}) 44

Negotiation Set illustrated n n n Create a scatter plot of the utility for i over the utility for j Only those where both is positive are individually rational (for both) (origin is conflict deal) Which are pareto optimal? Utility for i Utility for j 45

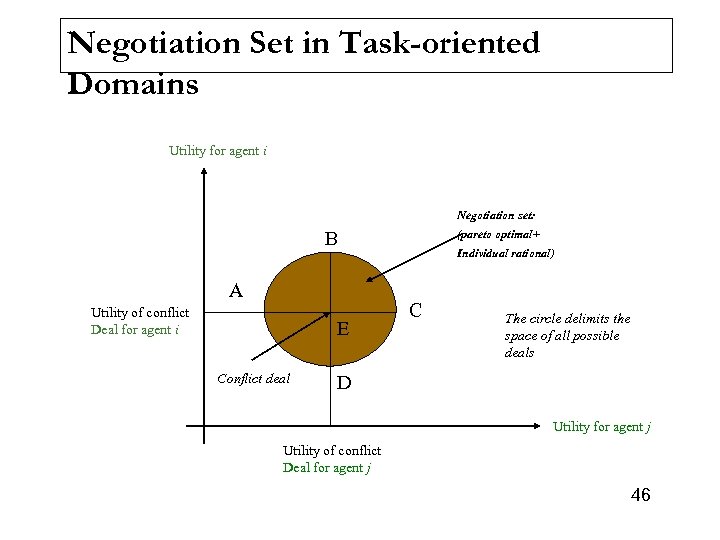Negotiation Set in Task-oriented Domains Utility for agent i Negotiation set: B A Utility of conflict Deal for agent i E Conflict deal (pareto optimal+ Individual rational) C The circle delimits the space of all possible deals D Utility for agent j Utility of conflict Deal for agent j 46

Negotiation Protocol n n P( ) – Product of the two agent utilities from product maximizing negotiation protocol One step protocol q n At time t >= 0, A offers (A, t) and B offers (B, t), such that q q q n Concession protocol Both deals are from the negotiation set i e {A, B} and t >0, Utilityi( (i, t)) <= Utilityi( (i, t-1)) I propose something less desirable for me Negotiation ending q q Conflict - Utilityi( (i, t)) = Utilityi( (i, t-1)) Agreement, j !=i e {A, B}, Utilityj( (i, t)) >= Utilityj( (j, t)) n n Pure Only A => agree (B, t) either agrees with proposal of other deals Only B => agree (A, t) either agrees with proposal of other Both A, B => agree (k, t) such that P( (k))=max{P( (A)), P( (B))} Both A, B and P( (A))=P( (B)) => flip a coin (product is the same, but may not be the same for each agent – flip coin to decide which deal to use) 47 Mixed deal

The Monotonic Concession Protocol – One direction, move towards middle Rules of this protocol are as follows. . . n Negotiation proceeds in rounds. n On round 1, agents simultaneously propose a deal from the negotiation set [individually rational, pareto optimal). Can re-propose same deal. n Agreement is reached if one agent finds that the deal proposed by the other is at least as good or better than its proposal. n If no agreement is reached, then negotiation proceeds to another round of simultaneous proposals. n An agent is not allowed to offer the other agent less (in term of utility ) than it did in the previous round. It can either stand still or make a concession. Assumes we know what the other agent values. n If neither agent makes a concession in some round, then negotiation terminates, with the conflict deal. n Meta data may be present: explanation or critique of deal. 48

Condition to Consent an Agreement If both of the agents finds that the deal proposed by the other is at least as good or better than the proposal it made. Utility 1( 2) Utility 1( 1) and Utility 2( 1) Utility 2( 2) 49

The Monotonic Concession Protocol Advantages: n q Symmetrically distributed (no agent plays a special role) q Ensures convergence q It will not go on indefinitely Disadvantages: n q Agents can run into conflicts q Inefficient – no quarantee that an agreement will be reached quickly 50

Negotiation Strategy Given the negotiation space and the Monotonic Concession Protocol, a strategy of negotiation is an answer to the following questions: n What should an agent’s first proposal be? n On any given round, who should concede? n If an agent concedes, then how much should it concede? 51

The Zeuthen Strategy – a refinement of monotonic protocol Q: What should my first proposal be? A: the best deal for you among all possible deals in the negotiation set. (Is a way of telling others what you value. ) Agent 1's best deal agent 2's best deal 52

Example of Zeuthan n n In interviewing for Women’s center director, the candidate we were most interested in was approached. She started by asking for q q $10 K more money Job for husband Tenured full professor in academic department Gold parking pass for terrace 53

What was her strategy? n n n Clearly Zeuthan Advantages: she had something to concede and we knew what she valued Disadvantage: could be thought of as too much so that the committee removes her from the pool. Have had students make “initial request” that backfired as seemed totally off-base. If you realize someone is using this strategy, you might NOT be offended. 54

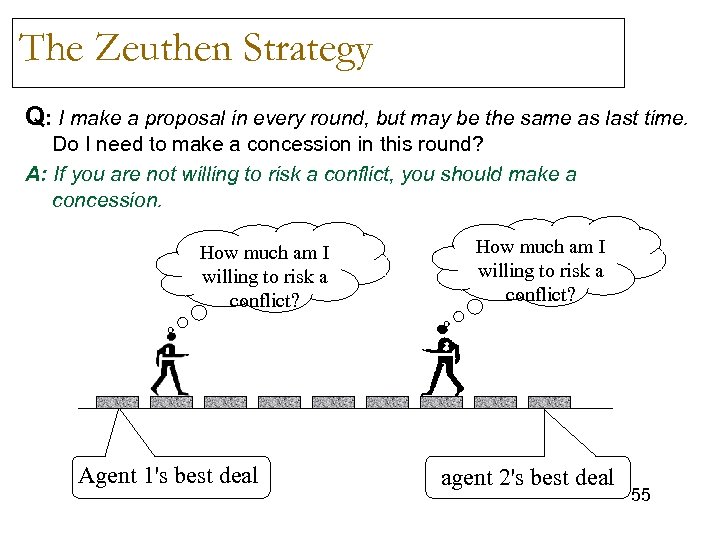The Zeuthen Strategy Q: I make a proposal in every round, but may be the same as last time. Do I need to make a concession in this round? A: If you are not willing to risk a conflict, you should make a concession. How much am I willing to risk a conflict? Agent 1's best deal How much am I willing to risk a conflict? agent 2's best deal 55

Willingness to Risk Conflict Suppose you have conceded a lot. Then: – You have lost some of your expected utility (closer to zero). – In case conflict occurs, you are not much worse off. – An agent will be more willing to risk conflict if the difference in utility between the loss in making an concession is greater than the loss in taking a conflict deal with respect to the current offer. n If both are equally willing to risk, both concede. 56

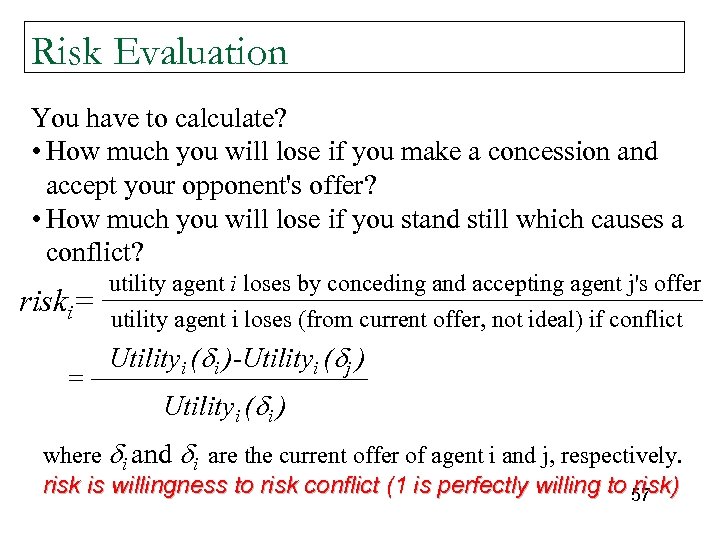Risk Evaluation You have to calculate? • How much you will lose if you make a concession and accept your opponent's offer? • How much you will lose if you stand still which causes a conflict? riski= = utility agent i loses by conceding and accepting agent j's offer utility agent i loses (from current offer, not ideal) if conflict Utilityi ( i )-Utilityi ( j ) Utilityi ( i ) where i and i are the current offer of agent i and j, respectively. risk is willingness to risk conflict (1 is perfectly willing to 57 risk)

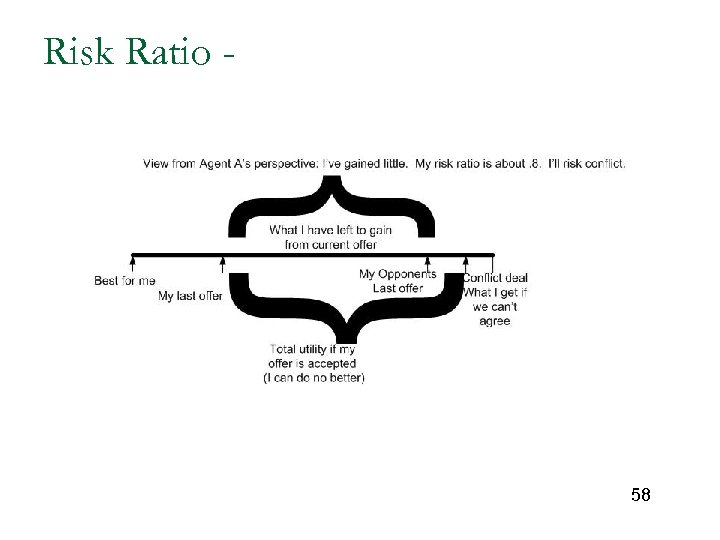Risk Ratio - 58

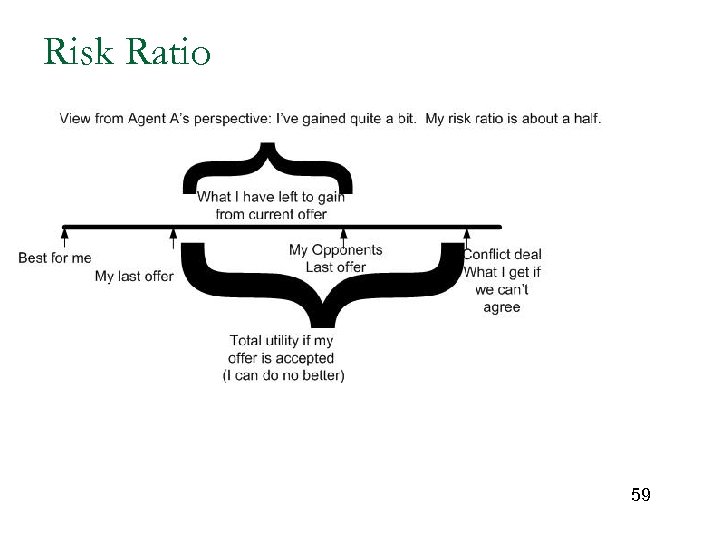Risk Ratio 59

Risk Evaluation n n risk measures the fraction you have left to gain. If it is close to one, you have gained little (and are more willing to risk). This assumes you know what others utility is. Which is not always the case. If we have such perfect knowledge, we can compute the deal immediately. More likely, we base our decisions on what we THINK the other’s utility is. You may not agree with their “concept” of utility – as they “claim” certain concessions or expectations. In the car example, your initial price would be important. What one sets as initial goal affects risk. If I set an impossible goal, my willingness to risk is always higher. 60

The Zeuthen Strategy Q: If I concedes, then how much should I concede? A: Enough to change the balance of risk (who has more to lose). (Otherwise, it will just be your turn to concede again at the next round) Not so much that you give up more than you needed to Q: What if both have equal risk? A: Both concede. 61

About MCP and Zeuthen Strategies Advantages: n q Simple and reflects the way human negotiations work. q Stability – in Nash equilibrium – if one agent is using the strategy, then the other can do no better than using it him/herself. Disadvantages: n q Computationally expensive – players need to compute the entire negotiation set. q Communication burden – negotiation process may involve several steps. 62

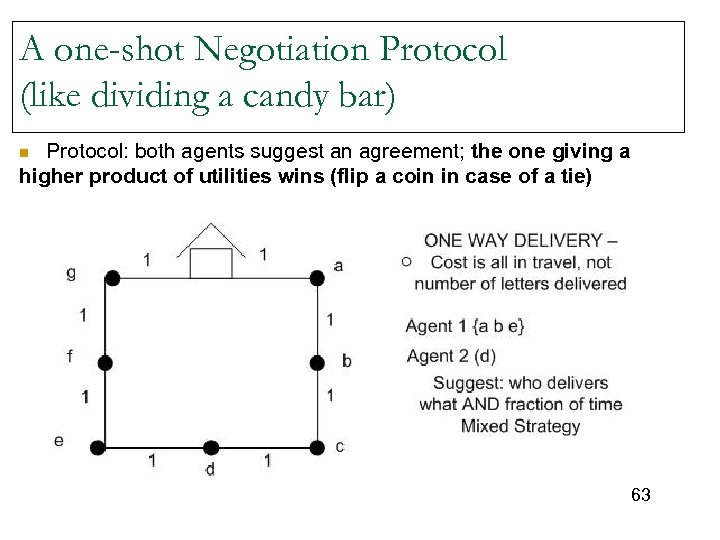A one-shot Negotiation Protocol (like dividing a candy bar) Protocol: both agents suggest an agreement; the one giving a higher product of utilities wins (flip a coin in case of a tie) n 63

A one-shot Negotiation Protocol (like dividing a candy bar) Protocol: both agents suggest an agreement; the one giving a higher product of utilities wins (flip a coin in case of a tie) n Obvious strategy: amongst the set of agreements with maximal product of utilities, propose the one that is best for you n Properties: This mechanism is: – efficient: outcomes have maximal Nash product and are Pareto optimal (like MCP with Zeuthen Strategy) – stable: no agent has an incentive to deviate from the strategy (like MCP with extended Zeuthen Strategy) n In addition, the one-shot protocol is also: – simple: only one round is required n But why should anyone accept to use such a protocol? (There is no motivation to be less than fair. ) n 64

Recap: How did we get to this point? Both agents making several small concessions until an agreement is reached is the most intuitive approach to one-to-one negotiation. n n The Monotonic Concession Protocol (MCP) is a straightforward formalization of the above intuition. Both propose at every round. n The Zeuthen Strategy is also motivated by intuition (“willingness to risk conflict”) and constitutes a stable and (almost) efficient strategy for the MCP. The one-shot protocol (together with the obvious strategy) produces similar outcomes as MCP/Zeuthen, but it is a much simpler mechanism. n 65

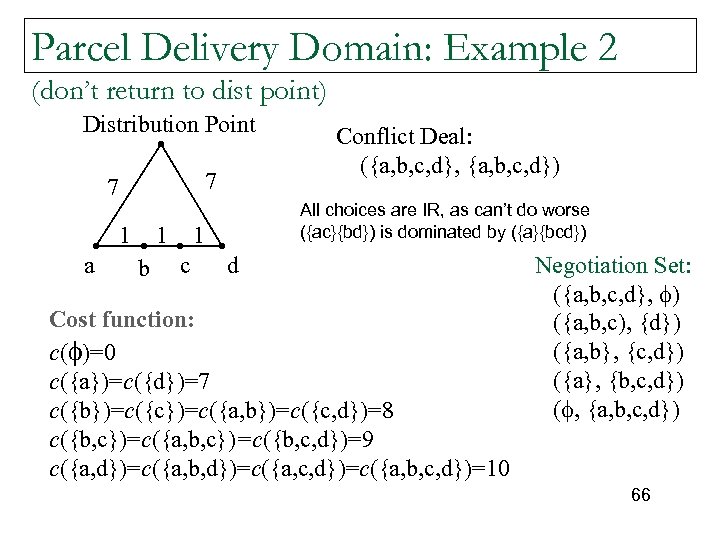Parcel Delivery Domain: Example 2 (don’t return to dist point) Distribution Point 7 7 1 a 1 b All choices are IR, as can’t do worse ({ac}{bd}) is dominated by ({a}{bcd}) 1 c Conflict Deal: ({a, b, c, d}, {a, b, c, d}) d Cost function: c( )=0 c({a})=c({d})=7 c({b})=c({c})=c({a, b})=c({c, d})=8 c({b, c})=c({a, b, c})=c({b, c, d})=9 c({a, d})=c({a, b, d})=c({a, c, d})=c({a, b, c, d})=10 Negotiation Set: ({a, b, c, d}, ) ({a, b, c), {d}) ({a, b}, {c, d}) ({a}, {b, c, d}) ( , {a, b, c, d}) 66

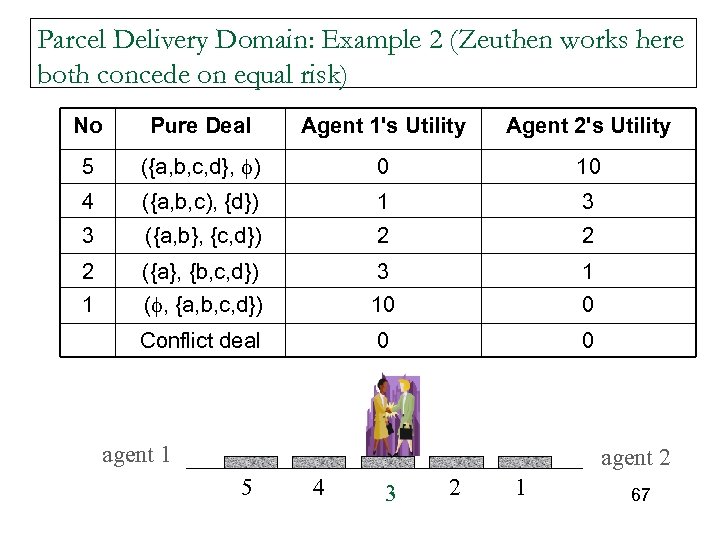Parcel Delivery Domain: Example 2 (Zeuthen works here both concede on equal risk) No Pure Deal Agent 1's Utility Agent 2's Utility 5 ({a, b, c, d}, ) 0 10 4 ({a, b, c), {d}) 1 3 3 ({a, b}, {c, d}) 2 2 2 ({a}, {b, c, d}) 3 1 1 ( , {a, b, c, d}) 10 0 Conflict deal 0 0 agent 1 agent 2 5 4 3 2 1 67

What bothers you about the previous agreement? n n Decide to both get (2, 2) utility, rather than the expected utility of (0, 10) for another choice. Is there a solution? Fair versus higher global utility. Restrictions of this method (no promises for future or sharing of utility) 68

State Oriented Domain n n Goals are acceptable final states (superset of TOD) Have side effects - agent doing one action might hinder or help another agent. Example in blocks world, on(white, gray) has side effect of clear(black). Negotiation : develop joint plans (what they each do) and schedules for the agents, to help and not hinder other agents Example – Slotted blocks world -blocks cannot go anywhere on table – only in slots (restricted resource) Note how this simple change (slots) makes it so two workers get in each other’s way even if goals are unrelated. 69

Assumptions of SOD u u u Agents will maximize expected utility (will prefer 51% chance of getting $100 than a sure $50) Agent cannot commit himself (as part of current negotiation) to behavior in future negotiation. No explicit utility transfer (no “money” that can be used to compensate one agent for a disadvantageous agreement) Interagent comparison of utility: common utility units Symmetric abilities (all can perform tasks, and cost is same regardless of agent performing) Binding commitments 70

Achievement of Final State n n n Goal of each agent is represented as a set of states that they would be happy with. Looking for a state in intersection of goals Possibilities: q (GREAT) Both can be achieved, at gain to both (e. g. travel to same location and split cost) q (IMPOSSIBLE) Goals may contradict, so no mutually acceptable state (e. g. , both need a car) q (NEED ALT) Can find common state, but perhaps it cannot be reached with the primitive operations in the domain (could both travel together, but may need to know how to pickup another) q (NOT WORTH IT) Might be a reachable state which satisfies both, but may be too expensive – unwilling to expend effort (i. e. , we could save a bit if we car-pooled, but is too complicated for so little gain). 71

Examples: Cooperative Each is helped by joint plan n n Slotted blocks world: initially white block is at 1 and black block at 2. Agent 1 wants black in 1. Agent 2 wants white in 2. (Both goals are compatible. ) Assume pick up is cost 1 and set down is one. Mutually beneficial – each can pick up at the same time, costing each 2 – Win – as didn’t have to move other block out of the way! If done by one, cost would be four – so utility to each is 2. 72

Examples: Compromise Both succeed, but worse for both than if other agent gone n n Slotted blocks world: initially white block is at 1 and black block at 2, two gray blocks at 3. Agent 1 wants black in 1, but not on table. Agent 2 wants white in 2, but not directly on table. Alone, agent 1 could just pick up black and place on white. Similarly, for agent 2. But would undo others goal. But together, all blocks must be picked up and put down. Best plan: one agent picks up black, while other agent rearranges (cost 6 for one, 2 for other) Can both be happy, but unequal roles. 73

Example: conflict n n n I want black on white (in slot 1) You want white on black (in slot 1) Can’t both win. Could flip a coin to decide who wins. Better than both losing. Weightings on coin needn’t be 50 -50. May make sense to have person with highest worth get his way – as utility is greater. (Would accomplish his goal alone) Efficient but not fair? What if we could transfer half of the gained utility to the other agent? This is not normally allowed, but could work out well. 74

Negotiation Domains: Worth-oriented n ”Domains where agents assign a worth to each potential state (of the environment), which captures its desirability for the agent”, (Rosenschein & Zlotkin, 1994) n agent’s goal is to bring about the state of the environment with highest value n we assume that the collection of agents have available a set of joint plans – a joint plan is executed by several different agents n Note – not ”all or nothing” – but how close you got to goal. 75

Worth Oriented Domain n n Rates the acceptability of final states Allows partially completed goals Negotiation : a joint plan, schedules, and goal relaxation. May reach a state that might be a little worse that the ultimate objective Example – Multi-agent Tile world (like airport shuttle) – isn’t just a specific state, but the value of work accomplished 76

How can we calculate Utility? n Weighting each attribute q n Rating/ranking each attribute q n Utility = {Price*60 + quality*15 + support*25} Price : 1, quality 2, support 3 Using constraints on an attribute q q Price[5, 100], quality[0 -10], support[1 -5] Try to find the pareto optimum 77

What if choices don’t benefit others fairly? n n Suppose there are two states that satisfy both agents. State 1: one has a utility of 6 for one agent and 3 for the other. State 2: utility of both agents 4. State 1 is better (overall), but state 2 is more equal. How can we get cooperation (as why should one agent agree to do more)? 78

Mixed Deal n n If = (J 1, J 2: p) is a deal, then utili( ) = p*util(J)i + (1 -p)*util(J)k where k is i’s opponent -the role i plays with (1 -p) probability An “all or nothing” form of a mixed deal simply means one set of tasks is everything. 79

Parcel Delivery Domain (assuming noreturn) Distribution Point 1 city a 1 2 city b Cost function: c( )=0 c({a})=1 c({b})=1 c({a, b)}=3 Utility for agent 1 (org {a}): 1. Utility 1({a}, {b}) = 0 2. Utility 1({b}, {a}) = 0 Utility for agent 2 (org {ab}): 1. Utility 2({a}, {b}) = 2 2. Utility 2({b}, {a}) = 2 3. Utility 1({a, b}, ) = -2 3. Utility 2({a, b}, ) = 3 4. Utility 1( , {a, b}) = 1 … 4. Utility 2( , {a, b}) = 0 … 80

At seats… n n n For the parcel delivery example above, show what a mixed deal does for the following deals: 1. deal “ 1”, each does one 2. deal “ 3”, all or nothing (notice a “pure” deal 3 is not even individually rational) 81

Consider deal 3 with probability n n n n ({}, {ab}): p means agent 1 does {} with p probabilty and {ab} with (1 -p) probabilty. What should p be to be fair to both (equal utility) (1 -p)(-2) + p 1 = utility for agent 1 (1 -p)(3) + p 0 = utility for agent 2 (1 -p)(-2) + p 1= (1 -p)(3) + p 0 -2+2 p+p = 3 -3 p => p=5/6 If agent 1 does no deliveries 5/6 of the time, it is fair. 82

Try again with other choice in negotiation (Deal 1) Utility 1({a}, {b}) = 0 n n n ({a}, {b}): p means agent 1 does {a} with p probabilty and {b} with (1 -p) probabilty. What should p be to be fair to both (equal utility) (1 -p)(0) + p 0 = utility for agent 1 (1 -p)(2) + p 2 = utility for agent 2 0=2 no solution Can you see why we can’t use a p to make this fair? 83

Incomplete Information n n Don’t know tasks of others in TOD. Solution q q n Exchange missing information Penalty for lie Possible lies (notice: reduce possibilities in order to be able to solve) q False information n n Hiding letters (don’t admit part of your job) Lie about letters (claim work that isn’t required) q q q decoy – produce if needed phantom – can’t produce, caught in lie Not carry out a commitment 84

Subadditive Task Oriented Domain Cost of whole is ≤ cost of parts n n for finite X, Y in T, c(X U Y) <= c(X) + c(Y)). Example of subadditive: q Deliver to one, saves distance to other (in a tree arrangement) Example of subadditive TOD (= rather than <) q deliver in opposite directions –doing both saves nothing Not subadditive: doing both actually costs more than the sum of the pieces. Say electrical power costs, where I get above a threshold and have to buy new equipment. 85

Decoy task n We call producible phantom tasks decoy tasks (no risk of being discovered). Only unproducible phantom tasks are called phantom tasks. n Example: Need to pick something up at store. (Can think of something for them to pick up, but if you are the one assigned, you won’t bother to make the trip. ) Need to deliver empty letter (no good, but deliverer won’t discover lie) n 86

Incentive compatible Mechanism Are the rules (in terms of allowable deals) we establish sufficient to produce truth telling? n n n L there exists a beneficial lie in some encounter T There exists no beneficial lie. T/P Truth is dominant if the penalty for lying is stiff enough. Example indicates a case where lying helps. Can you see it? Who lies? What is lie? 87

Explanation of arrow n If it is never beneficial in a mixed deal encounter to use a phantom lie (with penalties), then it is certainly never beneficial to do so in an all-or-nothing mixed deal encounter (which is just a subset of the mixed deal encounters). 88

Concave Task Oriented Domain n n We have 2 tasks X and Y, where X is a subset of Y Another set of task Z is introduced q c(YU Z) –c(Y) ≤c(XU Z) –c(X) 89

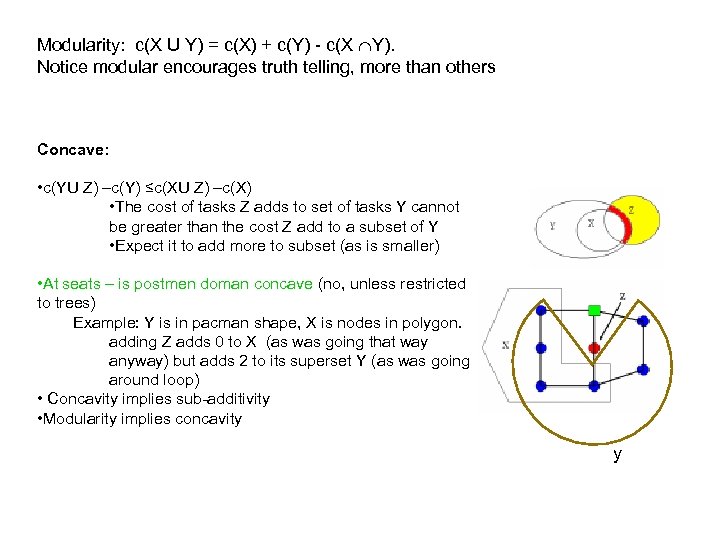Modularity: c(X U Y) = c(X) + c(Y) - c(X Y). Notice modular encourages truth telling, more than others Concave: • c(YU Z) –c(Y) ≤c(XU Z) –c(X) • The cost of tasks Z adds to set of tasks Y cannot be greater than the cost Z add to a subset of Y • Expect it to add more to subset (as is smaller) • At seats – is postmen doman concave (no, unless restricted to trees) Example: Y is in pacman shape, X is nodes in polygon. adding Z adds 0 to X (as was going that way anyway) but adds 2 to its superset Y (as was going around loop) • Concavity implies sub-additivity • Modularity implies concavity y

Explanation of Previous Chart n n n Arrows show reasons we know this fact (diagonal arrows are between domains). For example, What is true of a phantom task, may be true for a decoy task in same domain as a phantom is just a decoy task we don’t have to create. Similarly, what is true for a mixed deal may be true for an all or nothing deal (in the same domain) as a mixed deal is an all or nothing deal where one choice is empty. The direction of the relationship may depend on truth (never helps) or lie (sometimes helps). The relationships can also go between domains as subadditive is a superclass of concave and a super class of modular. 91

Modular TOD n n c(X U Y) = c(X) + c(Y) - c(X Y). Notice modular encourages truth telling, more than others 92

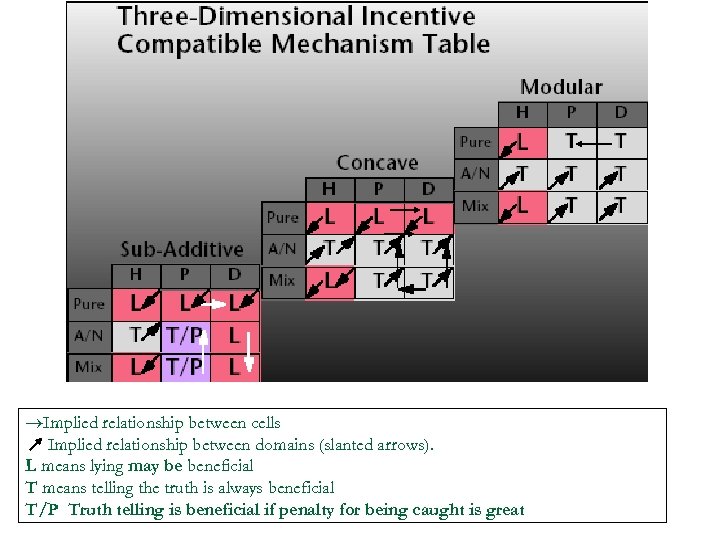Implied relationship between cells Implied relationship between domains (slanted arrows). L means lying may be beneficial T means telling the truth is always beneficial T/P Truth telling is beneficial if penalty for being caught is great 93

Attributes-Modularity n n c(XU Y) = c(X) + c(Y) –c(X∩Y) • The cost of the combination of 2 sets of tasks is exactly the sum of their individual costs minus the cost of their intersection Only Fax Domain is modular (as costs are independent) Modularity implies concavity 94

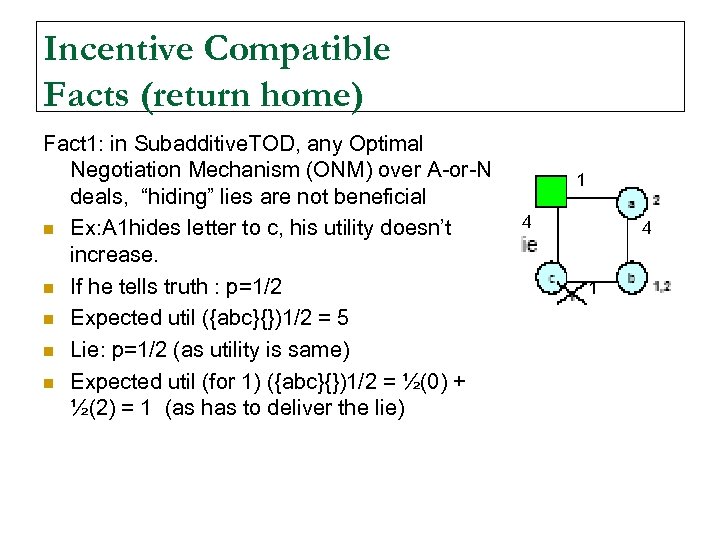Incentive Compatible Facts (return home) Fact 1: in Subadditive. TOD, any Optimal Negotiation Mechanism (ONM) over A-or-N deals, “hiding” lies are not beneficial n Ex: A 1 hides letter to c, his utility doesn’t increase. n If he tells truth : p=1/2 n Expected util ({abc}{})1/2 = 5 n Lie: p=1/2 (as utility is same) n Expected util (for 1) ({abc}{})1/2 = ½(0) + ½(2) = 1 (as has to deliver the lie) 1 4 4 1

n n n Fact 2 in Subadditive. TOD, any ONM over Mixed deals, every “phantom” lie has a positive probability of being discovered. (as if other person delivers phantom, you are found out) Fact 3 in Concave TOD, any ONM over Mixed deals, no “decoy” lie is beneficial. (as less increased cost is assumed so probabilities would be assigned to reflect the assumed extra work) Fact 4 in Modular TOD, any ONM over Pure deals, no “decoy” lie is beneficial. (modular tends to add exact cost – hard to win) 96

Fact 4 Modular, all or nothing, decoy 1 Under Lie – benefits are shown Under Truth, p would be 1/2 If we assign p ({ebc}, ) p agent 1 utility -2*p + 6(1 -p) Agent 2 (under lie) 8 p+0(1 -p) -2*p + 6(1 -p)= 8 p+0(1 -p) -8 p+6 = 8 p p=6/16 (so 2 is worse off) 2 eb Both deliver to e and b. Suppose agent 2 lies about having a delivery to c. U(1) 0 ebc 0 0 ebc -2 8 6 ebc 0 0 6 U(2) Seems U(2) (act)

n n n Fact 5: in Concave TOD, any ONM over Pure deals, “Phantom” lies can be beneficial. Example from next slide: A 1 creates Phantom letter at node c, his utility has risen from 3 to 4 Truth: p = ½ so utility for agent 1 is ({a}{b}) ½ = ½(4) + ½(2) = 3 Lie: ({bc}{a}) is logical division as no percent Util for agent 1 is 6 (org cost) – 2(deal cost) = 4 98

n n n n n Fact 6: in Subadditive. TOD, any ONM over A-or-N deals, “Decoy” lies can be beneficial (not harmful). (as it changes the probability. If you deliver, I make you deliver to h) Ex 2 (from next slide): A 1 lies with decoy letter to h (trying to make agent 2 think picking up bc is worse for agent 1 than it is), his utility has rised from 1. 5 to 1. 72. (If I deliver, I don’t deliver h) If tells truth, p (of agent 1 delivering all) = 9/14 as p(-1) + (1 -p)6 = p(4) + (1 -p)(-3) 14 p=9 If invents task h, p=11/18 as p(-3) + (1 -p)6 = p(4) + (1 -p)(-5) Utility(p=9/14) is p(-1) + (1 -p)6 = -9/14 +30/14 = 21/14 = 1. 5 Utility(p=11/18) is p(-1) + (1 -p)6 = -11/18 +42/18 = 31/18 = 1. 72 SO – lying helped! 99

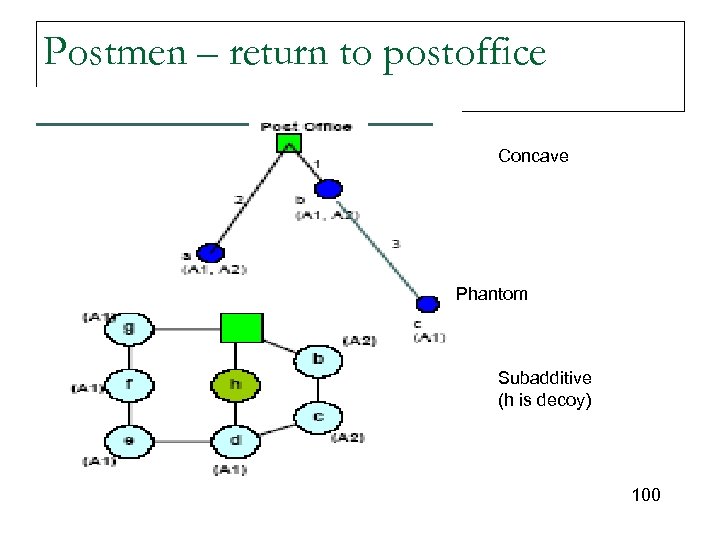Postmen – return to postoffice Concave Phantom Subadditive (h is decoy) 100

n n n Fact 7: in Modular TOD, any ONM over Pure deals, “Hide” lie can be beneficial. (as you think I have less, so increase load will cost more than it realy does) Ex 3 (from next slide): A 1 hides his letter node b ({e}{b}) = utility for A 1 (under lie) is 0 = utility for A 2 (under lie) is 4 UNFAIR (under lie) ({b}{e}) = utility for A 1 (under lie) is 2 = utility for A 2 (under lie) is 2 So I get sent to b, but I really needed to go there anyway, so my utility is actually 4. (as I don’t go to e) 101

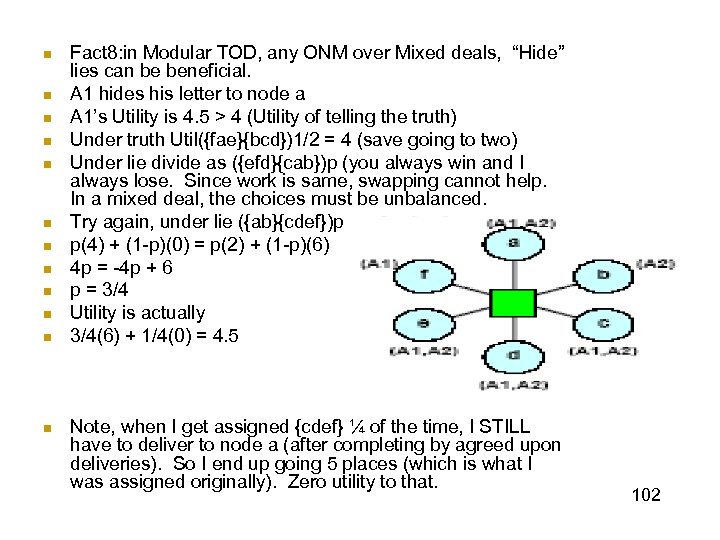n n n Fact 8: in Modular TOD, any ONM over Mixed deals, “Hide” lies can be beneficial. A 1 hides his letter to node a A 1’s Utility is 4. 5 > 4 (Utility of telling the truth) Under truth Util({fae}{bcd})1/2 = 4 (save going to two) Under lie divide as ({efd}{cab})p (you always win and I always lose. Since work is same, swapping cannot help. In a mixed deal, the choices must be unbalanced. Try again, under lie ({ab}{cdef})p p(4) + (1 -p)(0) = p(2) + (1 -p)(6) 4 p = -4 p + 6 p = 3/4 Utility is actually 3/4(6) + 1/4(0) = 4. 5 Note, when I get assigned {cdef} ¼ of the time, I STILL have to deliver to node a (after completing by agreed upon deliveries). So I end up going 5 places (which is what I was assigned originally). Zero utility to that. 102

Conclusion q q In order to use Negotiation Protocols, it is necessary to know when protocols are appropriate TOD’s cover an important set of Multi-agent interaction 103

MAS Compromise: Negotiation process for conflicting n Identify potential interactions goals n Modify intentions to avoid harmful interactions or create cooperative situations n Techniques required q q q Representing and maintaining belief models Reasoning about other agents beliefs Influencing other agents intentions and beliefs 104

PERSUADER – case study n n n Program to resolve problems in labor relations domain Agents q Company q Union q Mediator Tasks q Generation of proposal q Generation of counter proposal based on feedback from dissenting party q Persuasive argumentation 105

Negotiation Methods: Case Based Reasoning Uses past negotiation experiences as guides to present n n negotiation (like in court of law – cite previous decisions) Process q Retrieve appropriate precedent cases from memory q Select the most appropriate case q Construct an appropriate solution q Evaluate solution for applicability to current case q Modify the solution appropriately 106

Case Based Reasoning n n Cases organized and retrieved according to conceptual similarities. Advantages q Minimizes need for information exchange q Avoids problems by reasoning from past failures. Intentional reminding. q Repair for past failure is used. Reduces computation. 107

Negotiation Methods: Preference Analysis n n n From scratch planning method Based on multi attribute utility theory Gets a overall utility curve out of individual ones. Expresses the tradeoffs an agent is willing to make. Property of the proposed compromise q Maximizes joint payoff q Minimizes payoff difference 108

Persuasive argumentation n n Argumentation goals q Ways that an agent’s beliefs and behaviors can be affected by an argument Increasing payoff q Change importance attached to an issue q Changing utility value of an issue 109

Narrowing differences n n Gets feedback from rejecting party q Objectionable issues q Reason for rejection q Importance attached to issues Increases payoff of rejecting party by greater amount than reducing payoff for agreed parties. 110

Experiments n n n Without Memory – 30% more proposals Without argumentation – fewer proposals and better solutions No failure avoidance – more proposals with objections No preference analysis – Oscillatory condition No feedback – communication overhead increased by 23% 111

Multiple Attribute: Example 2 agents are trying to set up a meeting. The first agent wishes to meet later in the day while the second wishes to meet earlier in the day. Both prefer today to tomorrow. While the first agent assigns highest worth to a meeting at 16: 00 hrs, s/he also assigns progressively smaller worths to a meeting at 15: 00 hrs, 14: 00 hrs…. By showing flexibility and accepting a sub-optimal time, an agent can accept a lower worth which may have other payoffs, (e. g. reduced travel costs). 100 Ref: Rosenschein & Zlotkin, 1994 Worth function for first agent 0 9 12 16 112

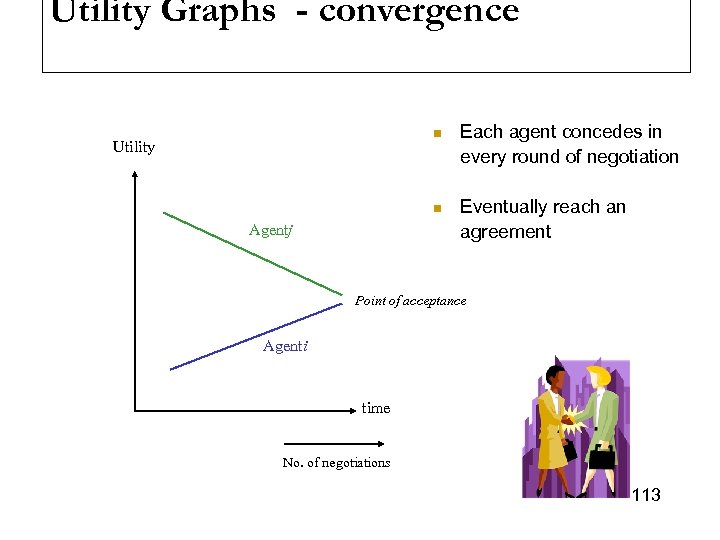Utility Graphs - convergence n n Utility Agentj Each agent concedes in every round of negotiation Eventually reach an agreement Point of acceptance Agenti time No. of negotiations 113

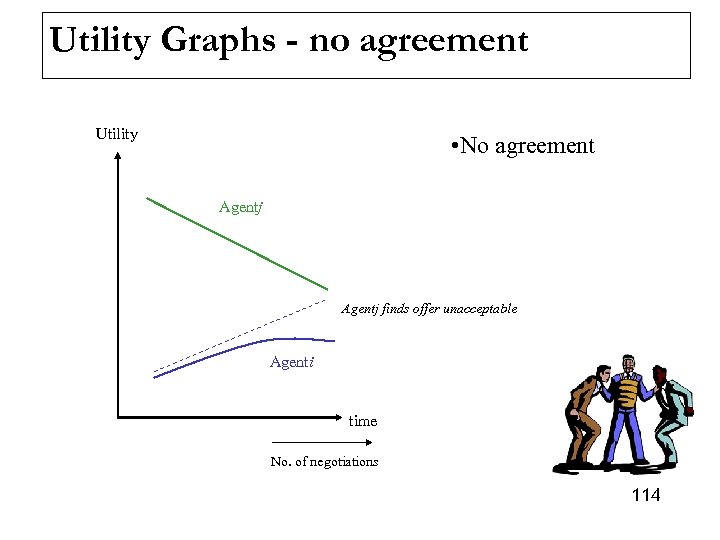Utility Graphs - no agreement Utility • No agreement Agentj finds offer unacceptable Agenti time No. of negotiations 114

Argumentation n The process of attempting to convince others of something. n Why argument-based negotiations: game-theoretic approaches have limitations n Positions cannot be justified – Why did the agent pay so much for the car? n Positions cannot be changed – Initially I wanted a car with a sun roof. But I changed preference during the buying process. 115

4 modes of argument (Gilbert 1994): n 1. Logical - ”If you accept A and accept A implies B, then you must accept that B” 2. Emotional - ”How would you feel if it happened to you? ” 3. Visceral - participant stamps their feet and show the strength of their feelings 4. Kisceral - Appeals to the intuitive – doesn’t this seem reasonable 116

Logic Based Argumentation n Basic form of argumentation Database ├ (Sentence, Grounds) Where Database: is a (possibly inconsistent) set of logical formulae Sentence is a logical formula know as the conclusion Grounds is a set of logical formula grounds database sentence can be proved from grounds (we give reason for our conclusions) 117

Attacking Arguments Milk is good for you n Cheese is made from milk n Cheese is good for you Two fundamental kinds of attack: n Undercut (invalidate premise): milk isn’t good for you if fatty n Rebut (contradict conclusion): Cheese is bad for bones n 118

Attacking arguments n Derived notions of attack used in Literature: q A attacks B = A u B or A r B q A defeats B = A u B or (A r B and not B u A) q A strongly attacks B = A a B and not B u A q A strongly undercuts B = A u B and not B u A 119

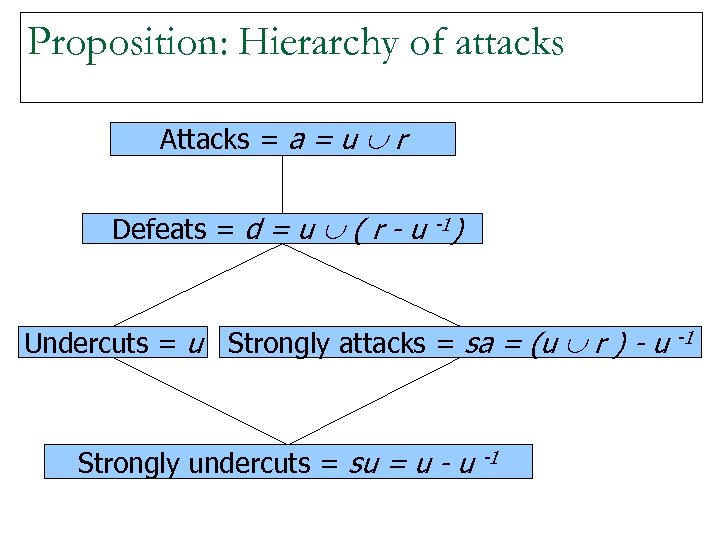Proposition: Hierarchy of attacks Attacks = a = u r Defeats = d = u ( r - u -1) Undercuts = u Strongly attacks = sa = (u r ) - u Strongly undercuts = su = u -1 -1

Abstract Argumentation Concerned with the overall structure of the argument (rather than internals of arguments) n Write x y indicates q “argument x attacks argument y” q “x is a counterexample of y” q “x is an attacker of y” where we are not actually concerned as to what x, y are n An abstract argument system is a collection or arguments together with a relation “ ” saying what attacks what n An argument is out if it has an undefeated attacker, and in if all its attackers are defeated. n Assumption – true unless proven false n 121

Admissible Arguments – mutually defensiblex is attacked if no member attacks y 1. argument 2. 3. 4. and y x argument x is acceptable if every attacker of x is attacked argument set is conflict free if none attack each other set is admissible if conflict free and each argument is acceptable (any attackers are attacked) 122

a c b Which sets of arguments can be true? c is always attacked. d is always acceptable d

An Example Abstract Argument System 124