-RC Circuits -Household Safety AP Physics C Mrs

-RC Circuits -Household Safety AP Physics C Mrs. Coyle

RC Circuits • Resistors and Capacitors in the circuit.

Two Situations for RC Circuits Steady State Variable Current • Occurs when the capacitor is fully charged • There is no current in the branch of the fully charged capacitor (it acts as an open circuit) • The current in the other braches is constant (steady state) • While the capacitor is charging or discharging

Charging a Capacitor in an RC Circuit • When the switch is closed, the capacitor starts to charge and the current is at maximum. • The current decreases as the capacitor continues to charge until it reaches its maximum charge (Q = CVc) • The potential difference increases until a maximum Vc. • Once the capacitor is fully charged, the current is zero. Vc

Steady State RC Circuit • When the capacitor is fully charged no current flows through the branch it is in. • The capacitor has its maximum voltage. • Sign convention for the capacitor voltage is the same as a battery: Vc is (+) when we traverse from the (–) to the (+) plate of the capacitor (low potential to high potential) -| | +

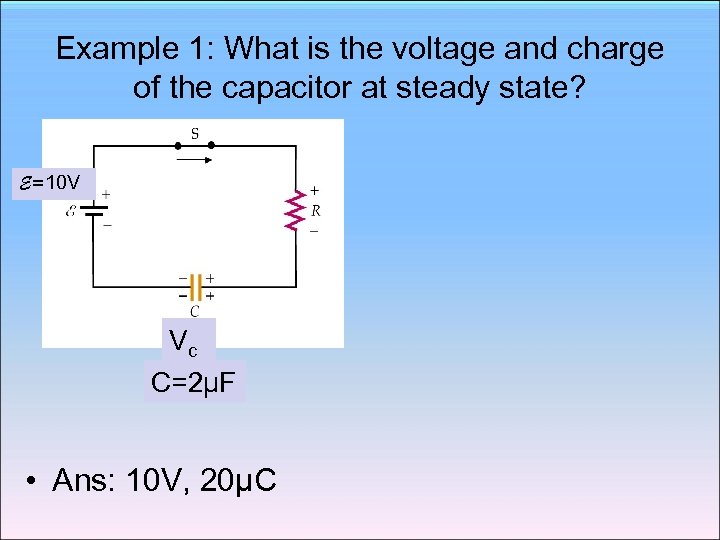Example 1: What is the voltage and charge of the capacitor at steady state? E=10 V Vc C=2μF • Ans: 10 V, 20μC

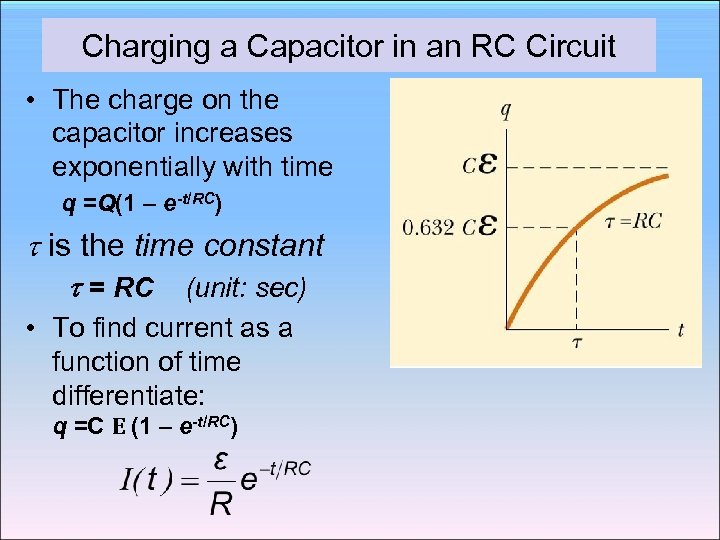Charging a Capacitor in an RC Circuit • The charge on the capacitor increases exponentially with time q =Q(1 – e-t/RC) is the time constant = RC (unit: sec) • To find current as a function of time differentiate: q =C E (1 – e-t/RC)

Example 2 • Derive q =Q(1 – e-t/RC). • Hint: use Kirchhoff’ loop rule and substitute I=dq/dt

Time Constant and U • In a time t=RC then q=Q(1 -e-1)=0. 632 Q • The time constant represents the time required for the charge to increase from zero to 63. 2% of Q maximum. • The energy stored in the charged capacitor is U=½ Qe = ½ Ce 2

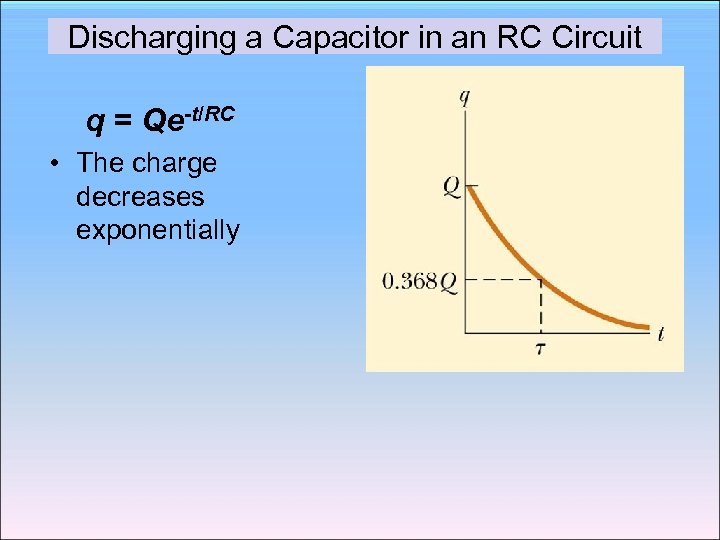Discharging a Capacitor in an RC Circuit q = Qe-t/RC • The charge decreases exponentially

Discharging a Capacitor in an RC Circuit • At t = = RC, q= Q e-1 = 0. 368 Qmax • In one time constant, the capacitor loses 63. 2% of its initial charge • Current:

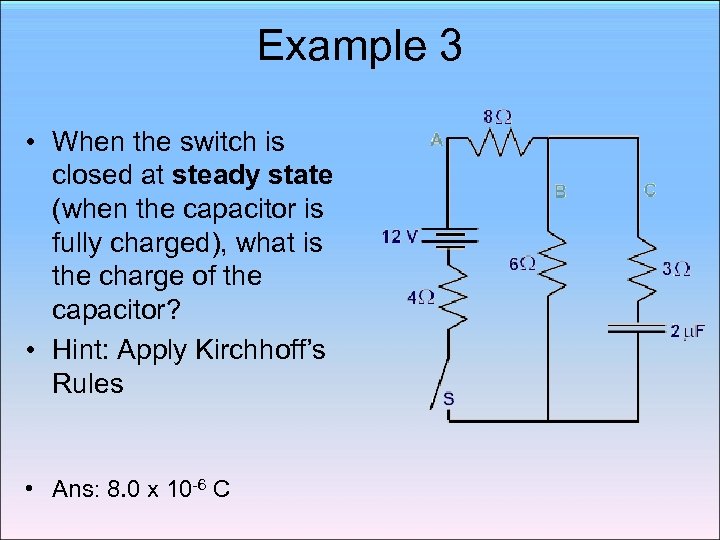Example 3 • When the switch is closed at steady state (when the capacitor is fully charged), what is the charge of the capacitor? • Hint: Apply Kirchhoff’s Rules • Ans: 8. 0 x 10 -6 C

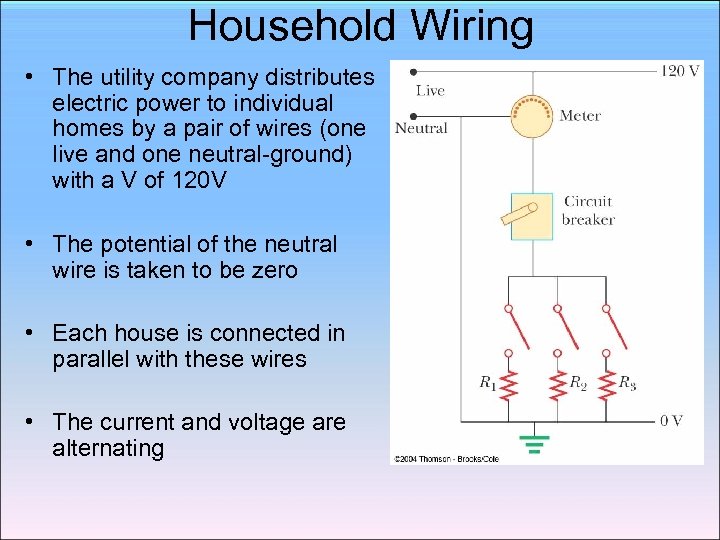Household Wiring • The utility company distributes electric power to individual homes by a pair of wires (one live and one neutral-ground) with a V of 120 V • The potential of the neutral wire is taken to be zero • Each house is connected in parallel with these wires • The current and voltage are alternating

Short Circuit • A short circuit occurs when almost zero resistance exists between two points at different potentials • This results in a very large current • In a household circuit, a circuit breaker will open the circuit in the case of an accidental short circuit – This prevents any damage

Effects of Various Currents • 5 m. A or less – can cause a sensation of shock – generally little or no damage • 10 m. A – muscles contract – may be unable to let go of a live wire • 100 m. A – if passing through the body for 1 second or less, can be fatal – paralyzes the respiratory muscles

Household Safety • Why should you not plug too many appliances in the same outlet? • What is the role of a circuit breaker? • Why should you not touch an electric appliance with wet hands? • What causes human injury current or voltage? • Why is grounding used?

More Effects • In some cases, currents of 1 A can produce serious burns – Sometimes these can be fatal burns • No contact with live wires is considered safe whenever the voltage is greater than 24 V

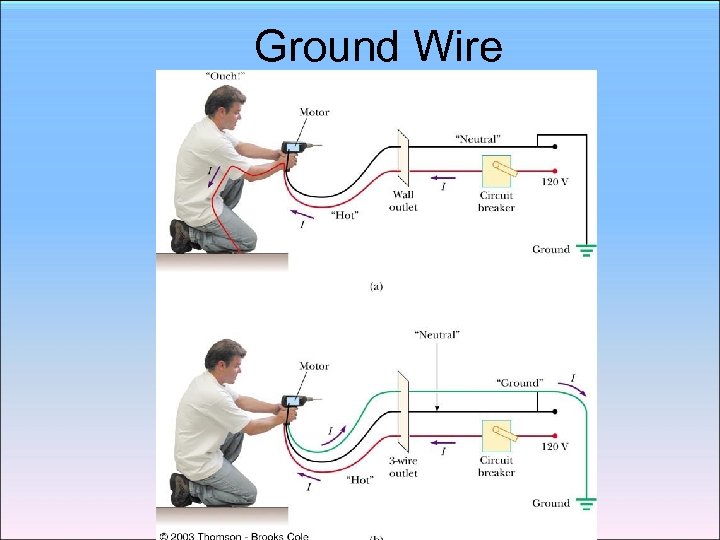Ground Wire

Ground-Fault Interrupters (GFI) • Special power outlets • Used in hazardous areas • Designed to protect people from electrical shock • Senses currents (of about 5 m. A or greater) leaking to ground • Shuts off the current when above this level