RBEs and MPCs in MSC.Nastran A Rip-Roarin’ Review


RBEs and MPCs in MSC.Nastran A Rip-Roarin’ Review of Rigid Elements

Slide 2 RBEs and MPCs Not necessarily “rigid” elements Working Definition: The motion of a DOF is dependent on the motion of at least one other DOF

Slide 3 Motion at one GRID drives another Simple Translation X motion of Green Grid drives X motion of Red Grid
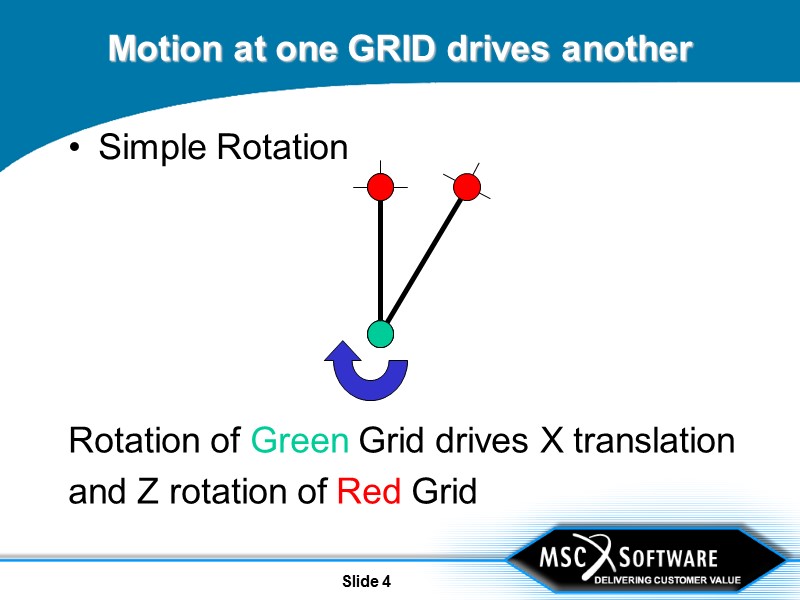
Slide 4 Motion at one GRID drives another Simple Rotation Rotation of Green Grid drives X translation and Z rotation of Red Grid

Slide 5 RBEs and MPCs The motion of a DOF is dependent on the motion of at least one other DOF Displacement, not elastic relationship Not dictated by stiffness, mass, or force Linear relationship Small displacement theory Dependent v. Independent DOFs Stiffness/mass/loads at dependent DOF transferred to independent DOF(s)
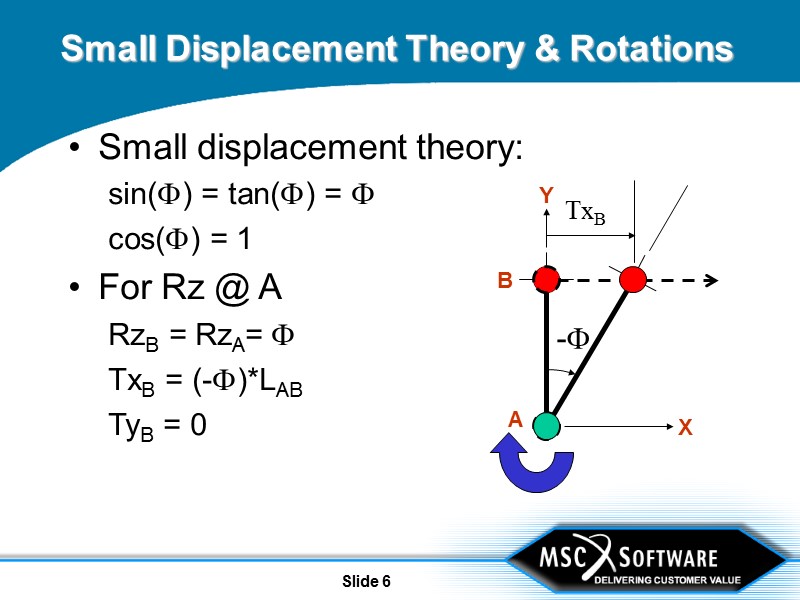
Slide 6 Small Displacement Theory & Rotations Small displacement theory: sin() = tan() = cos() = 1 For Rz @ A RzB = RzA= TxB = (-)*LAB TyB = 0 X Y A B - TxB

Slide 7 Geometry-based RBAR RBE2 Geometry- & User-input based RBE3 User-input based MPC Typical “Rigid” Elements in MSC.Nastran } Really-rigid “rigid” elements
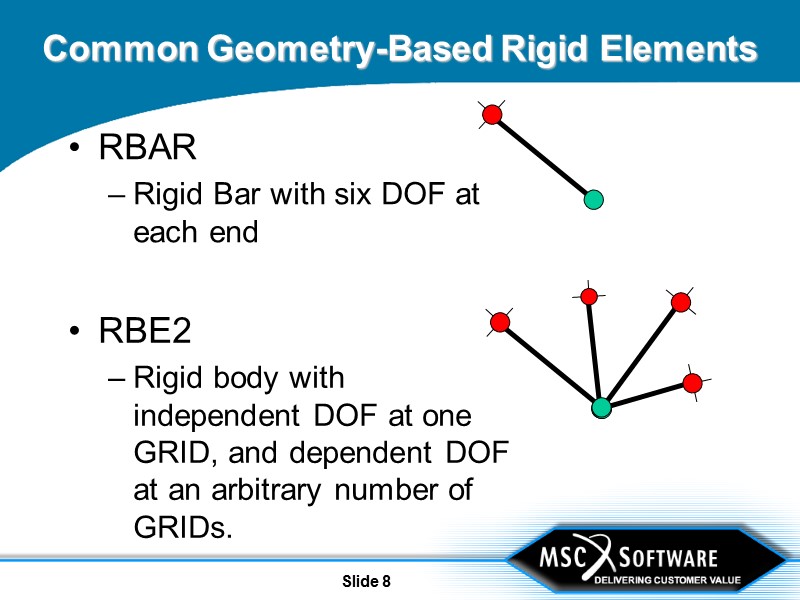
Slide 8 Common Geometry-Based Rigid Elements RBAR Rigid Bar with six DOF at each end RBE2 Rigid body with independent DOF at one GRID, and dependent DOF at an arbitrary number of GRIDs.
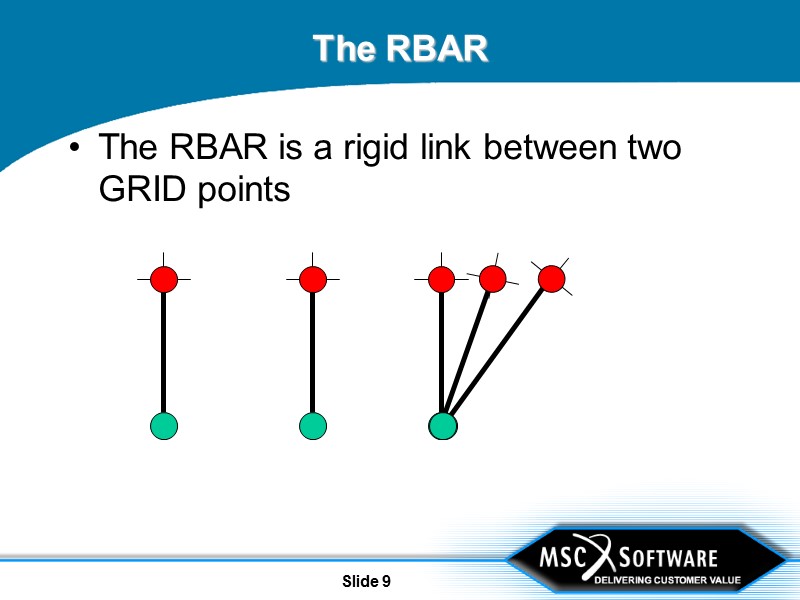
Slide 9 The RBAR The RBAR is a rigid link between two GRID points
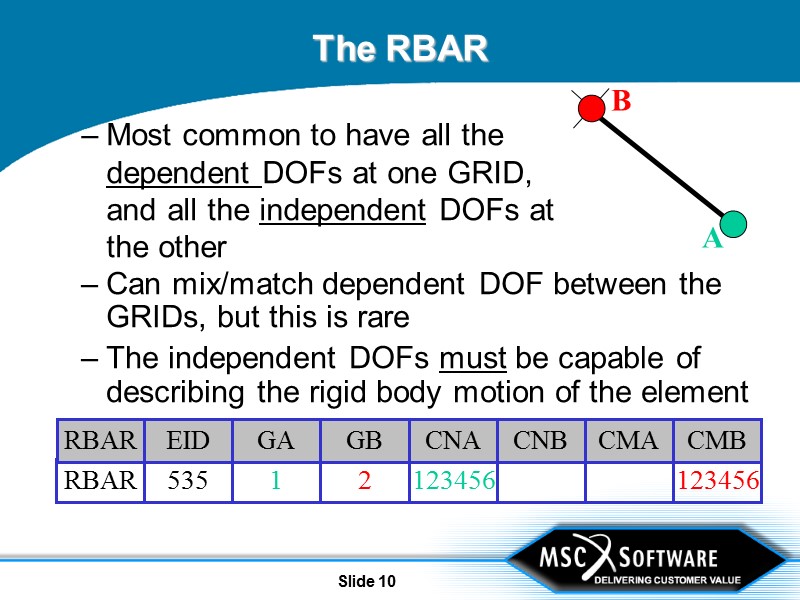
Slide 10 The RBAR Can mix/match dependent DOF between the GRIDs, but this is rare The independent DOFs must be capable of describing the rigid body motion of the element Most common to have all the dependent DOFs at one GRID, and all the independent DOFs at the other B A
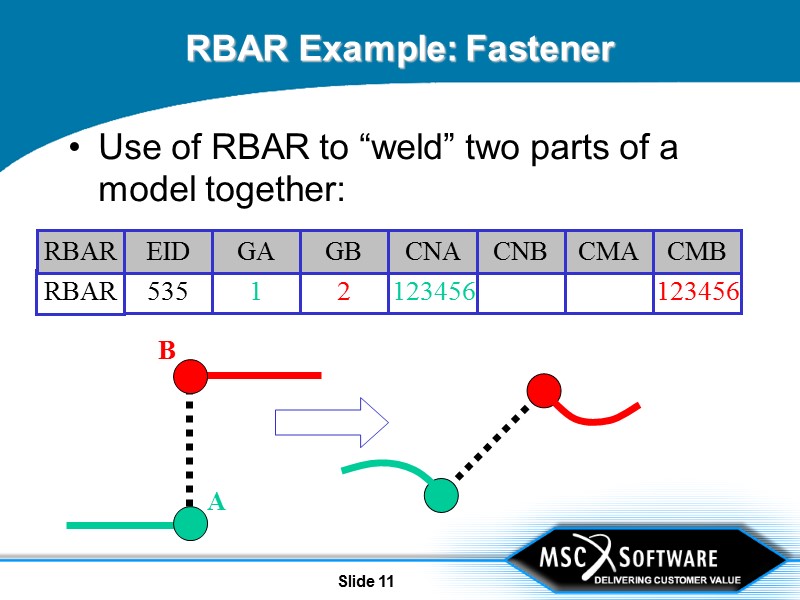
Slide 11 RBAR Example: Fastener Use of RBAR to “weld” two parts of a model together: B A
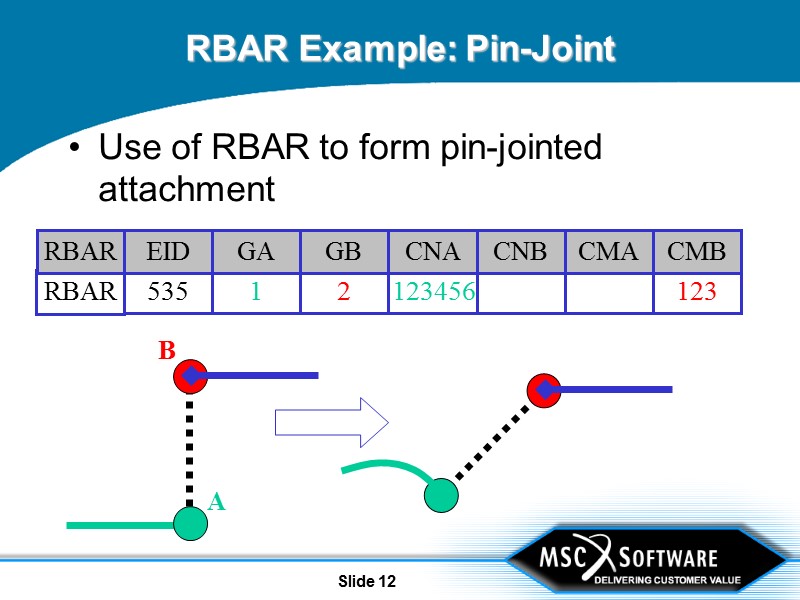
Slide 12 RBAR Example: Pin-Joint Use of RBAR to form pin-jointed attachment B A
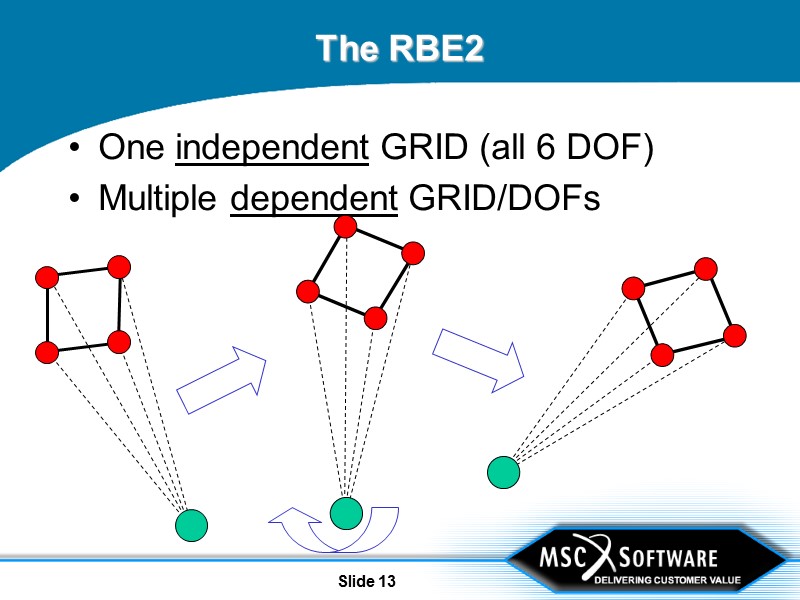
Slide 13 The RBE2 One independent GRID (all 6 DOF) Multiple dependent GRID/DOFs

Slide 14 RBE2 Example Rigidly “weld” multiple GRIDs to one other GRID:
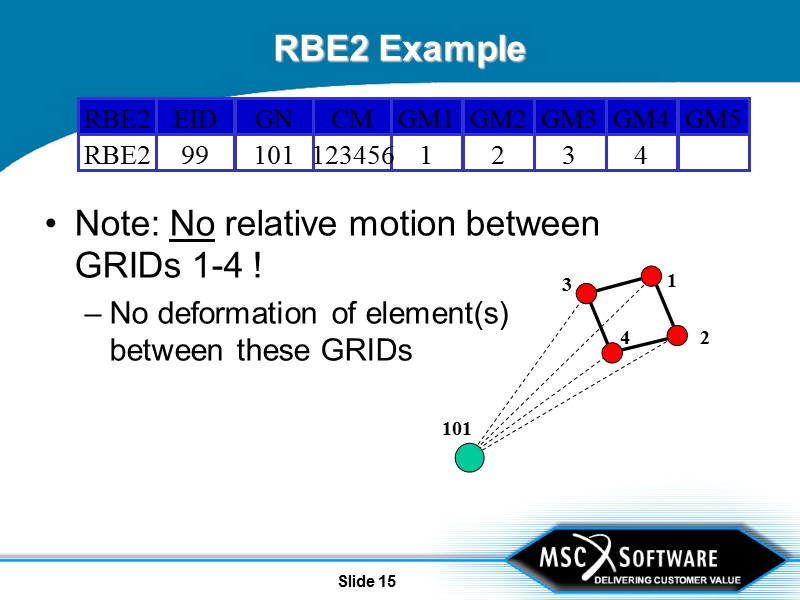
Slide 15 RBE2 Example Note: No relative motion between GRIDs 1-4 ! No deformation of element(s) between these GRIDs

Slide 16 Common RBE2/RBAR Uses RBE2 or RBAR between 2 GRIDs “Weld” 2 different parts together 6DOF connection “Bolt” 2 different parts together 3DOF connection RBE2 “Spider” or “wagon wheel” connections Large mass/base-drive connection

Slide 17 RBE3 Elements NOT a “rigid” element IS an interpolation element Does not add stiffness to the structure (if used correctly) Motion at a dependent GRID is the weighted average of the motion(s) at a set of master (independent) GRIDs
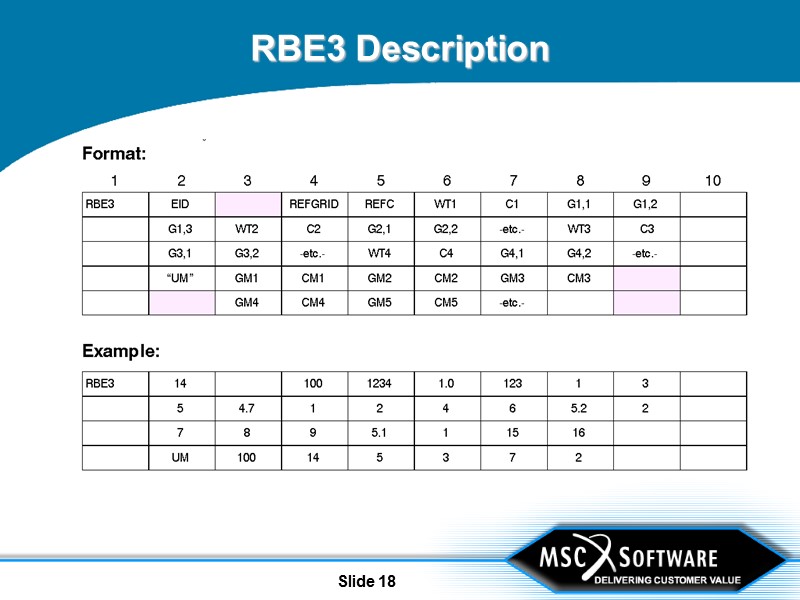
Slide 18 RBE3 Description

Slide 19 RBE3 Description By default, the reference grid DOF will be the dependent DOF Number of dependent DOF is equal to the number of DOF on the REFC field Dependent DOF cannot be SPC’d, OMITted, SUPORTed or be dependent on other RBE/MPC elements

Slide 20 U99 = (U1 + U2 + U3) / 3 3 * U99 = U1 + U2 + U3 -U1 = + U2 + U3 - 3 * U99 RBE3 Description UM fields can be used to move the dependent DOF away from the reference grid For Example (in 1-D):

Slide 21 RBE3 Is Not Rigid! RBE3 vs. RBE2 RBE3 allows warping and 3D effects In this example, RBE2 enforces beam theory (plane sections remain planar) RBE3 RBE2

Slide 22 RBE3: How it Works? Forces/moments applied at reference grid are distributed to the master grids in same manner as classical bolt pattern analysis Step 1: Applied loads are transferred to the CG of the weighted grid group using an equivalent Force/Moment Step 2: Applied loads at CG transferred to master grids according to each grid’s weighting factor

Slide 23 RBE3: How it Works? Step 1: Transform force/moment at reference grid to equivalent force/moment at weighted CG of master grids. MCG=MA+FA*e FCG=FA

Slide 24 RBE3: How it Works? Step 2: Move loads at CG to master grids according to their weighting values. Force at CG divided amongst master grids according to weighting factors Wi Moment at CG mapped as equivalent force couples on master grids according to weighting factors Wi
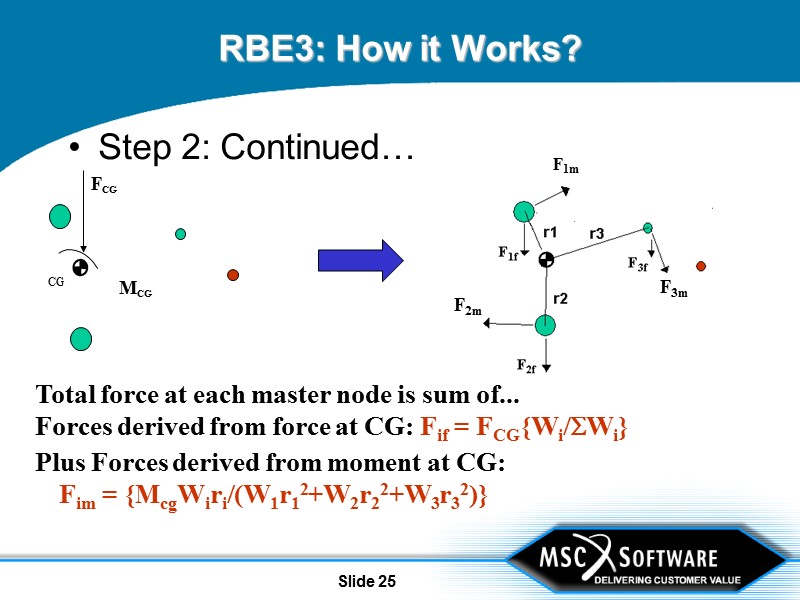
Slide 25 RBE3: How it Works? Step 2: Continued… Total force at each master node is sum of... Forces derived from force at CG: Fif = FCG{Wi/Wi} Plus Forces derived from moment at CG: Fim = {McgWiri/(W1r12+W2r22+W3r32)}

Slide 26 RBE3: How it Works? Masses on reference grid are smeared to the master grids similar to how forces are distributed Mass is distributed to the master grids according to their weighting factors Motion of reference mass results in inertial force that gets transferred to master grids Reference node inertial force is distributed in same manner as when static force is applied to the reference grid.

Slide 27 Example 1 RBE3 distribution of loads when force at reference grid at CG passes through CG of master grids

Slide 28 Example 1: Force Through CG Simply supported beam 10 elements, 11 nodes numbered 1 through 11 100 LB. Force in negative Y on reference grid 99

Slide 29 Example 1: Force Through CG Load through CG with uniform weighting factors results in uniform load distribution

Slide 30 Example 1: Force Through CG Comments… Since master grids are co-linear, the x rotation DOF is added so that master grids can determine all 6 rigid body motions, otherwise RBE3 would be singular

Slide 31 Example 2 How does the RBE3 distribute loads when force on reference grid does not pass through CG of master grids?

Slide 32 Example 2: Load not through CG The resulting force distribution is not intuitively obvious Note forces in the opposite direction on the left side of the beam. Upward loads on left side of beam result from moment caused by movement of applied load to the CG of master grids.

Slide 33 Example 3 Use of weighting factors to generate realistic load distribution: 100 LB. transverse load on 3D beam.

Slide 34 Example 3: Transverse Load on Beam If uniform weighting factors are used, the load is equally distributed to all grids.

Slide 35 Example 3: Transverse Load on Beam Displacement Contour The uniform load distribution results in too much transverse load in flanges causing them to droop.

Slide 36 Example 3: Transverse Load on Beam Assume quadratic distribution of load in web Assume thin flanges carry zero transverse load Master DOF 1235. DOF 5 added to make RY rigid body motion determinate

Slide 37 Displacements with quadratic weighting factors virtually equivalent to those from RBE2 (Beam Theory), but do not impose “plane sections remain planar” as does RBE2. Example 3: Transverse Load on Beam
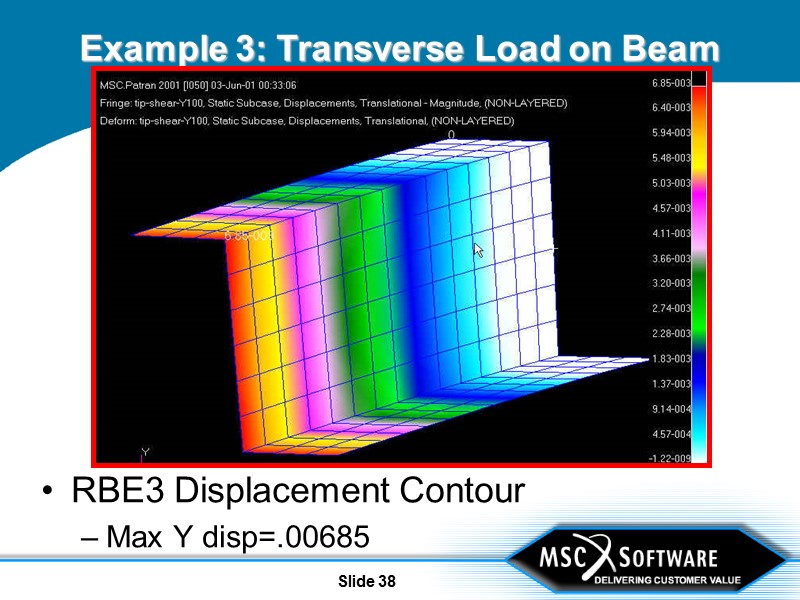
Slide 38 Example 3: Transverse Load on Beam RBE3 Displacement Contour Max Y disp=.00685

Slide 39 Example 3: Transverse Load on Beam RBE2 Displacement contour Max Y disp=.00685

Slide 40 Example 4 Use RBE3 to get “unconstrained” motion Cylinder under pressure Which Grid(s) do you pick to constrain out Rigid body motion, but still allow for free expansion due to pressure?

Slide 41 Example 4: Use RBE3 for Unconstrained Motion Solution: Use RBE3 Move dependent DOF from reference grid to selected master grids with UM option on RBE3 (otherwise, reference grid cannot be SPC’d) Apply SPC to reference grid

Slide 42 Example 4: Use RBE3 for Unconstrained Motion Since reference grid has 6 DOF, we must assign 6 “UM” DOF to a set of master grids Pick 3 points, forming a nice triangle for best numerical conditioning Select a total of 6 DOF over the three UM grids to determine the 6 rigid body motions of the RBE3 Note: “M” is the NASTRAN DOF set name for dependent DOF
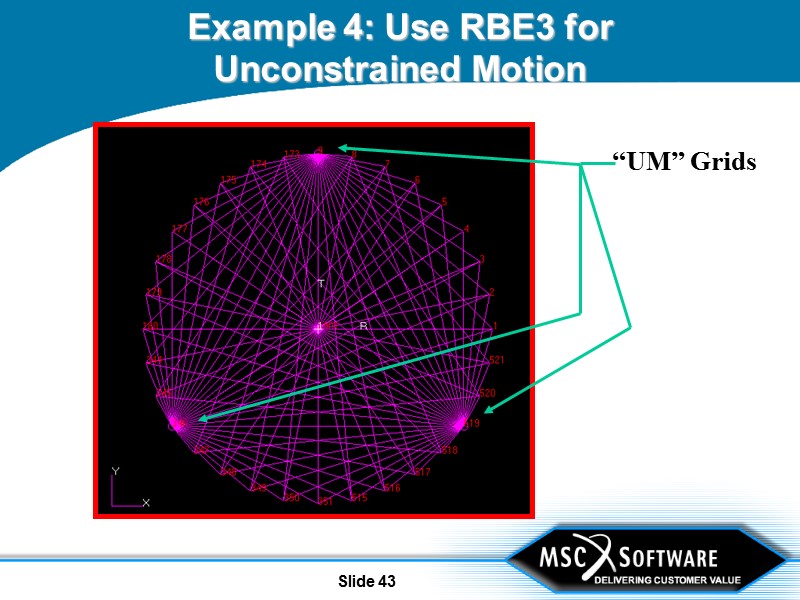
Slide 43 Example 4: Use RBE3 for Unconstrained Motion “UM” Grids

Slide 44 Example 4: Use RBE3 for Unconstrained Motion For circular geometry, it’s convenient to use a cylindrical coordinate system for the master grids. Put THETA and Z DOF in UM set for each of the three UM grids to determine RBE3 rigid body motion

Slide 45 Example 4: Use RBE3 for Unconstrained Motion Result is free expansion due to internal pressure. (note: poisson effect causes shortening)

Slide 46 Example 4: Use RBE3 for Unconstrained Motion Resulting MPC Forces are numeric zeroes verifying that no stiffness has been added.

Slide 47 Example 5 Connect 3D model to stick model 3D model with 7 psi internal pressure Use RBE3 instead of RBE2 so that 3D model can expand naturally at interface. RBE3 will also allow warping and other 3D effects at the interface.

Slide 48 Example 5: 3D to Stick Model Connection 120” diameter cylinder 7 psi internal pressure 10000 Lb. transverse load on stick model RBE3: Reference grid at center with 6 DOF, Master Grids with 3 translations

Slide 49 Example 5: 3D to Stick Model Connection

Slide 50 Example 5: 3D to Stick Model Connection Undeformed/Deformed plot shows continuity in motion of 3D and Beam model

Slide 51 Example 5: 3D to Stick Model Connection MPC forces at interface show effect of both the tip shear and interface moment.

Slide 52 Example 5: 3D to Stick Model Connection Shell outer fiber stresses at interface slightly higher than beam bending stresses 3D effects Shell model under internal pressure and not bound by beam theory assumptions

Slide 53 Example 6 Use RBE3 to see “beam” type modes from a complex model Sometimes it’s difficult to identify and describe modes of complex structures Solution: Connect complex structure down to centerline grids with RBE3. Connect centerline grids with PLOTELs

Slide 54 Example 6: Using RBE3 to Visualize “Beam” Modes Generic engine courtesy of Pratt & Whitney

Slide 55 Example 6: Using RBE3 to Visualize “Beam” Modes RBE3’s used to connect various components to centerline. Each component’s centerline grids connected by it’s own set of PLOTELs
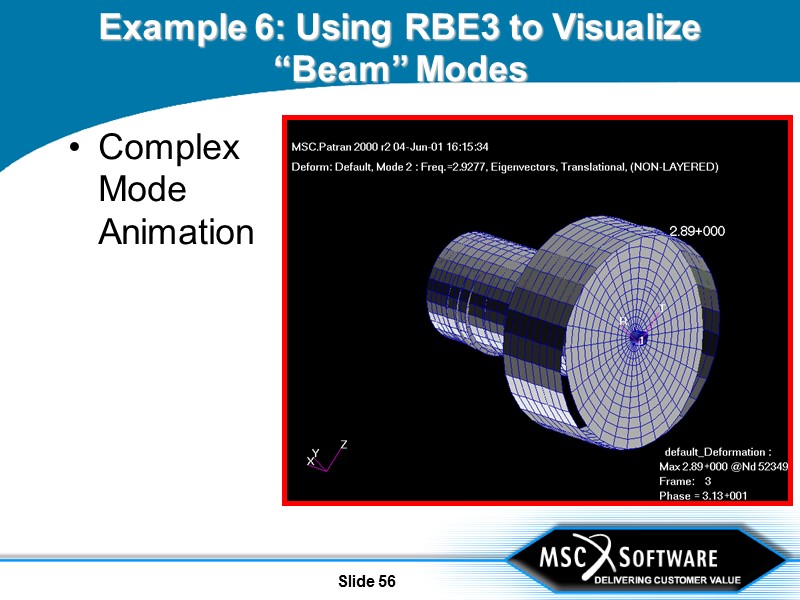
Slide 56 Example 6: Using RBE3 to Visualize “Beam” Modes Complex Mode Animation

Slide 57 Example 6: Using RBE3 to Visualize “Beam” Modes Animation of the PLOTEL segments shows that this is a whirl mode Relative motion of various components more clearly seen

Slide 58 Example 7 Use RBE3 to connect incompatible elements Beam to plate Beam to solid Plate to solid Alternative to RSSCON
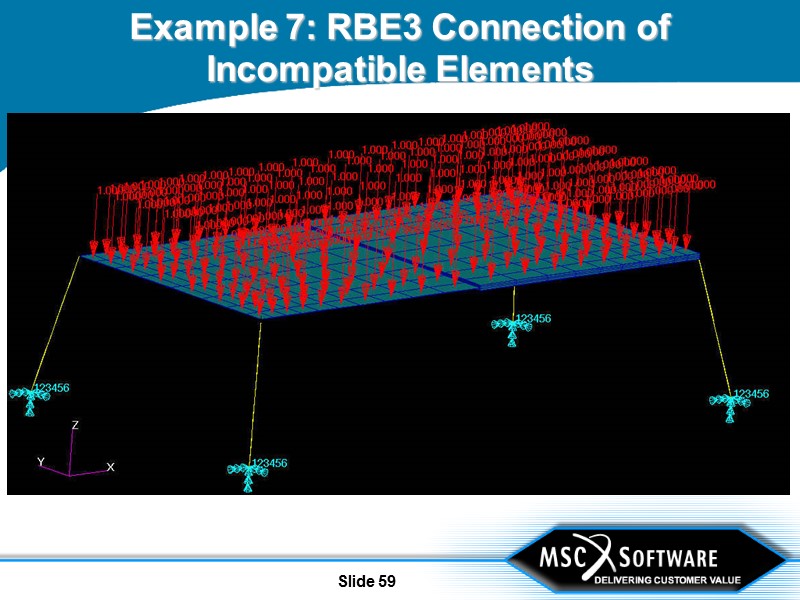
Slide 59 Example 7: RBE3 Connection of Incompatible Elements

Slide 60 Example 7: RBE3 Connection of Incompatible Elements Use RBE3 to connect beams to plates at two corners Use RBE3 to connect beams to solids at two corners Use RBE3 to connect plates to solid Plate thickness is same as solid thickness in this example
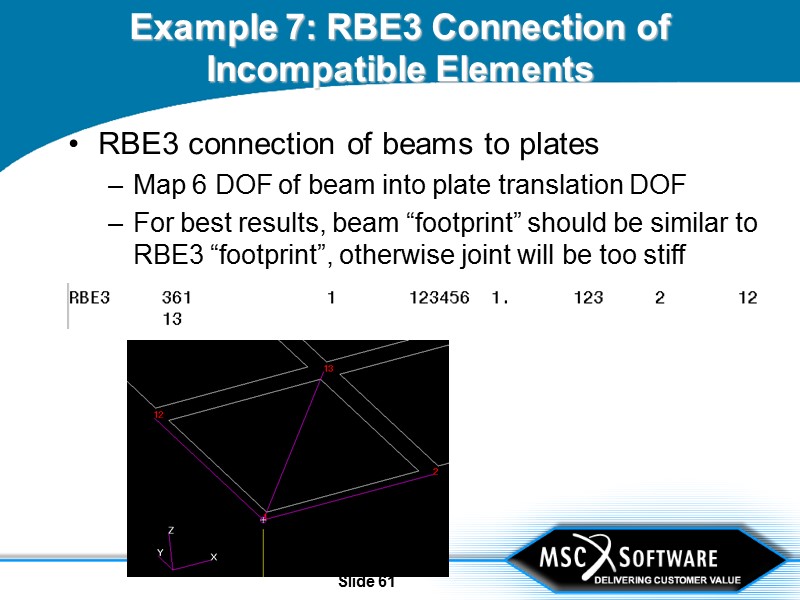
Slide 61 Example 7: RBE3 Connection of Incompatible Elements RBE3 connection of beams to plates Map 6 DOF of beam into plate translation DOF For best results, beam “footprint” should be similar to RBE3 “footprint”, otherwise joint will be too stiff

Slide 62 Example 7: RBE3 Connection of Incompatible Elements RBE3 connection of beams to solids Map 6 DOF of beam into solid translation DOF For best results, beam “footprint” should be similar to RBE3 “footprint”, otherwise joint will be too stiff
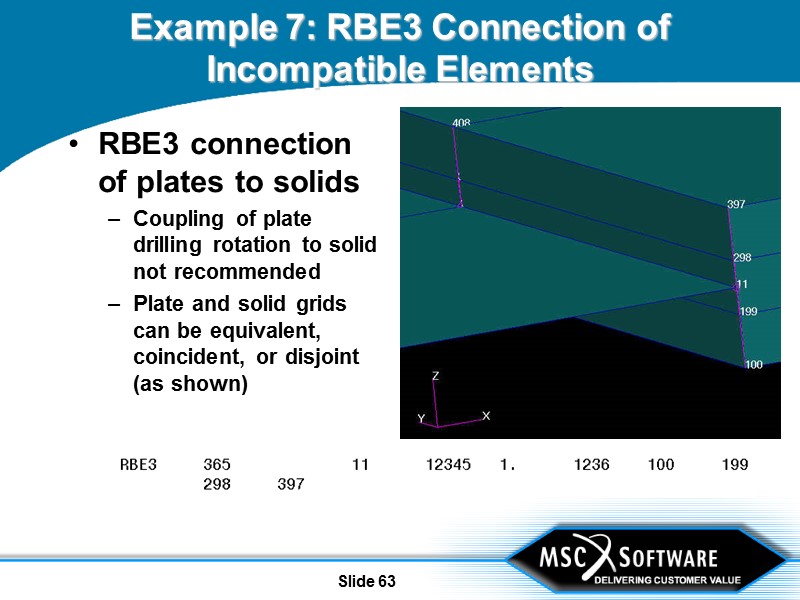
Slide 63 Example 7: RBE3 Connection of Incompatible Elements RBE3 connection of plates to solids Coupling of plate drilling rotation to solid not recommended Plate and solid grids can be equivalent, coincident, or disjoint (as shown)
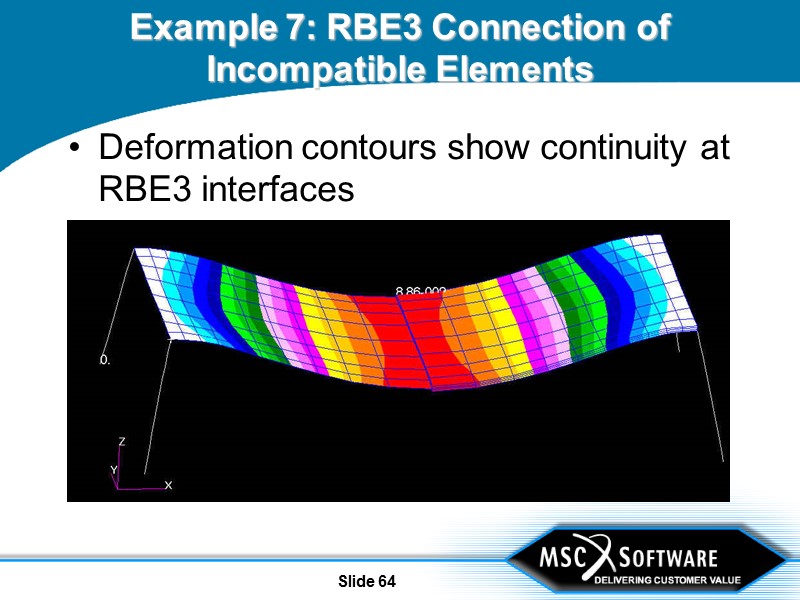
Slide 64 Example 7: RBE3 Connection of Incompatible Elements Deformation contours show continuity at RBE3 interfaces

Slide 65 Example 7: RBE3 Connection of Incompatible Elements Bending stress contours consistent across RBE3 interface

Slide 66 RBE3 Usage Guidelines Do not specify rotational DOF for master grids except when necessary to avoid singularity caused by a linear set of master grids Using rotational DOF on master grids can result in implausible results (see next two slides)

Slide 67 RBE3 Usage Guidelines Example: What can happen if master rotations included? Modified RBE3 from Example 5 Displacements clearly incorrect when all 6 DOF listed for master grids (next page)

Slide 68 RBE3 Usage Guidelines Deformation with all 6 DOF specified for master grids at interface Deformation with 3 translation DOF specified for master grids (same loads/BC’s)

Slide 69 RBE3 Usage Guidelines Make check run with PARAM,CHECKOUT,YES Section 9.4.1 of MSC.Nastran Reference Manual (V68) EMH printout should be numeric zeroes (no grounding) No MAXRATIO error messages from decomposition of Rgmm and Rmmm matrices (numerically stable) Perform grounding check of at least KGG and KNN matrix V2001: Case control command GROUNDCHECK (SET=(G,N))=YES V70.7 and earlier: Use CHECKA alters from SSSALTER library

Slide 70 RBE3: Additional Reading Much RBE3 information has been posted on MSC’s Knowledge Base http://www.mechsolutions.com/support/knowbase/index.html

Slide 71 RBE3: Additional Reading Recommended TANs TAN#: 2402 RBE3 - The Interpolation Element. TAN#: 3280 RBE3 ELEMENT CHANGES IN VERSION 70.5, improved diagnostics TAN#: 4155 RBE3 ELEMENT CHANGES IN VERSION 70.7 TAN#: 4494 Mathematical Specification of the Modern RBE3 Element TAN#: 4497 AN ECONOMICAL METHOD TO EVALUATE RBE3 ELEMENTS IN LARGE-SIZE MODELS

Slide 72 User-Input based “Rigid” Elements MPCs Most general-purpose way to define motion-based relationships Could be used in place of ALL other RBEi Lack of geometry makes this impractical Can be changed between SUBCASEs

Slide 73 MPC Definition “Rigid” elements Definition: The motion of a DOF dependent on the motion of (at least one) other DOF Linear Relationship One (1) dependent DOF “n” independent DOF (n >= 1) ajXi = a1X1 + a2X2 + a3X3+…+ anXn

Slide 74 General Approach For Use of MPCs Write out desired displacement equality relationship on a per DOF level Dependent motion = (your equation goes here) 0 = - Ux2 + Ux1 Re-arrange so left-hand side is zero List dependent term first Ux2 = Ux1

Slide 75 MPC Format For example: Set X motion of GRID 2 = X motion of GRID 1 UX2 = UX1 0 = - UX2 + UX1 = (-1.)UX2 + (+1.)UX1

Slide 76 General Approach to MPCs Write down relationship you want to impose on a per DOF level: ajXi = a1X1 + a2X2 +…+ anXn 0 = -aiXi + a1X1 + a2X2+…+ anXn Move dependent term to 1st term on right hand side:

Slide 77 Why would I want to use an MPC? Tie GRIDs together (RBEi) Determine relative motion between GRIDs Maintain separation between GRIDs Determine average motion between GRIDs Model bell-crank or control system Units conversion

Slide 78 Use of MPC to tie GRIDs together Write down relationship you want to impose on a per DOF level: UX2 = UX1 UY2 = UY2 UZ3 = UZ3 qX2 = qX1 qY2 = qY1 qZ2 = qZ1 1 2

Slide 79 MPC, 535, 2, 1, -1.0, 1, 1, +1.0 MPC, 535, 2, 2, -1.0, 1, 2, +1.0 MPC, 535, 2, 3, -1.0, 1, 3, +1.0 MPC, 535, 2, 4, -1.0, 1, 4, +1.0 MPC, 535, 2, 5, -1.0, 1, 5, +1.0 MPC, 535, 2, 6, -1.0, 1, 6, +1.0 Use of MPC to tie GRIDs together Move dependent term to 1st term on right hand side: 0 = -UX2 + UX1 0 = -UY2 + UY2 0 = -UZ3 + UZ3 0 = -qX2 + qX1 0 = -qY2 + qY1 0 = -qZ2 + qZ1
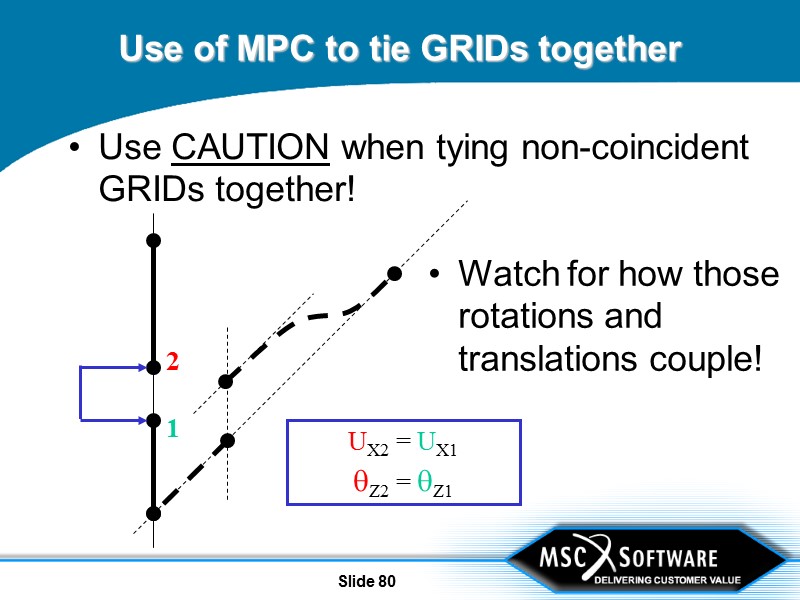
Slide 80 Use of MPC to tie GRIDs together Use CAUTION when tying non-coincident GRIDs together! Watch for how those rotations and translations couple! 2 1 UX2 = UX1 qZ2 = qZ1

Slide 81 MPCs for Relative Motion What’s the relative motion between GRIDs 1 and 2? 1 2 ?
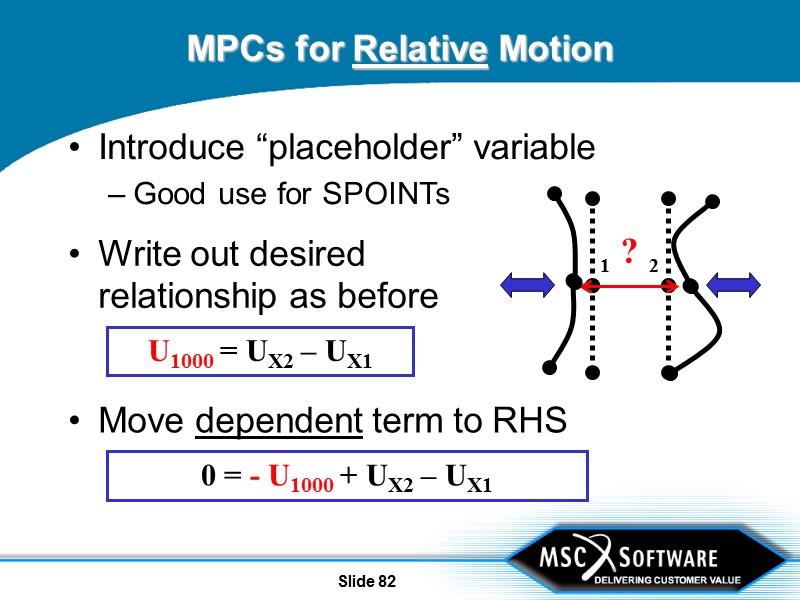
Slide 82 MPCs for Relative Motion Introduce “placeholder” variable Good use for SPOINTs 1 2 ? Move dependent term to RHS 0 = - U1000 + UX2 – UX1 Write out desired relationship as before U1000 = UX2 – UX1
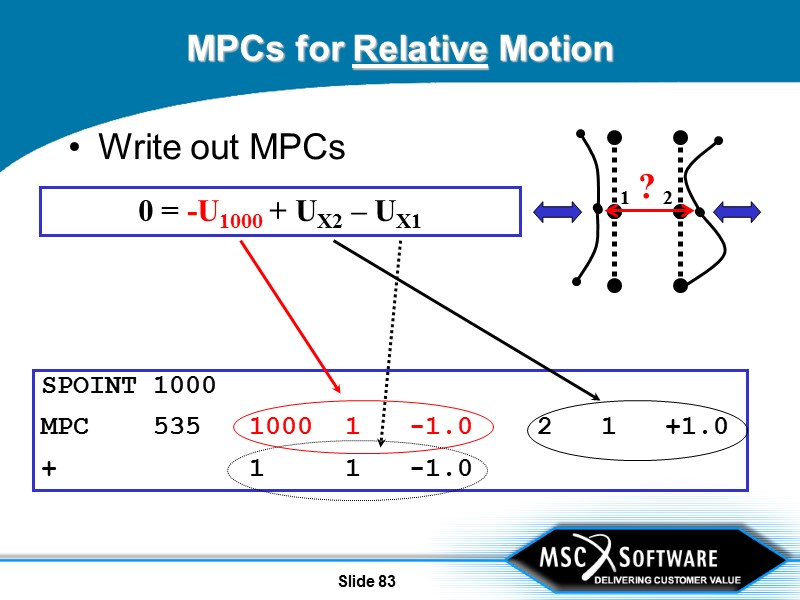
Slide 83 MPCs for Relative Motion Write out MPCs 1 2 ? 0 = -U1000 + UX2 – UX1 SPOINT 1000 MPC 535 1000 1 -1.0 2 1 +1.0 + 1 1 -1.0
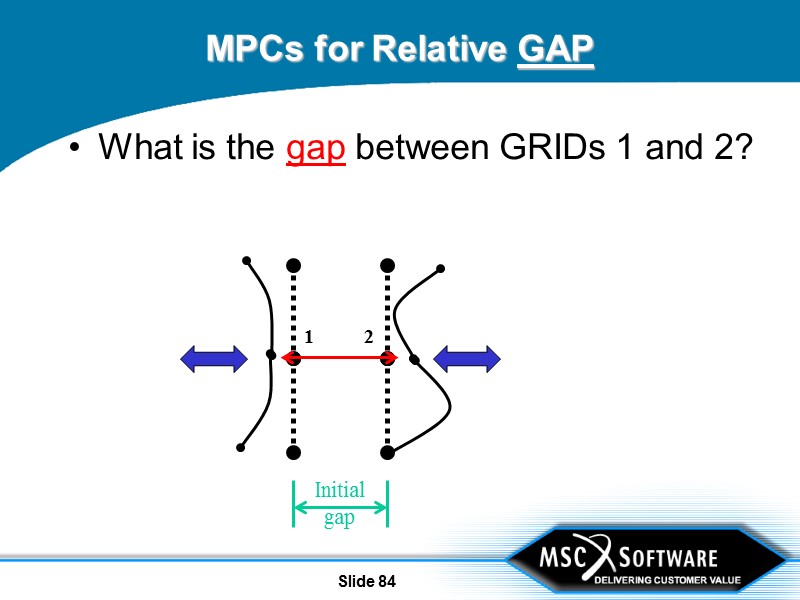
Slide 84 Initial gap MPCs for Relative GAP What is the gap between GRIDs 1 and 2? 1 2

Slide 85 MPCs for Relative GAP 1 2 UGAP = UINIT + UX2 – UX1 0 = -UGAP + UINIT + UX2 – UX1 Write equation: Introduce new placeholder variable for initial gap
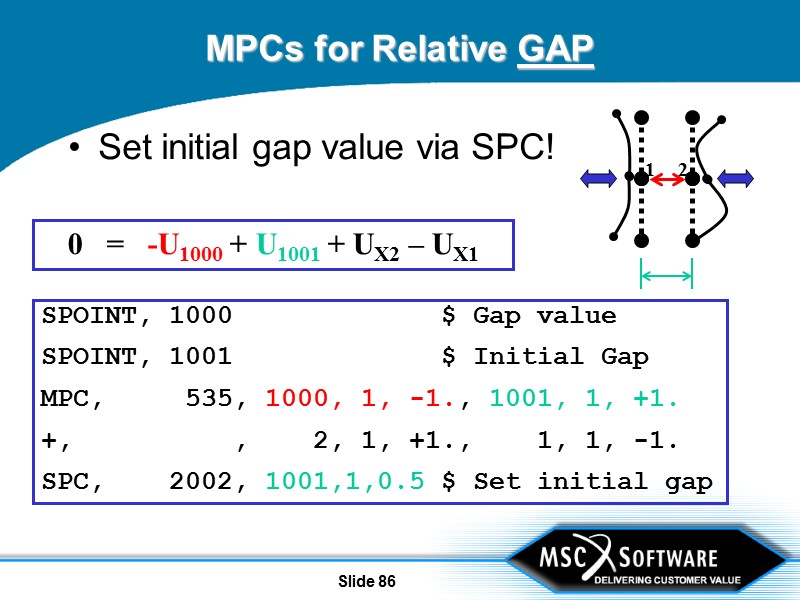
Slide 86 MPCs for Relative GAP Set initial gap value via SPC! 1 2 SPOINT, 1000 $ Gap value SPOINT, 1001 $ Initial Gap MPC, 535, 1000, 1, -1., 1001, 1, +1. +, , 2, 1, +1., 1, 1, -1. SPC, 2002, 1001,1,0.5 $ Set initial gap 0 = -U1000 + U1001 + UX2 – UX1

Slide 87 MPC used to Maintain Separation Enforce a separation between GRIDs Similar to using a gap Changes which DOF are dependent/independent Example: Initially 1” apart Keep separation = 0.25” 1 2 0.25

Slide 88 MPC used to Maintain Separation 1 2 0.25 U1 = U2 + (desired – initial) 0 = -U1 + U2 + U1000 SPOINT,1000 MPC, 535, 1, 2, -1.0, 2, 2, +1.0 +, , 1000, 1, +1.0 SPC, 2002, 1000, 1, -.75 1.00
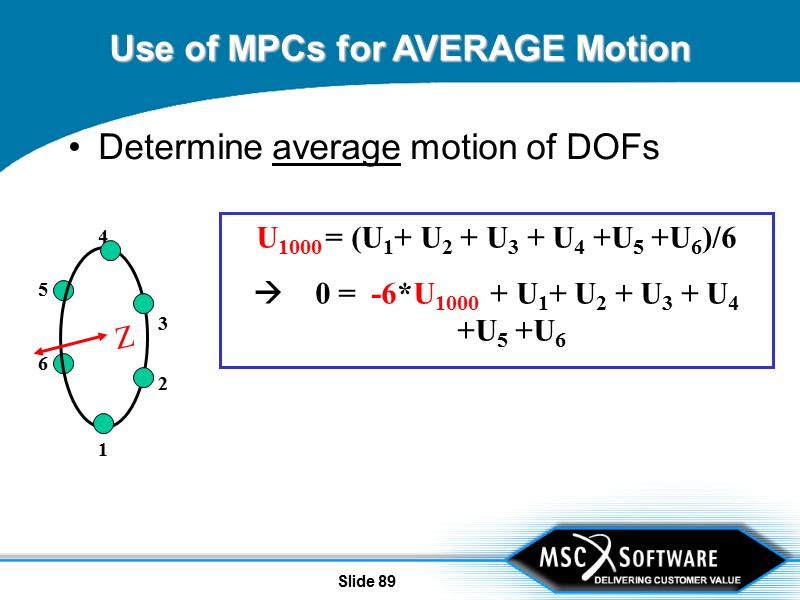
Slide 89 Use of MPCs for AVERAGE Motion Determine average motion of DOFs U1000 = (U1+ U2 + U3 + U4 +U5 +U6)/6 0 = -6*U1000 + U1+ U2 + U3 + U4 +U5 +U6 Z 4 5 2 3 6 1
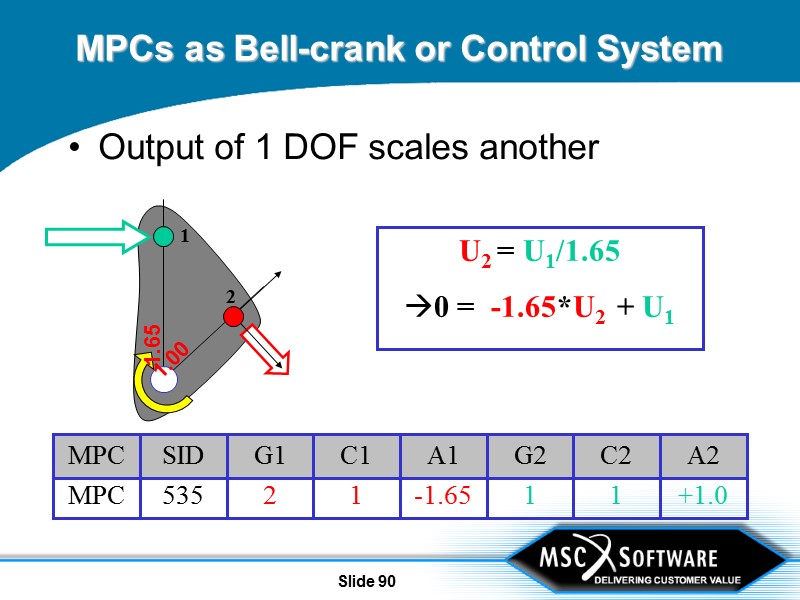
Slide 90 MPCs as Bell-crank or Control System Output of 1 DOF scales another U2 = U1/1.65 0 = -1.65*U2 + U1 2 1 1.65 1.00

Slide 91 Units Conversion Somewhat frivolous application, but why not? Convert radians to degrees q2 = q1 * 57.29578 Convert inches to meters 39.37 * X2 = X1

Slide 92 Rigid Element Output Since Rigid elements are a specialized input of MPC equations, the output is requested by MPCFORCE case control command. COMMON ERROR The MPCFORCEs are associated with GRID IDs, not Element IDs. So when selecting a SET for output, be sure the set is for GRID IDs, not Element IDs.

Slide 93 Guidelines for “Rigid” Elements Linear ONLY Relationships calculated based on initial geometry Can cause internal constraints for thermal conditions Be careful that independent GRID has 6 DOF

Slide 94 MPCs and RBEs Off the shelf RBAR RBE2 Customizable RBE3 Handmade MPC Add them to your modeling arsenal today!
31062-rbe_and_mpc_in_nastran.ppt
- Количество слайдов: 94

