4ea7feccb97f75ac2ba5ea9013605bee.ppt
- Количество слайдов: 47

Развитие математического мышления
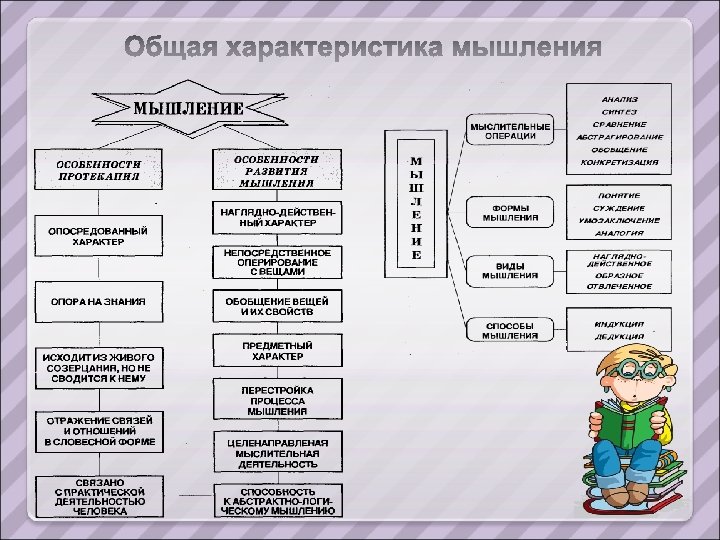

Математическое мышление предельно абстрактное, теоретическое мышление, объекты которого лишены всякой вещественности и могут интерпретироваться самым произвольным образом, лишь бы при этом сохранялись заданные между ними отношения (Л. М. Фридман). Математическое мышление имеет эмпирический и теоретический типы. Подлинное математическое мышление, которое проявляется в самостоятельном решении возникающих задач, является мышлением теоретического типа и имеет аналитический, планирующий и рефлексирующий уровни развития (Р. А. Атаханов): (1) эмпирическое мышление (ЭМ) доаналитический уровень; (2) аналитический уровень теоретического типа мышления (АТМ); (3) планирующий уровень теоретического типа мышления (ПТМ); (4) рефлексирующий уровень теоретического типа мышления (РТМ) собственно теоретическое мышление.

Математическое мышление на своих теоретических уровнях не представляет собой «естественное» продолжение развития эмпирического мышления, а базируется на соответствующих уровнях теоретического мышления. Эмпирический уровень математического мышления проявляется во всех возрастах, может оставаться неизменным во всех возрастных этапах развития школьника, а у значительного числа людей в течение всей жизни. Эмпирическое математическое мышление может иметь разные ступени становления, обусловленные прежде всего ориентированностью на формирование умений и навыков, запоминанием и сохранением в памяти математических фактов. Математическое мышление, ориентированное на нахождение существенного в изучаемых явлениях, также опирается на усвоение и запоминание математических знаний, формирование соответствующих умений и навыков. Они прежде всего используются в качестве исходного материала мысли для выявления существенных отношений в данных объектах, что затем можно применить для решения новых задач. Развитие мышления в этом смысле заключается в непосредственном или опосредствованном переходе от эмпирического мышления к теоретическому как в последовательности уровней мышления вообще, так и в последовательности уровней математического мышления.

Рефлексирующий уровень математического мышления является высоким уровнем и характеризуется полноценным теоретическим типом ориентации в математическом материале. Это выражается в самостоятельном выполнении мыслительных действий содержательного анализа, планирования и рефлексии. Такие учащиеся ориентированы на поиск и выявление исходного отношения уже при решении первых задач и формулирование соответствующих закономерностей, на свернутое выполнение действий в уме и их соотнесение с условиями задачи, на построение системы рассуждений в соответствии со способом решения задачи, а также на осуществление самоконтроля и оценки.

Теоретическое мышление на рефлексирующем уровне развития становится как бы свойством личности и поэтому, при условии владения человеком материалом мысли и наличия у него интереса, может быть реализовано на максимально доступном уровне в любом предметном виде мышления. Умение выполнять мыслительные действия применительно к разному материалу характеризует сформированность мышления вообще, а широкий диапазон такой универсали свидетельствует о высокой культуре мышления человека. В современных условиях обучения (наличие этих условий обусловлено традиционными формами обучения, которые имеют исторические корни, оно связано также с особенностями жизни общества, потребностями и реальными возможностями его сегодняшнего дня) математическое мышление формируется в основном на эмпирическом уровне, а на теоретических уровнях - стихийно. Вместе с тем в специально организованных условиях начального обучения, ориентированных на формирование учебной деятельности (В. В. Давыдов, Л. К. Максимов), в формировании математического мышления преобладает теоретический тип.

Методики, целью применения которых является определение сформированности содержательного анализа, можно составить в разных вариантах: (1) предъявление системы однотипных задач, построенных по единому правилу, где испытуемый может решать эти задачи или путем определения принципа решения, или путем проб и ошибок; (2) предъявление одной задачи, для решения которой необходимо сразу выявить существенное отношение, лежащее в основе способа решения; (3) предъявление задания, состоящего из двух задач, решение которых рассчитано на перенос способа решения. Наличие содержательного анализа устанавливается по выявлению и использованию испытуемым существенного отношения. Решение задач методом проб и ошибок или отсутствие возможности решения задач квалифицируется как эмпирический подход. Аналогично, разные подходы реализуются и при составлении заданий на планирование и рефлексию. Выполнение заданий на планирование и на рефлексию подтверждает наличие или отсутствие этих составляющих теоретического мышления.

Таким образом, испытуемый может выполнить задания блока на уровне содержательного анализа или его отсутствия, т. е. эмпирически. Испытуемым-эмпирикам выполнение заданий на планирование и рефлексию не удается, потому что им недоступен содержательный анализ ситуаций в предлагаемых заданиях. Последовательное предъявление испытуемому адекватных его возрасту заданий позволяет установить наличие одного из четырех уровней развития мышления на неучебном и на математическом материале. При этом : если эмпирическое мышление присуще данному человеку с ограниченной возможностью выхода за его рамки, то аналитический, планирующий и рефлексирующий уровни развития теоретического мышления это закономерные этапы перехода от одного уровня развития мышления к другому. Учащиеся с эмпирическим уровнем развития мышления не могут выполнить содержательный анализ предлагаемого математического материала в любом варианте составления задания: у них отсутствует ориентация на поиск закономерности; они не имеют возможности принятия непрямой подсказки в процессе решения задач, что характеризует ограниченность ученика в выходе за рамки актуальных знаний; возможности развития этой группы учащихся ограничены усвоением типовых действий и их приложений.

В ситуации школьного обучения предметом изучения является некоторым образом упорядоченное содержание учебного предмета. В процессе мышления, преобразовывающего данный материал, происходит формирование соответствующих понятий, которые могут быть составным элементом последующих этапов мышления. Последовательное преобразование объекта мысли приводит к установлению закономерностей и образованию системы соответствующих понятий. Оно сказывается также на особенностях выполнения мыслительных действий при работе с данным материалом, что приводит к формированию некоторого умения выполнения мыслительных действий именно на этом материале. Мыслительные действия теперь выступают как средство преобразования данного конкретного материала. Такое преобразование приобретает специфические черты в зависимости от учебного материала как содержательной основы функционирования мышления, и поэтому характер такого материала может служить критерием различия видов мышления. Если учебный материал относится к образовательной области «математика» , то развиваемое на этом материале мышление математическое. Каждый вид мышления, в том числе, математическое мышление, является носителем свойств, имеющихся и в других видах мышления. Поэтому овладение ими имеет огромное значение для формирования свойств «мышления вообще» .
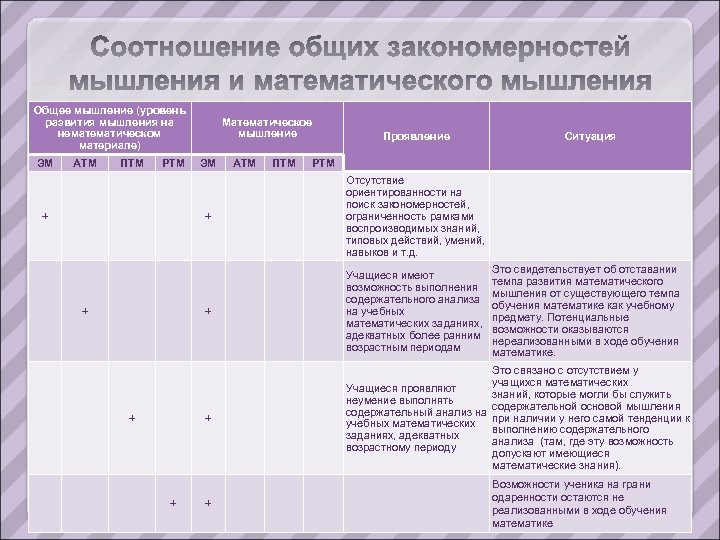
Общее мышление (уровень развития мышления на нематическом материале) ЭМ АТМ ПТМ РТМ Математическое мышление ЭМ АТМ Проявление Ситуация РТМ + + + Учащиеся имеют возможность выполнения содержательного анализа на учебных математических заданиях, адекватных более ранним возрастным периодам + + Отсутствие ориентированности на поиск закономерностей, ограниченность рамками воспроизводимых знаний, типовых действий, умений, навыков и т. д. Это связано с отсутствием у учащихся математических Учащиеся проявляют знаний, которые могли бы служить неумение выполнять содержательной основой мышления содержательный анализ на при наличии у него самой тенденции к учебных математических выполнению содержательного заданиях, адекватных анализа (там, где эту возможность возрастному периоду допускают имеющиеся математические знания). + Это свидетельствует об отставании темпа развития математического мышления от существующего темпа обучения математике как учебному предмету. Потенциальные возможности оказываются нереализованными в ходе обучения математике. Возможности ученика на грани одаренности остаются не реализованными в ходе обучения математике

Общее мышление (уровень развития мышления на нематическом материале) ЭМ АТМ ПТМ РТМ + Математическое мышление ЭМ АТМ ПТМ РТМ + + + + + Уровни развития математического мышления не могут предварять уровни развития общего мышления. Это ограничивает возможности развития математического мышления у учащихся. В зависимости от продолжительности сохранения того или иного уровня мышления его ограниченность можно компенсировать развитием у учащихся других его познавательных возможностей (например, памяти) и личностных особенностей (например, настойчивости), позволяющие обеспечить достижение учащимся значительных успехов в практической деятельности. +

Признаками зарождающегося уровня теоретического мышления обладают учащиеся, которые находятся еще на доаналитической фазе, а также учащиеся с эмпирическим уровнем математического мышления при аналитическом, планирующем или рефлексирующем уровнях мышления вообще. Такая разнородность представителей эмпирического уровня математического мышления требует и соответствующих различий в индивидуальной работе с ними. В актуальном уровне развития мышления вообще выражены потенциальные умственные возможности человека. Эти потенциальные возможности на данном этапе могут быть в определенной мере реализованы человеком. Именно мера реализации учащимися своих умственных возможностей может охарактеризовать успешность организации обучения математике. Сравнение уровня развития мышления вообще и уровня математического мышления у данного ученика и выявленная таким образом дистанция между этими показателями может дать представление о мере реализации его мыслительных возможностей на математическом материале. На фоне обычной системы профессиональной деятельности учителя математики это может привести к изменению им содержания и приемов индивидуального подхода к обучению своих воспитанников.

Внутри установленной последовательности уровней развития мышления вообще и математического мышления (эмпирического, аналитического, планирующего и рефлексирующего) имеются возможности для перевода ученика с одного уровня на другой уровень развития мышления. Одна из возможностей реализации идеи зоны ближайшего развития в способствовании именно такому переходу. При этом сформированность того или иного уровня развития мышления выражается в его рефлексивности, т. е. в умении учитывать все необходимые условия, сопровождающие решение задачи. Развитая рефлексия осуществляется без вмешательства взрослого, самостоятельно.

Понятия являются одной из главных составляющих содержания любого предмета, в том числе и предметов математического цикла. Полноценное изучение математических понятий систематизирует знания учащихся, способствует более глубокому освоению предмета. Первостепенная задача учителя математики пи изучении любой темы – формирование понятийного аппарата темы. Понятие форма мышления, в которой отражены существенные (отличительные) свойства объектов изучения. Понятие считается правильным, если оно верно отражает реально существующие объекты. Каждое понятие может быть рассмотрено по содержанию и объему. Содержание понятия раскрывается с помощью определения, объем - с помощью классификации. Посредством определения и классификации отдельные понятия организуются в систему взаимосвязанных понятий. Содержание понятия это множество всех существенных признаков данного понятия. Объем понятия множество объектов, к которым применимо данное понятие. параллелограмм Например, понятие «треугольник» соединяет в себе класс всевозможных треугольников (объем этого понятия) и характеристическое свойство наличие трех сторон, трех вершин, трех углов (содержание понятия); понятие «уравнение» соединяет в себе класс всевозможных Уравнений (объем понятия) и характеристическое свойство равенство, содержащее одну или несколько переменных (содержание понятия). ромб прямоугольник

Существенные свойства (характеристические) это такие свойства, каждое из которых необходимо, а все вместе достаточны для характеристики объектов, принадлежащих понятию. Мы имеем понятие о некоторой вещи, если знаем и можем словесно выразить, какие условия необходимы и вместе с тем достаточны для ее однозначного определения. Однако, не каждое необходимое условие является достаточным и не каждое достаточное условие является необходимым. Например, равенство двух углов является необходимым условием для того, чтобы эти углы были вертикальные, но не является достаточным. Процесс конструирования понятий заключается в поиске такого числа необходимых условий, которое было бы достаточно для однозначного определения требуемого класса вещей. Совокупность этих условий и принимают за содержание понятия. Содержание понятия раскрывается с помощью определения, объем - с помощью классификации. Так, содержанием понятия «квадрат» является совокупность условий «быть четырехугольником» , параллелограмм «иметь равные стороны» , «иметь равные углы» . Квадрат можно определить как четырехугольник с равными сторонами и равными углами. ромб прямоугольник

Например, для понятия «параллелограмм» содержание будет представлено следующими свойствами: (а) четырёхугольник, противоположные стороны которого равны; (б) четырёхугольник, противоположные стороны которого параллельны; (в) четырёхугольник противоположные углы которого равны; (г) четырехугольник, диагонали которого в точке пересечения делятся пополам и др. Объем понятия «параллелограмм» представлен множествами следующих четырехугольников: (1) собственно параллелограммы; (2) ромбы; (3) прямоугольники; (4) квадраты. По отношению объемов различают следующие виды понятий: Ø равнозначные, объемы которых полностью совпадают; Ø пересекающиеся, объемы которых частично пересекаются; Ø находящиеся в отношении включения, объем одного понятия содержится в объеме другого понятия. ромб прямоугольник параллелограмм

Содержание понятия четко определяет его объем, и наоборот, объем понятия вполне определяет его содержание. Таким образом, изменение в содержании понятия влечет за собой изменение в его объеме, и наоборот. Между содержанием и объемом понятия существует в некотором смысле обратная связь: с увеличением содержания понятия «параллелограмм» (диагонали взаимно перпендикулярны) сразу уменьшается его объем (остаются лишь ромб и квадрат); если уменьшить содержание этого понятия (потребовать параллельности только двух противоположных сторон), увеличится его объем (к названным четырехугольникам добавится трапеция). Если объем одного понятия содержится в объеме другого понятия, то второе понятие называется родовым по отношению к первому понятию, а первое называется видовым по отношению ко второму. Например, понятие «ромб» является родовым по отношению к понятию «квадрат» . Введение понятия через ближайший род и видовые заключается в следующем: (1) указывается род, в который входит определяемое понятие; (2) указываются видовые отличия и связь между ними. параллелограмм Например, «Ромб - это параллелограмм, две смежные стороны которого равны» . Родовым понятием выступает понятие параллелограмма, из которого определяемое понятие выделяется посредством одного видового отличия (равенство смежных сторон). ромб прямоугольник

Формирование понятий – сложный психологический процесс. Он осуществляется и протекает по следующей схеме: ОЩУЩЕНИЯ ВОСПРИЯТИЕ ПРЕДСТАВЛЕНИЕ ПОНЯТИЕ Процесс формирования понятий состоит из мотивации введения понятия, выделения его существенных свойств, усвоения определения, применения понятия, понимания связи изучаемого понятия с ранее изученными понятиями. Формирование понятия осуществляется в несколько этапов: 1. Мотивация (подчеркивается важность изучения понятия, активизируется целенаправленная деятельность школьников, возбуждается интерес к изучению понятия с помощью привлечения средств нематического содержания, выполнения специальных упражнений, объясняющих необходимость развития математической теории); 2. Выявление существенных свойств понятия (выполнение упражнений, где выделяются существенные свойства изучаемого понятия); параллелограмм 3. Формулировка определения понятия (выполнение действий на распознавание объектов, принадлежащих понятию, конструирование объектов, относящихся к объему понятия). ромб прямоугольник
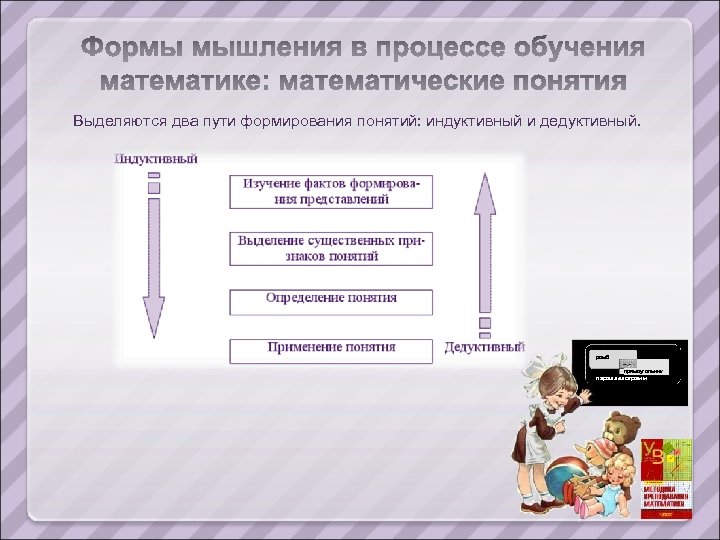
Выделяются два пути формирования понятий: индуктивный и дедуктивный. ромб прямоугольник параллелограмм

Объем понятия раскрывается с помощью классификации. Под классификацией часто понимают последовательное, многоступенчатое разбиение множества на классы с помощью некоторого свойства. Классификация понятий выяснение объема понятий, т. е. разделение множества объектов, составляющих объем родового понятия, на виды. Это разделение основано на сходстве объектов одного вида и отличии их от объектов других видов. Правильная классификация понятий предполагает соблюдение некоторых условий: 1. Классификация должна проводиться по определенному признаку, остающемуся неизменным в процессе классификации. 2. Понятия, получающиеся в результате классификации, должны быть взаимно Натуральные числа независимыми, то есть их пересечение должно быть пустым множеством. 3. Сумма объемов понятий, получающихся при классификации, должна равняться объему исходного понятия. 4. В процессе классификации необходимо переходить к ближайшему в данном родовом понятии виду. 1 Простые числа Составные числа

Заключительным этапом формирования понятия является его определение. Определить понятие это значит перечислить его существенные свойства. Определение понятия это предложение, в котором раскрывается содержание понятия, т. е. совокупность условий, необходимых и достаточных для выделения класса объектов, принадлежащих определяемому понятию. Явные и неявные определения различаются в зависимости от своей структуры. Явные определения содержат прямое указание на существенные признаки определяемого понятия; определяемое и определяющее в них выражено четко и однозначно. Например, «Углом называется фигура, образованная двумя лучами, выходящими из одной точки» ; «Прямоугольник есть параллелограмм с прямым углом» . Явное определение объектов, обозначение выражений, дескрипция ( «Выражение a +. . . + a (n слагаемых) ввиду его важности кратко обозначают n a. Символ n a обозначает сумму n слагаемых, каждое из которых равно a» ). Дескрипциями называются определения математических а +… + а = ап объектов путем указания их свойств ( «То число, которое будучи п слагаемых умножено на длину диаметра, дает длину его окружности» – дескрипция числа π ). Неявные определения объектов не содержат четкого и однозначного определяющего элемента, в них содержание определяемого может быть установлено через некоторый контекст.

Номинальные и реальные определения. Все определения, которые применяются в математике и других науках, делятся на номинальные и реальные, в зависимости от того, что определяется знаковое выражение (термин, символ) или реальный объект, обозначаемый им. С помощью номинального определения вводится новый термин, символ или выражение как сокращения для более сложных выражений из ранее введенных терминов или символов, или уточняется значение уже введенного термина или символа. Номинальные определения являются средством обогащения языка науки и уточнения семантики его выражений ( «Квадратным корнем из неотрицательного числа а называется такое неотрицательное число х , что х2 = а» ). С помощью реальных определений фиксируются характеристические свойства самих определяемых объектов. Деление определений на номинальные и реальные не связано с их формальной структурой. Одно и то же определение можно представить и как номинальное, и как реальное. Например, пусть дано реальное определение: «Пятиугольник – есть плоская геометрическая фигура, ограниченная пятью сторонами» . Это же определение можно переформулировать как номинальное: «Пятиугольником называется плоская геометрическая фигура, ограниченная пятью сторонами» .

Контекстуальные и индуктивные определения. В математике начальных классов часто применяются контекстуальные определения, в которых определение нового неизвестного термина, понятия выясняется из смысла прочитанного, сводится к указанию содержащих его контекстов ( «больше» , «меньше» , «равно» ). Индуктивными называются определения, которые позволяют из сходных объектов (теории) путем применения к ним конкретных операций получать новые объекты. Например, по индукции вводитcя определение натурального числа в математике. Аксиоматические определения. Если определения исходных понятий даются посредством исходных понятий некоторой теории через ее аксиомы, то это аксиоматические определения. При аксиоматическом построении математической теории некоторые понятия остаются неопределенными (например, точка, плоскость и расстояние в аксиоматике А. Н. Колмогорова). Определением этих понятий можно 1 считать систему аксиом, описывающих их свойства. 1+1=2 2+1=3

Определения через род и видовые отличия. Классическими определениями называются определения через род и видовое отличие. Их можно рассматривать как частный вид номинальных определений. В них определяемое выделяется из предметов некоторой области, которая при этом явно упоминается в определении (род), путем указания характеристического свойства определяемого (видовое отличие). В школьном курсе математике определения через род и видовое отличие: Ø Длина ломаной. Ø Периметр многоугольника (прямоугольника, квадрата). Ø Квадрат. Ø Куб. Ø Круг. Ø Радиус окружности (круга). Ø Биссектриса угла. Ø Развернутый угол. Ø Прямой угол. Ø Градус. Ø Острый угол. Ø Тупой угол. Ø Виды треугольников по величине углов. Ø Фигуры, симметричные относительно точки (центр симметрии). Ø Перпендикулярные и параллельные прямые.

Генетические (конструктивные) определения получили широкое распространение в школьном курсе математики. Это такие определения, в которых описывается или указывается способ его происхождения, образования, возникновения, построения. Генетические определения представляют собой разновидность определения через род и видовые отличия. Например: «Сферой называется поверхность, полученная вращением полуокружности вокруг своего диаметра» ; «Шар – это геометрическое тело, образованное вращением полуокружности вокруг диаметра» . Анализируя школьный курс математики, можно выделить следующие генетические определения понятий: Ø Отрезок. Ø Луч. Ø Равносторонний треугольник. Ø Координатный луч. Ø Равные фигуры. С = 2πR Ø Площадь прямоугольника. R Ø Площадь квадрата. Ø Объем прямоугольного параллелепипеда. Ø Окружность. Ø Дуга окружности. Ø Сектор. Ø Угол и его элементы. Ø Равные углы. Ø Длина окружности. Ø Площадь круга.

Определение через абстракцию определения, связанные с выделением абстрактных объектов через установление между ними отношений равенства, равнозначности, тождества. В таком определении данное математическое понятие определяется как семейство классов эквивалентности по некоторому отношению эквивалентности. Например, «натуральное число n это характеристика класса эквивалентных конечных множеств, состоящих из n элементов» . Остенсивные определения значений слов путем непосредственного показа, демонстрации предметов. Часто применяются в начальной школе (понятия отрезка, окружности, угла и др. ). Постепенно с развитием математического опыта и накоплением определенного числа понятий на смену остенсивным понятиям приходят вербальные понятия. Вербальные понятия – это понятия, когда значения неизвестных выражений определяются через выражения, значения которых известны. Определение называется корректным , если выполняются два условия: а) отсутствует порочный круг и связанная с ним возможность исключения нововведенных терминов ( «Решение уравнения это то число, которое является его решением» ); б) отсутствует омонимия: каждый термин встречается не более одного раза в качестве определяемого. окружность

Формой связи понятий друг с другом является суждение. Если суждения правильно отображают объективно существующие зависимости между вещами, то такие суждения называют истинными; в противном случае суждения будут ложными. Процесс получения нового суждения-вывода из одного или нескольких данных суждений называется умозаключением. Важнейшими видами сложных суждений являются теоремы и аксиомы (постулаты). Аксиома (греч. авторитетное предложение «то, что приемлемо» ) предложение, принимаемое без доказательства. Аксиомы и первичные (неопределяемые) понятия составляют основной фундамент математической теории. К системе аксиом, характеризующих некоторую научную теорию, предъявляются требования независимости, непротиворечивости, полноты. Постулат (лат. требование) предложение, в котором выражается некоторое требование (условие), которому должно удовлетворять некоторое понятие или некоторое отношение между понятиями. А, А →С При изучении свойств различных математических объектов приходится делать те или иные заключения, то есть на основе С понятий и суждений того или иного раздела математики строить предложения, истинность которых необходимо обосновать. Математическое предложение, истинность которого устанавливается посредством доказательства (рассуждения), называется теоремой.

Существует два вида формулирования теоремы: условная, категорическая. Всегда можно из одного вида формулирования теоремы перейти в другому. Теорема. В параллелограмме диагонали, пересекаясь, делятся пополам. Если четырёхугольник – параллелограмм, то его диагонали пересекаются и делятся точкой пересечения пополам Условие. Четырёхугольник – параллелограмм Заключение. (1) Диагонали пересекаются. (2) Диагонали делятся точкой пересечения пополам Если теорема сформулирована в условной форме, то в ней должно быть ясно указано: при каких условиях рассматривается в ней тот или иной объект (условие теоремы) и что в этом объекте утверждается (заключение теоремы).

Доказательство теоремы состоит в том, чтобы показать, что если выполняется условие А, то из него логически следует заключение В. Другими словами: приняв, что А истинно, в соответствии с правилами вывода показать, что В истинно, и тем самым получить возможность утвердить, что данное высказывание (теорема) истинно в целом. Доказательство включает в себя три основных элемента: 1. Тезис (главная цель доказательства установить истинность тезиса). Форма выражения тезиса суждение. 2. Аргументы (основания) доказательства положения, на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов суждения. Связывая аргументы, приходим к умозаключению, которые строятся по определенным правилам. Аргументы, на которые можно опереться при доказательстве: аксиомы, определения, ранее доказанные теоремы. 3. Демонстрация логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису.

Известно, что имея некоторую (прямую) теорему А → В), можно образовать новые утверждения: Ø В→А обратное к данной теореме; Ø А → В противоположное к данной теореме; Ø В → А контрапозитивная (обратная противоположной). Между этими четырьмя видами утверждений существует тесная связь: (А → В) и ( В → А) одновременно истинны или ложны; (В → А) и ( А → В) одновременно истинны или ложны.

Изучая какую-либо теорему школьного курса математики, учитель должен придерживаться следующей последовательности: 1. Постановка вопроса (создание проблемной ситуации). 2. Обращение к опыту учащихся. 3. Высказывание предположения. 4. Поиск возможных путей решения. 5. Доказательство найденного факта. 6. Проведение доказательства в максимально простой форме. 7. Установление зависимости доказанной теоремы от ранее известных. Процесс изучения школьниками теоремы включает следующие этапы: 1) мотивация изучения теоремы; 2) ознакомление с фактом, отраженным в теореме; 3) формулировка теоремы и выяснение смысла каждого слова в формулировке теоремы; 4) усвоение содержания теоремы; 5) запоминание формулировки теоремы; 6) ознакомление со способом доказательства; 7) доказательство теоремы; применение теоремы; 8) установление связей теоремы с ранее изученными теоремами.

Рассуждение с целью обоснования истинности какого-либо утверждения есть доказательство. Существуют различные методы доказательства теорем. Под методом доказательства будем понимать способ связи аргументов при переходе от условия к заключению суждения. Методы доказательства, используемые в школьном курсе математики, можно выделить по двум основаниям: по пути обоснования тезиса (прямое и косвенное); по математическому аппарату, используемому в доказательстве. К прямым приемам доказательства относятся: 1. Прием преобразования условия суждения (синтетический). 2. Прием преобразования заключения суждения: а) отыскание достаточных оснований справедливости заключения (восходящий анализ); б) отыскание необходимых признаков справедливости суждения с последующей проверкой обратимости рассуждений (нисходящий анализ). 3. Прием последовательного преобразования то условия, то заключения суждения. К косвенным приемам поиска доказательств относятся: 1. Метод «от противного» (истинность доказываемого тезиса устанавливается посредством опровержения противоречащего ему суждения). 2. Разделительный метод или метод разделения условий (тезис рассматривается как один из возможных вариантов предположений, когда все предположения отвергаются, кроме одного), иначе этот метод называют методом исключения.

К методам доказательства, выделенным по второму основанию, когда способ связи аргументов согласуется с определенной математической теорией в школьном курсе математики, относятся: 1. Метод геометрических преобразований. Э тот метод в школе используется как средство обоснования некоторых отношений между элементами евклидовой геометрии. Состоит он из выполнения последовательности шагов: выбирается геометрическое преобразование, обладающее свойством, которое позволяет обосновать наличие указанного отношения между объектами евклидовой геометрии; выполняется преобразование, при котором один объект переходит в другой; обосновывается наличие указанного отношения между объектами с помощью свойств выбранного геометрического преобразования. 2. Алгебраические методы (уравнений, неравенств, тождественных преобразований). 3. Векторный метод, использующий аппарат векторной алгебры. 4. Координатный метод это способ определения положения точки на прямой, на плоскости или в пространстве с помощью чисел (например, в декартовой системы координат ли какой-либо другой). Используя координатный метод, алгебраические уравнения можно истолковать в виде геометрических образов (графиков или фигур) и, наоборот, искать решение геометрических задач с помощью аналитических выражений (уравнений, неравенств или их систем). При доказательстве математических утверждений используются разные математические методы.

Для того, чтобы учащиеся овладели прямым и косвенным доказательствами, необходимо сформировать у них определенную последовательность умений: - умение искать доказательство, - умение проводить доказательство, - умение оформлять доказательство теоремы. Проведение любого доказательства опирается на три блока знаний и умений: содержательный, структурный, логический. В содержательный блок входят элементы, связанные с ранее изученными математическими понятиями и фактами, которые использованы или в формулировке утверждения, или в качестве аргументов при проведении рассуждений. Эти элементы существенно зависят от логической структуры курса, от его аксиоматики, от методических особенностей изложения и т. д. , а поэтому для одной и той же теоремы в различных учебниках содержательный блок может оказаться различным. В структурный блок входят знания и умения, связанные со структурой утверждения и возможностями ее преобразования. В этот блок входят умения выделять условие и заключение теоремы, преобразовывать логическую форму теоремы с целью получения более простых под теорем и т. д. Логический блок содержит знания и умения, связанные с правилами логических рассуждений.

Стефан Банах Математик это тот, кто умеет находить аналогии между утверждениями; лучший математик тот, кто замечает аналогии теорий; но можно себе представить и такого, кто между аналогиями видит аналогии. С. Банах Обнаружение сходства или различия между предметами поднимает наше мышление на более высокую степень; сосуществовавшие ранее без взаимосвязи знания приобретают новое качество; рассматриваемый предмет познается при этом глубже, подробнее. На основе сравнения понятий строятся умозаключения гипотетические, справедливость которых затем проверяется. Гипотетическими умозаключениями, в частности, являются умозаключения по аналогии. Строя такие умозаключения, учащийся учится умению делать предположения, умению познавать неизвестное, овладевает навыками логического исследования предметов и явлений окружающей действительности.

Возникновение логической формы умозаключений по аналогии можно представить следующим образом. В процессе подчинения себе природы, в ходе изменения окружающего мира для удовлетворения своих потребностей и овладения силами природы, человек сравнивал сходные предметы и явления и многократно замечал следующую связь между ними: если два предмета имеют некоторые одинаковые признаки, то очень часто (но не всегда!) оказывалось, что они имели и некоторые другие общие признаки. Таким образом, умозаключения по аналогии являются умозаключениями вероятности; для того чтобы выяснить достоверность или ложность «вывода по аналогии» , необходимо дополнительно исследовать этот вывод. Этим и отличается рассматриваемый вид умозаключений от индуктивного и дедуктивного умозаключения: если первые приводят к исчерпывающему результату, аналогия лишь открывает путь исследования и не имеет доказательной силы (полная индукция).

Умозаключение по аналогии, будучи рассматриваемо в единстве с процессом доказательства его истинности, диалектично в своей сущности: здесь в теснейшем переплетении и во взаимосвязи встречаются элементы индукции и дедукции. В умозаключении по аналогии прежде всего используется индукция, ибо переход от первого предмета ко второму (от треугольника к тетраэдру, от окружности к сфере) состоит в установлении между одними частными свойствами (простейший многоугольник, наличие трех внутренних углов, существование их равноделящих - биссектрис и др. ). В то же время умозаключение по аналогии тесно связано с дедукцией, ибо истинность вывода по аналогии устанавливается дедуктивным доказательством: то, что в любой тетраэдр можно вписать сферу и при том единственную, надо доказать согласно обычным правилам дедуктивного доказательства. Вывод, полученный прием аналогии, как бы начинается индукцией и завершается дедукцией.

При пользовании аналогией совершается сложный мыслительный процесс, в котором применяются в единстве и взаимопроникновении приемы анализа и синтеза. Так, в приведенном выше примере умозаключение по аналогии стало возможным лишь благодаря тому, что в результате сравнения треугольника и тетраэдра и анализа их свойств устанавливается наличие у них нескольких сходных свойств, которые послужили толчком к предположению о наличии некоторого нового свойства (сферы, вписанной в тетраэдр). Доказательство сформулированного предположения сводится к синтезу понятий, относящихся к тетраэдру, причем он выполняется в том же порядке, в каком выполнялся синтез соответствующих понятий, относящихся к треугольнику (центр вписанной сферы есть точка пересечения биссектральных плоскостей подобно тому, как центр вписанной окружности есть точка пересечения биссектрис). Вывод по аналогии может иногда и не подтвердиться полностью, или подтвердиться лишь частично. Аналогия, как правило, не является доказательным рассуждением, т. е. рассуждением, которое может служить доказательством. (“Как правило” потому, что имеется исключение, связанное с особым видом аналогии. ) Однако в обучении, как, впрочем, и в науке, аналогия часто полезна тем, что она наводит нас на догадки, т. е. служит эвристическим методом. В обучении же математике не менее важно, чем учить доказывать, это учить догадываться, что именно подлежит доказательству и как найти это доказательство.

преподавание математики должно осуществляться на фоне психологического сопровождения; Ø учет индивидуально-психологических особенностей учащихся (возрастные особенности, особенности мотивации учения и т. д. ); Ø целенаправленное формирование эстетического чувства от процесса и результата учебной математической деятельности (развитие эмоциональной сферы учащихся); Ø мобилизация волевых операций учащихся (самоконтроль, самокритика) и оптимизация психических процессов (внимание, воображение, память и пр. ) за счет применения в обучении математике современных компьютерных технологий; Ø использование активных методов обучения; Ø вовлечение учащихся в учебно-исследовательскую и научно-исследовательскую деятельность. Ø Психологическое сопровождение - предполагает отслеживание обучения, развития и воспитания учащихся. Это процесс непосредственного взаимодействия психологической службы и учащихся, их родителей и учителей.


Для построения теории развивающего обучения необходимо в первую очередь описать конкретные условий реализации развивающего обучения по ряду существенных показателей, например: Ø каковы главные психологические новообразования данного возраста, которые возникают, формируются и развиваются в этом возрастном периоде; Ø какова ведущая деятельность данного периода, определяющая возникновение и развитие соответствующих новообразований; Ø каковы содержание и способы осуществления этой деятельности (например, осуществляется она стихийно или целенаправленно); Ø каковы ее взаимосвязи с другими видами деятельности; Ø с помощью какой системы методик можно определять уровни развития соответствующих новообразований; Ø каков характер связи этих уровней с особенностями организации ведущей деятельности и смежных с нею других видов деятельности. Лишь по мере наполнения конкретным содержанием этих показателей (или хотя бы некоторых из них) исследователь или педагог-практик постепенно переходит к оперированию собственно понятием развивающего обучения применительно к вполне определенному возрастному периоду и к тем реальным средствам обучения детей данного возраста, с помощью которых можно осуществлять организацию их ведущей деятельности, приводящую к развитию необходимого уровня соответствующих психологических новообразований

Суть деятельностного подхода состоит в том, что он ориентирует не только на усвоение знаний, но и на способы этого усвоения, на образцы мышления и деятельности, на развитие познавательных сил и творческого потенциала ребенка. Решающим звеном деятельностного подхода является собственная активная учебно-познавательная деятельность учащихся. Структурной единицей учебно-познавательной деятельности является умение доказывать. Ведущая функция этого умения обусловливается тем, что в любом учебном предмете доказательство выступает в качестве метода исследования тех элементов знаний, которые составляют его содержание. Основными целями обучения школьников доказательству в курсе математики являются: Ø обеспечение усвоения учащимися теоретических знаний по курсу математики; Ø формирование у учащихся представления о математике как о дедуктивной науке; Ø обеспечение осознанности, глубины и устойчивости знаний; Ø развитие мыслительной деятельности учащихся.

Исследования, проведенные 3. И. Слепкань, показали, что проблему обучения доказательствам целесообразно расчленить на несколько последовательно решаемых дидактических задач: 1) изучение готовых доказательств, умение воспроизводить их; 2) самостоятельное построение доказательства по образцу с изученным; 3) поиск и изложение доказательств указанным учителем методом или способом; 4) самостоятельный поиск и изложение учащимися доказательств математических утверждений.

Основными направлениями в работе с учащимися по формированию у них умения доказывать могут быть следующие: 1. Показывать учащимся роль и значение доказательства в открытии новых знаний и усвоении учебного материала курса математики. 2. Разъяснять школьникам, в чем состоит сущность доказательства как процесса утверждения или опровержения истинности мыслей. 3. Проводить целенаправленную работу по обучению учащихся пользоваться индуктивным и дедуктивным методами (формировать умение находить общее в отдельных частных примерах, отличать индуктивные умозаключения от дедуктивных, воспитывать у учащихся критическое отношение к индуктивному заключению). 4. Планомерно формировать у учащихся умения выводить логические следствия из посылок, приучать школьников логически верно оформлять свои рассуждения. 5. Формировать у учащихся познавательные действия, необходимые для доказательства, и учить их применять в нужных ситуациях. 6. Учить школьников обобщать познавательные действия, которые выполняются в ходе доказательства.

Как показали исследования ученых (Э. И. Айвазян, М. М. Бурда, 3. И. Слепкань, А. А. Столяр и др. ), умения учащихся доказывать теоремы следует рассматривать как определенные умственные действия трех видов: ориентировочные, исполнительные, контрольнокорректировочные. К ориентировочным действиям относятся: — распознавание понятий, входящих в условие теоремы; — владение алгоритмами доказательств вспомогательных утверждений; — система указаний по осуществлению анализа состава доказываемого утверждения; — система указаний по отысканию планов доказательств; — система указаний по применению конкретных методов доказательств; — обучающие алгоритмы построения планов доказательств определенных групп утверждений. К исполнительным действиям относятся: — действия выведения следствий и выбор следствий, достаточных для доказательства; — действия подведения геометрических фигур под понятия. Контрольно-корректировочные действия включают в себя: — контроль и коррекцию состава условия доказываемого утверждения; — контроль и коррекцию логических этапов доказательства; — контроль и коррекцию полученного результата.

1. Формирование у учащихся умения подмечать закономерности 2. Воспитание у учащихся понимания необходимости доказательства 3. Обучение учащихся умению выделять условие и заключение в математических утверждениях 4. Ознакомление учащихся с простыми и сложными высказываниями и значениями их истинности 5. Ознакомление школьников с понятием отрицания высказываний и с понятием противоречивых высказываний 6. Обучение учащихся умению выделять различные конфигурации на одном и том же чертеже 7. Обучение учащихся умению пользоваться контрпримерами 8. Обучение учащихся умению выполнять геометрические чертежи и читать их 9. Формирование у учащихся умения выводить следствия из заданных условий 10. Формирование у учащихся умения проводить доказательные рассуждения, делать выводы

1. Анализ формулировки теоремы и выяснение ее значения в системе других теорем 2. Построение аналитических рассуждений, облегчающих понимание доказательства теоремы 3. Определение ведущего метода доказательства, исследование особенностей доказательства 4. Исследование математических ситуаций, возникающих при доказательстве 5. Поиск других методов и способов доказательства теоремы 6. Определение рациональной записи доказательства теоремы 7. Подбор задач, решение которых облегчит доказательство теоремы 8. Подбор задач, закрепляющих доказываемую теорему 9. Подбор материала для внеклассной работы, связанного с изученной теоремой
4ea7feccb97f75ac2ba5ea9013605bee.ppt