 Развертки поверхностей
Развертки поверхностей
 Основные положения Развертыванием называется такое преобразование, при котором все точки поверхности совмещаются с плоскостью. Развертка - плоская фигура, получаемая в результате данного преобразования. Поверхности делятся на развертываемые и неразвертываемые. Развертываемые совмещаются с плоскостью без разрывов и складок Для неразвертываемых строятся условные развертки
Основные положения Развертыванием называется такое преобразование, при котором все точки поверхности совмещаются с плоскостью. Развертка - плоская фигура, получаемая в результате данного преобразования. Поверхности делятся на развертываемые и неразвертываемые. Развертываемые совмещаются с плоскостью без разрывов и складок Для неразвертываемых строятся условные развертки
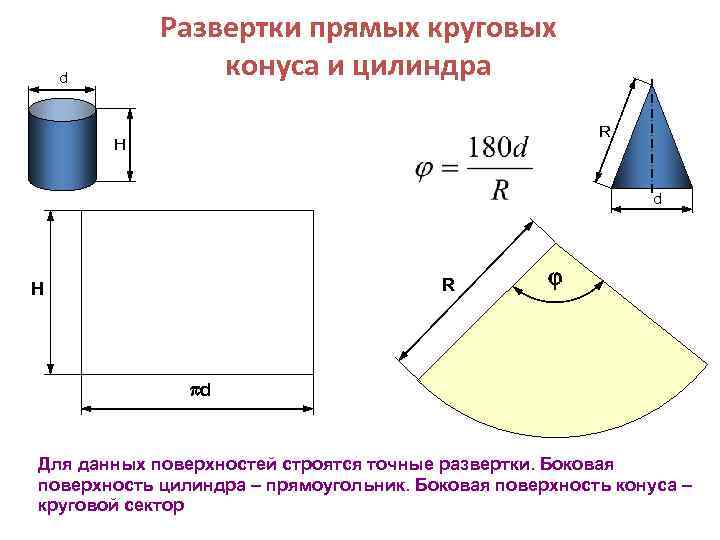 Развертки прямых круговых конуса и цилиндра d R Н d Для данных поверхностей строятся точные развертки. Боковая поверхность цилиндра – прямоугольник. Боковая поверхность конуса – круговой сектор
Развертки прямых круговых конуса и цилиндра d R Н d Для данных поверхностей строятся точные развертки. Боковая поверхность цилиндра – прямоугольник. Боковая поверхность конуса – круговой сектор
 Способ нормального сечения • Определяются натуральные величины образующих, если они заданы в общем положении. • Строится нормальное сечение (там, где образующие имеют истинную величину) • Определяется натуральная величина нормального сечения • Строится развертка: периметр нормального сечение «развертывается» в прямую; через его вершины перпендикулярно линии проводятся образующие Применяется для призматических и цилиндрических поверхностей. Нормальное сечение перпендикулярно образующим и определяет расстояние между ними
Способ нормального сечения • Определяются натуральные величины образующих, если они заданы в общем положении. • Строится нормальное сечение (там, где образующие имеют истинную величину) • Определяется натуральная величина нормального сечения • Строится развертка: периметр нормального сечение «развертывается» в прямую; через его вершины перпендикулярно линии проводятся образующие Применяется для призматических и цилиндрических поверхностей. Нормальное сечение перпендикулярно образующим и определяет расстояние между ними
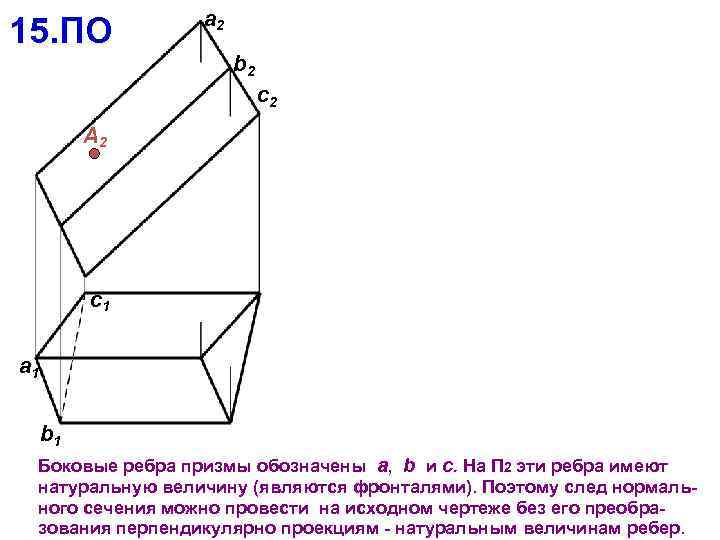 15. ПО a 2 b 2 c 2 А 2 c 1 a 1 b 1 Боковые ребра призмы обозначены a, b и c. На П 2 эти ребра имеют натуральную величину (являются фронталями). Поэтому след нормального сечения можно провести на исходном чертеже без его преобразования перпендикулярно проекциям - натуральным величинам ребер.
15. ПО a 2 b 2 c 2 А 2 c 1 a 1 b 1 Боковые ребра призмы обозначены a, b и c. На П 2 эти ребра имеют натуральную величину (являются фронталями). Поэтому след нормального сечения можно провести на исходном чертеже без его преобразования перпендикулярно проекциям - натуральным величинам ребер.
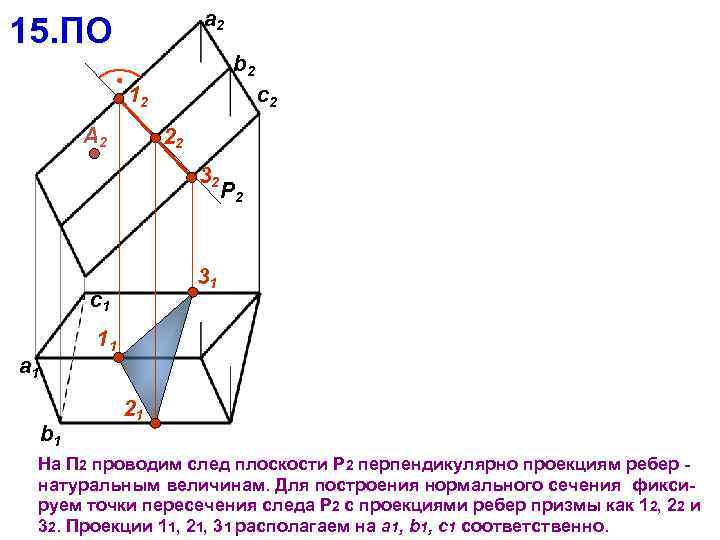 a 2 15. ПО b 2 c 2 12 А 2 22 32 P 2 31 c 1 11 a 1 b 1 21 На П 2 проводим след плоскости Р 2 перпендикулярно проекциям ребер натуральным величинам. Для построения нормального сечения фиксируем точки пересечения следа Р 2 с проекциями ребер призмы как 12, 22 и 32. Проекции 11, 21, 31 располагаем на a 1, b 1, c 1 соответственно.
a 2 15. ПО b 2 c 2 12 А 2 22 32 P 2 31 c 1 11 a 1 b 1 21 На П 2 проводим след плоскости Р 2 перпендикулярно проекциям ребер натуральным величинам. Для построения нормального сечения фиксируем точки пересечения следа Р 2 с проекциями ребер призмы как 12, 22 и 32. Проекции 11, 21, 31 располагаем на a 1, b 1, c 1 соответственно.
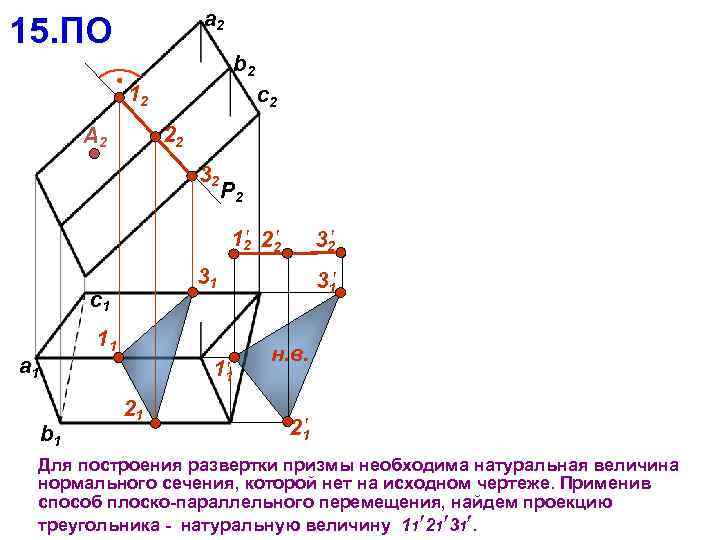 a 2 15. ПО b 2 12 c 2 22 А 2 32 P 2 12 22 31 c 1 11 a 1 11 b 1 32 21 31 н. в. 21 Для построения развертки призмы необходима натуральная величина нормального сечения, которой нет на исходном чертеже. Применив способ плоско-параллельного перемещения, найдем проекцию треугольника - натуральную величину 11 21 31.
a 2 15. ПО b 2 12 c 2 22 А 2 32 P 2 12 22 31 c 1 11 a 1 11 b 1 32 21 31 н. в. 21 Для построения развертки призмы необходима натуральная величина нормального сечения, которой нет на исходном чертеже. Применив способ плоско-параллельного перемещения, найдем проекцию треугольника - натуральную величину 11 21 31.
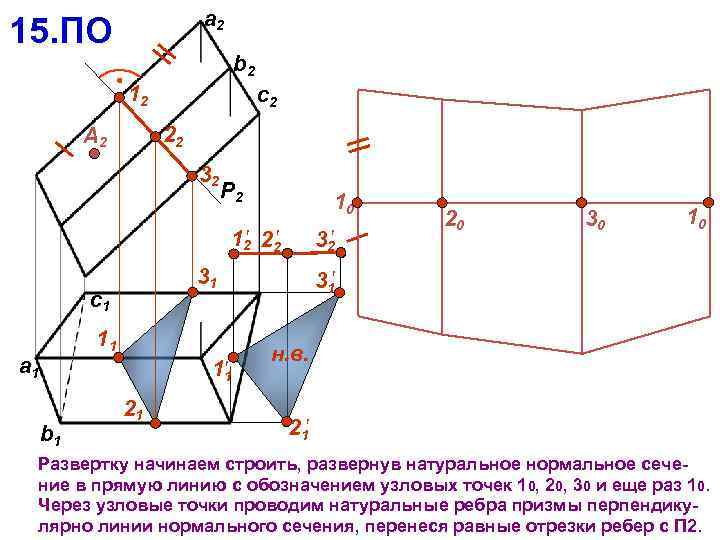 a 2 15. ПО b 2 12 c 2 22 А 2 32 P 2 10 12 22 31 c 1 11 a 1 11 b 1 32 21 20 30 10 31 н. в. 21 Развертку начинаем строить, развернув натуральное нормальное сечение в прямую линию с обозначением узловых точек 10, 20, 30 и еще раз 10. Через узловые точки проводим натуральные ребра призмы перпендикулярно линии нормального сечения, перенеся равные отрезки ребер с П 2.
a 2 15. ПО b 2 12 c 2 22 А 2 32 P 2 10 12 22 31 c 1 11 a 1 11 b 1 32 21 20 30 10 31 н. в. 21 Развертку начинаем строить, развернув натуральное нормальное сечение в прямую линию с обозначением узловых точек 10, 20, 30 и еще раз 10. Через узловые точки проводим натуральные ребра призмы перпендикулярно линии нормального сечения, перенеся равные отрезки ребер с П 2.
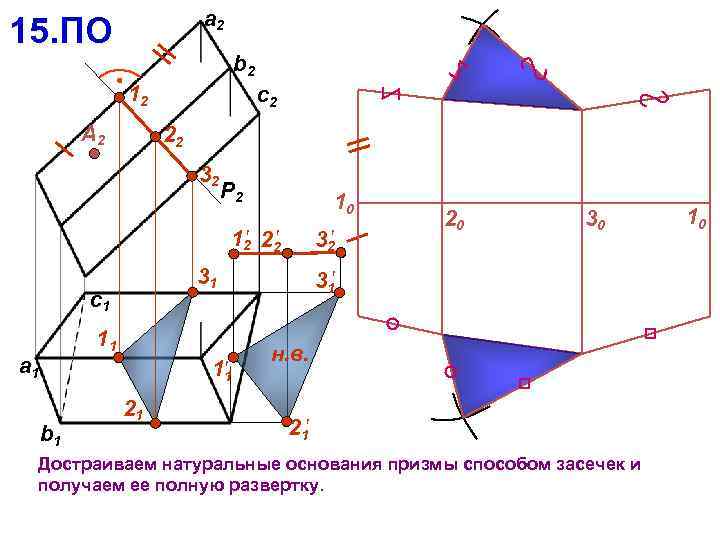 a 2 15. ПО b 2 12 А 2 c 2 22 32 P 2 10 12 22 31 c 1 11 a 1 11 b 1 32 21 20 30 31 н. в. 21 Достраиваем натуральные основания призмы способом засечек и получаем ее полную развертку. 10
a 2 15. ПО b 2 12 А 2 c 2 22 32 P 2 10 12 22 31 c 1 11 a 1 11 b 1 32 21 20 30 31 н. в. 21 Достраиваем натуральные основания призмы способом засечек и получаем ее полную развертку. 10
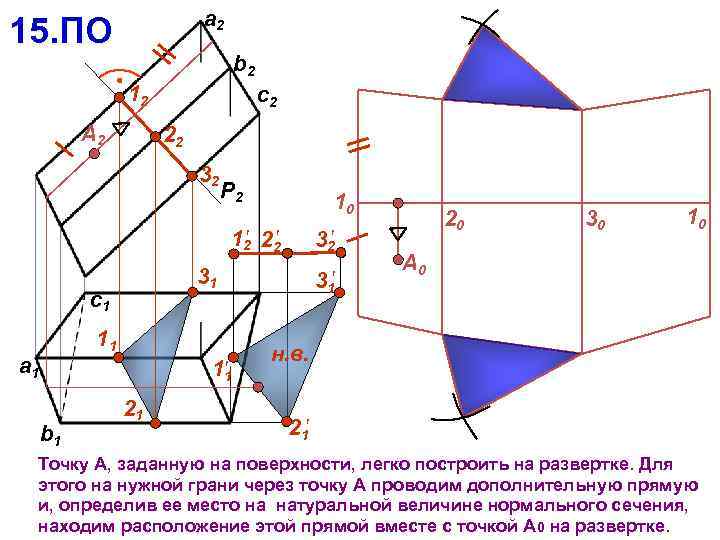 a 2 15. ПО b 2 12 А 2 c 2 22 32 P 2 10 12 22 31 c 1 11 a 1 11 b 1 32 21 3 20 30 10 А 0 1 н. в. 21 Точку А, заданную на поверхности, легко построить на развертке. Для этого на нужной грани через точку А проводим дополнительную прямую и, определив ее место на натуральной величине нормального сечения, находим расположение этой прямой вместе с точкой А 0 на развертке.
a 2 15. ПО b 2 12 А 2 c 2 22 32 P 2 10 12 22 31 c 1 11 a 1 11 b 1 32 21 3 20 30 10 А 0 1 н. в. 21 Точку А, заданную на поверхности, легко построить на развертке. Для этого на нужной грани через точку А проводим дополнительную прямую и, определив ее место на натуральной величине нормального сечения, находим расположение этой прямой вместе с точкой А 0 на развертке.