Разработка алгоритмов и программного обеспечения для обнаружения и параметризации сигналов в экспериментальной физике методами вейвлет-анализа Магистр: Шишкин А. К. Научный руководитель: проф. , к. ф. -м. н. Ососков Г. А.
Существующие проблемы Сложность распознавания сигнала в перекрывающихся гауссах Сложность различения сигналов из-за измерительных шумов Отсутствие программного аппарата для обработки сигналов, полученных в перекрывающихся гауссах.
Цель Создание программы, смоделировать TOF-сигнал и получить его вейвлет спектр.
Задачи Предлагается выполнить две задачи: Написать программу для моделирования сигналов типа изображенных на рис. 1 Написать программу получения вейвлет спектров таких сигналов.
Актуальность темы диссертации определяется потребностями физики высоких энергий (ФВЭ), где одной из важных задач является задача идентификация частиц высоких энергий.
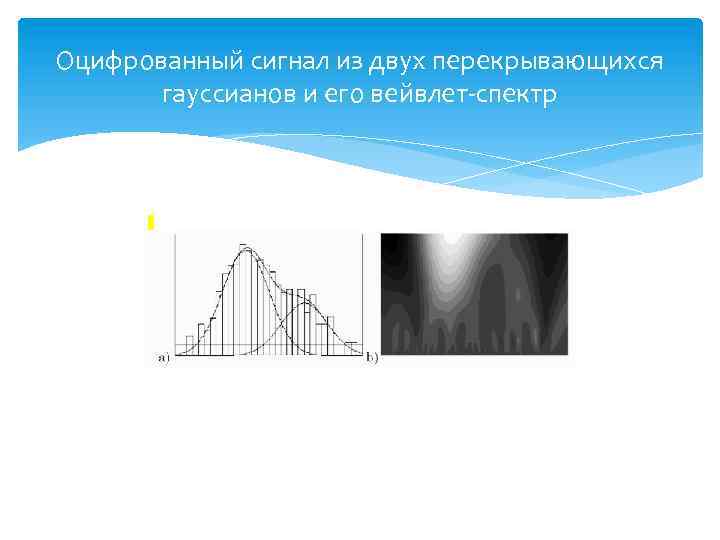
Оцифрованный сигнал из двух перекрывающихся гауссианов и его вейвлет-спектр
Вейвлет-преобразование Вейвлеты (от англ. Wavelet-маленькая волна) — это математические функции, позволяющие анализировать различные частотные и временные компоненты данных. Вейвлеты — это семейство функций, которые локальны во времени, и в которых все функции получаются из одной посредством её сдвигов и растяжений по оси времени. По частоте же вейвлеты меняются посредством сжатиярастяжения и каждый более растянутый по частоте фрагмент, располагается выше в частотном измерении. Эта двухмерность позволяет анализировать сигнал как по месту его возникновения или резких изменений, так и по его частотным обертонам.
Семейство гауссовых вейвлетов Члены любого семейства вейвлетов должны удовлетворять условию-нормирующий коэффициент должен быть конечен ; одно из таких семейств — вейвлеты с нулевыми моментами (Vanishing Momenta Wavelet Family), которые иногда называют гауссовыми вейвлетами.
Время-пролётный детектор время-пролетный детектор TOF нужен для идентификации частиц, полученных в экспериментальных взаимодействиях.
Время-пролётный детектор в составе установки BM@N
Детектор TOF состоит их двух электронных устройств , регистрирующих с высокой точностью время пролета частицы в виде импульсов, имеющих гауссоподобную форму. Первый импульс появляется, когда частица влетает в установку BM@N и он имеет большую амплитуду, второй – при выходе частицы и его амплитуда меньше. Поскольку частицы летят с субсветовыми скоростями, эти импульсы могут перекрываться и тогда выделить обычными методами эти импульсы для определения их центров и вычисления разницы между ними, как времени пролеты, весьма трудно. Особенно в случаях, когда меньший импульс оказывается так близко, что прячется под крылом у большого, так что суммарный сигнал имеет только один максимум. Однако методы вейвлетанализа с непрерывными гауссовыми вейвлетами позволяют получить оценки времени пролета аналитическим путем.
Дальнейшие шаги Проверка написанной программы на смоделированных данных. Внедрение написанной программы в эксперимент BM@N для обработки экспериметальных данных.
Список литературы По данной тематике от руководителя получена следующая литература: 1) Вейвлет-анализ: основы теории и примеры применения( Н. М. Астафьева) 2) Gaussian Wavelet Features and Their Applications for Analysis of Discretized Signals (G. Ososkov , A. Shitov) 3) Разработка методов идентификации частиц во время-проекционной камере детектора MPD на коллайдере NICA С. П. Мерц, С. В. Разин, О. В. Рогачевский. 4) Идентификация заряженных частиц по потерям энергии во время-проекционной камере для эксперимента NICA/MPD (Сергей Мерц) 5)Разработка численных методов и программ, связанных с применением вейвлет-анализа для моделирования и обработки экспериментальных данных(Шитов Андрей Борисович) 6) § 4. Вейвлет-анализ спектров инвариантных масс Абраамян 7)Лекция 7 Введение в вейвлет-анализ с примерами применений в экспериментальной физике Г. А. Ососков
Спасибо за внимание
Скачать презентацию Разработка алгоритмов и программного обеспечения для обнаружения и
Презентация по НИР 2-й семестр Шишкин(last).pptx