Разностные схемы интегрирования дифференциальных уравнений второго порядка схемы

Разностные схемы интегрирования дифференциальных уравнений второго порядка (схемы интегрирования уравнений движения в методе молекулярной динамики) Обозначим тогда уравнение сведется к системе двух уравнений первого порядка I. Схема Эйлера

II. Схема Эйлера – Кромера Схема дает устойчивые решения для колебательных систем III. Метод средней точки Схема имеет 2 -й порядок по х и 1 -й порядок по v. В общем случае он не дает лучших результатов по сравнению с методом Эйлера IV. Метод полушага (метод центральных разностей) Схема высокой точности; несамостартующая; для начала расчетов выбирается

V. Алгоритм Верле Сложив эти разложения, получим Разность разложений: Тогда схема примет вид Полученная схема несамостартующая, так как для начала расчетов необходимо знать два начальных значения. Преимущество в том, что схема имеет третий порядок точности по переменной х и второй по переменной v. Алгоритм Верле наиболее простой и распространенный метод для интегрирования уравнений молекулярной динамики. Если правая часть не зависит от скорости, он позволяет находить координату без вычисления скорости (наиболее эффективен в этом случае)

1. Метод молекулярной динамики в физической химии – М. : Наука, 1996 – 334 с. 2. Кривцов А. М. Деформирование и разрушение твердых тел с микроструктурой – М. : ФИЗМАТЛИТ, 2007. – 304 с. Используются итерационные схемы решения VI. Для начала расчетов Для получения 2 -го порядка точности достаточно 2 итераций (правая часть вычисляется 2 раза). Схема используется как эталонная для проведения методических расчетов

VII. Для начала расчета Далее по схеме. Если ограничиться одной итерацией, то силы вычисляются один раз. Причем вычисляются – скорости вычисляются с меньшей точностью, чем координата, то есть кинетическая энергия вычисляется с меньшей точностью, чем потенциальная. При использовании этой схемы при расчетах хуже сохраняется полная энергия, чем в VI.

VIII. Для реализации схемы нужна только одна итерация (правая часть вычисляется один раз). Скорость и координата вычисляются с одной точностью.

IX. Схема высокой точности (формально ~τ5) Можно сделать одну итерацию (один раз вычислять правую часть), для этого вычисляют

X. Метод Нордзика Более точного расчета позволяет добиться методы типа предиктор – корректор. Наиболее часто используется алгоритм Нордзика, который состоит в следующем: 1. По значениям координат и их производных до степени n включительно определяются аналогичные величины в момент времени t+τ на основе разложения Тейлора. Величина n называется порядком метода (n ≥ 2). 2. Определяются ускорения в момент времени t+τ подстановкой предсказанных значений координат и скоростей в правую часть уравнений. Разность между этими ускорениями и предсказанными называется функцией уточнения и используется для последующей корректировки. 3. Координаты и их производные корректируются добавлением слагаемых, пропорциональных функции уточнения. Коэффициенты пропорциональности различны для каждой производной и подбираются из соображений минимизации ошибки интегрирования. Соответствующие формулы имеют следующий вид. Вводятся переменные, пропорциональные производным радиус вектора частиц

Прогнозируемые значения переменных на следующем шаге вычисляются по формулам Функция уточнения задается формулой где w(t+τ) определяется подстановкой в правую часть уравнения. Окончательно новые значения переменной вычисляются по формулам где ck – корректирующие коэффициенты. Обычно применяются коэффициенты, приведенные в таблице.

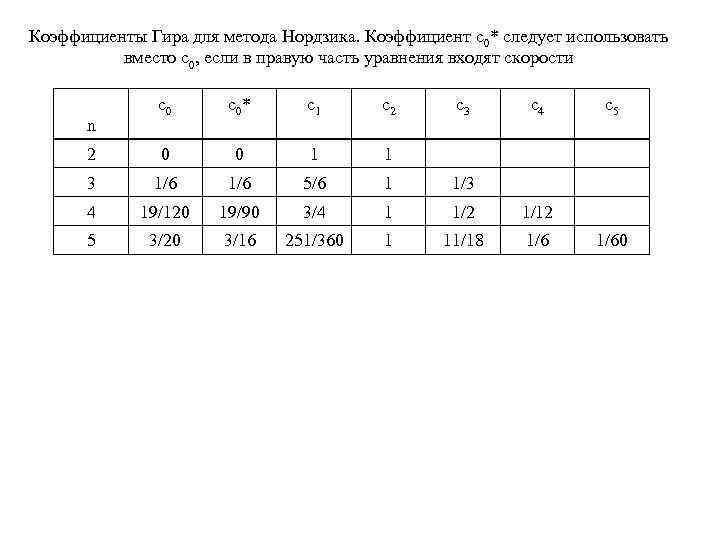Коэффициенты Гира для метода Нордзика. Коэффициент c 0* следует использовать вместо c 0, если в правую часть уравнения входят скорости c 0 * c 1 c 2 2 0 0 1 1 3 1/6 5/6 1 1/3 4 19/120 19/90 3/4 1 1/2 1/12 5 3/20 3/16 251/360 1 11/18 1/6 n c 3 c 4 c 5 1/60

Методы предиктор-корректор позволяют получить значительно более высокую точность при малых шагах интегрирования, чем метод Верле и подобные методы. Однако, для достаточно больших шагов интегрирования метод Верле может оказаться точнее, чем метод Нордзика порядка 3, 4, 5. При этом он требует большего объема вычислений, поэтому выполняется медленнее. Кроме того, недостатком этого метода является необходимость хранения значительного числа данных в памяти – для метода n-го порядка требуется запоминания n+2 векторных величин для каждой частицы, в то время как метод Верле требует хранения всего двух или трех векторных переменных на частицу. Таким образом, этот метод предпочтителен для получения более точных результатов на относительно небольших интервалах времени и при небольшом количестве частиц.