Разностные схемы для уравнений в частных производных

Разностные схемы для уравнений в частных производных • • Классификация уравнений в частных производных Постановка задач для уравнений в частных производных включает определение самого уравнения (или системы нескольких уравнений), а также необходимого количества краевых условий (число и характер задания которых определяется спецификой уравнения). По своему названию уравнения должны содержать частные производные неизвестной функции и (или нескольких функций, если уравнений несколько) по различным аргументам, например пространственной переменной х и времени t. Соответственно, для решения задачи требуется вычислить функцию нескольких переменных, например u

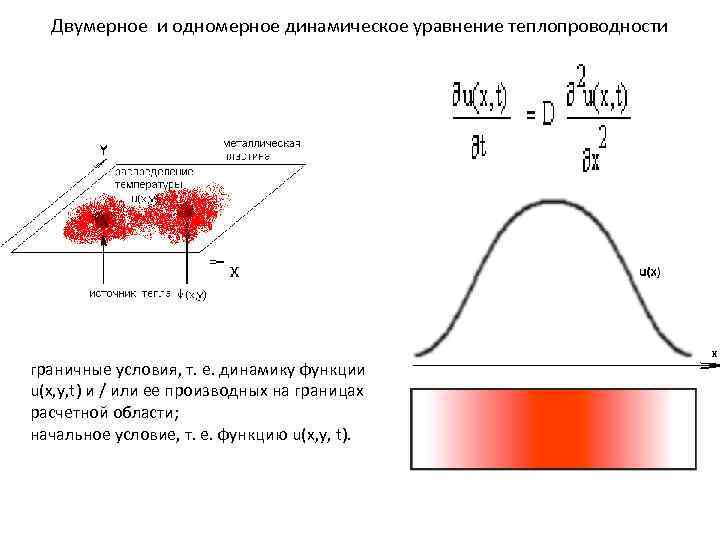Двумерное и одномерное динамическое уравнение теплопроводности граничные условия, т. е. динамику функции u(x, y, t) и / или ее производных на границах расчетной области; начальное условие, т. е. функцию u(x, y, t).

Явная схема Эйлера Шаблон аппроксимации явной схемы для уравнения теплопроводности Линейное уравнение • Решение системы разностных уравнений (9) для модели без источников тепла, т. е. ф(х, T, t)=o и постоянного коэффициента диффузии D=const приведена в листинге 13. 1. В его первых трех строках заданы шаги по временной и пространственной переменным т и Д, а также коэффициент диффузии D, равный единице. В следующих двух строках заданы начальные (нагретый центр области) и граничные (постоянная температура на краях) условия, соответственно. Затем приводится возможное программное решение разностной схемы, причем функция пользователя v(t) задает вектор распределения искомой температуры в каждый момент времени (иными словами, на каждом слое), задава

Явная схема для линейного уравнения теплопроводности

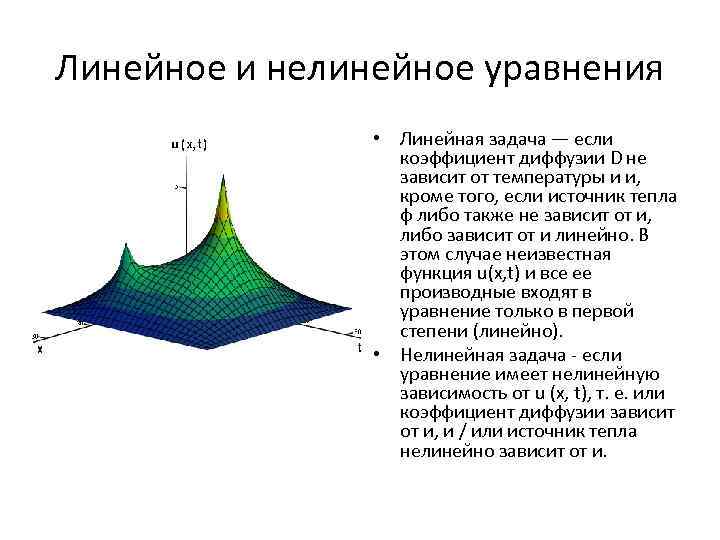Линейное и нелинейное уравнения • Линейная задача — если коэффициент диффузии D не зависит от температуры и и, кроме того, если источник тепла ф либо также не зависит от и, либо зависит от и линейно. В этом случае неизвестная функция u(x, t) и все ее производные входят в уравнение только в первой степени (линейно). • Нелинейная задача - если уравнение имеет нелинейную зависимость от u (x, t), т. е. или коэффициент диффузии зависит от и, и / или источник тепла нелинейно зависит от и.

Нелинейное уравнение • • • Решение уравнения теплопроводности с нелинейным источником и коэффициентом диффузии (режим локализации горения) С физической точки зрения зависимость коэффициента диффузии и функции источника тепла от температуры означает, что эти параметры будут меняться от точки к точке среды, определяясь локальными значениями текущей температуры в этих точках. Ввод ненулевого источника тепла означает, что среда получает определенное количество тепла, тем большее, чем больше локальная температура. Можно догадаться, что введение такой зависимости может моделировать, в частности, горение среды. Если осуществить расчеты с упомянутым источником (имеющим кубическую нелинейность), то получится очень интересное решение уравнения теплопроводности, имеющее профиль тепловых фронтов. С течением времени граница раздела высокой и низкой температуры распространяется в обе стороны от зоны первичного нагрева, оставаясь весьма четко выделенной (рис. 13. 8). Еще более неожиданные решения возможны при нелинейности также и коэффициента диффузии. Например, если взять квадратичный коэффициент диффузии D(x, u)=u 2 (что с учетом его умножения на неизвестные функции создаст кубическую нелинейность уравнения), а также ф(х, u)=10 3 u 3 5, то Вы сможете наблюдать совсем иной режим горения среды. В отличие от рассмотренного эффекта распространения тепловых фронтов, горение оказывается локализованным в области первичного нагрева среды, причем, температура в центре нагрева со временем возрастает до бесконечной величины (рис. 13. 9). Такое решение описывает так называемый режим горения «с обострением» .

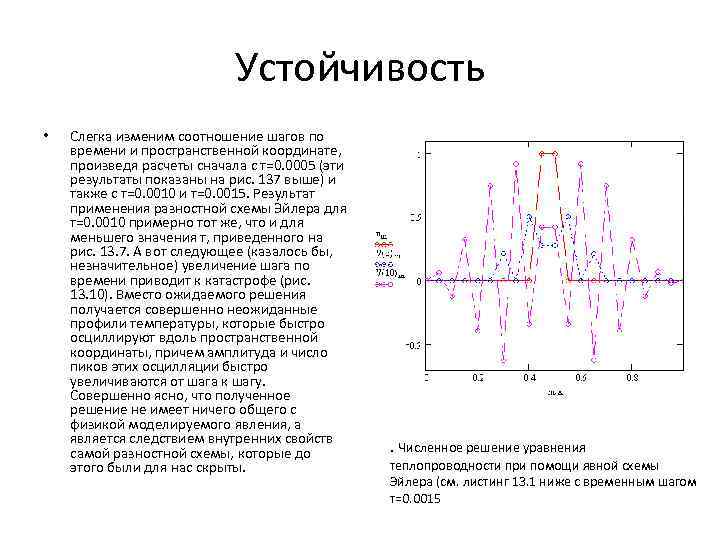Устойчивость • Слегка изменим соотношение шагов по времени и пространственной координате, произведя расчеты сначала с т=0. 0005 (эти результаты показаны на рис. 137 выше) и также с т=0. 0010 и т=0. 0015. Результат применения разностной схемы Эйлера для т=0. 0010 примерно тот же, что и для меньшего значения т, приведенного на рис. 13. 7. А вот следующее (казалось бы, незначительное) увеличение шага по времени приводит к катастрофе (рис. 13. 10). Вместо ожидаемого решения получается совершенно неожиданные профили температуры, которые быстро осциллируют вдоль пространственной координаты, причем амплитуда и число пиков этих осцилляции быстро увеличиваются от шага к шагу. Совершенно ясно, что полученное решение не имеет ничего общего с физикой моделируемого явления, а является следствием внутренних свойств самой разностной схемы, которые до этого были для нас скрыты. . Численное решение уравнения теплопроводности при помощи явной схемы Эйлера (см. листинг 13. 1 ниже с временным шагом т=0. 0015

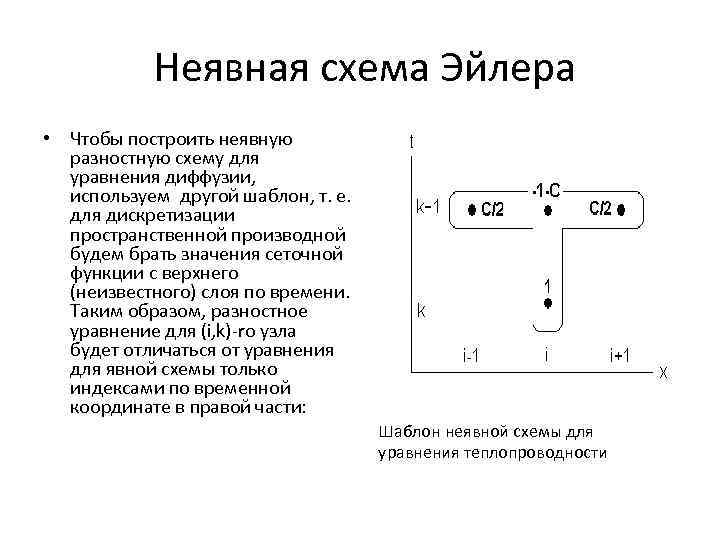Неявная схема Эйлера • Чтобы построить неявную разностную схему для уравнения диффузии, используем другой шаблон, т. е. для дискретизации пространственной производной будем брать значения сеточной функции с верхнего (неизвестного) слоя по времени. Таким образом, разностное уравнение для (i, k)-ro узла будет отличаться от уравнения для явной схемы только индексами по временной координате в правой части: Шаблон неявной схемы для уравнения теплопроводности

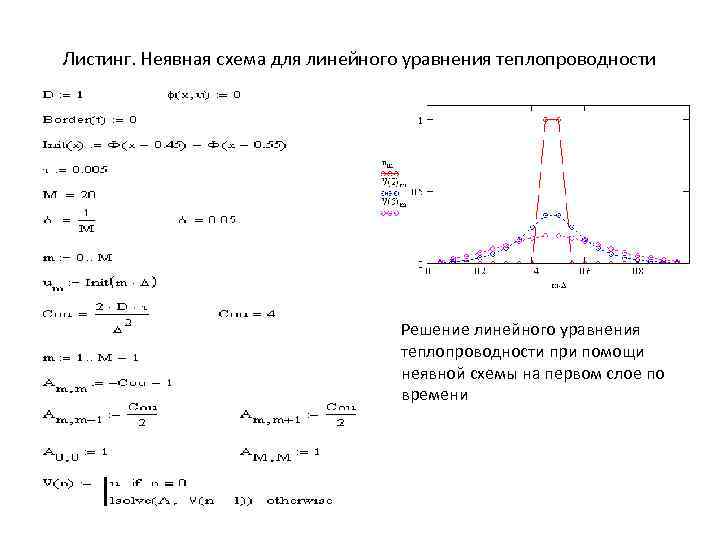Листинг. Неявная схема для линейного уравнения теплопроводности Решение линейного уравнения теплопроводности при помощи неявной схемы на первом слое по времени

Алгоритм прогонки • • Матрица системы линейных разностных уравнений для неявной схемы (листинг для М=10) применение для решения уравнений в частных производных в среде Mathcad может быть оправдано, только если Вы работаете с очень частыми сетками, которые приводят к системам разностных уравнений большой размерности и, соответственно, очень долгому времени вычислений. Основным вычислительным ядром программы, реализующей на Mathcad неявную разностную схему, было решение (на каждом временном слое) системы линейных алгебраических уравнений, задаваемых матрицей А. Заметим, что эта матрица, как говорят, имеет диагональное преобладание, а точнее, является трехдиагоналъной Все ее элементы, кроме элементов на главной диагонали и двух соседних диагоналях, равны нулю. С точки зрения оптимизации быстродействия алгоритма, применение встроенной функции isolve является весьма расточительным, поскольку основной объем арифметических операций, выполняемых компьютером (а он составляет, как нетрудно убедиться величину порядка M 2), сводится к непроизводительному перемножению нулей.

О возможности решения многомерных уравнений • • Алгоритм прогонки (продолжение листинга) Можно ли при помощи Mathcad решать двумерные или трехмерные (пространственные) уравнения? С точки зрения программирования пользователем численных алгоритмов типа метода сеток, принципиальных ограничений нет. Разумеется, если сначала аккуратно выписать разностную схему соответствующего многомерного дифференциального уравнения, то вполне возможно запрограммировать ее при помощи описанных нами средств. Самым главным противодействием будет существенное увеличение времени расчетов. Простая оценка необходимого количества операций показывает, что ввод зависимости уравнения от второй пространственной координаты многократно увеличивает число разностных уравнений, которые должны решаться при реализации каждого шага по времени. К примеру, если используется пространственная сетка из 100 узлов по каждой координате, то вместо 10 2 разностных уравнений на каждом шаге придется решать уже 104 уравнений, т. е. объем вычислений сразу же возрастает в 100 раз. Вообще говоря, пакет Mathcad не является экономичной средой вычислений, и бороться с их сильно возрастающим объемом пользователю следует еще на этапе разработки алгоритма. Хорошим примером такой борьбы может служить применение специфических алгоритмов, типа метода прогонки (см. разд. «Алгоритм прогонки» этой главы).

Встроенные функции для решения уравнений в частных производных Параболические и гиперболические уравнения • Pdesolve(u, x, xrange, t, trange, [xpts] , [tpts])) — возвращает скалярную (для единственного исходного уравнения) или векторную (для системы уравнений) функцию двух аргументов (x, t), являющуюся решением дифференциального уравнения (или системы уравнений) в частных производных. Результирующая функция получается интерполяцией сеточной функции, вычисляемой согласно разностной схеме. – u — явно заданный вектор имен функций (без указания имен аргументов), подлежащих вычислению. Эти функции, а также граничные условия (в форме Дирихле или Неймана) должны быть определены пользователем перед применением функции pdesolve в вычислительном блоке после ключевого слова Given. Если решается не система уравнений в частных производных, а единственное уравнение, то, соответственно, вектор и должен содержать только одно имя функции и вырождается в скаляр. – х —пространственная координата (имя аргумента неизвестной функции). – xrange — пространственный интервал, т. е. вектор значений аргумента х для граничных условий. Этот вектор должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала). – t — время (имя аргумента неизвестной функции). – trange — расчетная временная область: вектор значений аргумента t, который должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала по времени). – xpts — количество пространственных точек дискретизации (может не указываться явно, в таком случае будет подобрано программой автоматически). – tpts — количество временных слоев, т. е. интервалов дискретизации по времени (также может не указываться пользователем явно).

numol (). • Функция numol () имеет еще большее число аргументов и позволяет управлять дополнительными параметрами метода сеток. Однако пользоваться ею намного сложнее, чем функцией Pdesolve (),

Pdesolve(u, x, xrange, t, trange, [xpts] , [tpts])) • Для корректного использования функции Pdesolve предварительно, после ключевого слова Given, следует записать само уравнение и граничные условия при помощи логических операторов (для их ввода в Mathcad существует специальная панель). Обратите внимание, что уравнение должно содержать имя неизвестной функции u(x, t) вместе с именами аргументов (а не так, как она записывается в пределах встроенной функции Pdesolve). Для идентификации частных производных в пределах вычислительного блока следует использовать нижние индексы, например, uxx(, t) для обозначения второй производной функции и по пространственной координате х. .

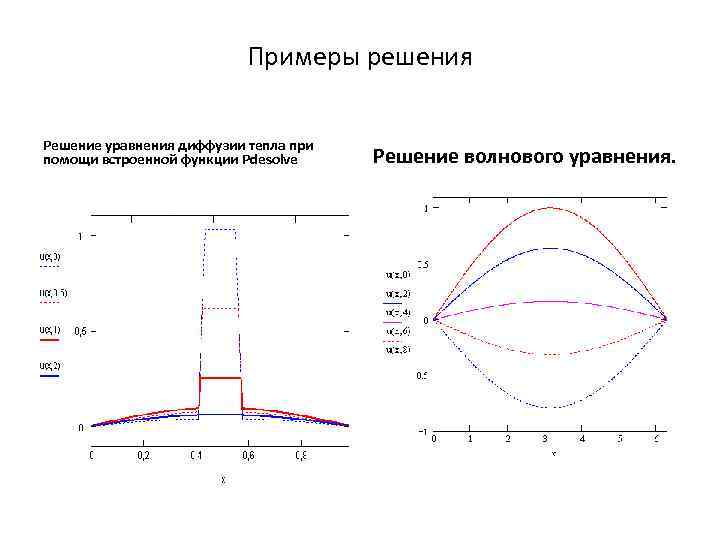Примеры решения Решение уравнения диффузии тепла при помощи встроенной функции Pdesolve Решение волнового уравнения.

Эллиптические уравнения Решение эллиптических уравнений в частных производных реализовано только для единственного типа задач двумерного уравнения Пуассона. Это уравнение содержит вторые производные функции u(х, у) по двум пространственным переменным: Уравнение Пуассона описывает, например, распределение электростатического поля u(х, у) в двумерной области с плотностью заряда f (х, у) или стационарное распределение температуры u(х, у) на плоскости, в которой имеются источники (или поглотители) тепла с интенсивностью f (х, у). Несмотря на то, что применение встроенных функций, описанных в данном разделе, анонсировано разработчиками Mathcad только для уравнения Пуассона, их можно применять и для решения других уравнений, даже необязательно эллиптического типа. О том, как осуществить такие расчеты, написано в конце данного раздела.

Уравнение Пуассона с нулевыми граничными условиями • muitigrid(F, ncycle) — матрица решения уравнения Пуассона размера (M+1)х(M+1) на квадратной области с нулевыми граничными условиями; – F — матрица размера (M+1)X(M+1), задающая правую часть уравнения Пуассона; – ncycie — параметр численного алгоритма (количество циклов в пределах каждой итерации). • Сторона квадрата расчетной области должна включать точно M=2 n шагов, т. е. 2 n+1 узлов, где n — целое число. • Корректная постановка краевой задачи для уравнения Пуассона требует задания граничных условий. В Mathcad решение ищется на плоской квадратной области, состоящей из (м+1)х(м+1) точек. Поэтому граничные условия должны быть определены пользователем для всех четырех сторон упомянутого квадрата. Самый простой вариант — это нулевые граничные условия, т. е. постоянная температура по всему периметру расчетной области. В таком случае можно использовать встроенную функцию multigrid.

Решение уравнения Пуассона с нулевыми граничными условиями. • В первой строке листинга задается значение M=32, в двух следующих строках создается матрица правой части уравнения Пуассона, состоящая из всех нулевых элементов, за исключением одного, задающего расположение источника. В последней строке матрице G присваивается результат действия функции multigrid. Обратите внимание, первый ее аргумент сопровождается знаком "минус", что соответствует записи правой части уравнения Пуассона (11). Графики решения показаны на рис. 13. 16 и 13. 17 в виде трехмерной поверхности и линий уровня, соответственно.

График линий уровня решения уравнения Пуассона

Разностная схема для решения уравнения Пуассона • • • Несмотря на отсутствие сведений в справочной системе Mathcad о решении других линейных дифференциальных уравнений в частных производных, кроме уравнения Пуассона, сделать это возможно с помощью той же функции relax (см. предыдущий разд. ). Для этого нужно правильным образом задать коэффициенты разностной схемы. Начнем с пояснения выбора этих коэффициентов (см. листинг) для уравнения Пуассона. Согласно основным идеям метода сеток (см. разд. «Разностные схемы» этой главы), для дискретизации обеих пространственных производных в уравнении (12) следует использовать по три соседних узла вдоль каждой из координат. Поэтому уравнение Пуассона (12) может быть записано в разностной форме при помощи шаблона типа "крест" (рис. 13. 19). В этом случае после приведения подобных слагаемых в разностных уравнениях коэффициенты разностной схемы будут такими, как показано возле узлов шаблона на этом рисунке (аналогичные коэффициенты для явной и неявных схем решения уравнения теплопроводности см. на рис. 13. 6 и 13. 11, соответственно). Теперь если Вы сравните полученные числа с константами, которые присвоены элементам матриц-аргументов функции relax (см. листинг 13. 7), то увидите, что они как раз и описывают вычисленные нами только что коэффициенты разностной схемы "крест". Таким образом, нетрудно сообразить, что с помощью встроенной функции relax можно решать и другие линейные дифференциальные уравнения в частных производных, которые можно аппроксимировать схемой типа "крест" или схемой, являющейся ее составной частью. Конечно, для того чтобы использовать эту встроенную функцию для другого уравнения, необходимо будет составить соответствующую разностную схему.

Решение уравнения диффузии тепла при помощи функции relax • Результат действия программы листинга 13. 8 показан на рис. 13. 20 в виде трехмерной "поверхности. Если сравнить рис. 13. 20 с рис. 13. 4, полученным при расчетах по запрограммированной разностной схеме, то в графиках рис. 13. 4 нетрудно узнать сечения этой поверхности плоскостями t=const. Еще раз подчеркнем, что использовать встроенную функцию можно только для тех уравнений, которые допускают построение разностной схемы типа «крест» (см. рис. 13. 16) или составного фрагмента этой схемы