Разминка Учитель задал на уроке сложную задачу В

Разминка Учитель задал на уроке сложную задачу. В результате количество мальчиков, решивших эту задачу, оказалось равным количеству девочек, её не решивших. Кого в классе больше: решивших задачу или девочек?

«Мы любим жизнь не из-за самой жизни, а из-за познания»

Методы познания Эмпирические • операциональный ▫ систематическое наблюдение ▫ сравнение ▫ счет ▫ измерение и т. п. • экспериментальный • логико-математический – математическое моделирование векторный метод координатный метод Теоретические • аксиоматический • гипотетико-дедуктивный • описательные методы - словесные, графические, схематические.

"Аксиома - полная недоказуемость, равная полной неопровержимости". Александр Круглов

Аксиома • Аксиома (греч. axíōma — удостоенное, принятое положение, от axióō — считаю достойным), положение некоторой данной теории, которое при дедуктивном построении этой теории не доказывается в ней, а принимается за исходное, отправное, лежащее в основе доказательств других предложений этой теории. Обычно в качестве аксиомы выбирают такие предложения рассматриваемой теории, которые являются заведомо истинными или могут в рамках этой теории считаться истинными.

Аксиоматический метод - способ построения научной теории, при котором в её основу кладутся некоторые исходные положения (суждения) - аксиомы, или постулаты, из которых все остальные утверждения этой науки (теоремы) должны выводиться чисто логическим путём, посредством доказательств.

Суть аксиоматического метода • перечисляются основные (неопределяемые) понятия, • все вновь возникающие понятия должны быть определены через основные понятия и понятия, определенные ранее.

Требования к системе аксиом 1. Непротиворечивость 2. Независимость 3. Полнота

Примеры аксиоматик • В науке • В школе

Аксиомы теории вероятностей

Аксиоматическая теория множеств • Аксиоматическая теория множеств — раздел математической логики, изучающий теорию множеств. • Исходит из развивавшейся Г. Кантором в конце XIX в. «наивной» теории множеств. • Представляет собой построение теории множеств аксиоматическим методом. • Современная теория множеств строится на системе аксиом, из которых выводятся все теоремы и утверждения теории множеств. • Система аксиом Цермело — Френкеля (ZF) является стандартной для теории множеств. К ней часто добавляют аксиому выбора, и называют системой Цермело — Френкеля с аксиомой выбора (ZFC). • Существуют и другие системы аксиом. Например, система NBG (von Neumann — Bernays — Gödel) наряду с множествами рассматривает так называемые классы объектов.

Аксиоматизация геометрии • Проблема полной аксиоматизации элементарной геометрии — одна из проблем геометрии, возникшая в Древней Греции в связи с критикой этой первой попытки построить полную систему аксиом так, чтобы все утверждения евклидовой геометрии следовали из этих аксиом чисто логическим выводом без наглядности чертежей.

Постулаты и аксиомы В «Началах» Евклида утверждения, принимаемые без доказательства, назывались постулатами и аксиомами. Постулаты: 1. Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую линию. 2. И чтобы каждую прямую можно было неопределённо продолжить. 3. И чтобы из любого центра можно было описать окружность любым радиусом. 4. И чтобы все прямые углы были равны между собой. 5. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых. Аксиомы: 1. Равные порознь третьему равны между собой. 2. И если к равным прибавим равные, то получим равные. 3. И если от равных отнимем равные, то получим равные. 4. И если к неравным прибавим равные, то получим неравные. 5. И если удвоим равные, то получим равные. 6. И половины равных равны между собой. 7. И совмещающие равны. 8. И целое больше части. 9. И две прямые не могут заключить пространства.

Аксиоматики • В 1899 году Д. Гильберт предложил первую достаточно строгую аксиоматику евклидовой геометрии.

Аксиоматика Гильберта • Система из 20 аксиом поделена на 5 групп: • аксиомы принадлежности ▫ планиметрические ▫ стереометрические • аксиомы порядка ▫ линейные ▫ Аксиома Паша • аксиомы конгруэнтности ▫ конгруэнтность отрезков ▫ конгруэнтность углов • аксиомы непрерывности Аксиома Архимеда. «Полнота линии» . Добавление хотя бы одной дополнительной точки в прямую линию вызовет противоречие с одной из аксиом принадлежности, порядка, первыми двумя аксиомами конгруэнтности или аксиомой Архимеда. • аксиома параллельности

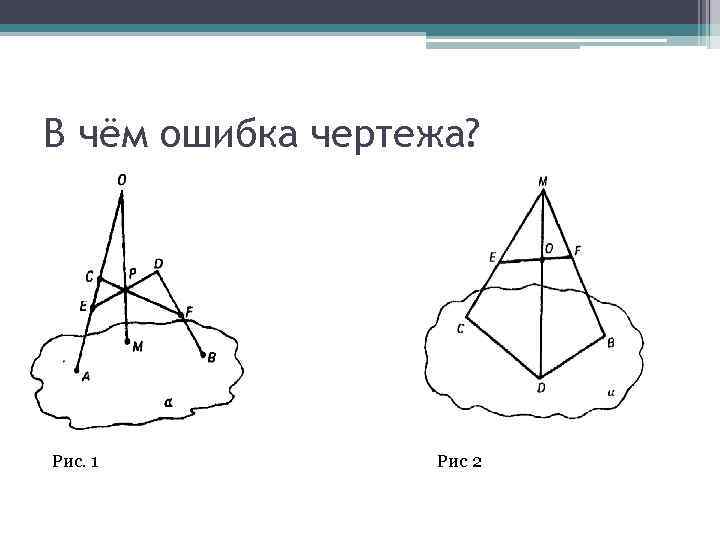В чём ошибка чертежа? Рис. 1 Рис 2

Другие аксиоматики • Кроме Гильбертовой, существуют и другие системы аксиом евклидовой геометрии: родственные – А. В. Погорелова, А. Н. Колмогорова, отличающиеся – А. Д. Александрова, Л. С. Атанасяна и др. • Особо здесь можно отметить систему аксиом Вейля, основанную на понятии вектора, а прямая и плоскость определяются как множества точек.

Непротиворечивость • Непротиворечивость системы аксиом решается представлением ее модели. • А попытки доказательства избыточности системы аксиом геометрии привели к неевклидовым геометриям: Лобачевского, Римана и др.

Неевклидова геометрия Геометрия Лобачевского Геометрия Римана • геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. • В геометрии Лобачевского вместо неё принимается следующая аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. • В геометрии Римана имеют место, например, следующие предложения: через каждые две точки проходит одна прямая, каждые две плоскости пересекаются по одной прямой, каждые две прямые, лежащие в одной плоскости, пересекаются (в одной точке), точки на прямой расположены в циклическом порядке

Домашнее задание 1. В отчёте говорилось, что все 100 участников конференции владеют по крайней мере одним иностранным языком: 5 знают английский, немецкий и французский, 10 – английский и немецкий, 8 – французский и английский, 20 – немецкий и французский, 30 – английский, 23 – немецкий, 50 – французский. Составителям отчёта было указано на ошибки. Почему? 2. На стороне AB треугольника ABC взята точка M такая, что AM: MB=2: 1. Найти длину отрезка CM, если AC=3, BC=4, ACB=1200.