Размещение точек Штейнера в дереве Штейнера на плоскости

Размещение точек Штейнера в дереве Штейнера на плоскости средствами Mat. Lab Поиск трассы на местности 1

Сети коммуникаций l. Несмотря на широкое распространение беспроводных технологий, многие компьютерные сети используют в качестве физической среды передачи информации медные или волоконнооптические кабели. Возникает необходимость прокладывать кабельные сети на земной территории. Земная территория существенно неоднородна. На земле существуют леса, болота, горы, сельскохозяйственные угодья, жилые и хозяйственные постройки. Стремясь минимизировать затраты на прокладку сети следует учитывать, что каждый из элементов такой неоднородности определяет свои условия и стоимость прокладки кабелей. Приходится решать задачу размещения сети в условиях неоднородности. l. Моделью задачи о минимизации этих затрат может быть либо задача о минимальном связывающем дереве (Minimal Spanning Tree – MST), либо задача о минимальном дереве Штейнера - задача Штейнера (Steiner Minimal Tree – SMT). В первой задаче (об MST) разветвления сети допускаются только в соединяемых точках, а во второй задаче (о SMT) разветвления сети допускаются во всех точках области размещения кабелей. Большой интерес и научный и практический представляет задача Штейнера. Известно [1], что на плоскости SMT короче дерева MST на 13. 6%. Но это NP-трудная задача и для ее решения применяются эвристические методы, По задаче Штейнера повсеместно проводятся широкие исследования. Пакет прикладных программ Mat. Lab предоставляет большие возможности в изучении этой задачи. В работе [2], рассмотрена возможность решения трехточечной задачи Штейнера без потока средствами Mat. Lab. В данном докладе представлено продолжение этих исследований. Поиск трассы на местности 2

Трехточечная задача Штейнера l Сеть всяких коммуникаций создается для транспортировки потока, поэтому критерием оптимальности при оптимизации сети должна быть сумма затрат на строительство сети и на транспортировку по ней того потока, для перемещения которого сеть строится. Мы рассматриваем информационный поток, но он может быть также материальным или энергетическим. l Задача минимизации длины дерева – это одна из старейших оптимизационных задач. В середине XVII столетия П. Ферма предложил такую задачу. На плоскости найти точку P, которая минимизирует суммарное расстояние от P до трех заданных точек плоскости. Исследованием этой задачи занимались, Э. Торричелли, Ф. Кавальери и другие математики того времени [3]. Имя «Задача Штейнера» дали этой задаче Р. Курант и Г. Роббинс в книге "Что такое математика" [3]. Якоб Штейнер – геометр, профессор берлинского университета решил эту задачу с помощью циркуля и линейки. Вот это решение. l Если в треугольнике ABC, вершинами которого являются заданные точки A, B, C, все углы меньше 1200 , то точка P лежит внутри треугольника, и каждый из трех углов ے APB ے APC ے BP C равен 1200. Если один из углов треугольника равен или больше 1200, то точка P лежит в вершине этого угла. В книге Р. Куранта и Г. Робинса описан способ решения задачи. Если на каждой стороне треугольника АВС построить дугу в 120 то 0 , то точка пересечения дуг – это искомая точка. на местности Поиск трассы 3

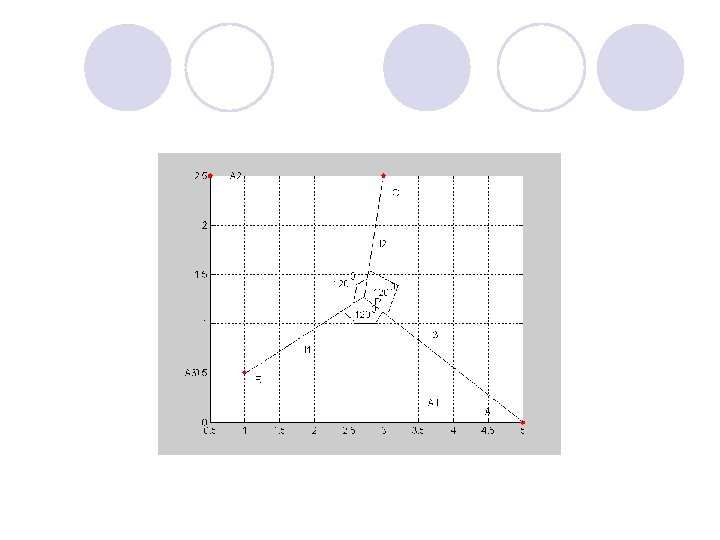
Трехточечная задача Штейнера с потоком на евклидовой плоскости l При размещении сети на земной территории размещается она по условию минимума некоторого критерия. Каждому критерию оптимальности соответствует своя определенная конфигурация сети. В нашей задаче и отдельная коммуникация и сеть коммуникаций проектируются для транспортировки потока, поэтому критерием оптимальности должна быть сумма затрат на строительство сети и на транспортировку по ней того потока, для перемещения которого сеть строится. l Пусть на некотором равнинном участке земной территории задано размещение трех объектов, A 1 , A 2, A 3, из которых объект A 3 является источником некоторого ресурса, а объекты A 1, A 2 – потребителями. В качестве модели этого участка принимается некоторая область на евклидовой плоскости, в которой заданы точки A 1 , A 2, A 3 Эти точки являются образами объектов, размещенных на участке территории. Требуется построить на этом участке сеть транспортных коммуникаций, связывающих источник A 1 , с потребителями, A 2 , A 3, которая обеспечивает протекание потока ресурса при минимальном значении критерия оптимальности. Заданы значения удельных строительных затрат r 1 и значение удельных транспортных затрат r 2. Эти значения определяются свойствами территории, и качеством самой коммуникации. Значение удельных строительных затрат – это затраты на строительство отрезка коммуникации единичной длины. Предполагается, что категория магистралей, определяющая значение удельных строительных затрат r 1 – задана. Поиск трассы на местности 6

Заданная категория магистралей определяет также значение удельных транспортных затрат r 2. Удельные транспортные затраты – это затраты на транспортировку единичного потока по отрезку коммуникации единичной длины, r 2 = const. Спросы потребителей A 1 , A 2 равны q 1 и q 2 соответственно. Учет транспортных затрат меняет в решении задачи локализацию точки Штейнера, длину ребер дерева и величину углов между ними при точке Штейнера. Изменения зависят от значений параметров q 1, q 2, r 1, r 2. Затраты F на строительство сети и на транспортировку по ней потоков величины q 1 и q 2 можно записать в виде, (1) Обозначим f - суммарные – строительные и транспортные – затраты на отрезке коммуникации единичной длины для ребра l 1, l 2, l 3 соответственно, (2) (3) (4) Поиск трассы на местности 7

Поиск точки Штейнера и углов при ней l Теперь выражение (1) можно записать в виде (5) l Это выражение, так же как (1), определяет затраты на строительство сети и на транспортировку по ней потока и является критерием оптимальности. Минимальное значение этого критерия можно достичь, изменяя значения l 1, l 2, l 3. Выполнить это можно, изменяя локализацию точки p. l Критерий оптимальности (5) можно рассматривать как работу сил f 1, f 2, f 3, приложенных к материальной точке p и направленных к точкам A 1 , A 2, A 3, при возможном движении материальной точки p к точкам A 1 , A 2, A 3. Эта работа равна потенциальной энергии материальной точки p относительно точек A 1 , A 2, A 3 [5]. l Известно [5], что потенциальная энергия механической системы имеет строгий минимум в положении устойчивого равновесия системы и что система находится в равновесии, если сумма сил, воздействующих на нее равна нулю. Таким образом, необходимым условием минимума критерия (5) является равенство нулю векторной суммы l (6) =0. Поиск трассы на местности 8

l Углы между векторами в точке p можно определить из соотношения (6). Для этого все векторы , фигурирующие в (6), cпроектируем поочередно на направления, противоположные направлению вектора f 1 , вектора f 2 , вектора f 3. (проекции на направление, противоположное направлению вектора f 3 показаны на рис 1). l l Рис. 1. Проекции сил на направление силы f 3. Раскрывая в (6) суммы пар векторов f 1 f 2, f 1 f 3, f 2 f 3 , получаем три уравнения Поиск трассы на местности 9

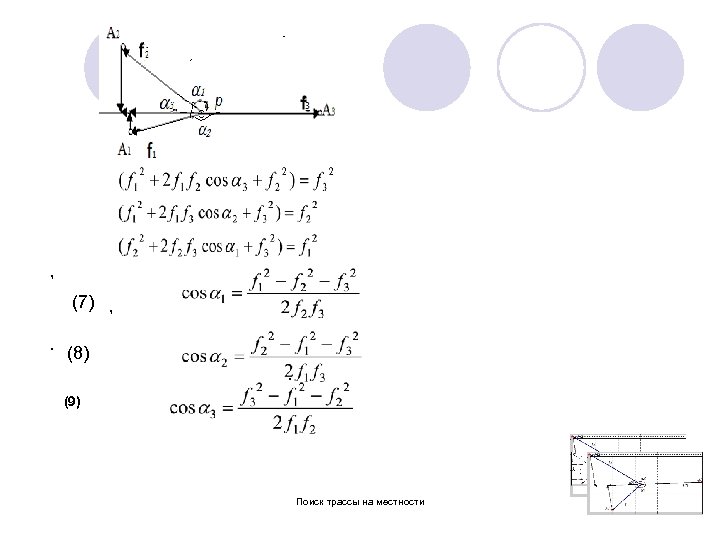, (7) , . (8). (9) Поиск трассы на местности 10

l Если удельные транспортные затраты малы по сравнению с удельными строительными затратами, то ими можно пренебречь, и соотношения l (2) – (4) принимают вид l (9) f 1=f 2=f 3=r 1 l Подставляя эти значения в соотношения (6), (7), (8), получаем, что в дереве Штейнера c нулевым потоком на евклидовой плоскости каждый из углов между ребрами, сходящимися в точке Штейнера равен 1200 , l Этот результат совпадает с результатами, полученными Э. Торричелли, Ф. Кавальери, Я. Штейнером. Если удельными транспортными затратами нельзя пренебречь по сравнению с удельными строительными затратами, то углы становятся отличными от 1200. На следующих слайдах показаны деревья Штейнера на плоскости при различных значениях удельных строительных и удельных транспортных затрат. Показаны поверхности отклика Поиск трассы на местности 11

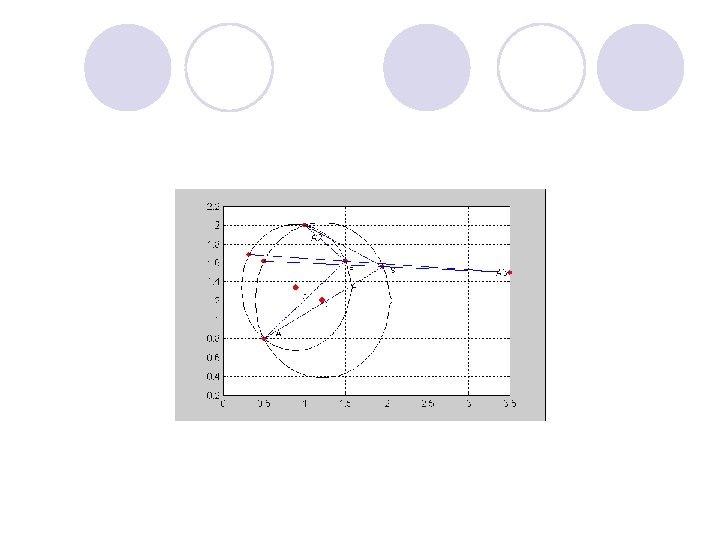
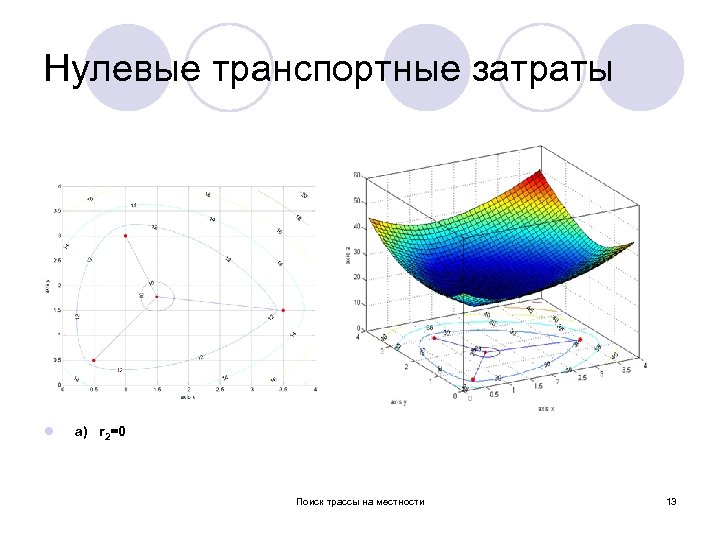Нулевые транспортные затраты l a) r 2=0 Поиск трассы на местности 13

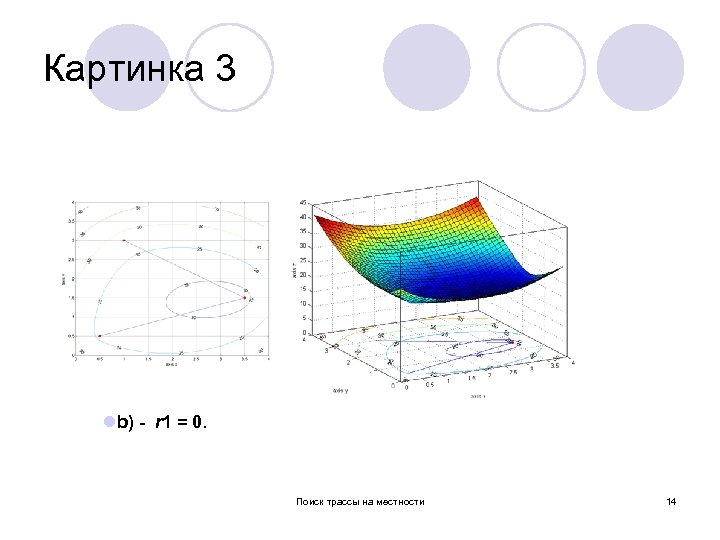Картинка 3 lb) - r 1 = 0. Поиск трассы на местности 14

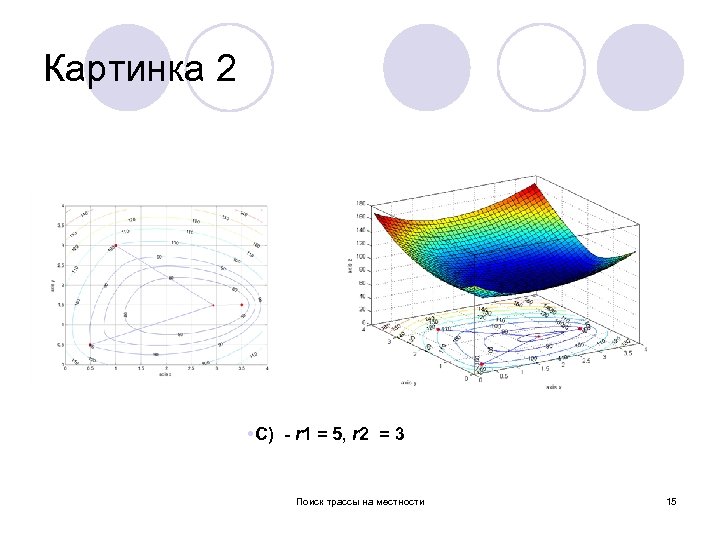Картинкa 2 C) - r 1 = 5, r 2 = 3 Поиск трассы на местности 15

Способ решения l Показанные решения получены средствами пакета ПП Mat. Lab. В этом пакете имеется функция xmin = fminsearch (@Function, x 0), которая ищет минимум функции нескольких переменных - функции (@Function, x 0). Function – это функция, минимум которой ищется, а x 0 - начальная точка поиска. В нашем случае это функция (1), которая определена что на слайде 5. Минимум ищется симплекс-методом Нелдера- Мида. Для плоского случая он состоит в следующем. Для значений функции в трех точках выбирается точка с наибольшим значением функции. Эта точка заменяется точкой, симметричной относительно прямой, проходящей через две другие. Затем операции повторяются. Функция xmin = fminsearch (@Function, x 0) возвращает координаты точки Штейнера и значение минимума. Поиск трассы на местности 16

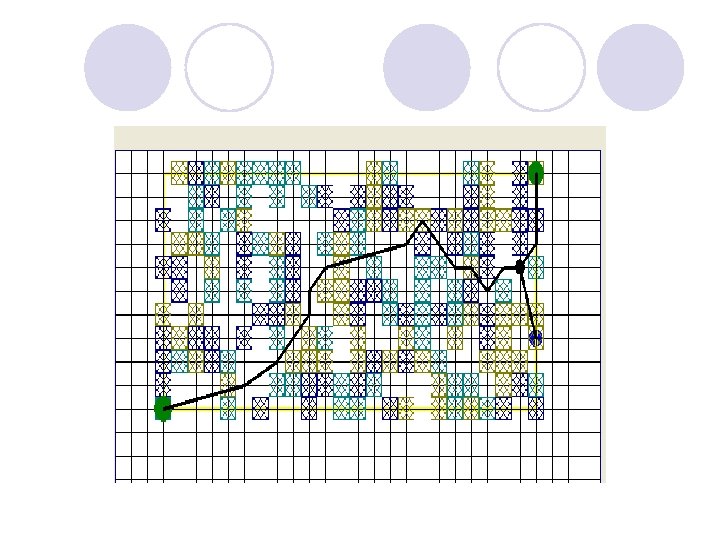
Редукция задачи. Способ 1 l Умение решать трехточечную задачу позволяет редуцировать исходную задачу, в которой число соединяемых точек более 3. l Под редукцией понимается снижение размерности задачи l Первый способ l На первом шаге выполняются следующие операции. l 1. Выбирается корневая вершина будущего дерева – вершина о. l 2. Выбирается самая далекая от корня вершина А и самая близкая к А вершина В. Эти вершины будут концевыми в дереве Штейнера l 3. Для вершин О, А, В решается трехточечная задача Штейнера: разыскивается точка Штейнера S, смежная к вершинам А и В. l 4. Вершины А и В удаляются из первоначального множества, а найденная точка Штейнера добавляется. Тем самым получается задача, аналогичной исходной, но на 1 меньшей размерности. l 5. Операции 2 – 4 повторяются для новых вершин A, B. . Поиск трассы на местности 17

Редукция задачи. Способ 1 l Далее шаги повторяются до тех пор, пока не получится первое приближение всего дерева. l Затем выполняются итерации, на каждой из которых уточняется локализация всех точек Штейнера. l На каждой итерации выполняются следующие операции. l Шаг 1. Выбирается пара концевых вершин А, В, смежная к ним точка Штейнера S 1, и смежная к S 1, точка Штейнера S 2. Для А, В, S 2 решается трехточечная задача, в которой S 2 – корень. В результате получаем уточнение локализации для S 1. . l Шаг 2. Для этой итерации вершины А, В исключаются из дальнейшего рассмотрения, а операции шага 1 повторяются для нового набора вершин А, В, S 1 , S 2. l Когда будет получено уточнение локализации всех точек Штейнера, итерация прекращается. l Число необходимых итераций определяется опытным путем. l На следующем слайде можно увидеть два шага двух итераций.

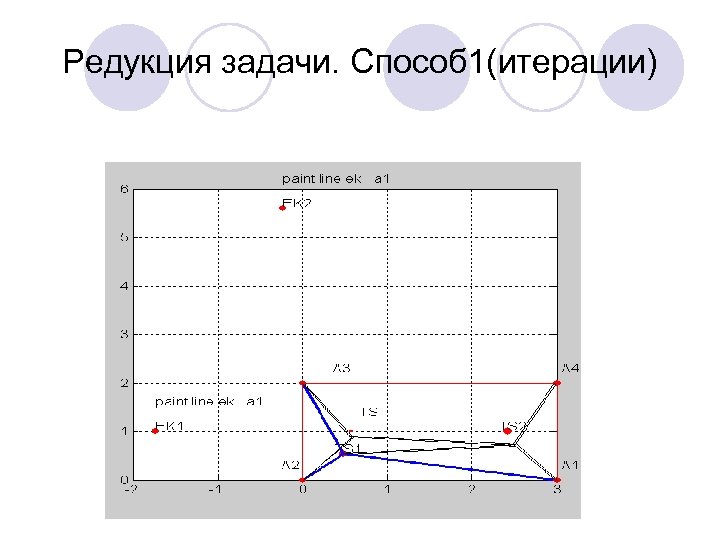Редукция задачи. Способ 1(итерации)

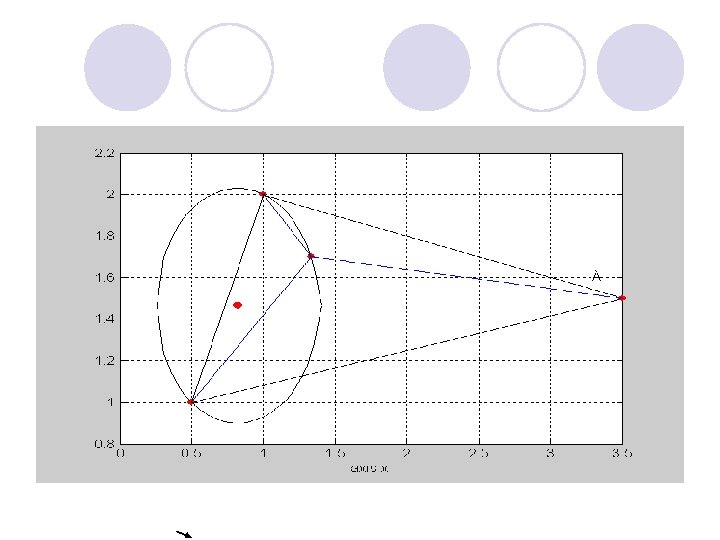
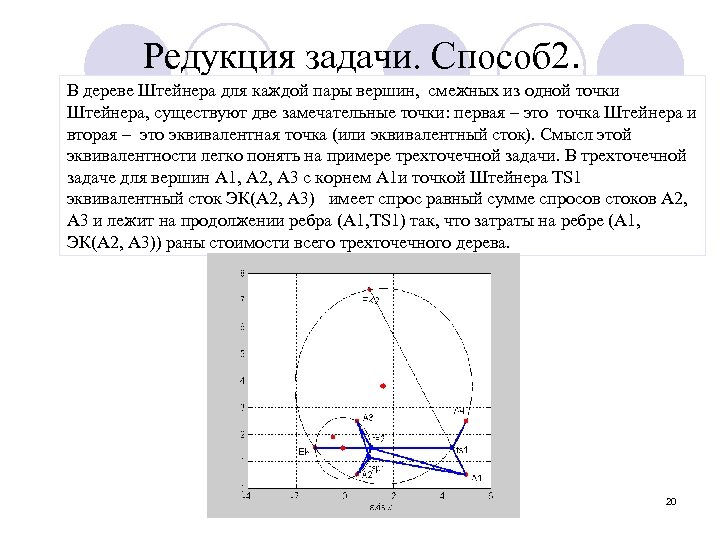Редукция задачи. Способ 2. В дереве Штейнера для каждой пары вершин, смежных из одной точки Штейнера, существуют две замечательные точки: первая – это точка Штейнера и вторая – это эквивалентная точка (или эквивалентный сток). Смысл этой эквивалентности легко понять на примере трехточечной задачи. В трехточечной задаче для вершин A 1, A 2, A 3 с корнем A 1 и точкой Штейнера TS 1 эквивалентный сток ЭК(A 2, A 3) имеет спрос равный сумме спросов стоков A 2, A 3 и лежит на продолжении ребра (A 1, TS 1) так, что затраты на ребре (A 1, ЭК(A 2, A 3)) раны стоимости всего трехточечного дерева. Поиск трассы на местности 20

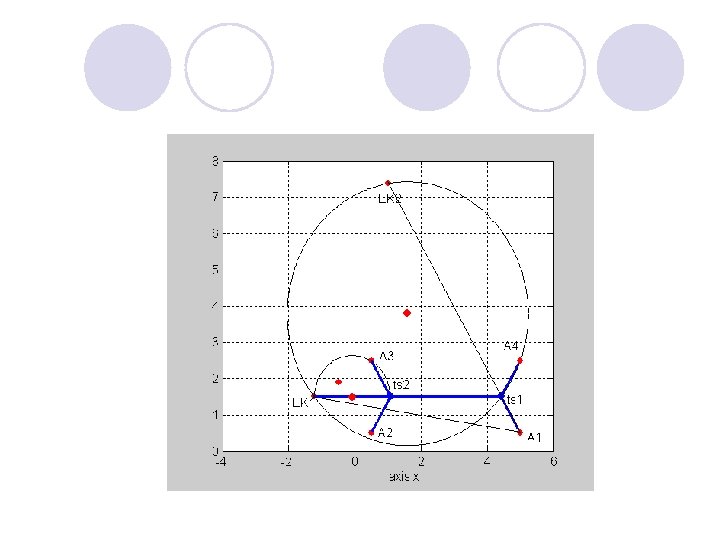
Редукция. Способ 2 l Замена в исходной задаче пары стоков, одним эквивалентным стоком сводит задачу Штейнера для n точек к задаче с n-1 точками. l Вот решение для 5 исходных точек. Найдя локализацию эквивалентного стока ЭК 1, решаем трехточечную задачу для А 1, ЭК 1, А 4 и находим локализацию эквивалентного стока ЭК 2. Решая трехточечную задачу для А 1, ЭК 2, А 5, находим локализацию эквивалентного стока ЭК 3, точки Штейнера TS 3 и ребра (A 1, TS 3), (TS 3, A 5). Теперь решаем трехточечную задачу для (TS 3, EK 1, A 4) и находим точку Штейнера TS 4 и ребра (TS 3, TS 4), (TS 4, A 4). Наконец, решаем трехточе чную задачу для TS 4, A 2, A 3, находим точку Штейнера TS 5 и ребра (Ts 4, TS 5), (TS 5, A 2), (TS 5, A 3). Таким образом мы построили оптимальное дерево Штейнера для пяти исходных точек при заданной матрице смежности. Матрица смежности определяет пары вершин, для которых нужно искать эквивалентный сток. l На слайде 21 показано это дерево. На слайде 22 показано оптимальное дерево Штейнера для шести исходных вершин, построенное по изложенному l алгоритму. Поиск трассы на местности 22

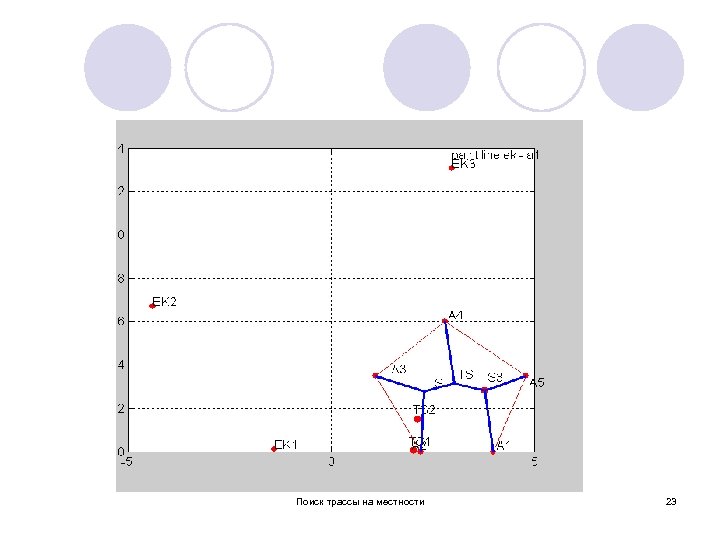Поиск трассы на местности 23

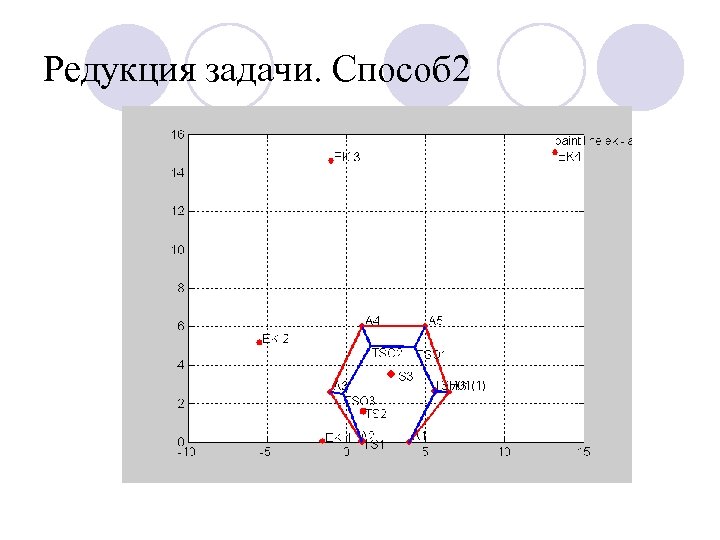Редукция задачи. Способ 2

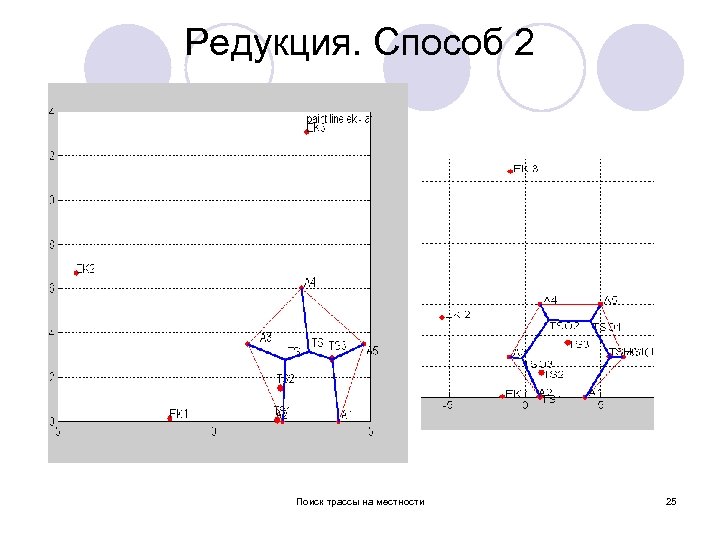Редукция. Способ 2 Поиск трассы на местности 25

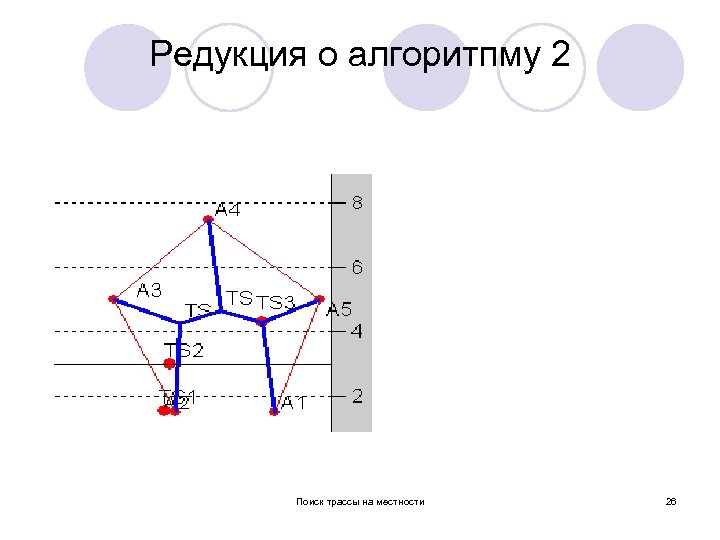Редукция о алгоритпму 2 l Поиск трассы на местности 26