Различные аспекты линейной регрессии LOGO Рассматриваются некоторые

Различные аспекты линейной регрессии LOGO

Рассматриваются некоторые проблемы, часто возникающие при практическом использовании модели линейной регрессии

СПЕЦИФИКАЦИЯ МОДЕЛИ

Основные понятия § Правильная спецификация линейной модели: зависимая переменная, регрессоры и оцениваемые параметры связаны соотношением y b 1 b 2 x 2 …+ bkxk и выполнены все теоретические ограничения § Иначе говоря, соотношение y b 1 b 2 x 2 …+ bkxk является «истинной моделью» На практике § Сам процесс выбора истинная модель неизвестна переменных-регрессоров также называется спецификацией модели

Основные понятия § В процессе выбора возникают две ситуации: § в оцениваемой модели отсутствует часть переменных из истинной модели (исключение существенных переменных) § в оцениваемой модели присутствуют переменные не из истинной модели (включение несущественных переменных) § Процедуры пошагового отбора переменных: § последовательного присоединения, присоединенияудаления и последовательного удаления Реализованы в пакетах программ

Тест на функциональную форму § RESET-тест Рамсея Предварительный этап § добавить в линейную модель новые переменные ─ степени выровненных значений Обычно берутся 2, 3 или 4 степени § вычислить характеристики вспомогательной модели § m ─ количество новых переменных ESSUR – сумма квадратов остатков этой модели ESS – сумма квадратов остатков линейной модели

Правильность спецификации § Тест Рамсея § Основная гипотеза – линейная модель истинная (спецификация правильная) § Альтернативная – линейная модель не истинная (спецификация не верная) Проверка при § Наблюдаемое значение: заданном уровне значимости α § Критическое значение: квантиль уровня 1– α распределения Фишера с m и n – k – m степенями свободы § Выводы: если наблюдаемое больше критического, то спецификация не правильная (с возможной 100α%-й ошибкой) если наблюдаемое меньше критического, то гипотеза о

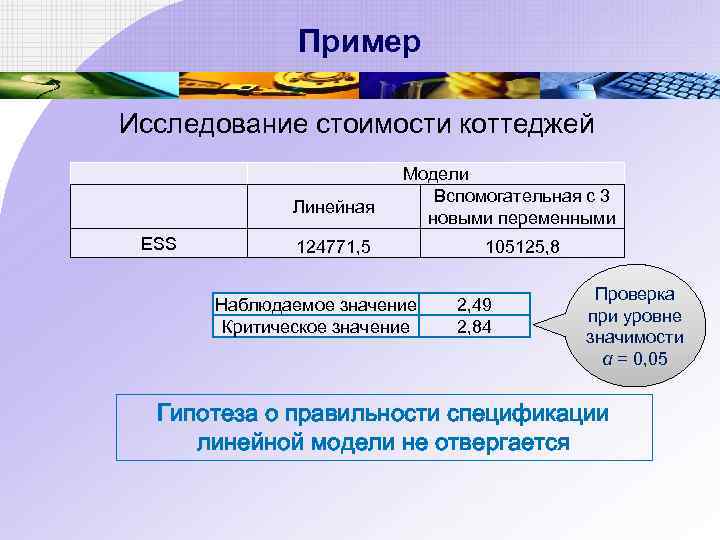Пример Исследование стоимости коттеджей Линейная ESS Модели Вспомогательная с 3 новыми переменными 124771, 5 Наблюдаемое значение Критическое значение 105125, 8 2, 49 2, 84 Проверка при уровне значимости α = 0, 05 Гипотеза о правильности спецификации линейной модели не отвергается

МУЛЬТИКОЛЛИНЕАРНОСТЬ

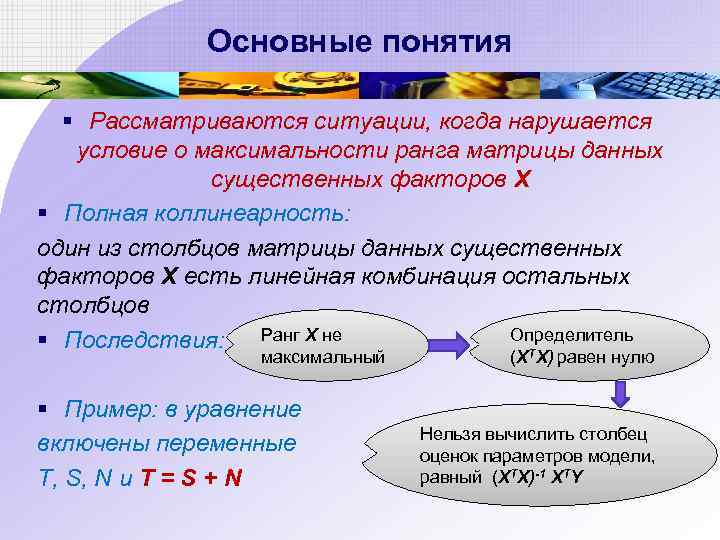Основные понятия § Рассматриваются ситуации, когда нарушается условие о максимальности ранга матрицы данных существенных факторов Х § Полная коллинеарность: один из столбцов матрицы данных существенных факторов X есть линейная комбинация остальных столбцов Ранг Х не Определитель § Последствия: Т максимальный § Пример: в уравнение включены переменные Т, S, N и T = S + N (Х Х) равен нулю Нельзя вычислить столбец оценок параметров модели, равный (ХТХ)-1 ХТY

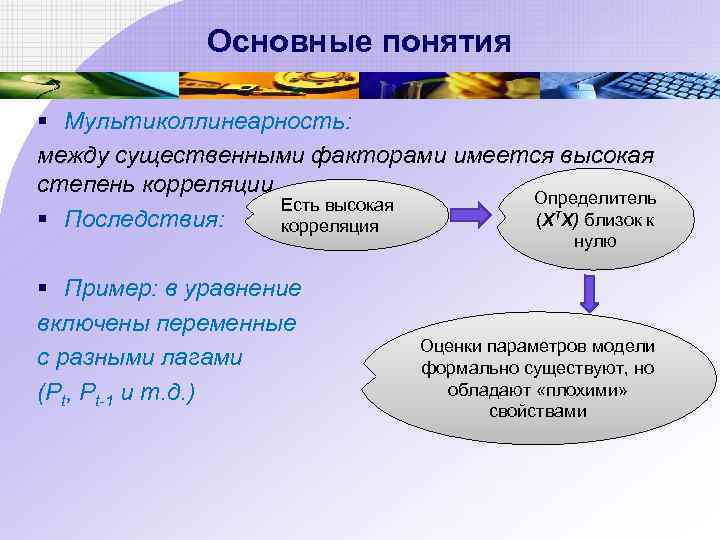Основные понятия § Мультиколлинеарность: между существенными факторами имеется высокая степень корреляции Определитель Есть высокая (ХТХ) близок к § Последствия: корреляция нулю § Пример: в уравнение включены переменные с разными лагами (Pt, Pt-1 и т. д. ) Оценки параметров модели формально существуют, но обладают «плохими» свойствами

Характерные признаки мульколлинеарности § Оценки коэффициентов имеют неправильные с точки зрения теории знаки или неоправданно большие значения § Оценки имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой с высоким коэффициентом детерминации § Небольшое изменение исходных данных приводит к существенному изменению оценок коэффициентов модели Например, добавление новых наблюдений

Коэффициент роста дисперсии § Коэффициент увеличения дисперсии (variance inflation factor, VIF): Показатель наличия мультиколлинеарности § R 2 j — коэффициент детерминации в модели линейной регрессии, описывающей зависимость существенного фактора с номером j от остальных независимых переменных § Коэффициент показывает, во сколько раз дисперсия оценки параметра больше «идеальной» (если бы мультиколлинеарности не было)

Коэффициент роста дисперсии § Практическое применение § Если все значения VIF меньше 4, то считается, что в модели мульколлинеарность не обнаружена § Если хотя бы одно значение VIF больше 4, то в модели возможно наличие мультиколлинеарности § При наличии значений VIF больше 10, считается, что в модели имеется мульколлинеарность

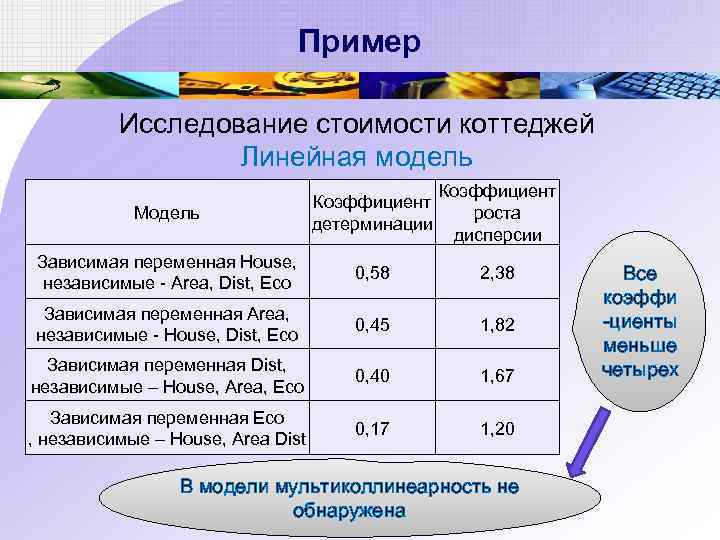Пример Исследование стоимости коттеджей Линейная модель Модель Коэффициент детерминации Коэффициент роста дисперсии Зависимая переменная House, независимые - Area, Dist, Eco 0, 58 2, 38 Зависимая переменная Area, независимые - House, Dist, Eco 0, 45 1, 82 Зависимая переменная Dist, независимые – House, Area, Eco 0, 40 1, 67 Зависимая переменная Eco , независимые – House, Area Dist 0, 17 1, 20 В модели мультиколлинеарность не обнаружена Все коэффи -циенты меньше четырех

ГЕТЕРОСКЕДАСТИЧНОСТЬ

Основные понятия § Рассматриваются ситуации, когда нарушается условие о том, что дисперсии сериальных ошибок должны быть одинаковыми § Гетероскедастичность: по крайней мере у двух сериальных ошибок дисперсии различны § Причины появления: значения переменных в уравнении регрессии сильно отличаются в разных наблюдениях § Пример: при исследовании зависимости прибыли предприятия от размера основного фонда колебание прибыли для больших предприятий выше, чем для малых

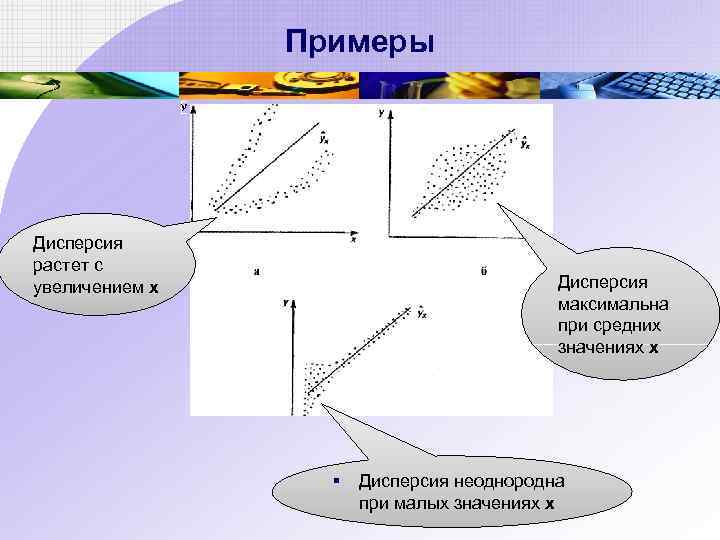Примеры Дисперсия растет с увеличением х Дисперсия максимальна при средних значениях х § Дисперсия неоднородна при малых значениях х

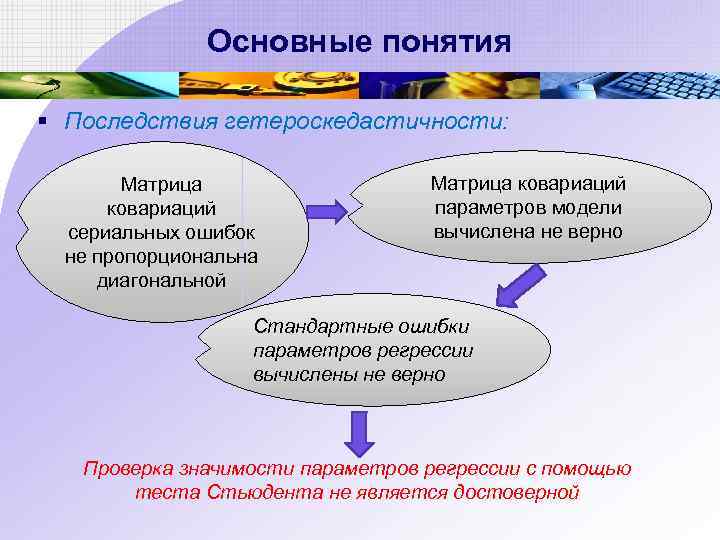Основные понятия § Последствия гетероскедастичности: Матрица ковариаций сериальных ошибок не пропорциональна диагональной Матрица ковариаций параметров модели вычислена не верно Стандартные ошибки параметров регрессии вычислены не верно Проверка значимости параметров регрессии с помощью теста Стьюдента не является достоверной

ТЕСТЫ НА ГЕТЕРОСКЕДАСТИЧНОСТЬ

Тест Уайта (White) – универсальный, он проверяет наличие гетероскедастичности любого вида Предварительный этап § вычислить характеристики вспомогательной модели, в которой: ü значения зависимой переменной − остатки проверяемой модели ü независимые переменные − прежние переменные и их всевозможные попарные произведения R 2 – коэффициент детерминации вспомогательной модели n – объем выборки m – число регрессоров вспомогательной модели

Тест Уайта § Основная гипотеза – в модели нет гетероскедастичности § Альтернативная – в модели есть гетероскедастичность § Наблюдаемое значение: Проверка § Критическое значение: квантиль при заданном уровня 1– α распределения хи-квадрат уровне с m – 1 степенью свободы § Выводы: если наблюдаемое больше значимости α критического, то в модели есть гетероскедастичность (с возможной 100α%-й ошибкой) если наблюдаемое меньше критического, то гипотеза об отсутствии гетероскедастичности не отвергается

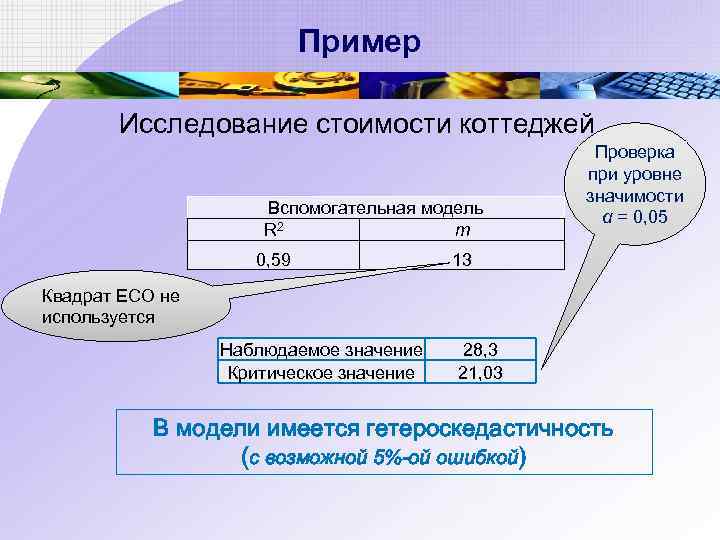Пример Исследование стоимости коттеджей Вспомогательная модель R 2 m 0, 59 Проверка при уровне значимости α = 0, 05 13 Квадрат ECO не используется Наблюдаемое значение Критическое значение 28, 3 21, 03 В модели имеется гетероскедастичность (с возможной 5%-ой ошибкой)

Тест Голдфелда–Куандта (Goldfeld - Quandt) применяется для проверки гипотезы о прямой зависимости дисперсии ошибки от величины одной из объясняющих переменных

Тест Голдфелда–Куандта Предварительный этап § упорядочить данные по возрастанию выбранной независимой переменной § исключить d средних наблюдений (примерно четверть от общего количества n) так, чтобы осталось четное число наблюдений 2 m § построить две модели: одну на основе первых m наблюдений, вторую — на основе последних m наблюдений § ESS 1 — сумма квадратов остатков первой модели § ESS 2 — сумма квадратов остатков второй модели

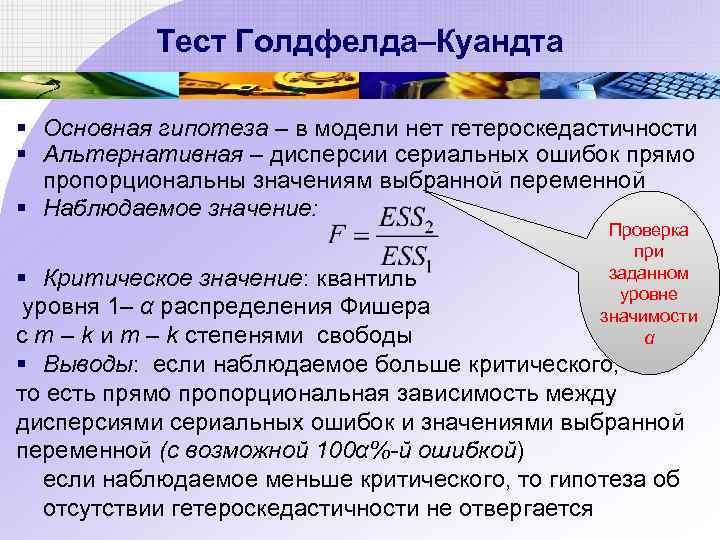Тест Голдфелда–Куандта § Основная гипотеза – в модели нет гетероскедастичности § Альтернативная – дисперсии сериальных ошибок прямо пропорциональны значениям выбранной переменной § Наблюдаемое значение: Проверка при заданном уровне значимости α § Критическое значение: квантиль уровня 1– α распределения Фишера с m – k и m – k степенями свободы § Выводы: если наблюдаемое больше критического, то есть прямо пропорциональная зависимость между дисперсиями сериальных ошибок и значениями выбранной переменной (с возможной 100α%-й ошибкой) если наблюдаемое меньше критического, то гипотеза об отсутствии гетероскедастичности не отвергается

Пример Исследование стоимости коттеджей Проверяется наличие гетероскедастичности специального вида: дисперсии сериальных ошибок прямо пропорциональны значениям переменной House n = 48 d = 12 2 m = 36 Проверка Вспомогательные модели ESS 1 ESS 2 422, 52 73929, 83 Наблюдаемое значение Критическое значение при уровне значимости α = 0, 05 174, 97 2, 576927 В модели имеется гетероскедастичность: дисперсии сериальных ошибок прямо пропорциональны значениям переменной House (с возможной 5%-ой ошибкой)

КОРРЕКЦИЯ НА ГЕТЕРОСКЕДАСТИЧНОСТЬ

Коррекция стандартных ошибок § Как сделать поправку на гетероскедастичность и «улучшить» оценки стандартных ошибок? Положительный ответ дает использование стандартных ошибок в форме Уайта или в форме Ньюи-Веста § При использовании стандартных ошибок в форме Уайта или в форме Ньюи-Веста уравнение модели не меняется! § Использование этих стандартных ошибок позволяет получить только верные выводы о значимости параметров регрессии

Метод взвешенных квадратов § Если дисперсии сериальных ошибок известны или их удается найти приближенно, то можно использовать метод взвешенных наименьших квадратов § Описание метода § Каждое уравнение спецификации модели § делим на величину σi среднего квадратического отклонения сериальной ошибки εi: § В новой модели дисперсии сериальных ошибок равны 1

Метод взвешенных квадратов § Особенности метода § Проверка различных гипотез (значимость параметров исходной модели и т. д. ) проводится с помощью вспомогательной модели § Коэффициент детерминации вспомогательной модели не может служить мерой качества модели (не выполняется теорема о сумме квадратов) § Применение метода требует знания значений (точных или приближенных) средних квадратических отклонений сериальных ошибок

ИСТИННАЯ И ЛОЖНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ

Истинная и ложная гетероскедастичность § Неверная спецификация функциональной формы модели может привести к тому, что тесты могут показывать наличие гетероскедастичности, хотя ее нет § Истинная гетероскедастичность вызывается непостоянством дисперсии случайного члена, ее зависимостью от различных факторов § Ложная гетероскедастичность вызывается ошибочной спецификацией модели регрессии

АВТОКОРРЕЛЯЦИЯ

Основные понятия § Рассматриваются ситуации, когда нарушается условие о том, что сериальные ошибки не должны коррелировать между собой § Автокорреляция: по крайней мере две сериальные ошибки коррелируют друг с другом § Автокорреляция обычно встречается при использовании временных рядов § Основная причина: не включение в уравнение какоголибо существенного фактора

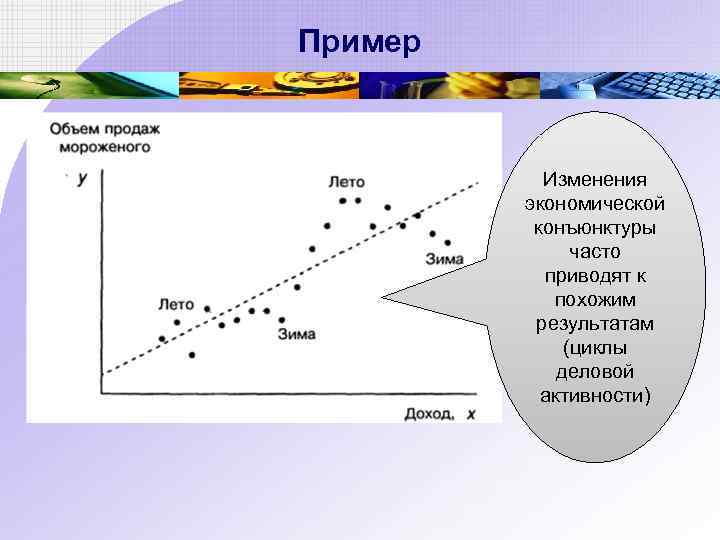Пример Изменения экономической конъюнктуры часто приводят к похожим результатам (циклы деловой активности)

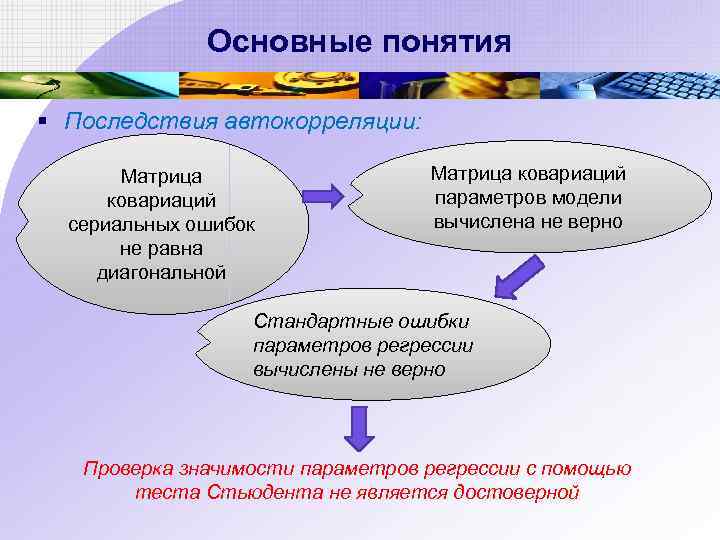Основные понятия § Последствия автокорреляции: Матрица ковариаций сериальных ошибок не равна диагональной Матрица ковариаций параметров модели вычислена не верно Стандартные ошибки параметров регрессии вычислены не верно Проверка значимости параметров регрессии с помощью теста Стьюдента не является достоверной

Авторегрессия 1 порядка § Сериальные εt ошибки образуют авторегрессионный процесс первого порядка, если εt = ρεt-1 + ut , § где ρ ─ коэффициент авторегрессии, |ρ| < 1 § ut ─ случайные величины, не коррелирующие между собой и с сериальными ошибками § Положительная автокорреляция 1 порядка: 0 < ρ <1 § Отрицательная автокорреляция 1 порядка : − 1 < ρ <0

Тест Дарбина–Уотсона Для обнаружения автокорреляции первого порядка используется тест Дарбина–Уотсона (Durbin & Watson, 1951) § Основная гипотеза – в модели нет автокорреляции § Альтернативная – в модели есть положительная автокорреляция первого порядка Проверка § Наблюдаемое значение: при § Критическая область: определяется нижней dl и верхней du границами (вычисляются по специальным таблицам) Выводы DW < dl dl < DW < d. U Основная гипотеза отвергается Зона (с возможной 100α%-й неопределенности ошибкой) заданном уровне значимости α DW > d. U Основная гипотеза не отвергается

Пример Зависимость расходов на транспорт от дохода (США, 1946 -2002 годы) Линейная модель Проверка Наблюдаемое значение 0, 23 Критические значения Нижняя граница 1, 45 Верхняя граница 1, 64 В модели имеется положительная автокорреляция первого порядка (с возможной 5%-ой ошибкой) при уровне значимости α = 0, 05

УСТРАНЕНИЕ АВТОКОРРЕЛЯЦИИ

Использование коэффициента авторегрессии Рассматривается случай наличия автокорреляции первого порядка Если коэффициент авторегрессии известен или известно его приближенное значение, то можно использовать частный случай обобщенного метода наименьших квадратов

Использование коэффициента авторегрессии § Описание метода § Каждое уравнение спецификации модели в момент времени t § сложим с аналогичным уравнением в момент времени t -1, умноженным на величину ρ § Учитывая, что εt = ρεt-1 + ut , получаем: § В новой модели сериальные ошибки не коррелируют друг с другом и здесь можно использовать обычный метод наименьших квадратов

Оценка коэффициента авторегресии § Есть разные способы нахождения приближенного значения коэффициента авторегрессии Процедура Кохрейна-Оркатта (Соchrane–Оrcutt) § Вычисляется значение ρ как коэффициента уравнения модели et = ρet-1 + ut (et ─ остатки в исходной модели) § Для найденного значения ρ вычисляются остатки в модели § С помощью вычисленных остатков находится новое значение ρ как коэффициента уравнения модели et = ρet-1 + ut § Процесс обычно заканчивается, когда очередное значение ρ мало отличается от предыдущего