Разделение секрета Пример Представьте что Вы

Разделение секрета

Пример • Представьте, что Вы и Ваш друг случайно нашли карту, которая, как вы уверены, приведет вас на остров, полный сокровищ. • Вы и Ваш друг должны возвратиться домой и приготовиться к полному приключений путешествию за большой удачей. • У кого будет храниться карта?

Пример • Предположим, что Вы и Ваш так называемый приятель на самом деле не доверяете другу и каждый из вас боится, что другой, имея карту, все сделает самостоятельно и заберет сокровища себе. • Необходимо разработать схему, при которой ни один из участников путешествия не сможет самостоятельно достичь цели, но только вместе. • Что Вы могли бы предложить?

Пример • Разорвать карту на две части, так что только сложив две части карты, можно было найти сокровища. • Теперь можно спокойно идти домой и собираться в путешествие будучи уверенным, что ни один участник не отправится без другого. • Этот пример иллюстрирует базовую концепцию протокола разделения секрета.

Обобщение • Пусть задан секрет s, мы хотели бы, чтобы n участников разделяли секрет таким образом, чтобы выполнялись следующие свойства: – – • Все n участников могут собраться вместе и восстановить s. Меньшее, чем n участников не могут восстановить s. В примере с картой, s – это карта, тогда как Вы и Ваш приятель – два участника, разделяющие секрет.

Обобщение • В общем случае, чтобы достичь такого разделения, мы разбиваем секрет на n частей s 1, s 2, . . . , sn и передаем одну часть каждому участнику. • Каждая часть называется долей, проекцией (share, shadow). • На самом деле мы рассмотрели специальный случай разделения секрета (называемый в литературе secret splitting). • При таком разделении возникают некоторые проблемы, видные из другого примера. 6

Другой пример • Два совладельца драгоценности хотят положить ее на хранение в сейф. • Сейф современный, с цифровым замком на 16 цифр. • Так как совладельцы не доверяют другу, то они хотят закрыть сейф таким образом, чтобы они могли открыть его вместе, но никак не порознь.

Другой пример • Для этого они приглашают третье лицо, называемое дилером (доверенное лицо), которому они оба доверяют (например, потому что оно не получит больше доступ к сейфу).

Другой пример • Доверенное лицо – дилер (trusted third party)

Другой пример • Дилер случайно выбирает 16 цифр в качестве «ключа» , чтобы закрыть сейф, и затем сообщает первому совладельцу втайне от второго первые 8 цифр «ключа» , а второму совладельцу втайне от первого — последние 8 цифр «ключа» .

Другой пример • Такой способ представляется с точки здравого смысла оптимальным, ведь каждый из совладельцев получил «полключа» и что может быть лучше? ! • Недостатком является то, что любой из совладельцев, оставшись наедине с сейфом, может за пару минут найти недостающие «полключа» с помощью несложного устройства, перебирающего ключи со скоростью 1 МГц.

Проблема: частичное раскрытие информации Наивный путь разделения секрета путем разрывания карты на части или разрывания пароля на несколько частей приводит к частичному раскрытию информации, что неприемлемо в некоторых случаях. 12

Другой пример • Кажется, что единственный выход - в увеличении размера «ключа» , скажем, вдвое. Но есть другой, математический выход, опровергающий соображения здравого смысла.

Другой пример (продолжение) • Дилер независимо выбирает две случайные последовательности по 16 цифр в каждой, сообщает каждому из совладельцев втайне от другого «его» последовательность, а в качестве «ключа» , чтобы закрыть сейф, использует последовательность, полученную сложением по модулю 10 соответствующих цифр двух выбранных последовательностей.

Другой пример • Очевидно, что для каждого из совладельцев все возможные «ключи» одинаково вероятны и остается только перебирать их, что потребует в среднем более полутора лет для устройства, перебирающего ключи со скоростью 100 МГц.

Некоторые выводы • Последний способ разделения секрета обладает двумя свойствами. – Секрет можно восстановить по двум долям – Секрет трудно восстановить, если долей секрета меньше двух (нет утечки информации) 16

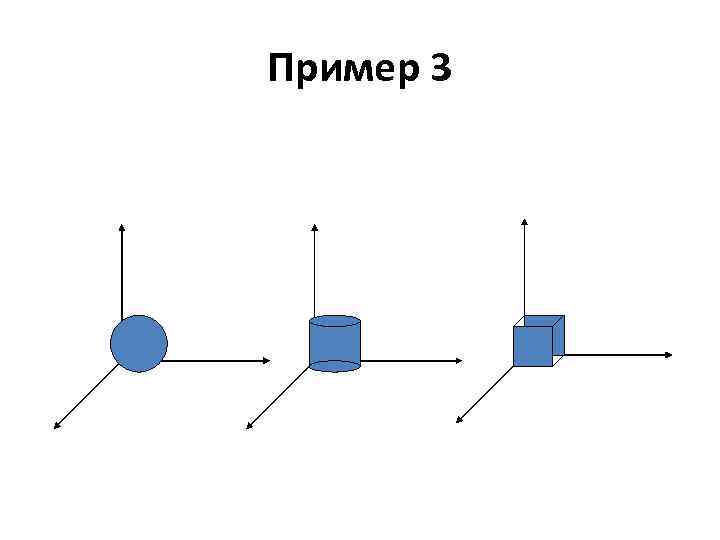
Пример 3 • Множество S всех возможных секретов состоит из шара; куба, ребра которого параллельны осям координат; цилиндра, образующие которого параллельны оси Z. • При этом диаметры шара и основания цилиндра, и длины ребра куба и образующей цилиндра, равны.

Пример 3

Пример 3 • Первый участник получает в качестве своей «доли» секрета его проекцию на плоскость XY, а второй — на плоскость XZ. • Ясно, что вместе они однозначно восстановят секрет, а порознь - не могут.

Пример 3 Однако, эта СРС не является совершенной, так как любой из участников получает информацию о секрете, оставляя только два значения секрета как возможные при данной проекции (например, если проекция — квадрат, то шар невозможен).

История • История СРС начинается с 1979 года, когда эта проблема была поставлена и во многом решена Г. Блейкли и А. Шамиром для случая пороговых (n, t)-СРС (т. е. восстановить секрет могут любые t или более участников).

Еще обобщение : (n, t) пороговые схемы (Shamir) • • • Пусть задан секрет s, который должен разделяться n участниками, так что выполняются следующие условия: достижимость: не менее t участников могут восстановить секрет s. секретность: менее t участников не получают никакой информации о секрете s. 22

Линейное разделение секрета Пусть GF(q) - конечное поле из q элементов (например, q = р - простое число), q>>n. Сопоставим n участникам n различных ненулевых элементов поля (ID) Пусть имеется секрет

Линейное разделение секрета При распределении секрета дилер генерирует k-1 независимых равномерно распределенных на GF(q) случайных величин и строит многочлен

Линейное разделение секрета Затем дилер посылает участнику с номером j (j = 1, . . . , n) «его» проекцию секрета.

Линейное разделение секрета 26

Линейное разделение секрета Поскольку любой многочлен степени не более t - 1 однозначно восстанавливается по его значениям в произвольных t точках (например, по интерполяционной формуле Лагранжа), то любые t участников вместе могут восстановить многочлен f(x) и, следовательно, найти значение секрета как

Линейное разделение секрета Коэффициенты неизвестного многочлена f(x) степени не более t-1 можно определить с помощью пар по интерполяционной формуле Лагранжа

Линейное разделение секрета

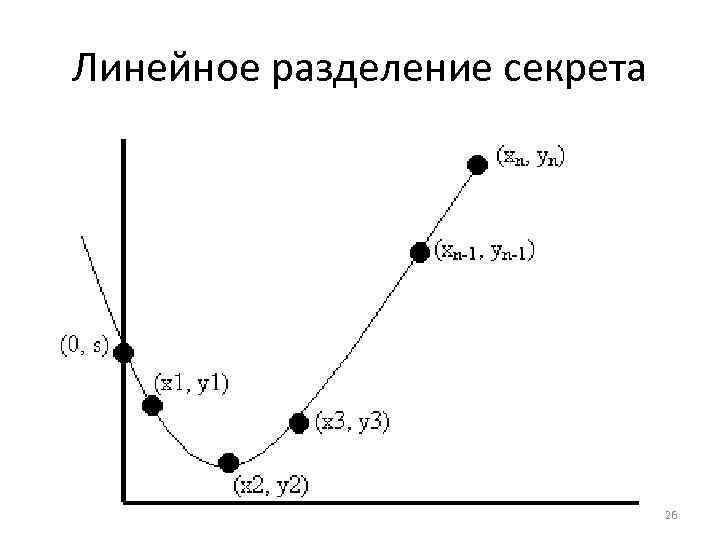
Линейное разделение секрета Если участников < t, то для любых полученных ими значений проекций и любого значения секрета им нужно угадать еще одну проекцию секрета, а это то же самое, что угадать сам секрет.

Пример: (5, 3) пороговая схема • Секрет k=13, выбирается из множества элементов GF(17): {0, 1, 2, …, 16} Bob Alice ID 1=1 (1, 8) ID 2=2 Ken Jesse ID 3=3 (3, 10) Интерполяционный многочлен Лагранжа ID 4=4 Eva ID 5=5 (5, 11)

Постановка проблемы • Неформально говоря, «схема, разделяющая секрет» (СРС) позволяет «распределить» секрет между n участниками таким образом, чтобы заранее заданные разрешенные множества участников могли однозначно восстановить секрет (совокупность этих множеств называется структурой доступа), а неразрешенные — не получали никакой дополнительной к имеющейся априорной информации о возможном значении секрета. СРС с последним свойством называются совершенными.

Постановка проблемы • Цель СРС состоит в том, чтобы: • а) участники из разрешенного множества вместе могли бы однозначно восстановить значение секрета • б) участники, образующие неразрешенное множество не могли бы получить дополнительную информацию о секрете.

Применения протоколов разделения секрета • • Коллективная собственность Коллективная цифровая подпись Кворум Протоколы голосования

Формальная математическая модель • Имеется n+1 множество и распределение вероятностей Р на их декартовом произведении. Соответствующие случайные величины обозначаются через. Имеется также некоторое множество подмножества {1, . . . , n}, называемое структурой доступа.

Формальная математическая модель • Определение 1. Пара (Р, S) называется совершенной вероятностной СРС, реализующей структуру доступа , если