РАЗДЕЛ X ТЕОРИЯ ВЕРОЯТНОСТЕЙ Тема 1 Введение в

РАЗДЕЛ X. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Тема 1. Введение в теорию вероятностей

n Опр. 1. Теория вероятностей – это математическая наука, изучающая закономерности случайных явлений.

Особенности изучаемых явлений: n n 1. Опыты в одних и тех же условиях можно повторять сколько угодно раз, хотя бы мысленно. 2. Исход каждого опыта заранее не известен и может изменятся от опыта к опыту.

n Опр. 2. Математическая статистика – раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдения для того чтобы выявить статистические законы.

Задачи Де Мере: n n 1. Игральная кость подбрасывается четыре раза. На что нужно сделать ставку: «хотя бы один раз выпадет 6» или « 6 не выпадет ни разу» ? 2. Две игральные кости подбрасываются 24 раза. На что нужно сделать ставку: «хотя бы один раз выпадет две 6» или « 6 не выпадет ни разу» ?

Области применения теории вероятностей и математической статистики: ¨ теория надежности; ¨ теория катастроф; ¨ теория массового обслуживания; ¨ теория ошибок наблюдения; ¨ теория автоматического управления; ¨ теория игр; ¨ наука об эффективности боевых действий; ¨ астрономия и теоретическая физика; ¨ медицина и генетика; ¨ социология и психология; ¨ лингвистика; ¨ информационная безопасность.

РАЗДЕЛ X. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Тема 2. Классическое определение вероятности

§ 1. События

n n n n Опр. 1. Случайным событием называют любой факт, который в результате опыта может произойти или не произойти. Опр. 2. Событие называется достоверным, если в результате опыта оно обязательно должно произойти. Опр. 3. Событие называется невозможным, если в результате опыта оно никогда не может произойти. Опр. 4. Два события А и В называются несовместными, если в результате опыта они не могут произойти одновременно. В противном случае события называются совместными. Опр. 5. Несколько событий называются равновозможными, если в результате опыта ни одно из них не должно происходить чаще других. Опр. 6. Если в результате опыта обязательно произойдет одно и только одно из нескольких событий, то говорят, что эти события образуют полную группу. Опр. 7. Если события в полной группе равновозможны, тот они называются элементарными исходами опыта и обозначаются ω. Опр. 8. Элементарный исход называется благоприятным для события А, если в результате опыта при появлении такого исхода обязательно произойдет событие А.

§ 2. Классическое определение вероятности

n Опр. По классическому определению вероятности вероятность события А равна отношению числа благоприятных элементарных исходов к общему числу элементарных исходов: n где Р(А) – вероятность события А, m – число благоприятных элементарных исходов, n – число всех элементарных исходов.

Алгоритм расчёта классической вероятности события: 1. 2. 3. 4. 5. Четко представить, в чем состоит опыт, в каких условиях выполняется. Представить, в чем состоят элементарные исходы, которые будут равновозможны и в результате опыта обязательно произойдет один и только один из них. Подсчитать все элементарные исходы. Выбрать среди элементарных исходов благоприятные для события А и подсчитать их. Найти вероятность события А по классическому определению.

Свойства вероятностей: n Пусть А – некоторое событие, тогда n где Ω - достоверное событие. Р(Ø) = 0, где Ø – невозможное событие. n

§ 3. Элементы комбинаторики

n Опр. 1. Комбинаторика – это раздел математики, изучающий методы решения задач на подсчёт числа различных комбинаций из объектов, выбранных из некоторой совокупности.

Основные комбинаторные правила: n n Правило суммы: если один объект можно выбрать из совокупности m способами, а другой – n способами, то выбрать либо один объект, либо другой можно m+n способами. Правило произведения: если один объект можно выбрать из совокупности m способами, а после этого выбора другой объект выбрать n способами, то выбрать и тот, и другой в указанном порядке можно mn способами.

n n Опр. 2. Перестановками называют комбинации, составленные из n различных объектов и отличающихся только порядком этих объектов. Число всех перестановок из n объектов обозначают Рn. Теорема. 1. Число всех перестановок Pn данного количества объектов n равно n!.

n n Опр. 3. Размещениями из n элементов по m называют комбинации, составленные из m объектов и отличающиеся составом или порядком этих объектов, причём данные объекты выбираются из совокупности различных n объектов. Число размещений из n по m обозначают Теорема. 2. Число размещений

n n Опр. 4. Сочетаниями из n по m называют комбинации, составленные из m объектов, эти объекты выбираются из совокупности n различных объектов, причём важен только состав выбранной совокупности. Число сочетаний из n по m обозначают. Теорема. 3. Число сочетаний из n по m равно: .

РАЗДЕЛ X. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Тема 3. Геометрическое и статистическое определения вероятности

§ 1. Геометрическое определение вероятности

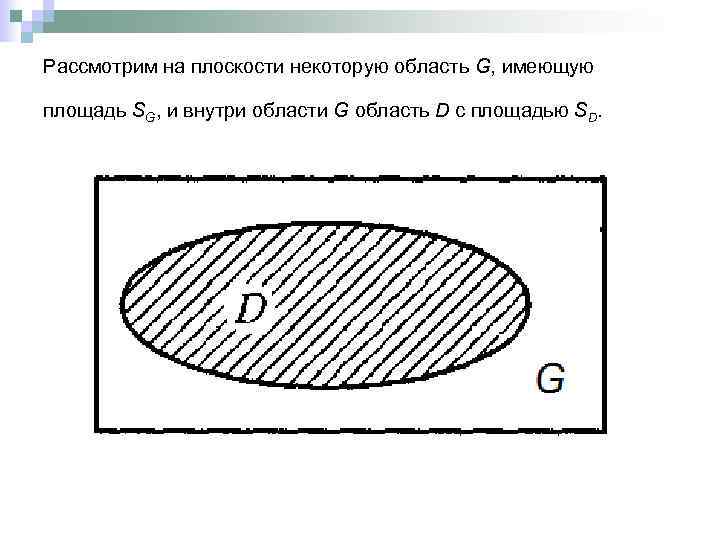Рассмотрим на плоскости некоторую область G, имеющую площадь SG, и внутри области G область D с площадью SD.

Пусть событие А – брошенная точка попадет в область D. Опр. 1. Геометрической вероятностью события А называется отношение площади D к площади области G. n Геометрическое определение вероятности события применимо и в случае, когда области G и D обе линейные или объемные. n

§ 2. Классическая задача «о встрече»

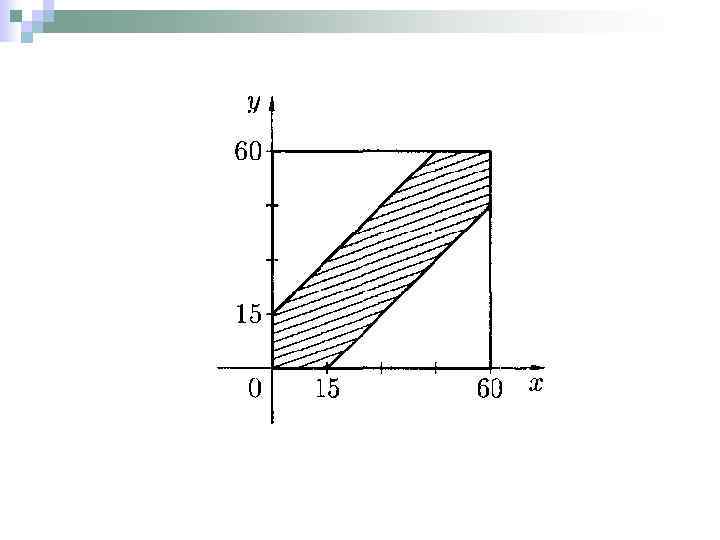
n Задача. Два человека договорились о встрече между 9 и 10 часами утра. Пришедший первым ждет второго в течении 15 минут, после чего уходит (если не встретились). Найти вероятность того, что встреча состоится, если каждый наудачу выбирает время своего прихода.

§ 3. Статистическое определение вероятности

n n n Опр. 1. Статистическая устойчивость: с увеличением числа опытов относительная частота появления события принимает значения, близкие к некоторому постоянному числу. Опр. 2. Статистической вероятностью события называется относительная частота появления этого события в проведённых опытах: где n* – число проведённых опытов, m* – число опытов, в которых событие А появилось.

РАЗДЕЛ X. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Тема 4. Приемы вычисления вероятности составного события

§ 1. Операции над случайными событиями

n n n Опр. 1. Суммой нескольких событий называется событие, которое состоится, если в результате опыта произойдет хотя бы одно из них. Обозначаем А+В. Замечания: Если события А и В совместны, то их сумма состоит в появлении или события А, или события В, или обоих вместе. Если события А и В несовместны, то их сумма состоит в появлении или А или В. Сумма событий, составляющих полную группу, является событием достоверным.

n n n Опр. 2. Произведением нескольких событий называется событие, которое состоится, если в результате опыта произойдут все эти события. Обозначаем АВ. Замечание: Если события А и В несовместны, то АВ = Ø. Опр. 3. Разностью событий А и В называется событие, которое состоится, если в результате опыта событие А произойдёт, а событие В – нет. Обозначаем А – В.

§ 2. Свойства операций над событиями. Изображение операций над событиями с помощью диаграмм Эйлера

Операции над событиями обладают следующими свойствами: n n n А+B=B+A, A∙B=B∙A (переместительное); (A+B)∙C=A∙C+B∙C, A∙B+C=(A+C)∙(B+C) (распределительное); (A+B)+C=A+(B+C), (A∙B)∙C=A(B∙C) (сочетательное); А+А=А, А∙А=А; А+Ω= Ω, А∙ Ω=А;

Операции над событиями обладают следующими свойствами:

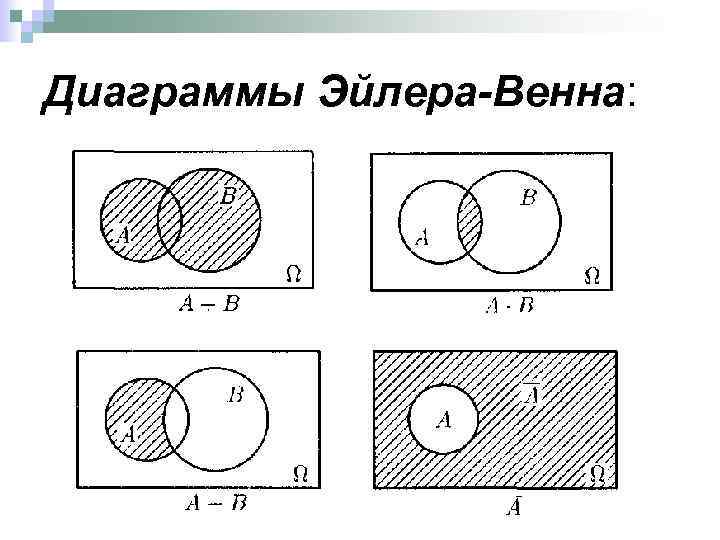Диаграммы Эйлера-Венна:

§ 3. Теоремы сложения вероятностей

Теорема 1. Вероятность суммы несовместных событий равна сумме вероятностей этих событий: Р(А + В) = Р(А) + Р(В), А и В несовместны. n Теорема 2. Вероятность суммы совместных событий А и В вычисляется по формуле: Р(А + В) = Р(А) + Р(В) – Р(АВ). n Замечание: Вероятность суммы трёх совместных событий вычисляется по формуле: Р(А+В+С)=Р(А)+Р(В)+Р(С)–Р(АВ)–Р(ВС)–Р(АС)+Р(АВС). n Теорема 3. Вероятность суммы событий, составляющих полную группу равна 1. n Теорема 4. Вероятность события, противоположного А равна 1–Р(А). n

§ 4. Теоремы умножения вероятностей

n n Опр. 1. Вероятность события В, найденная при условии, что перед этим произошло событие А, называется условной вероятностью события В и обозначается Р(В/А). Опр. 2. События А и В называют независимыми, если вероятность любого из них не изменится оттого, что произойдёт другое: Р(В) = Р(В/А). В противном случае события называются зависимыми.

Пример. События: n А – появление карты красной масти при извлечении одной карты из колоды, n В – появление туза, n С – появление туза бубен, n А/В – появление карты красной масти, если уже известно, что это туз, n А/С – появление карты красной масти, если уже известно, что это туз бубен, n В/А – появление карты туз, если известно, что она красная, n В/С – появление туза, если уже известно, что извлеченная карта – туз бубен, n С/А – появление туза бубен, если известно, что извлечена красная карта, n С/В – появление туза бубен, при условии, что извлечён туз.

n n Теорема. 1. Вероятность произведения зависимых событий А и В равна произведению вероятности события А на условную вероятность события В, вычисленную при условии, что событие А произошло: Р(АВ) = Р(А)·Р(В/А), А и В зависимы. Теорема. 2. Вероятность произведения независимых событий А и В равна произведению вероятностей событий А и В: Р(АВ) = Р(А)·Р(В), А и В независимы.

§ 5. Схема решения задач на теоремы сложения и умножения событий

n n n Осмыслить условие задачи и записать краткое условие. Ввести сложное событие, вероятность которого требуется найти и простые события, из которых состоит сложное. Выразить сложное событие через простые с помощью операций сложение и умножение. ¨ ¨ n Если при этом используется сложение событий, то выбирается одна из теорем о сложении, в зависимости от условий задачи. Если используется умножение событий, то выбирается подходящая теорема об умножении событий. Окончательная формула должна состоять из вероятностей простых событий, которые известны или легко вычисляются по условию задачи.

§ 6. Формула полной вероятности. Формула Байеса

Задача. n На столе лежит 25 экзаменационных билетов, среди них 20 легких и 5 трудных. Студент входит в аудиторию вторым по счёту и берет билет. Какова вероятность, что ему достанется легкий билет?

n Теорема о полной вероятности. Если событие А может произойти только после появления одного из событий (гипотез) Н 1, Н 2, … , Hn, составляющих полную группу, то вероятность события А определяется по формуле:

n Теорема формула Байеса. Если выполняются условия теоремы о полной вероятности, то условная вероятность гипотезы Нi при условии наступления события А определяется формулой:

РАЗДЕЛ X. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Тема 5. Независимые повторные испытания

n n Опр. 1. Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода — «успех» и «неудача» , при этом «успех» в одном испытании происходит с вероятность р [0, 1], «неудача» — с вероятностью q=1 -p. Теорема Бернулли. Пусть в каждом из n независимых испытаниях событие А наступает с вероятностью р и не наступает с вероятностью q=1 -p. Тогда вероятность, что в этих испытаниях событие А наступит ровно m раз равна

n Теорема 1. В n испытаниях схемы Бернулли с вероятностью успеха p наиболее вероятным числом успехов является: ¨ a) единственное число k 0=[np+p], если число np+p не целое; ¨ б) два числа k 0=np+p и k 0 -1=np+ p-1, если число np+p целое. n Теорема 1’. В n испытаниях схемы Бернулли с вероятностью успеха p наиболее вероятным числом успехов является число k 0 такое, что np-q k 0 np+p.

n n Теорема Пуассона. Пусть n→∞ , p→ 0 так, что np→ λ > 0. Тогда для любого k≥ 0 вероятность получить k успехов в n испытаниях схемы Бернулли с вероятностью успеха p стремится к величине Замечание. По схеме Бернулли р=const, а для формулы Пуассона p→ 0. Тем не менее с хорошей точностью можно считать, что если р=const и мало, n – велико, np=λ=const 10, то

n Локальная теорема Муавра – Лапласа. Если в каждом из n независимых испытаниях событие А наступает с постоянной вероятностью р, то вероятность что данное событие наступит ровно m раз вычисляется по формуле n Замечания. ¨ 1. Формула дает допустимую погрешность при npq≥ 20. ¨ 2. φ(х) – четная, монотонно убывающая при х→∞ функция. Если x>4, то φ(х)≈0.

n Интегральная теорема Муавра – Лапласа. Если в каждом из n независимых испытаниях событие А наступает с постоянной вероятностью р, то вероятность что данное событие наступит m 1 m m 2 раз вычисляется по формуле n Замечания. ¨ 1. Формула дает допустимую погрешность при npq≥ 20. ¨ 2. Ф(х) – нечетная, монотонно возрастающая при х→∞ функция. Если x>4, то Ф(х)≈0, 5.

РАЗДЕЛ X. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Тема 6. Дискретные случайные величины

§ 1. Дискретная случайная величина. Закон её распределения

n n n n Опр. 1. Случайная величина – это переменная, которая в результате опыта принимает одно из множества возможных значений, заранее не известно какое. Примеры: Число появлений герба при трёх бросках монеты. Дальность полёта снаряда. Расход электроэнергии потребителем за месяц. Ошибка измерения расстояния. Время безотказной работы прибора.

n n n Опр. 2. Случайная величина называется дискретной (ДСВ), если её значения можно перенумеровать. Например, число появлений герба при трёх бросках монеты есть дискретная случайная величина, т. к. она может принимать значения 1, 2 или 3, эти значения можно перенумеровать. Дальность полёта снаряда не является дискретной случайной величиной, т. к. она может принимать значения из некоторого промежутка, и их перенумеровать нельзя. Замечание: У ДСВ может быть конечное множество значений (напр. , число выигравших лотерейных билетов среди купленных) и бесконечное, но счетное (напр. , число произведённых выстрелов до первого попадания, т. к. теоретически это число может быть сколь угодно большим).

Формы закона распределения: n I. Табличная форма закона распределения.

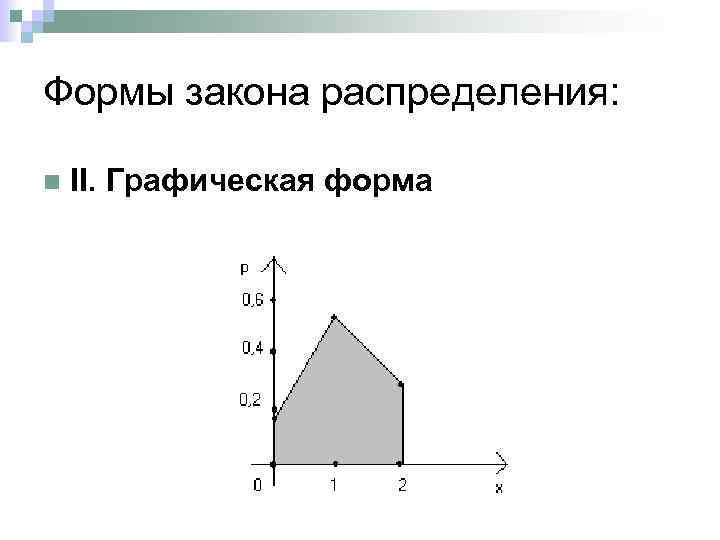Формы закона распределения: n II. Графическая форма

Опр. 4. Функцией распределения случайной величины Х называется функция F(х) : R [0, 1], при каждом x R равная F(х) = P(Х < x). Функция распределения F(х) обладает следующими свойствами: n 1) функция распределения F(х) не убывает: если х1 < x 2 то F(x 1)< F(x 2); n 2) существуют пределы и n 3) функция распределения F(x) непрерывна слева: n 4) в любой точке х0 разница F(х0+0) - F(х0) равна P(Х = х0); Следствие. Если функция распределения F(x) непрерывна в точке х0, то P(Х=х0)=0; n 5) для любой случайной величины Х имеет место равенство P(а Х

§ 2. Операции над дискретными случайными величинами

n n Опр. 1. Две случайные величины называются независимыми, если закон распределения одной не зависит от того, какие возможные значения приняла другая величина. Опр. 2. Суммой (произведением) постоянного числа с=const≠ 0 и ДСВ Х называется ДСВ, которая принимает все возможные значения с+хi (с·хi) с теми же вероятностями рi. Опр. 3. Степенью ДСВ Х с показателем s называется ДСВ, которая принимает все возможные значения хis с теми же вероятностями рi. Опр. 4. Суммой (разностью или произведением) ДСВ Х и У называется ДСВ, которая принимает все возможные значения хi+уi (хi-уi или хi·уi) с теми же вероятностями рij.

§ 3. Числовые характеристики ДСВ, их смысл и свойства

n Опр. 1. Математическим ожиданием случайной величины называют сумму произведений всех её значений на соответствующие вероятности: Свойства математического ожидания: 1. М(С) = С, если C = const; 2. М(СХ) = СМ(Х); 3. М(Х±Y) = M(X) ±M(Y); 4. М(Х·Y) = M(X)·M(Y), если X, Y – независимые случайные величины.

n Опр. 2. Дисперсией случайной величины называют математическое ожидание квадрата отклонения СВ от математического ожидания: Свойства дисперсии: 1. D(C) = 0; 2. D(CX) = C 2 D(X); 3. D(X) = M(X 2) – M 2(X).

n n Опр. 3. Среднее квадратическое отклонение – это арифметическое значение квадратного корня из дисперсии: σ(Х) = Опр. 4. Модой случайной величины называют её наиболее вероятное значение. Свойства моды дискретной случайной величины: n n Мо (С) не существует; Некоторые случайные величины полимодальны; Мо(СХ) = СМо(Х); В общем случае Мо(Х ±У)≠ Мо(Х) ± Мо(У).

§ 4. Основные законы распределения дискретных случайных величин

Вырожденное распределение.

Распределение Бернулли.

Биномиальное распределение.

Геометрическое распределение.

Распределение Пуассона.

РАЗДЕЛ X. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Тема 7. Непрерывные случайные величины

§ 1. Непрерывные случайные величины. Дифференциальная и интегральная функции распределения непрерывной случайной величины

n n n Опр. 1. Случайная величина Х называется непрерывной (НСВ), если принимаемые ею значения нельзя перенумеровать. Теорема. Вероятность того, что НСВ примет конкретное отдельное значение равна 0. Следствие. Вероятность того, что НСВ попадет в некоторый промежуток не зависит от того открытый он или закрытый.

Свойства интегральной функции распределения: 1. 0 F(x) 1; 2. Функция распределения есть неубывающая функция на всей числовой оси; 3. Вероятность попадания случайной величины в промежуток [α, β] равна приращению интегральной функции на этом промежутке: P(α X β)=F(β)-F(α); 4. Интегральная функция распределения НСВ непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек.

n Опр. 2. Дифференциальной функцией НСВ (плотностью вероятности) называется производная от её интегральной функции: f(x)= F’(x). Свойства дифференциальной функции распределения: n n f(x) ≥ 0; Вероятность попадания значений НСВ в промежуток от α до β равна n n n Геометрически интегральная функция распределения есть площадь криволинейной трапеции, ограниченной кривой дифференциальной функции распределения, в той её части, которая лежит левее х.

§ 2. Математическое ожидание и дисперсия НСВ

n Математическое ожидание НСВ вычисляется по формуле n Дисперсия НСВ находится по формуле n Модой НСВ называется значение НСВ, в которой f(х) имеет max. n Медианой НСВ Х называется такое значение, при котором Р[Х

§ 3. Основные законы распределения непрерывной случайной величины

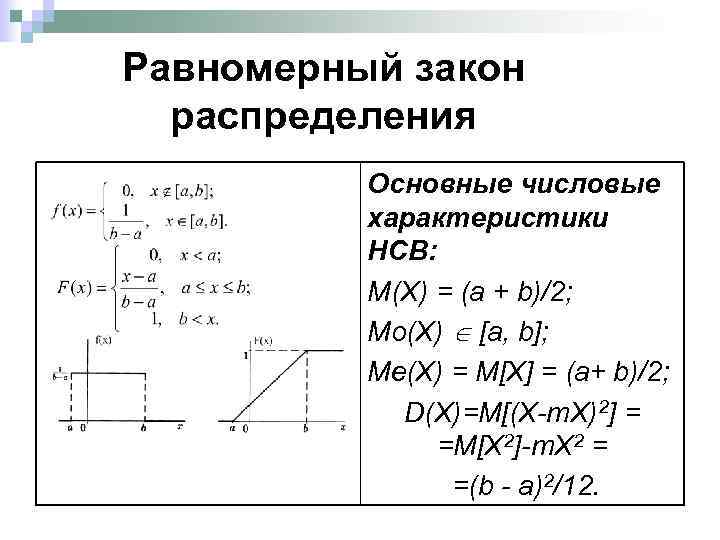Равномерный закон распределения Основные числовые характеристики НСВ: M(X) = (a + b)/2; Mo(X) [a, b]; Mе(X) = M[X] = (a+ b)/2; D(Х)=M[(X-m. X)2] = =M[X 2]-m. X 2 = =(b - a)2/12.

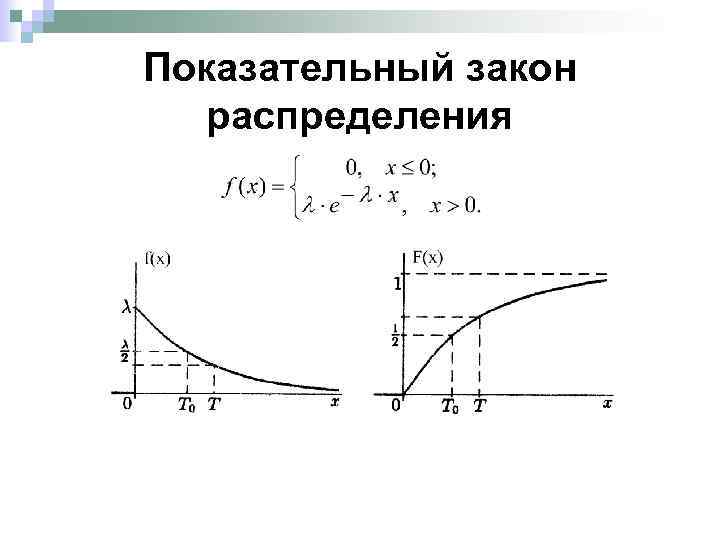Показательный закон распределения

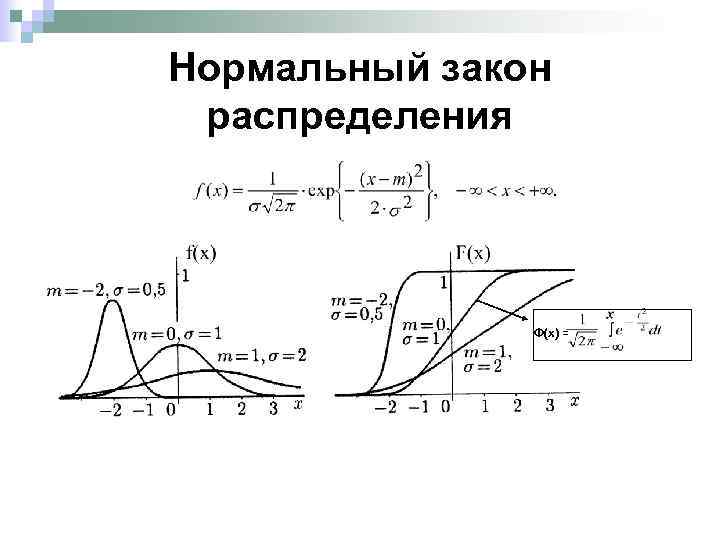Нормальный закон распределения Ф(х) =

РАЗДЕЛ X. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Тема 8. Предельные теоремы теории вероятностей

n n Первое неравенство Чебышева. Если СВ X 0 имеет конечное значение =M(X), то для любого 0 справедливо: P(X ) / или P(X < ) > 1 - /. Второе (основное) неравенство Чебышева. Если СВ X имеет конечные значения =M(X) и 2 = D(X), то для любого 0 справедливо: P( X - ) 2/ 2 или P( X - < ) > 1 - 2/ 2.

РАЗДЕЛ X. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Тема 9. Случайные процессы

n Опр. 1. Случайный процесс – это функция x(t, ), которая определяется так: фиксированном t x(t, ) является обычной случайной величиной (сечение случайного процесса в момент t). ¨ при фиксированном x(t, ) является обычной функцией (реализация случайного процесса). ¨ при

n n Опр. 2. Случайный процесс Х(t) называется марковским без последствия, если для любого момента t 0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t 0 и не зависит от того, когда и как система пришла в это состояние. Пусть Х(t) – марковский процесс и Sk – состояние процесса. Если t – дискретное, то X(t) – марковский процесс со счётным множеством значений и дискретным временем (дискретные цепи Маркова); если t – непрерывное, то X(t) – марковский процесс со счётным множеством значений и непрерывным временем.

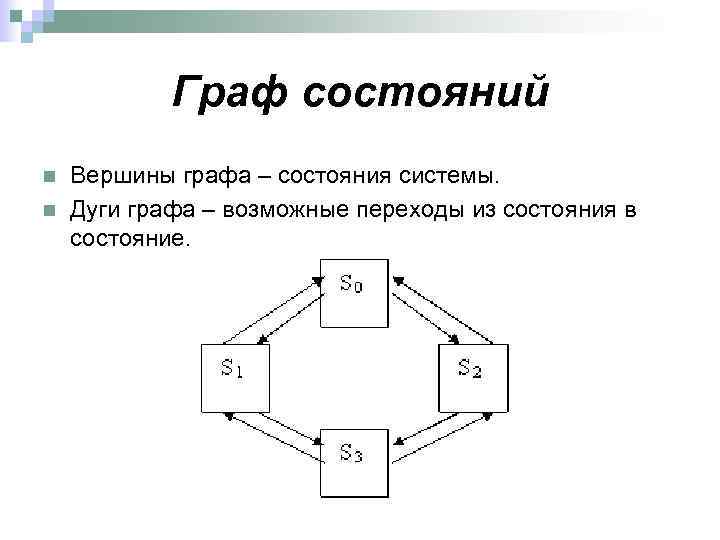Граф состояний n n Вершины графа – состояния системы. Дуги графа – возможные переходы из состояния в состояние.

n Опр. 3. X(t) – пуассоновский процесс, для которого вероятности состояний определяются так: P ( X(t) = k ) = n Пуассоновский процесс – это процесс, когда переход из состояния Si в состояние Sj возможен только в состояние Si+1 с интенсивностью . Остальные переходы маловероятны. Смысл : вероятность перехода из состояния Sj в состояние Si+1 будет равна t+o(t), где o(t) – бесконечно малая. Остальные вероятности перехода будут равны o(t). n

n Процесс размножения и гибели. Пусть X(t) – процесс, для которого переход из состояния Si возможен либо в состояние Si+1 (размножение), либо в состояние Si– 1 (гибель) (остальные переходы маловероятны); i – числовая характеристика, отвечающая за размножение (интенсивность размножения); i – числовая характеристика, отвечающая за гибель (интенсивность гибели).