Раздел VI ЛИНЕЙНЫЕ И ЕВКЛИДОВЫ ПРОСТРАНСТВА 1

Раздел VI. ЛИНЕЙНЫЕ И ЕВКЛИДОВЫ ПРОСТРАНСТВА § 1. ЛИНЕЙНЫЕ ПРОСТРАНСТВА

1. Определение линейного пространства. Примеры линейных пространств. 2. Свойства линейного пространства. 3. Линейная зависимость векторов. Свойства систем векторов. 4. Базис и ранг системы векторов. 5. Базис и размерность линейного пространства. Координаты вектора. 6. Преобразование координат вектора при переходе к другому базису. 7. Изоморфизм линейных пространств.

Вопрос 1. Определение линейного пространства. Примеры линейных пространств 1. 1. Определение линейного пространства Пусть L - непустое множество элементов любой природы и Р – поле (как правило, Р – поле действительных чисел R или поле комплексных чисел С).

О. 1. Множество L называется линейным или векторным пространством над полем Р, если выполнены три условия: 1. Задано сложение элементов L, т. е. закон, по которому любым элементам а, b L ставится в соответствие элемент s L, называемый суммой элементов а и b и обозначаемый s = а + b.

2. Задано умножение элемента на число, т. е. закон, по которому любому элементу а L и любому числу α Р ставится в соответствие элемент р L, называемый произведением элемента а на число α и обозначаемый р = αа. 3. Указанные законы (линейные операции) подчиняются аксиомам линейного пространства:

Аксиомы сложения 1. Для а, b L: а + b = b + a (коммутативность сложения). 2. Для а, b, с L: (a + b) + c = a + (b + c) (ассоциативность сложения). 3. Существует элемент θ L такой, что для а L: a + θ = a (элемент θ называется нулевым элементом). 4. Для а L существует элемент (–а) L такой, что a + (–а) = θ (элемент (–а) называется противоположным элементу a).

Аксиомы умножения 5. Для а L: 1· a = a. 6. Для а L и α, β Р: α(βa) = (αβ)a (ассоциативность относительно числового множителя).

Аксиомы, связывающие обе операции 7. Для а L и α, β Р: (α + β)a = αa + βa (дистрибутивность относительно суммы чисел). 8. Для а, b L и α Р: α(a + b) = αa +αb (дистрибутивность относительно суммы элементов).

Линейное пространство L над полем Р часто обозначается L(Р). Элементы линейного пространства называются векторами. О. 2. Линейное пространство над полем действительных чисел R (Р = R) называется действительным (вещественным) линейным пространством, а над полем комплексных чисел С (Р = С) – комплексным линейным пространством. Обозначения: L(R), L (С)

1. 2. Примеры линейных пространств Линейными пространствами над полем R являются: 1) множество V 3 (V 2) всех свободных векторов в пространстве (на плоскости); 2) множество D 3 (D 2) всех векторов в пространстве (на плоскости), выходящих из начала координат; 3) множество всех действительных функций;

4) множество С[а; b] всех действительных функций, непрерывных на отрезке [а; b]; 5) множество комплексных чисел С. Линейными пространствами над любым полем Р являются: 6) само поле Р; 7) множество Мm, n всех прямоугольных матриц размера m n с элементами из поля Р;

8) множество Р[х] всех многочленов над полем Р с обычными правилами сложения многочленов и умножения их на числа из поля Р; 9) множество Рn[х] всех многочленов степени не выше n с коэффициентами из поля Р.

1. 3. n-мерное арифметическое пространство О. 3. Множество упорядоченных наборов вида (х1, х2, …, хn), состоящих из n действительных чисел, в котором введены операции сложения (х1, х2, …, хn) + (у1, у2, …, уn) = = (х1 + у1, х2 + у2, …, хn + уn) и умножения на действительное число α(х1, х2, …, хn) = (αх1, αх2, …, αхn), называется n-мерным арифметическим действительным пространством и обозначается Rⁿ.

Элементы пространства Rⁿ называются nмерными арифметическими векторами и обозначаются х = (х1, х2, …, хn). В этом случае числа х1, х2, …, хn называются компонентами вектора х. В пространстве Rⁿ: θ = (0, 0, …, 0) – нулевой вектор; –х = (–х1, –х2, …, –хn) – противоположный вектору х.

Замечание 1. Элементы пространства Rⁿ можно рассматривать как векторы-строки длины n, так и как векторы-столбцы длины n:

2. Аналогично определяется n - мерное арифметическое комплексное пространство элементами которого являются упорядоченные наборы из n комплексных чисел. Операции в этом пространстве задаются по тем же правилам, что и в случае действительного арифметического пространства.

Вопрос 2. Свойства линейного пространства 1. Операцию сложения векторов можно распространить на любое конечное число векторов. 2. Любое линейное пространство L имеет только один нулевой вектор θ. 3. Каждый вектор линейного пространства имеет только один противоположный вектор.

4. Если вектор (–а) противоположен вектору а, то вектор а противоположен вектору (–а). 5. Для любых двух векторов а и b из L уравнение а + х = b относительно х всегда имеет решение и притом единственное. Поэтому в линейном пространстве L определена операция вычитания векторов b – а, обратная к операции сложения векторов. При этом b – а = b + (–а).

6. Произведение произвольного вектора а L на число 0 равно нулевому вектору, т. е. 0∙а = θ. 7. Произведение нулевого вектора θ на любое число α Р равно нулевому вектору, т. е. α·θ = θ. 8. Если α·а = θ, то либо α = 0, либо а = θ. 9. Вектор, противоположный данному вектору а, равен произведению а на число (– 1), т. е. (–а) = (– 1)·а.

10. Для а L и α Р выполняется равенство α(–a) = (–αa). 11. Для а, b L и α Р выполняется равенство α(a – b) = αa –αb. 12. Для а L и α, β Р выполняется равенство (α – β)a = αa – βa.

Вопрос 3. Линейная зависимость векторов. Свойства систем векторов О. 4. Вектор b называется пропорциональным вектору а, если b = λа для некоторого числа λ Р. О. 5. Системой векторов линейного пространства называется любая конечная последовательность элементов этого пространства.

О. 6. Подсистемами данной системы векторов называются сама эта система и любая система, получаемая из данной путем вычеркивания некоторых элементов. Пусть в линейном пространстве L(Р) задана конечная система векторов S = {а 1, а 2, …, аk}, (1) где аi L, i = 1, 2, …, k.

О. 7. Линейной комбинацией векторов системы (1) называется вектор а L , имеющий вид (2) где α 1, α 2, …, αk – произвольные числа из поля Р. При наличии равенства (2) говорят, что вектор а линейно выражается через векторы системы (1) или разлагается по этим векторам.

О. 8. Система векторов (1) называется линейно зависимой, если существуют такие числа α 1, α 2, …, αk Р, из которых хотя бы одно отлично от нуля, что линейная комбинация векторов (1) с указанными числами обращается в нулевой вектор пространства L, т. е. справедливо равенство (3)

О. 9. Если система векторов (1) такова, что равенство (3) возможно только при условии α 1 = α 2 = …= αk = 0, то эта система называется линейно независимой. Пример 1. Доказать, что система векторов е 1 =(1, 0, …, 0), е 2 =(0, 1, …, 0), …. , еn = (0, 0, …, 1) арифметического пространства Rⁿ является линейно независимой.

Решение Приравняем линейную комбинацию векторов е 1, е 2, …. , еn нулевому вектору θ = (0, 0, …, 0):

Вывод: система векторов {е 1, е 2, …. , еn } пространства Rⁿ является линейно независимой.

Т. 1. (критерий линейной зависимости векторов) Для того чтобы система векторов (1) при k > 1 была линейно зависимой, необходимо и достаточно, чтобы какойнибудь вектор этой системы линейно выражался через остальные векторы (т. е. являлся линейной комбинацией остальных векторов системы).

Т. 2. (свойства линейно зависимых систем векторов) 1. Система векторов, содержащая нулевой вектор, линейно зависима. 2. Система, состоящая из одного вектора а, линейно зависима тогда и только тогда, когда а = θ. 3. Система векторов, состоящая из двух пропорциональных векторов, линейно зависима. 4. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

Т. 3. (свойства линейно независимых систем векторов) 1. Все векторы линейно независимых систем являются ненулевыми. 2. Если система векторов линейно независима, то и любая ее подсистема тоже линейно независима. 3. Если система векторов (1) линейно независима и вектор b L не является линейной комбинацией векторов системы (1), то расширенная система векторов {а 1, а 2, …, аk, b} является линейно независимой.

Вопрос 4. Базис и ранг системы векторов О. 10. Две системы векторов называются эквивалентными, если любой вектор каждой из этих систем линейно выражается через векторы другой системы.

Пример 2. Системы S 1 = {а, b} и S 2 = {2 а + b, а + b} эквивалентны, так каждый вектор системы S 2 линейно выражается через векторы системы S 1. Векторы системы S 1 так же линейно выражается через векторы системы S 2: а =(2 а + b) – (а + b), b =2(а + b) – (2 а + b). Т. 4. Любые две эквивалентные линейно независимые системы векторов имеют одинаковое число векторов.

Пусть дана конечная система векторов (1): S = {а 1, а 2, …, аk}. О. 11. Базисом (базой) системы векторов (1) называется любая ее конечная подсистема, удовлетворяющая следующим условиям: 1) векторы этой подсистемы линейно независимы; 2) каждый вектор системы (1) может быть линейно выражен через векторы данной подсистемы.

О. 12. Линейно независимая подсистема векторов, добавление к которой любого вектора системы (1) делает ее линейно зависимой, называется максимальной линейно независимой подсистемой данной системы векторов (1). О. 13. Базисом системы векторов (1) называется максимальная линейно независимая подсистема данной системы векторов.

О. 14. Число векторов в базисе данной системы векторов (1) называется рангом системы векторов (1). Обозначение: rang S, r(S). Замечание Система векторов может иметь несколько различных базисов, однако любые два базиса эквивалентны между собой и содержат одинаковое число векторов ранг системы векторов определяется однозначно.

О. 15. Следующие преобразования системы векторов называются элементарными: 1) умножение произвольного вектора системы на любое число, отличное от нуля; 2) прибавление к некоторому вектору системы любого другого вектора, умноженного на число; 3) перемена местами двух векторов; 4) удаление нулевого вектора.

Т. 5. Ранг системы векторов сохраняется при элементарных преобразованиях системы. Замечание Для того чтобы вычислить ранг системы векторов (1) в n-мерном арифметическом пространстве Rⁿ следует из этих векторов как строк записать матрицу и вычислить ее ранг.

Пример 3. Найти ранг системы векторов а 1 =(1, -1, 2, 1), а 2 =(1, -1, 1, 2), а 3 =(1, -1, 4, -1) и выделить в ней все базисы. Решение

Базисы: {а 1, а 2}, {а 1, а 3}, {а 2, а 1}, {а 3, а 2}.

Вопрос 5. Базис и размерность линейного пространства. Координаты вектора О. 16. Базисом (базой) линейного пространства L называется любая конечная упорядоченная система векторов В = {е 1, е 2, …, еn} из этого пространства, удовлетворяющая условиям: 1) векторы этой системы линейно независимы; 2)каждый вектор пространства L может быть линейно выражен через векторы данной системы.

Если В = {е 1, е 2, …, еn} – базис пространства L, то любой вектор а L может быть записан в виде (4) где 1, 2, …. , n Р. Выражение (4) называется разложением вектора а по базису В.

Т. 6. (о единственности разложения) В линейном пространстве L над полем Р разложение любого вектора а L по данному базису единственно. О. 17. Коэффициенты разложения вектора а по базису В в равенстве (4), т. е. числа 1, 2, …. , n, называются координатами вектора а в базисе В. Обозначение: а = ( 1, 2, …. , n)В.

Т. 7. (о линейных операциях в координатной форме) При сложении любых двух векторов в линейном пространстве их координаты в одном и том же базисе складываются, а при умножении вектора на число его координаты умножаются на это число. Если а = ( 1, 2, …. , n)В и b = (β 1, β 2, …. , βn)В, то а + b = ( 1 + β 1, 2 + β 2, …. , n + βn)В, λа = (λ 1, λ 2, …. , λ n)В, где λ Р.

5. 2. Примеры базисов 1. Любая упорядоченная тройка некомпланарных векторов образует базис пространства V 3 (множество векторов в пространстве). Частный случай – декартов прямоугольный базис

2. В n-мерном арифметическом пространстве Rⁿ векторы е 1 =(1, 0, …, 0), е 2 =(0, 1, …, 0), …. , еn =(0, 0, …, 1) образуют базис В = {е 1, е 2, …, еn}, который называется стандартным или естественным базисом арифметического пространства Rⁿ. В стандартном базисе В любой n-мерный вектор х = (х1, х2, …, хn) Rⁿ представим в виде т. е. компоненты n-мерного вектора х совпадают с его координатами в стандартном базисе.

3. В пространстве Р[х] всех многочленов над полем Р примером базиса является система многочленов: 1, х, х², х³, …. 4. В пространстве Рn[х] всех многочленов степени не выше n с коэффициентами из поля Р примером базиса является система многочленов: 1, х, х², …. , хⁿ. В пространстве Рn[х] в качестве базиса можно так же взять систему многочленов: 1, х – , (х – )², …. , (х – )ⁿ, где 0 – некоторое фиксированное число из поля Р.

5. 3. Размерность линейного пространства О. 18. Максимальное количество линейно независимых векторов в данном линейном пространстве называется размерностью линейного пространства.

О. 19. Если размерность линейного пространства L равна n, т. е. существует линейно независимая система из n векторов, а любая система векторов, содержащая n + 1 вектор или более, линейно зависима, то линейное пространство L называется n-мерным или конечномерным. Размерность такого линейного пространства обозначают так: dim L=n (от англ. dimension) или Ln.

О. 20. Если в линейном пространстве L существует любое (сколь угодно большое) число линейно независимых векторов, то пространство L называется бесконечномерным. Обозначение: dim L = ∞.

Пример 4. 1. Размерность пространства, состоящего из одного нулевого вектора θ, равна 0. 2. Линейное пространство функций С[0; 1], непрерывных на отрезке [0; 1], является бесконечномерным, так как для любого n N система многочленов 1, х, х², …. , хⁿ, являющихся элементами этого пространства, линейно независима.

Т. 8. Если L – n-мерное линейное пространство (dim L = n), то любые n линейно независимых векторов этого пространства образуют его базис. Т. 9. Если в линейном пространстве L существует базис из n векторов, то dim L = n. Из т. 8 и т. 9 в каждом линейном пространстве L любые два базиса содержат одно и тоже количество векторов, и это количество векторов равно размерности линейного пространства.

О. 21. Размерностью конечномерного линейного пространства L называется число векторов его базиса. Пример 5. 1. В арифметическом пространстве Rⁿ стандартный базис состоит из n векторов, поэтому dim Rⁿ = n. 2. dim V 2 = 2, dim V 3 = 3, dim Рn[х] = n + 1.

Вопрос 6. Преобразование координат вектора при переходе к другому базису Пусть в n-мерном линейном пространстве L заданы два базиса: и Выразим векторы нового базиса В' через векторы старого базиса В, т. е. разложим векторы по векторам е 1, е 2, …, еn:

т. е.

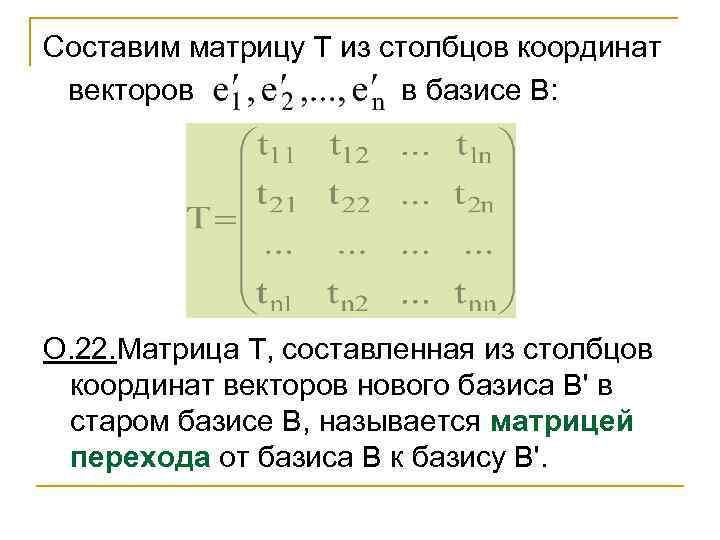Составим матрицу Т из столбцов координат векторов в базисе В: О. 22. Матрица Т, составленная из столбцов координат векторов нового базиса В' в старом базисе В, называется матрицей перехода от базиса В к базису В'.

Свойства матрицы перехода 1. Матрица перехода Т невырожденная (|Т| 0) и всегда имеет обратную матрицу. 2. Если в n-мерном пространстве L задан базис В, то для любой невырожденной квадратной матрицы Т n-го порядка существует такой базис В' в этом линейном пространстве, что Т будет матрицей перехода от базиса В к базису В'.

3. Если Т – матрица перехода от старого базиса В к новому базису В' линейного пространства, то - матрица перехода от базиса В' к базису В. 4. Если в линейном пространстве заданы базисы В, В' и В'', причем Т 1 - матрица перехода от базиса В к базису В', а Т 2 матрица перехода от базиса В' к базису В'', то произведение этих матриц Т 1·Т 2 матрица перехода от базиса В к базису В''.

Пусть х – произвольный вектор линейного пространства L, причем х = (х1, х2, …, хn)В и Запишем координаты вектора х в виде матриц:

Связь между координатами вектора х в базисах В и В' (5)

(6) Соотношения (5) и (6) называются формулами преобразования координат вектора при изменении базиса пространства.

Вопрос 7. Изоморфизм линейных пространств Пусть L и L' – линейные пространства над одним и тем же полем Р. О. 23. Два линейных пространства L и L' называются изоморфными, если существует биективное отображение φ: L→L', удовлетворяющее условиям: 1) φ(а + b) = φ(а) + φ(b) для любых а, b L; 2) φ(λа) = λφ(а) для любых а L, λ Р.

При этом отображение φ называется изоморфизмом линейных пространств L и L'. Обозначение: L ≅ L'.

Пример 6. 1. Линейное пространство V 2 геометрических векторов на плоскости с обычными операциями сложения векторов и умножения их на действительные числа изоморфно действительному арифметическому пространству R²: вектор ā его координаты (а 1, а 2).

2. Линейное пространство Р 2[х] всех многочленов степени n 2 с действительными коэффициентами с обычными операциями сложения многочленов и умножения их на действительные числа изоморфно действительному арифметическому пространству R³: f(х) = а 0 + а 1 х + а 2 х² (а 0, а 1, а 2).

Т. 10. Два конечномерных линейных пространства изоморфны тогда и только тогда, когда они имеют одинаковую размерность. Следствие Все n-мерные линейные пространства над полем R (С) изоморфны n-мерному арифметическому пространству Rⁿ (Сⁿ).