Раздел N 4 Дифференциальные уравнения Лекция N 5

Раздел N 4 Дифференциальные уравнения. Лекция N 5 Дифференциальные уравнения первого и второго порядка.

Задача о скорости размножения бактерий Известно, что скорость размножения бактерий пропорциональна их количеству. В начальный момент имеется 100 бактерий, в течение 3 часов их количество удвоилось. Требуется найти зависимость количества бактерий от времени. Решение. Пусть число бактерий в произвольный момент времени х. Поскольку скорость размножения бактерий - это прозводная, то можно записать так: k – коэффициент пропорциональности Получено уравнение записанное в виде : Получили уравнение, в котором присутствует первая производная функции

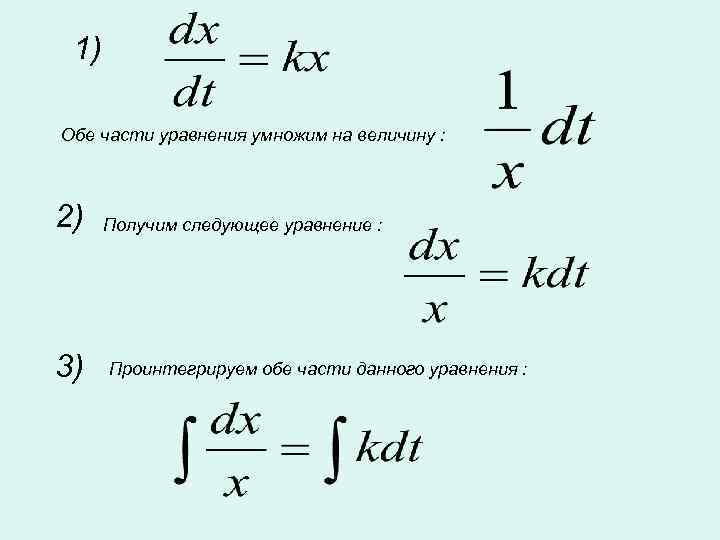1) Обе части уравнения умножим на величину : 2) 3) Получим следующее уравнение : Проинтегрируем обе части данного уравнения :

4) 5) 6) По условию задачи известно, что x (t =0) = 100

Задача о радиоактивном распаде Скорость распада радия (Ra) в каждый момент времени пропорциональна его наличной массе. Найти закон радиоактивного распада, если известно, что в начальный момент имелось N 0 атомов. Решение: Будем считать, что за малый промежуток времени dt распадается число ядер d. N. Очевидно, что это число пропорционально промежутку времени dt и общему числу нераспавшихся к данному моменту радиоактивных ядер N. Число нераспавшихся ядер убывает со временем по экспоненте !

В общем виде подобные уравнения можно записать в виде : или Определение. Уравнение, связывающее независимую переменную, функцию и ее производные называют дифференциальным.

Определение. Если в уравнении функция зависит от одной переменной, то дифференциальное уравнение называют обыкновенным. Общий вид обыкновенного дифференциального уравнения имеет вид: или Определение. Порядком дифференциального уравненя порядок старшей производной, входящей в него. называется

Обыкновенные дифференциальные уравнения первого порядка Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида: где x - независимая переменная, y(x) - неизвестная функция Общим решением дифференциального ур-я будет множество решений: C – произвольная постоянная Общее решение: Пример: общее решение:

Функция y(x) называется решением (или интегралом) дифференциального уравнения если при подстановке ее в уравнение обращает его в тождество.

Разделяют несколько типов (видов) обыкновенных дифференциальных уравнений: -Уравнения с разделяющимися переменными, -Однородные уравнения, -Линейные уравнения, - Уравнения второго порядка -и т. д. Остановимся подробнее на каждом из этих типов уравнений.

Уравнения с разделенными переменными. Так называются уравнения вида удовлетворяющее начальному условию: f (x)dx + g (y)dy = 0 Интегрируя, получим - общий интеграл (общее решение) этого уравнения. Пример: - общее решение

Уравнения с разделяющимися переменными. Так называются уравнения вида: Эти уравнения легко сводятся к уравнению с разделёнными переменными: Записываем уравнение в форме: затем делим на g(y) и умножаем на dx: . Это уравнение - с разделёнными переменными. Интегрируя, получим общий интеграл:

Пример: Выразим у из последнего выражения как функцию х, получим общее решение:

Однородные дифференциальные уравнения первого порядка. Так называются уравнения со специальным видом зависимости функции f(x, y) от своих аргументов: Это уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции u(x) заменой: Подставляя в уравнение y = x·u, y ′ = u + x·u ′, получим (это - уравнение с разделяющимися переменными), - это общий интеграл уравнения относительно переменных x, u

В общем случае однородные дифференциальные уравнения можно представить в виде : Где , P(x; y), Q(x; y) – однородные функции измерения m, т. е

Пример: Решение: 1) Положим y = ux 2) 3) 4) 5) Разделим на x 2 , x≠ 0

Разделяя переменные и перенося за знак равенства, получим: 6) 7) 8) 9) 10)

11) 12) Возвращаясь к прежней неизвестной переменной y получим окончательный ответ:

Линейные дифференциальные уравнения первого порядка. ДУ первого порядка называется линейным, если неизвестная функция y(x) и её производная входят в уравнение в первой степени: Примеры: здесь p(x), q(x) - непрерывные функции.

Решение линейных ДУ методом И. Бернулли Для решения уравнения представим y(x) в виде произведения двух новых неизвестных функций u(x) и v(x): y(x) = u(x)v(x). Тогда 1) и уравнение приводится к виду: 2) или: 3) Это уравнение решаем в два этапа: сначала находим функцию v(x) как частное решение уравнения с разделяющимися переменными (v можно выбрать произвольно, тогда): За v можно выбрать любое частное решение затем находим u(x) из уравнения: 4)

5) 6) Отметим, решая уравнение на v(x) мы не вводим в это решение произвольную постоянную C, нам достаточно найти одну функцию v(x), обнуляющую слагаемое со скобками. Запоминать эту формулу не надо, лучше усвоить порядок действий и воспроизводить его при решении каждой задачи.

Пример: Решение: и общее решение уравнения

Для нахождения частного решения, соответствующего начальным условиям (задача Коши), подставим в общее решение Решение задачи:

Обыкновенные дифференциальные уравнения второго порядка Дифференциальным уравнением второго порядка называется уравнение вида: или

Дифференциальные уравнения второго порядка, допускающие понижение порядка. Общее решение дифференциального уравнения можно найти путём двукратного интегрирования, последовательно понижая порядок на единицу: - Общее решение уравнения

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. p, q – постоянные действительные числа Для того чтобы найти общее решение данного уравнения, необходимо знать два частных решения y 1(x) и y 2(x) Тогда общее решение исходного уравнения можно найти так : Будем искать решения в виде: Подставляя в исходное уравнение, получим: y = ekx где k предстоит определить

Так как, то: Полученное уравнение называют характеристическим, корни данного уравнения будут определять решение исходного уравнения второго порядка.

1. Корни характеристического уравнения являются действительными и различными: 2. Корни характеристического уравнения являются действительными и равными: 3. Корни характеристического уравнения являются комплексными и сопряженными:

Примеры применения дифференциальных уравнений 1 Модель химической реакции x, y, b – концентрации химических компонентов k 0 = k 0 / A k 1 k 2 - константы скоростей компонентов

1) 2)

2 Экологическая модель Вольтерра X - концентрация зайцев y - волков ε 1 ε 2 - константы скоростей размножения зайцев и волков γ 1 γ 2 - константы скоростей смертности зайцев и волков