РАЗДЕЛ 9 ИСТЕЧЕНИЕ ГАЗОВ И ПАРОВ 1 ПЕРВЫЙ

РАЗДЕЛ 9. ИСТЕЧЕНИЕ ГАЗОВ И ПАРОВ 1. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ В ПРИМЕНЕНИИ К ПОТОКУ ДВИЖУЩЕГОСЯ ГАЗА

В процессах изменения состояния движущегося с конечной скоростью газа теплота расходуется не только на изменение внутренней энергии и на совершение внешней работы (против внешних сил), но и на приращение внешней кинетической энергии газа при его перемещении по каналу (паровые турбины, газовые турбины, реактивные двигатели, ракеты и др. ) (9. 1)

Изменение кинетической энергии рабочего тела может происходить как в трубах постоянного сечения, так и в специальных каналах переменного сечения, называемых соплами и диффузорами. Если при перемещении газа по каналу происходит его расширение с уменьшением давления и увеличением скорости, то такой канал называется соплом. Если в канале происходит сжатие рабочего тела с увеличением давления и уменьшением скорости, то такой канал называется диффузором.

2. РАБОТА ПРОТАЛКИВАНИЯ. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ УРАВНЕНИЯ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ ДЛЯ ПОТОКА - Удельная работа проталкивания (работа против внешних сил) Условия истечения газа: 1. Осуществляется условие неразрывности струи, т. е. через любое поперечное сечение канала в единицу времени протекает одинаковая масса рабочего тела: (а)

2. Течение газа по каналу осуществляется без подвода и отвода теплоты, т. е. адиабатно. 3. В каждом поперечном сечении канала скорость w, давление р, температура Т и другие параметры рабочего тела постоянны по сечению, т. е. имеют во всех точках плоскости, перпендикулярной оси трубы, одинаковое значение (осредненные величины). 4. Рассматривается установившееся движение, называемое стационарным. При этом величины v, w, p, T могут меняться по длине канала, но в каждом сечении, к которому они относятся, не зависят от времени. Все величины являются только функцией координат.

Предположим, что по каналу переменного сечения перемещается газ Элементарная работа проталкивания газа на бесконечно малом пути между сечениями I—I и II—II за 1 с: (б)

Из (а) следует, что или Элементарная работа проталкивания: (9. 2) или (9. 3)

Уравнение (9. 3) показывает, что подведенное количество теплоты в процессе при течении газа (или жидкости) расходуется на: -изменение внутренней энергии; -на работу проталкивания; -на изменение внешней кинетической энергии рабочего тела. Или подведенное количество теплоты при течении газа расходуется на: - изменение его энтальпии; - внешней кинетической энергии.

Когда движущийся газ совершает полезную работу lтех (техническую) над внешним объектом и в нем изменяется потенциальная энергия положения (H — H 1 — пьезометрическая высота), то закон сохранения энергии приводит к следующему уравнению: (9. 4) Полученное уравнение справедливо как для обратимых, так и для необратимых (происходящих с трением) процессов.

В случае отсутствия теплообмена между текущим рабочим телом и окружающей средой (адиабатное течение) при H = H 1 и lтех = 0, что встречается наиболее часто, уравнение (9. 4) принимает вид: или (9. 5) Изменение внешней кинетической энергии рабочего тела происходит за счет уменьшения его удельной энтальпии.

Когда начальная скорость рабочего тела равна нулю, тогда скорость течения определяется формулой: Если энтальпия выражается в килоджоулях на килограмм, то последнее уравнение принимает вид: (9. 6) Значения удельной энтальпии h 1 и h 2 определяются по hs-диаграмме или по таблицам для данного вещества.

3. РАСПОЛАГАЕМАЯ РАБОТА ПРИ ИСТЕЧЕНИИ ГАЗА • Величина dw 2/2, равная бесконечно малому приращению внешней кинетической энергии рабочего тела, называется элементарной располагаемой работой. • Эта энергия может быть использована для получения внешней полезной работы.

Из сравнения уравнений (5. 13) и (9. 3) следует, что для обратимого процесса течения газа или (9. 7) Если dp > 0, то газ сжимается и его скорость уменьшается: dw < 0. Если dp < 0, то газ расширяется и его скорость увеличивается: dw > 0.

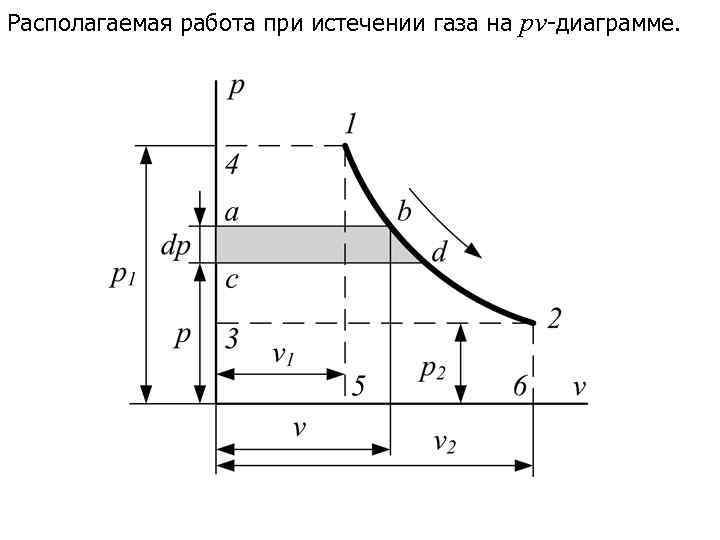Располагаемая работа при истечении газа на pv-диаграмме.

(9. 8) (9. 9) (9. 10)

Сравнивая располагаемую работу при истечении (пл. 1234) с работой расширения газа (пл. 1265), получаем, что располагаемая работа в n раз больше работы расширения газа: Из уравнения (9. 3) следует, что или Располагаемая работа при течении газа может быть получена за счет внешней теплоты и уменьшения энтальпии газа. Это уравнение справедливо как для обратимых, так и для необратимых процессов течения газа с трением.

При адиабатном течении из уравнения (9. 5): (9. 11) При необратимом истечении газа располагаемая работа при том же перепаде давления меньше, так как энтальпия в конечном состоянии будет больше за счет полученной теплоты трения. Практически расчет ведется обычно для идеального (обратимого) процесса течения, а необратимость процесса учитывается эмпирическим коэффициентом, который всегда меньше единицы.

4. АДИАБАТНЫЙ ПРОЦЕСС ИСТЕЧЕНИЯ ГАЗА Скорость истечения газа при адиабатном процессе определяется из основного уравнения располагаемой работы: или (9. 12)

5. ИСТЕЧЕНИЕ КАПЕЛЬНОЙ ЖИДКОСТИ Скорость истечения жидкости определяется уравнением (9. 12). Располагаемая работа несжимаемой жидкости (при v = const): (9. 13)

Графически располагаемая работа при истечении капельной жидкости изображается пл. abcd

6. СКОРОСТЬ ИСТЕЧЕНИЯ И МАССОВЫЙ РАСХОД ИДЕАЛЬНОГО ГАЗА ИЗ СУЖИВАЮЩЕГОСЯ СОПЛА (9. 14) Скорость истечения газа зависит от состояния газа при входе в сопло и от давления р2 на выходе

Массовый расход газа в килограммах в секунду при истечении: (9. 15) При адиабатном истечении идеального газа: С учетом вышесказанного массовый расход идеального газа: (9. 16) Массовый расход идеального газа зависит от площади выходного сечения канала, начального состояния газа и степени его расширения.

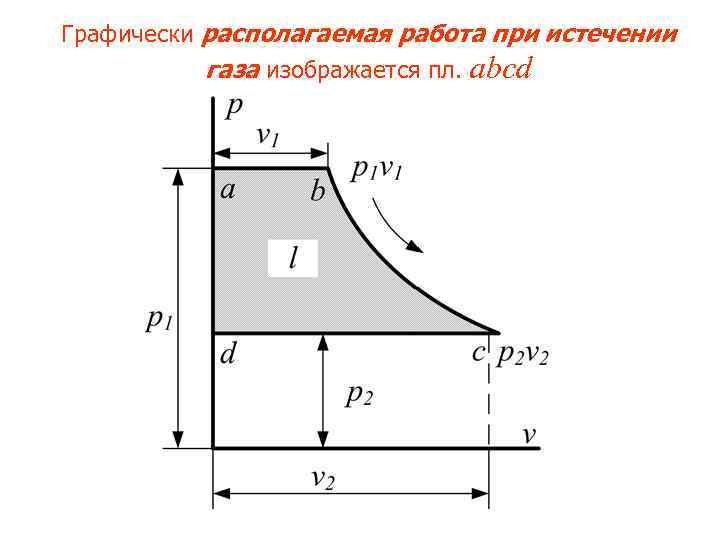Графически располагаемая работа при истечении газа изображается пл. abсd

7. АНАЛИЗ УРАВНЕНИЯ МАССОВОГО РАСХОДА ИДЕАЛЬНОГО ГАЗА И КРИТИЧЕСКОЕ ДАВЛЕНИЕ

Для объяснения противоречия между выводами анализа и опытными данными ученые Сен-Венан и Вантцель предложили следующую гипотезу: Для значений давление в устье суживающегося канала равно давлению среды, куда происходит истечение, поэтому теория совпадает с опытными данными. Для значений давление в устье суживающегося канала перестает быть равным давлению среды и, даже, несмотря на понижение давления среды до Величина βк зависит только от полного вакуума, остается постоянным. показателя адиабаты k, т. е, зависит от природы рабочего (9. 17) тела

Для одноатомного газа k=1, 66 и βк = 0, 49; для двухатомного газа k=1, 4 и βк = 0, 528; для трехатомного газа k=1, 3 и βк = 0, 546. Давление в выходном сечении сопла при достижении максимального расхода, называется критическим давлением (9. 18) Критическое давление равно начальному давлению, умноженному на коэффициент βк. При заданном начальном давлении критическое давление — наименьшее давление, которое устанавливается в выходном сечении суживающегося сопла.

8. КРИТИЧЕСКАЯ СКОРОСТЬ И МАКСИМАЛЬНЫЙ РАСХОД ИДЕАЛЬНОГО ГАЗА (9. 19) Критическая скорость при истечении идеального газа зависит только от начальных параметров и его природы.

Критическая скорость равна скорости звука в газе при параметрах ркр и vкр : (9. 20)

При критическом давлении в выходном сечении канала устанавливается максимальный расход газа, который определяем из уравнения (9. 16) при замене p 2/p 1 на значение его из уравнения (9. 17). После соответствующих преобразований получаем: (9. 21) Максимальный расход газа вполне определяется начальным состоянием газа, площадью выходного сечения амин и природой газа, т. е. показателем адиабаты k.

9. ОСНОВНЫЕ УСЛОВИЯ ТЕЧЕНИЯ ИДЕАЛЬНОГО ГАЗА ПО КАНАЛАМ ПЕРЕМЕННОГО СЕЧЕНИЯ (а) (б) (9. 22) Уравнение (9. 22) определяет условия неразрывности струи и показывает, что форма канала зависит от изменения объема газа и его скорости. Доказательство на СРС В зависимости от скорости газа при входе один и тот же канал может быть и соплом и диффузором.

10. РЕЖИМЫ ИСТЕЧЕНИЯ ИДЕАЛЬНОГО ГАЗА ИЗ СУЖИВАЮЩЕГОСЯ СОПЛА Первый режим. Давление внешней среды больше критического, или когда При этих условиях: 1) используется весь перепад давления от р1 до р2 (рис. 9. 7) и происходит полное расширение газа; 2) скорость газа в выходном сечении сопла меньше скорости звука (рис. 9. 8) (w 2 < c) – дозвуковой режим; 3) давление газа в выходном сечении сопла равно давлению внешней среды; 4) скорость истечения и массовый расход газа при заданном выходном сечении определяются по формулам (9. 14) и (9. 16). w 2 < wкр, m < mmax

lpacn графически представится пл. 1234 Рис. 9. 7 Рис. 9. 8 Площадь выходного сечения сопла а можно определить из формулы (9. 16) (при заданном расходе): (9. 23)

Второй режим. Давление внешней среды равно критическому, или когда 1. На срезе сопла устанавливается критическое давление pкр; 2. Происходит полное расширение от р1 до ркр; 3. Вся располагаемая работа lрасп расходуется на приращение кинетической энергии потока; 4. В выходном сечении сопла устанавливается критические параметры ркр и wкр; 5. Расход через сопло будет максимальным mmax.

Третий режим. Давление внешней среды меньше критического, или При этих условиях: 1) используется не весь перепад давлений от р1 до р2, а только часть от р1 до ркр (рис. 9. 9); 2) происходит неполное расширение газа, и скорость газа в выходном сечении суживающегося сопла равна критической скорости или местной скорости звука (рис. 9. 10) (расширение от ркр до р2 будет происходить уже вне сопла и поэтому не даст дополнительного увелчения скорости); 3) давление в устье сопла равно критическому давлению: Используется только часть lрасп на увеличение кинетической энергии потока и имеет место потеря энергии бесполезно рассеиваемой в пространстве за соплом. 4) критическая скорость истечения и максимальный расход идеального газа определяются по формулам (9. 19) и (9. 21).

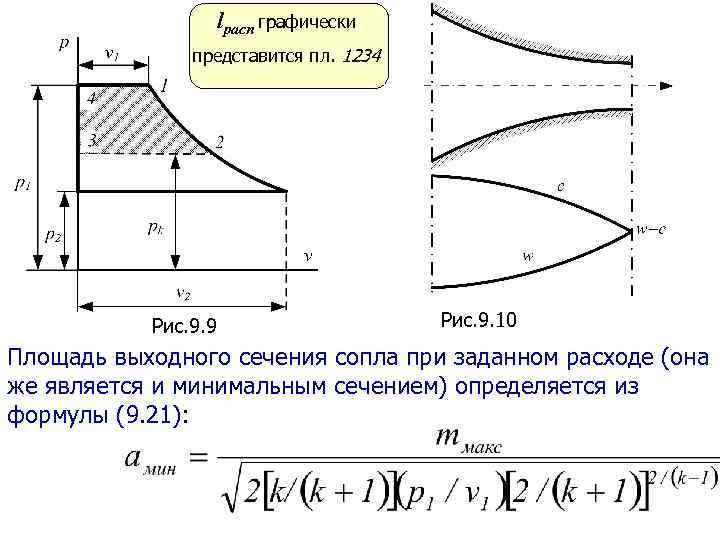lpacn графически представится пл. 1234 Рис. 9. 9 Рис. 9. 10 Площадь выходного сечения сопла при заданном расходе (она же является и минимальным сечением) определяется из формулы (9. 21):

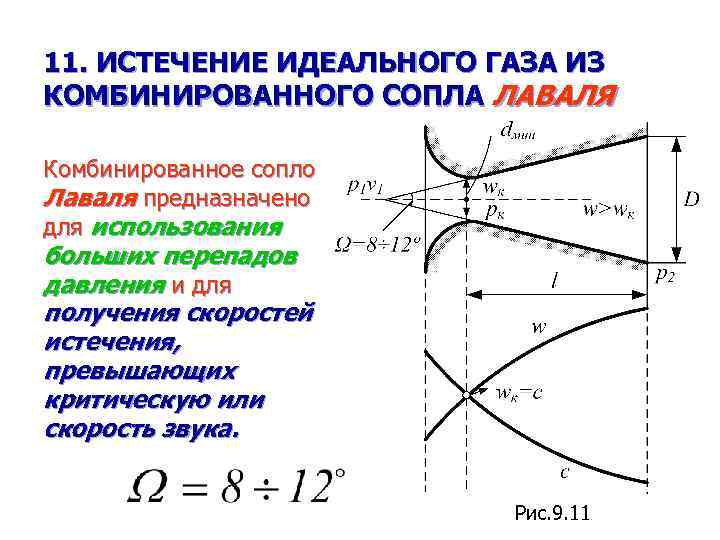11. ИСТЕЧЕНИЕ ИДЕАЛЬНОГО ГАЗА ИЗ КОМБИНИРОВАННОГО СОПЛА ЛАВАЛЯ Комбинированное сопло Лаваля предназначено для использования больших перепадов давления и для получения скоростей истечения, превышающих критическую или скорость звука. Рис. 9. 11

• При истечении газа из комбинированного сопла в • • • окружающую среду с давлением меньше критического в самом узком сечении сопла устанавливаются критическое давление ркр и критическая скорость wкр. В расширяющейся насадке сопла происходит дальнейшее увеличение скорости газа и падение давления до давления внешней среды. Скорость истечения и массовый расход идеального газа (при заданном а) определяются по формулам (9. 14) и (9. 16). При заданном расходе площадь минимального сечения сопла амин можно вычислить по формуле (9. 21), а площадь выходного сечения сопла а — по формуле (9. 16). Длина суживающейся части обычно берется равной диаметру выходного критического сечения сопла или из конструктивных соображений. Длину расширяющейся насадки l (рис. 9. 11) можно определить по уравнению

12. ИСТЕЧЕНИЕ ГАЗОВ С УЧЕТОМ ТРЕНИЯ С учетом сил трения скорость газа при том же Δр в любом канале будет меньше скорости обратимого процесса (теоретической скорости). Отношение действительной скорости газа wд к теоретической w называют коэффициентом скорости (или скоростным коэффициентом): или (9. 24) - коэффициент потери энергии - коэффициент полезного действия канала (9. 25)

Теплота трения без учета начальной скорости: где h 1, h 2 — энтальпия рабочего тела в начале и конце обратимого адиабатного (изоэнтропного) процесса расширения. Уравнения (9. 24) и (9. 25) справедливы как для идеального, так и реального газов.

13. ИСТЕЧЕНИЕ ВОДЯНОГО ПАРА Для водяного пара все формулы и закономерности теории истечения можно применять только для приближенных вычислений, если считать для перегретого пара значение k = 1, 3, а для сухого насыщенного пара k = 1, 135. (9. 6) Массовый расход определяется из уравнения неразрывности для критического режима истечения При необратимом процессе истечения .

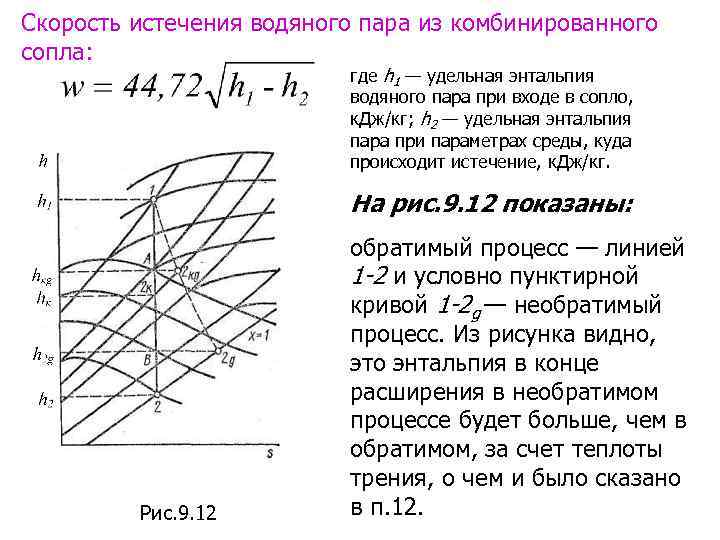Скорость истечения водяного пара из комбинированного сопла: где h 1 — удельная энтальпия водяного пара при входе в сопло, к. Дж/кг; h 2 — удельная энтальпия пара при параметрах среды, куда происходит истечение, к. Дж/кг. На рис. 9. 12 показаны: Рис. 9. 12 обратимый процесс — линией 1 -2 и условно пунктирной кривой 1 -2 g — необратимый процесс. Из рисунка видно, это энтальпия в конце расширения в необратимом процессе будет больше, чем в обратимом, за счет теплоты трения, о чем и было сказано в п. 12.