Раздел 7 Квантовая механика и атомная физика Тема

Раздел 7 Квантовая механика и атомная физика Тема 1. Волновые свойства вещества

Гипотеза де Бройля (1924) 1. Дуализм (корпускулярные и волновые свойства) не является только оптическим явлением. Все частицы обладают этим свойством. 2. Движение любой частицы является волновым процессом с длиной волны l. формула де Бройля p - импульс частицы

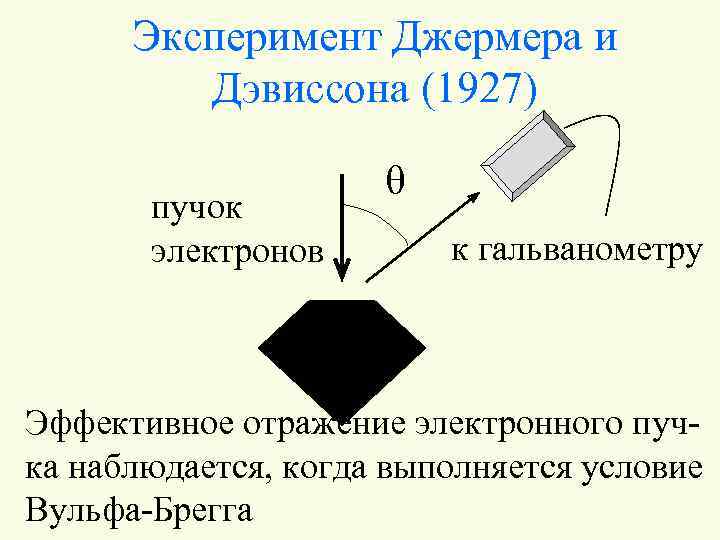Эксперимент Джермера и Дэвиссона (1927) пучок электронов q к гальванометру Эффективное отражение электронного пучка наблюдается, когда выполняется условие Вульфа-Брегга

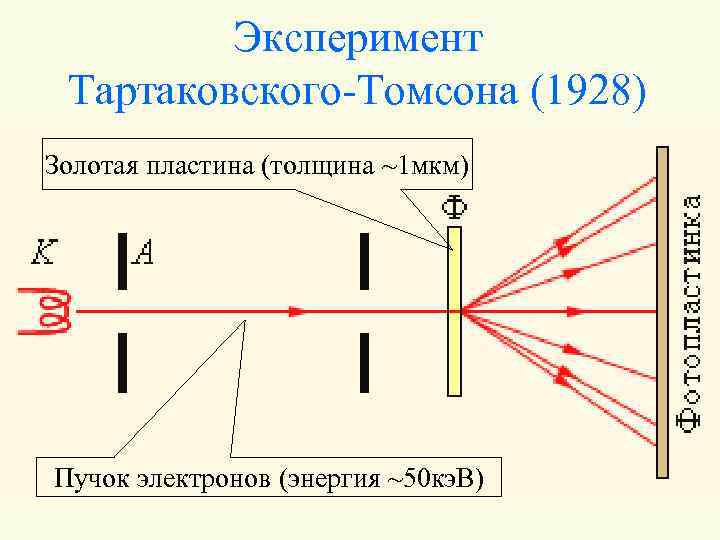Эксперимент Тартаковского-Томсона (1928) Золотая пластина (толщина ~1 мкм) Пучок электронов (энергия ~50 кэ. В)

Изображение на фотопластинке

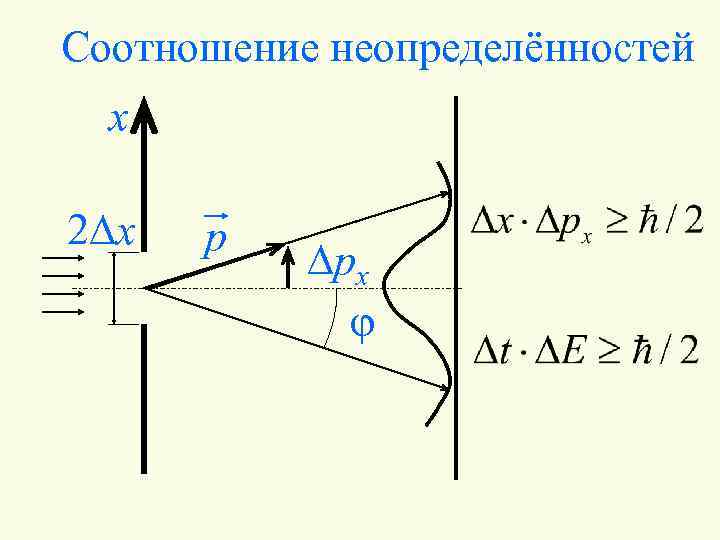Соотношение неопределённостей x 2 Dx p Dpx j

Постулаты квантовой механики 1. Состояние частицы описывается волновой функцией (Y-функцией), которая обладает следующими свойствами: • непрерывная; • гладкая (непрерывно дифференцируемая); • ограниченная; • нормированная.

Вероятностный смысл волновой функции |Y(x, y, z)|2 -плотность вероятности обнаружения частицы в точке с координатами (x, y, z). Вероятность обнаружения частицы в объёме dxdydz в точке (x, y, z) равна 2 dxdydz. |Y(x, y, z)|

2. Принцип суперпозиции Если частица может находиться в состояниях Y 1 и Y 2, то она может находиться и в состоянии Y=C 1 Y 1+C 2 Y 2, где C 1, С 2 - комплексные числа. 3. Квантовые операторы Любой физической величине соответствует линейный эрмитовый оператор.

Волна де Бройля и операторы физических величин -волновая функция свободной частицы с импульсом p и энергией E. - оператор импульса - оператор энергии

4. Уравнение Шредингера потенциальная энергия частицы оператор энергии гамильтониан частицы

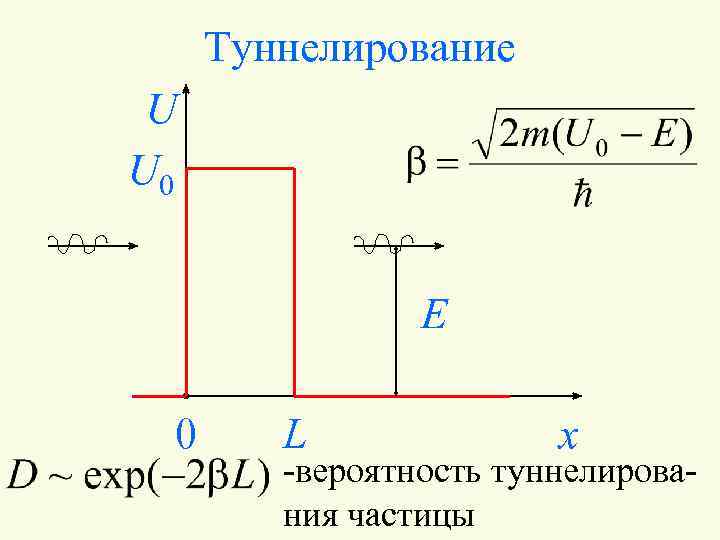Туннелирование U U 0 E 0 L x -вероятность туннелирования частицы

Стационарное уравнение Шредингера E - средняя энергия частицы, находящейся в стационарном состоянии Y; U( r ) -потенциальная энергия частицы.

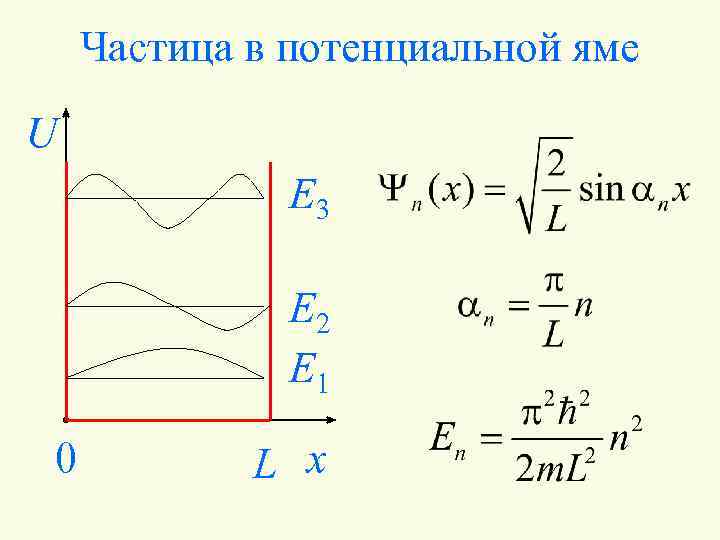Частица в потенциальной яме U E 3 E 2 E 1 0 L x