Развертка пирамиды_призмы.ppt
- Количество слайдов: 31
 Раздел 6. Развертка поверхностей Под разверткой поверхности понимают гибкую нерастяжимую оболочку (пленку), которая, будучи свернута по определенному алгоритму, образует с наперед заданной точностью искомую поверхность. Процесс совмещения поверхности с плоскостью называется развертыванием поверхности, при этом, если поверхность совмещается с плоскостью без разрывов и складок, поверхность называется развертывающейся. К развертывающимся относятся все линейчатые поверхности и многогранники. Для неразвертывающихся поверхностей строят приближенные развертки.
Раздел 6. Развертка поверхностей Под разверткой поверхности понимают гибкую нерастяжимую оболочку (пленку), которая, будучи свернута по определенному алгоритму, образует с наперед заданной точностью искомую поверхность. Процесс совмещения поверхности с плоскостью называется развертыванием поверхности, при этом, если поверхность совмещается с плоскостью без разрывов и складок, поверхность называется развертывающейся. К развертывающимся относятся все линейчатые поверхности и многогранники. Для неразвертывающихся поверхностей строят приближенные развертки.
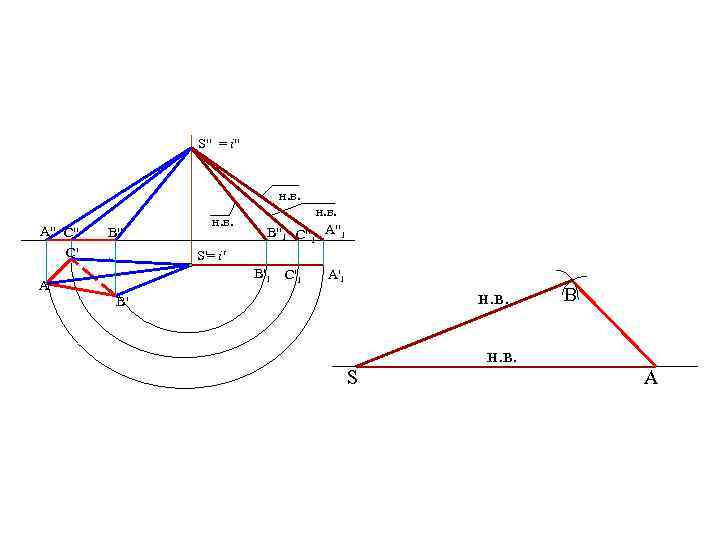
 • Способ триангуляции (треугольников) • Способ нормального сечения Способ триангуляции применяется для развертывания пирамидальных и конических поверхностей. Рассмотрим развертку поверхности пирамиды.
• Способ триангуляции (треугольников) • Способ нормального сечения Способ триангуляции применяется для развертывания пирамидальных и конических поверхностей. Рассмотрим развертку поверхности пирамиды.
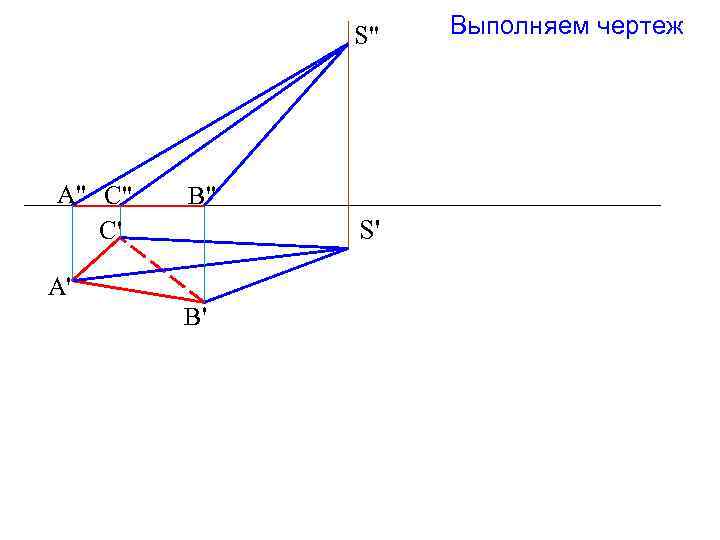 S" A" C" C' B" S' A' B' Выполняем чертеж
S" A" C" C' B" S' A' B' Выполняем чертеж
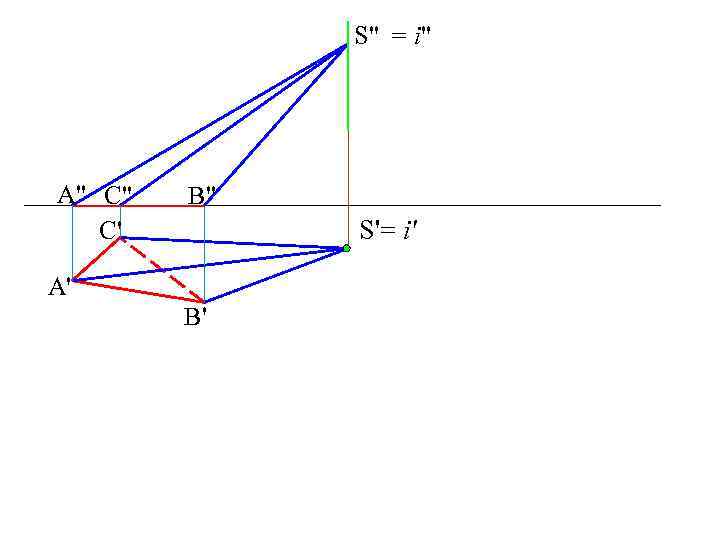 S" = i" A" C" C' B" S'= i' A' B'
S" = i" A" C" C' B" S'= i' A' B'
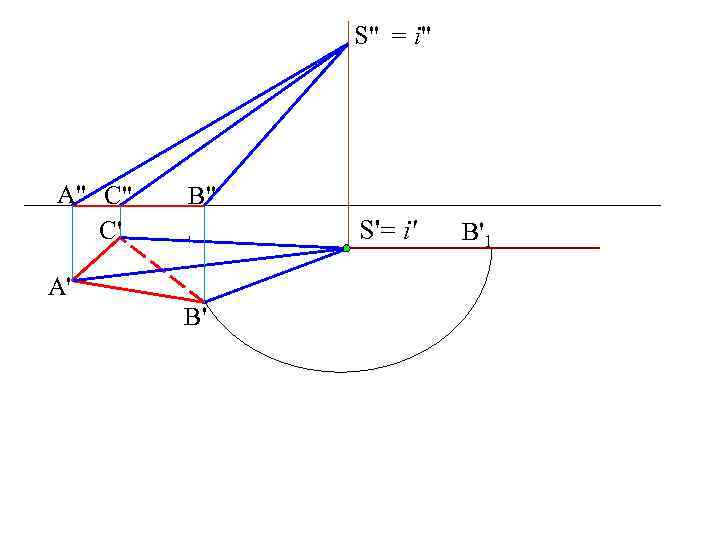 S" = i" A" C" C' B" S'= i' A' B' B'1
S" = i" A" C" C' B" S'= i' A' B' B'1
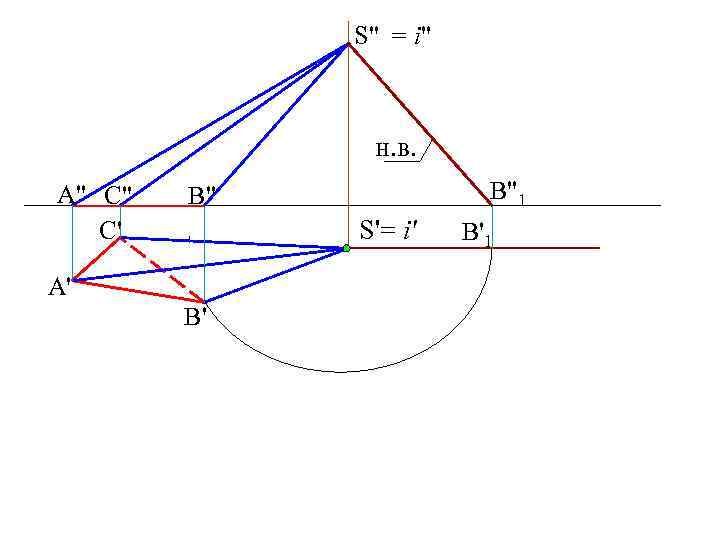 S" = i" н. в. A" C" C' B"1 B" S'= i' A' B' B'1
S" = i" н. в. A" C" C' B"1 B" S'= i' A' B' B'1
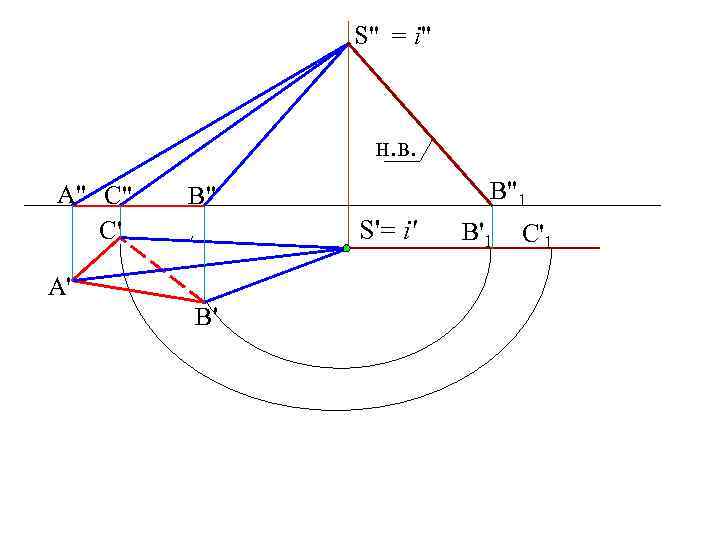 S" = i" н. в. A" C" C' B"1 B" S'= i' A' B' B'1 C'1
S" = i" н. в. A" C" C' B"1 B" S'= i' A' B' B'1 C'1
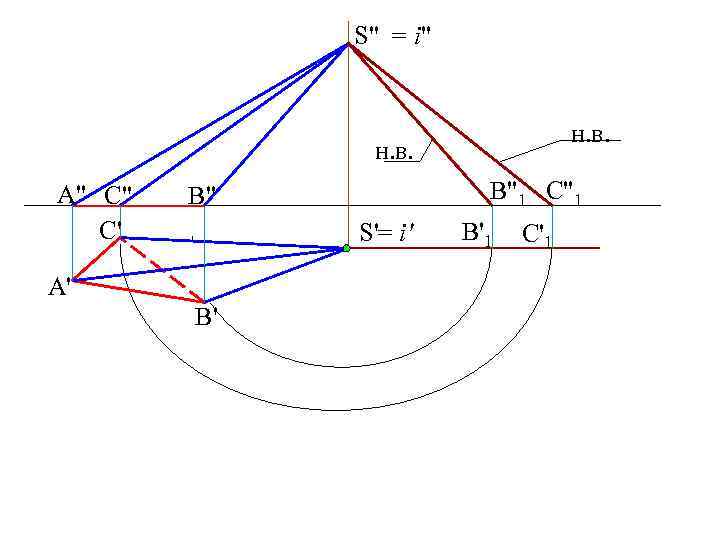 S" = i" н. в. A" C" C' B"1 C"1 B" S'= i' A' B' B'1 C'1
S" = i" н. в. A" C" C' B"1 C"1 B" S'= i' A' B' B'1 C'1
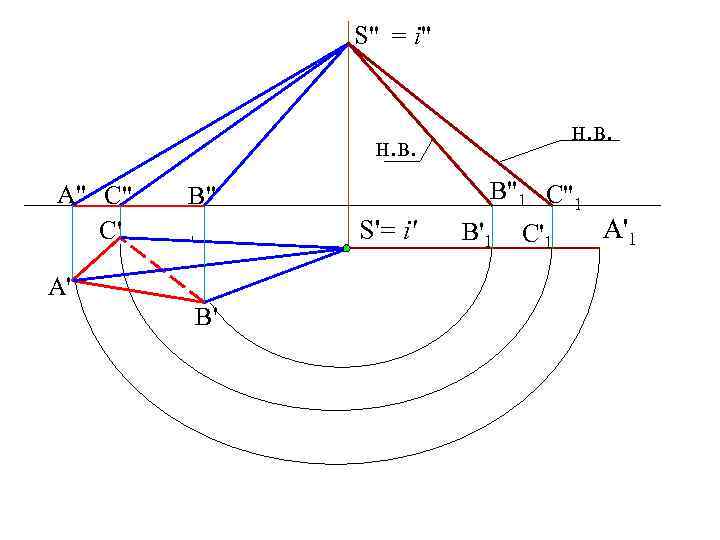 S" = i" н. в. A" C" C' B" S'= i' A' B' н. в. B"1 C"1 A'1 B'1 C'1
S" = i" н. в. A" C" C' B" S'= i' A' B' н. в. B"1 C"1 A'1 B'1 C'1
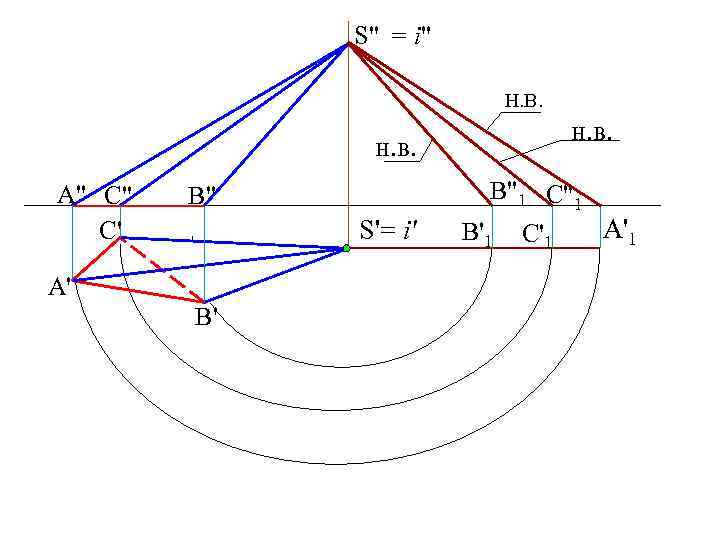 S" = i" Н. В. н. в. A" C" C' B" S'= i' A' B' н. в. B"1 C"1 A'1 B'1 C'1
S" = i" Н. В. н. в. A" C" C' B" S'= i' A' B' н. в. B"1 C"1 A'1 B'1 C'1
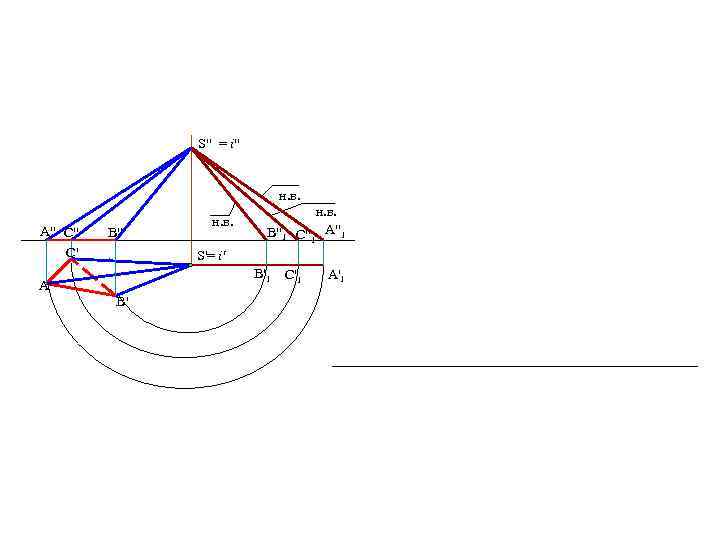 S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' B' C'1 A'1
S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' B' C'1 A'1
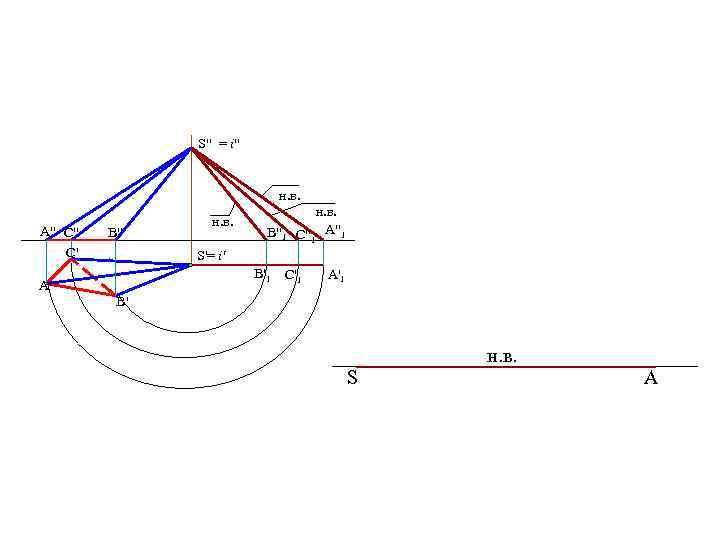 S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 B' S н. в. A
S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 B' S н. в. A
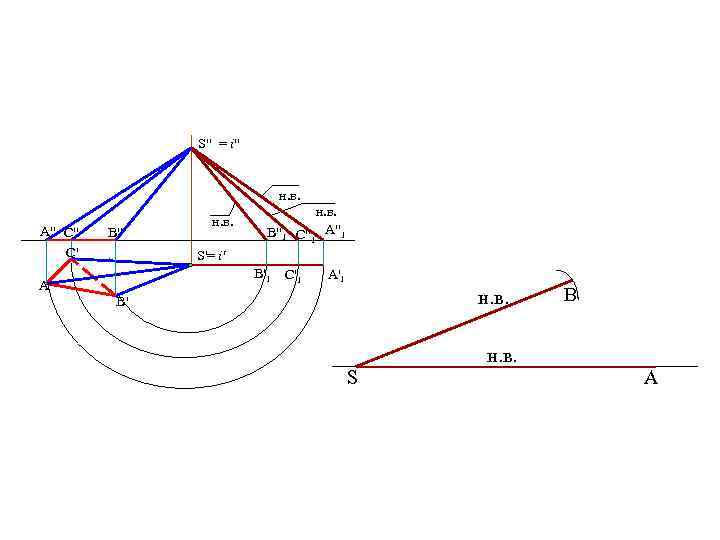 S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
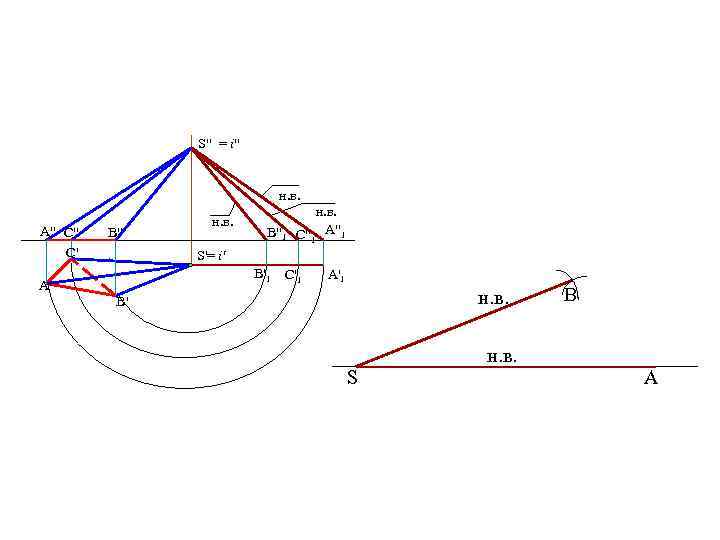 S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
 S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
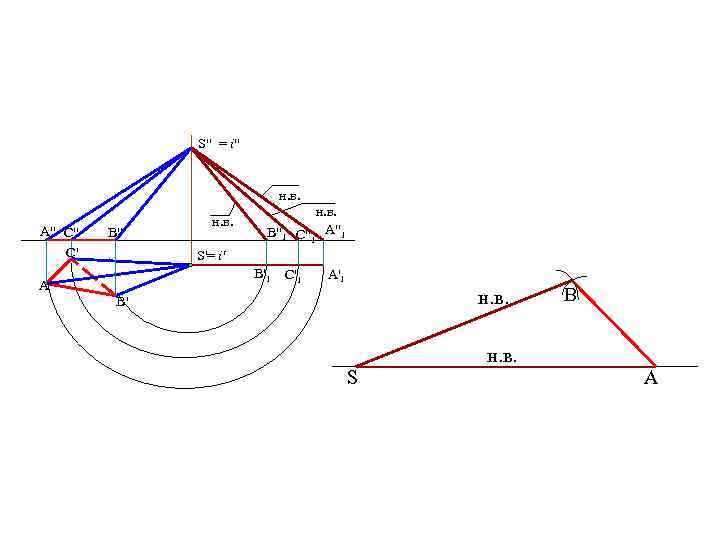 S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
S" = i" н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
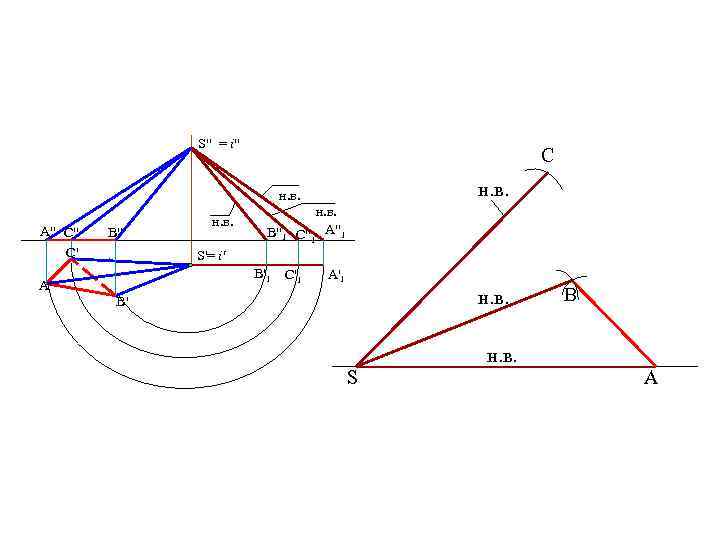 S" = i" C н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
S" = i" C н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
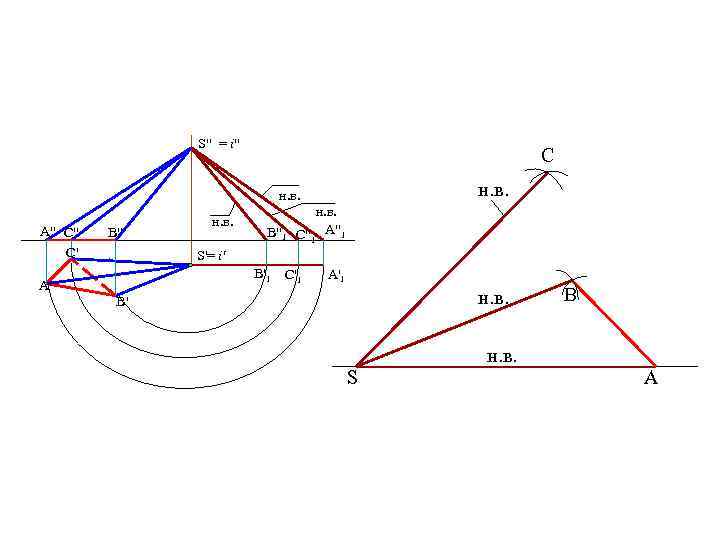 S" = i" C н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
S" = i" C н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
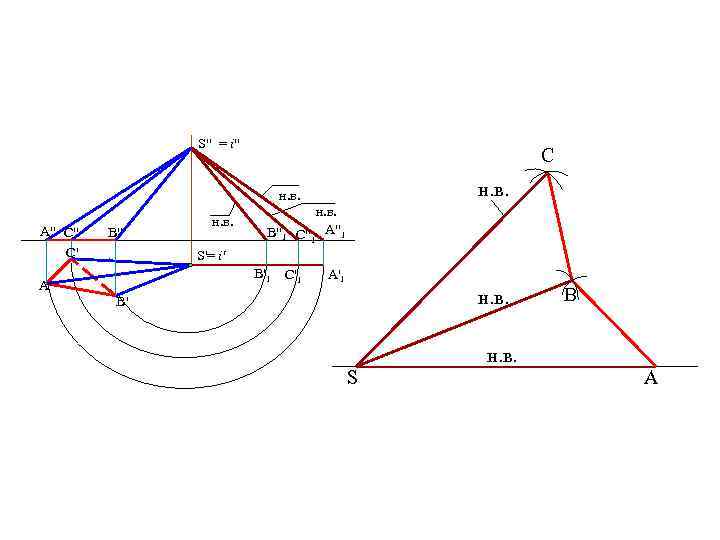 S" = i" C н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
S" = i" C н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
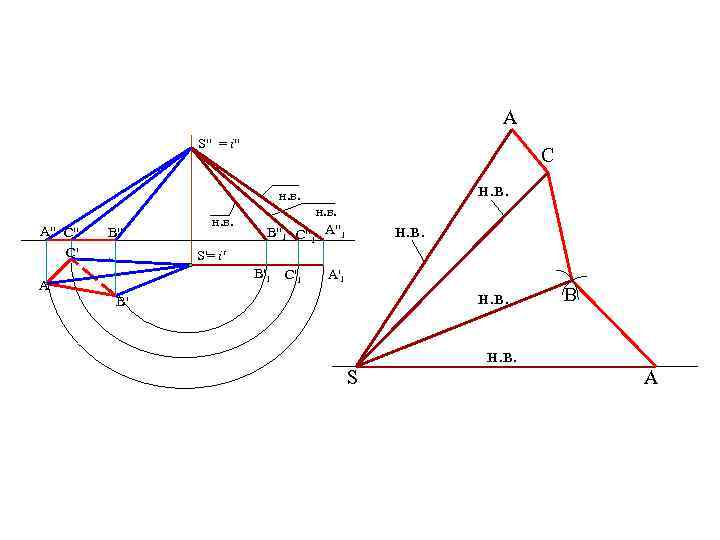 A S" = i" C н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 н. в. S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
A S" = i" C н. в. A" C" C' B" н. в. B"1 н. в. C"1 A"1 н. в. S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
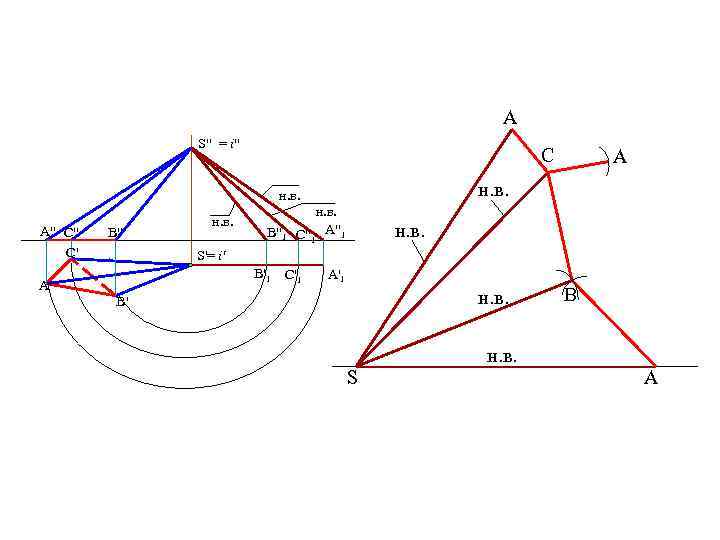 A S" = i" C н. в. A" C" C' B" н. в. B"1 A н. в. C"1 A"1 н. в. S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
A S" = i" C н. в. A" C" C' B" н. в. B"1 A н. в. C"1 A"1 н. в. S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
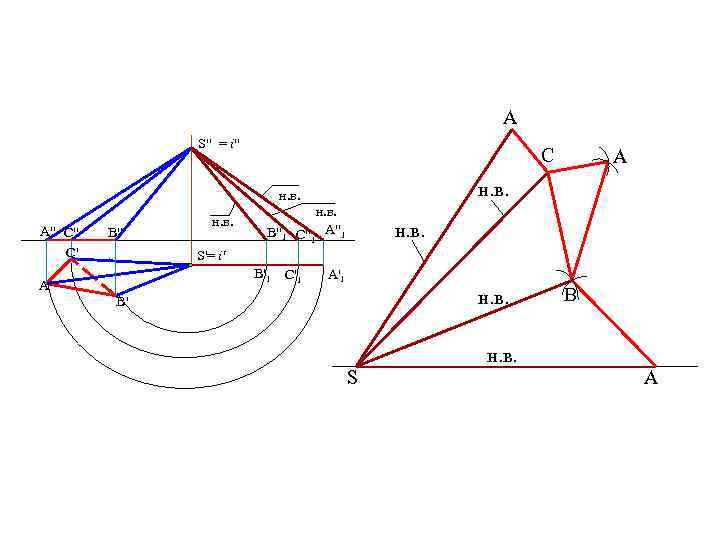 A S" = i" C н. в. A" C" C' B" н. в. B"1 A н. в. C"1 A"1 н. в. S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
A S" = i" C н. в. A" C" C' B" н. в. B"1 A н. в. C"1 A"1 н. в. S'= i' B'1 A' C'1 A'1 н. в. B' S B н. в. A
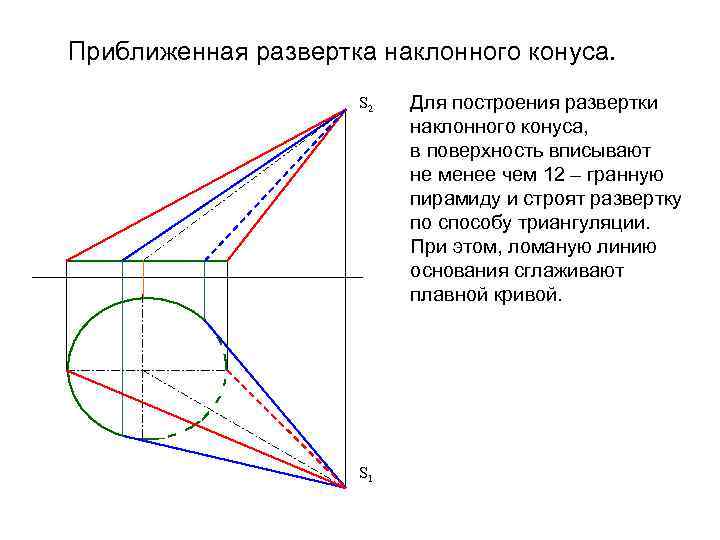 Приближенная развертка наклонного конуса. S 2 S 1 Для построения развертки наклонного конуса, в поверхность вписывают не менее чем 12 – гранную пирамиду и строят развертку по способу триангуляции. При этом, ломаную линию основания сглаживают плавной кривой.
Приближенная развертка наклонного конуса. S 2 S 1 Для построения развертки наклонного конуса, в поверхность вписывают не менее чем 12 – гранную пирамиду и строят развертку по способу триангуляции. При этом, ломаную линию основания сглаживают плавной кривой.
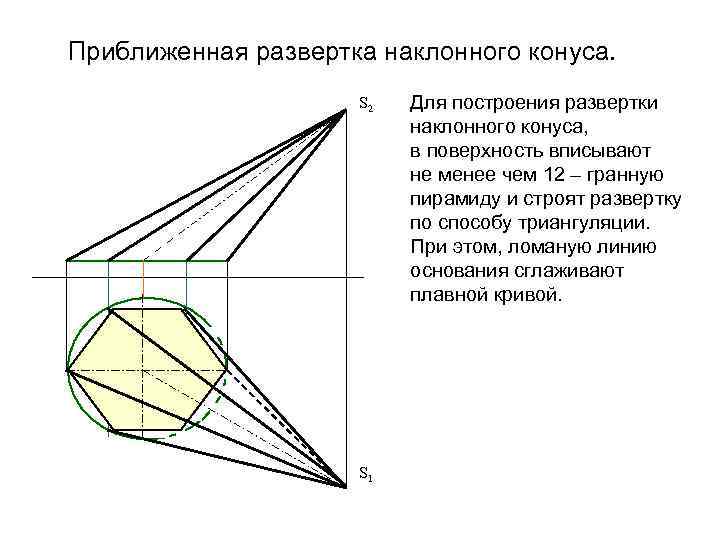 Приближенная развертка наклонного конуса. S 2 S 1 Для построения развертки наклонного конуса, в поверхность вписывают не менее чем 12 – гранную пирамиду и строят развертку по способу триангуляции. При этом, ломаную линию основания сглаживают плавной кривой.
Приближенная развертка наклонного конуса. S 2 S 1 Для построения развертки наклонного конуса, в поверхность вписывают не менее чем 12 – гранную пирамиду и строят развертку по способу триангуляции. При этом, ломаную линию основания сглаживают плавной кривой.
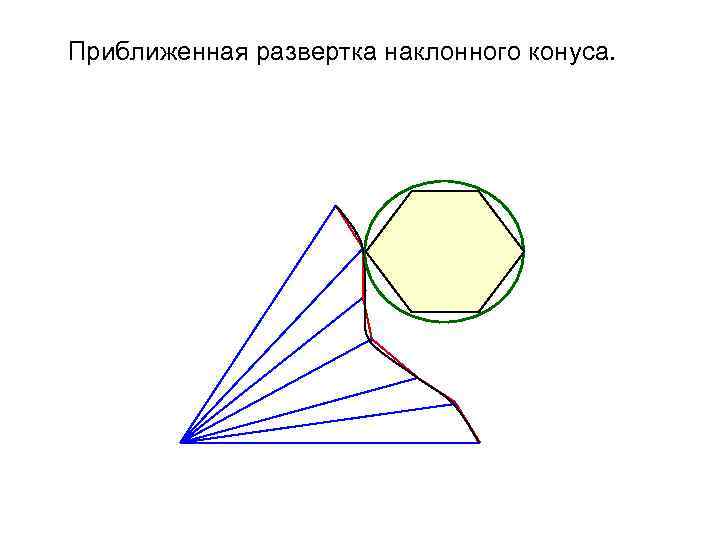 Приближенная развертка наклонного конуса.
Приближенная развертка наклонного конуса.
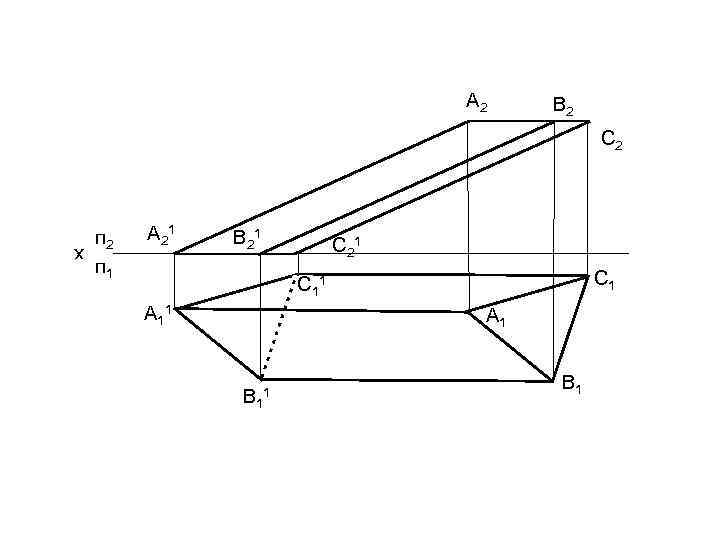
 Способ нормального сечения Применяется для развертывания призматических и цилиндрических поверхностей. Рассмотрим развертку поверхности призмы.
Способ нормального сечения Применяется для развертывания призматических и цилиндрических поверхностей. Рассмотрим развертку поверхности призмы.
 А 2 В 2 С 2 п 1 А 2 1 В 2 1 С 1 С 1 1 А 1 В 1 х
А 2 В 2 С 2 п 1 А 2 1 В 2 1 С 1 С 1 1 А 1 В 1 х
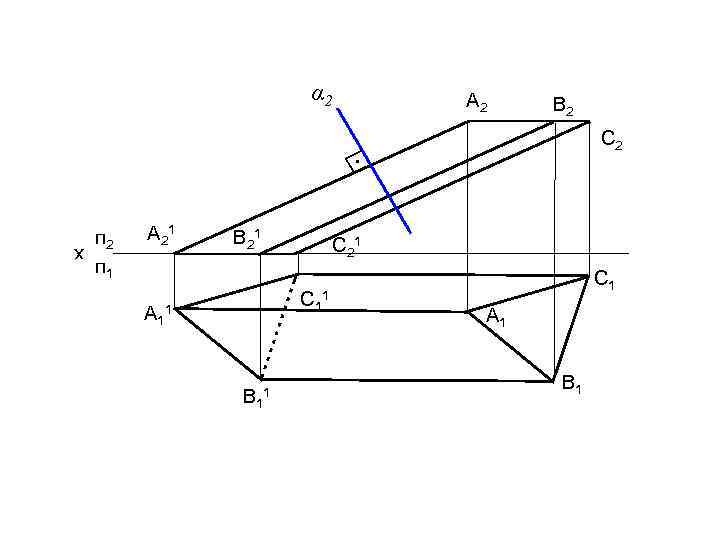 α 2 А 2 В 2 С 2 • п 2 п 1 А 2 1 В 2 1 С 1 А 1 1 В 1 1 С 1 1 А 1 В 1 х
α 2 А 2 В 2 С 2 • п 2 п 1 А 2 1 В 2 1 С 1 А 1 1 В 1 1 С 1 1 А 1 В 1 х
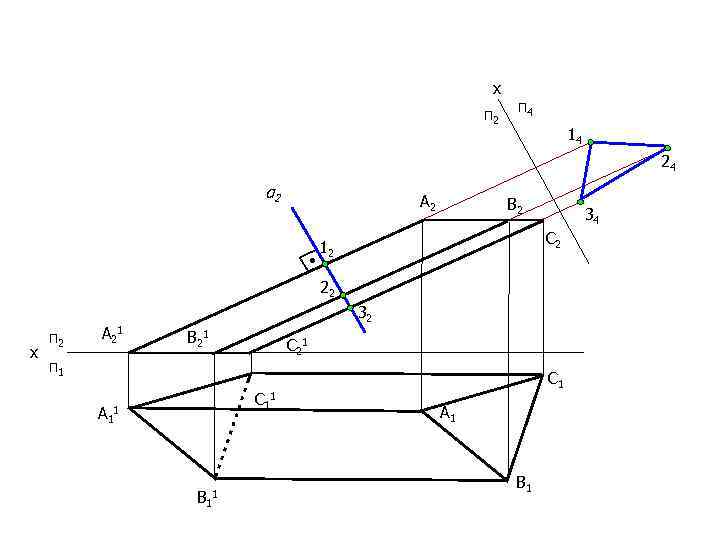 х п 2 п 4 14 24 α 2 А 2 • В 2 34 С 2 12 22 п 2 А 21 32 В 21 С 21 п 1 С 11 А 11 В 11 С 1 А 1 В 1 х
х п 2 п 4 14 24 α 2 А 2 • В 2 34 С 2 12 22 п 2 А 21 32 В 21 С 21 п 1 С 11 А 11 В 11 С 1 А 1 В 1 х
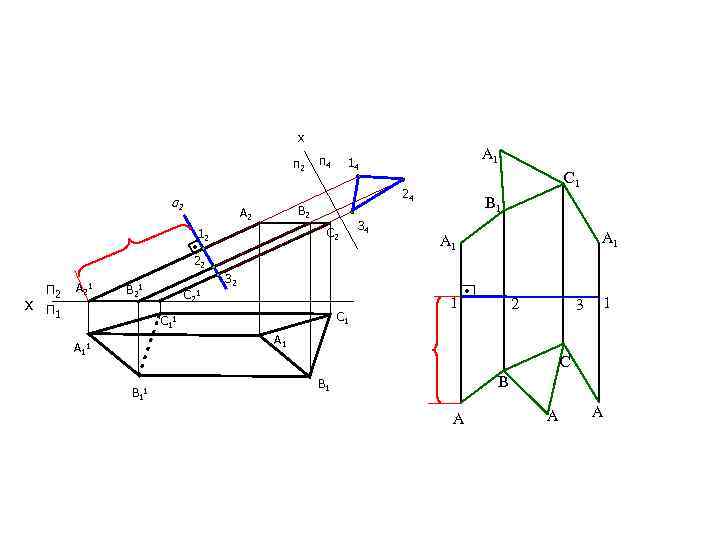 х п 2 В 2 А 2 С 2 12 • 22 А 21 А 1 14 С 1 24 α 2 п 1 п 4 34 B 1 32 В 21 С 2 С 1 1 А 1 1 • 2 3 1 А 11 С В 11 B В 1 А А А х
х п 2 В 2 А 2 С 2 12 • 22 А 21 А 1 14 С 1 24 α 2 п 1 п 4 34 B 1 32 В 21 С 2 С 1 1 А 1 1 • 2 3 1 А 11 С В 11 B В 1 А А А х
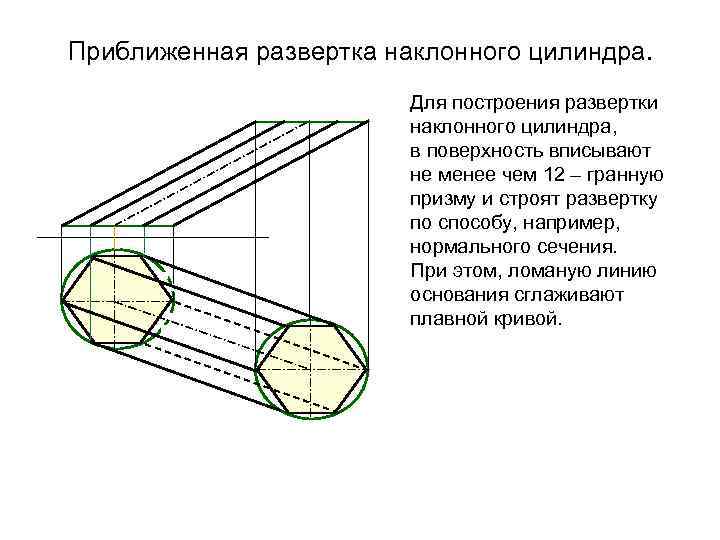 Приближенная развертка наклонного цилиндра. Для построения развертки наклонного цилиндра, в поверхность вписывают не менее чем 12 – гранную призму и строят развертку по способу, например, нормального сечения. При этом, ломаную линию основания сглаживают плавной кривой.
Приближенная развертка наклонного цилиндра. Для построения развертки наклонного цилиндра, в поверхность вписывают не менее чем 12 – гранную призму и строят развертку по способу, например, нормального сечения. При этом, ломаную линию основания сглаживают плавной кривой.


