Раздел № 6. Первообразная. Темы: 1. Определение первообразной. 2. Основное свойство первообразной. 3. Три правила нахождения первообразной. 4. Площадь криволинейной трапеции. 5. Формула Ньютона – Лейбница. 6. Решение задач. 7. Контрольная работа № 6.
Тема -1: Определение первообразной. Стр. 194.
Определение: • • Процесс отыскания производной по заданной функции называют дифференцированием, а обратную операцию, т. е. процесс отыскания функции по заданной производной – интегрированием. Первообразная (первичный образ) – F(х) F΄(х)=f(х)
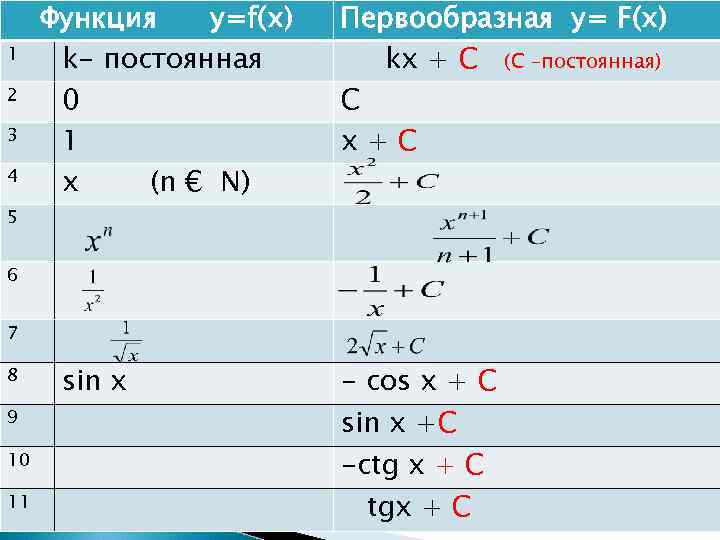
1 2 3 4 Функция у=f(х) k- постоянная 0 1 х (n € N) Первообразная у= F(х) kх + С (С –постоянная) С х+С 5 6 7 8 9 10 11 sin x - cos x + C sin x +C -ctg x + C tgx + C
Основное свойство первообразных Любая первообразная для функции f может быть записана в виде F(х)+С, где Спроизвольная постоянная. Пример. Доказать, что для функции cos x первообразной является функция F(x)=sinx +C Доказательство.
Признак постоянства функции Если F´(х)=0 на некотором промежутке, то функция F(х)- постоянная на этом промежутке. Пример. Найти производную для функций:
Самостоятельная работа из сборника экзамен. заданий (стр. 6, 8, 11, 13 Вариант № 2 Вариант № 1 1. Найти общий вид первообразной для функции: f(х)=х⁴+3 х²+5 2. Найти первообразную функции: f(х)=4+6 х², используя таблицу и правило нахождения первообразной суммы функций, если F(2) величина отрицательная. (стр. 11, в-4) 3. Вычислить площадь фигуры, ограниченной графиком функции f(х)=х²+5 х+6, прямыми х=-1, х=2, у=0 (в-5, стр. 13) 1. Найти общий вид первообразной для функции: f(х)=х³-3 х²+х-1 2. Найти первообразную функции: f(х)=х²-5, используя таблицу нахождения первообразной, если функция F(х) проходит через точку (3; 4). (в-9, стр. 19) 3. Вычислить площадь фигуры, ограниченной графиком функции у=0, х=-2, х=-1 f(х)=х²-6 х+8, если она принимает только положительные значения на промежутке х€[-2; -1] (в-11, стр. 13)
Самопроверка самостоятельной работы из сборника экзамен. заданий (стр. 6, 8, 11, 13 Вариант № 2 Вариант № 1 1. Ответ: общий вид первообразной для функции: f(х)=х⁴+3 х²+5 является F(х)=х⁵/5 +х³+5 х+С 1. Ответ: общий вид первообразной для функции: f(х)=х³-3 х²+х-1 является F(х)=х⁴/4 -х³+х²/2+С (стр. 8, в-2) (стр. 6, в-1) 2. Ответ: первообразной функции: f(х)=4+6 х² является функция F(х)= (в-9, стр. 19) (стр. 11, в-4) 3. Ответ: площадь фигуры равна S=28, 5 кв. ед. (в-5, стр. 13) 2. Ответ: первообразную функции: f(х)=х²-5 является функция F(х)=х³/3 -х5+10 3. Ответ: площадь фигуры равна (в-11, стр. 13)
Определение 1. ( стр. 195) Составить таблицу первообразных. (с. 196) Пример № 1 (стр. 194) Записать правила отыскания первообразных. Пример № 2, № 3 Стр. 197. Записать теорему на стр. 199.
Неопределенный интеграл. Стр. 200 определение-2, таблица интегралов. Стр. 201. правила вычисления интегралов. пример -6 (а, б, в)
Определенный интеграл. Вычисление площади криволинейной трапеции. Задача-1 - устно. Рисунок 155 - Стр. 202. Определение определенного интеграла, формула (стр. 205).
Формула Ньютона - Лейбница. Стр. 206 рис 157, формула (1) Этапы решения задач на нахождение площади криволинейной трапеции. -(с. 207). Теорема - Стр. 208. Пример-1. - стр. 208. Пример-2. Пример -3 стр. 209 (рис. 159) Свойство-1, 2, 3. (рис. 160)
Вычисление площадей плоских фигур с помощью определенного интеграла. Фигура Р (рис. 161, а) Формула -3 Пример-4, 5 (с. 211), рис 162.
Скачать презентацию Раздел 6 Первообразная Темы 1 Определение первообразной
1- Первообразная Определение.ppt