Раздел 3 Теория пределов 1 1 Предел

Раздел 3: Теория пределов 1

1. Предел функции Пусть f(x) – функция, определенная на множестве Х; А и а –числа. Опр. Число А называется пределом функции f(x) при x a, если >0 такая -окрестность точки а U (a), что | f(x) -A|< x U (a). Эквивалентные формы записи: или f(x) А при x a. Опр. , если >0 = ( ): | f(x) -A|< |x|> . 2

Замечания: 1. Функция может быть меньше своего предела. 1. Функция может быть больше своего предела. 1. Функция может колебаться вокруг своего предела. 3

Бесконечно малые и бесконечно большие функции (БМФ и ББФ) Опр. Функция f(x) называется бесконечно малой при x a, если >0 U (a), что |f(x)|< при x U (a) или Опр. Функция f(x) называется бесконечно большой при x a, если >0 U (a), что |f(x)|> при x U (a) или 4

Лемма (связь БМФ и ББФ). Теорема (свойства БМФ). 1. Алгебраическая сумма (+ и -) конечного числа б. м. функций при x a есть б. м. функция при x a. 2. Произведение б. м. функций при x a есть б. м. функция при x a. 5

2. Свойства пределов Теорема 1. Число A является пределом функции f(x) при x a, тогда и только тогда, когда функция f(x)-A является бесконечно малой: 6

Свойства пределов Теорема 2. Предел постоянной функции f(x) C при x a равен самой постоянной: 7

Свойства пределов Теорема 3. Если каждое слагаемое алгебр. суммы конечного числа функций имеет предел при x a, то предел этой суммы при x a и равен сумме пределов слагаемых: 8

Свойства пределов Теорема 4. Если каждый из сомножителей произведения конечного числа функций имеет предел при x a, то предел произведения при x a и равен произведению пределов сомножителей: 9

Свойства пределов (продолжение) Теорема 6. Если функция f(x) имеет предел при x a и 11

Свойства пределов Теорема 7. Если f(x) – элементарная ( «школьная» ) функция и число a принадлежит ее области определения, то предел вычисляется прямой подстановкой: 12

Следствия Следствие 1. Постоянный множитель можно выносить за знак предела: Следствие 2. Если функция f(x) имеет предел при x a, то предел при x a целой положительной степени n ее равен такой же степени предела этой функции: 13

Следствия (продолжение) Следствие 3. Если функция f(x) имеет предел при x a, отличный от 0, то предел при x a обратной ей по величине функции равен обратной величине предела данной функции: 14

3. «Замечательные» пределы Замечание. Не всякая функция имеет предел (даже ограниченная). Пример: Теорема 1. (1 -й замечательный предел) Теорема 2. (2 -й замечательный предел) 15

Примеры Нельзя использовать 1 -й замечательный предел, т. к. - тоже 1 -й замечательный предел)

4. Раскрытие неопределенностей Опр. Случаи, в которых подстановка предельного значения в функцию не дает значения предела, называют неопределенностями. Они бывают следующих типов: Устранить неопределенности часто удается с помощью алгебраических преобразований. 18

1 -й тип В числителе и знаменателе сложные степенные или показательные функции. Для степенных функций – вынести за скобку в числителе и знаменателе дроби х с наибольшим показателем степени среди всех слагаемых дроби; для показательных функций – за скобку выносится наиболее быстро возрастающее слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется. 19

2 -й тип а) многочлены Необходимо разложить на множители и числитель, и знаменатель дроби, исходя из того, что, если a – корень многочлена P(x), то P(x) делится на (x-a). Часто помогают «формулы сокращенного умножения» . После сокращения дроби неопределенность устраняется. 20

2 -й тип б) тригонометрические Необходимо упростить выражение, чтобы свести к 1 -му замечательному пределу 21

3 -й тип Если функция представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится ко 2 -му типу после приведения дробей к общему знаменателю. Если функция представляет собой алгебраическую сумму иррациональных выражений (корней), то неопределенность устраняется или приводится к 1 -му типу путем домножения и деления функции на одно и то же (сопряженное) выражение, приводящее к формулам сокращенного умножения. 22

Примеры 3 -го типа 23

4 -й тип Сводить ко 2 -му замечательному пределу 24

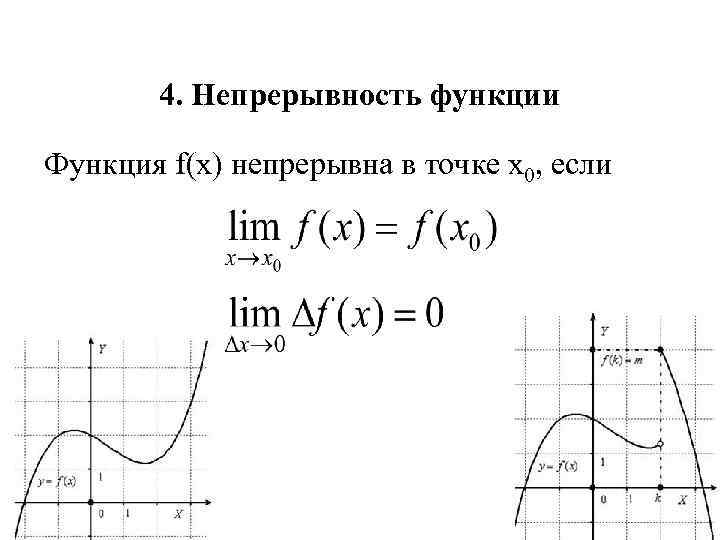4. Непрерывность функции Функция f(x) непрерывна в точке х0, если

Свойства непрерывных функций 1. Все основные функции непрерывны в области их определения. 2. Функция является непрерывной на интервале (a; b), если она непрерывна в каждой точке этого интервала.

Свойства непрерывных функций 3. Если функции f(x) и g(x) непрерывны в x 0, то f(x)+g(x), f(x)-g(x), f(x)/g(x) непрерывны в x 0. 4. Функция f(g(x)) – непрерывная.

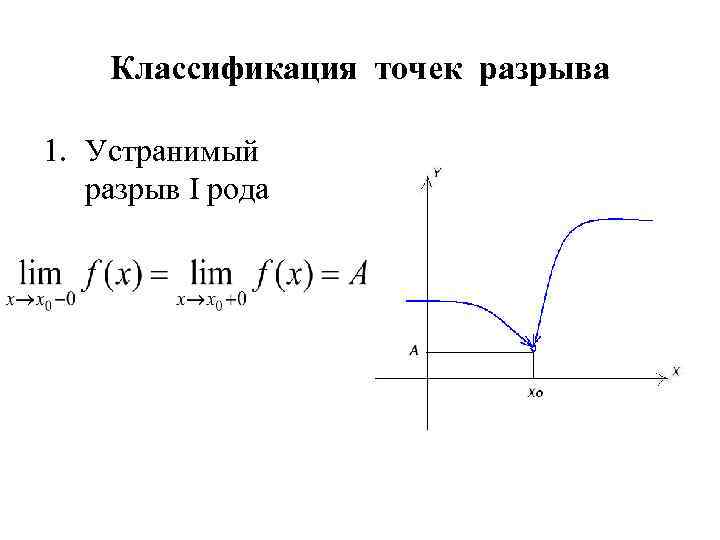Классификация точек разрыва 1. Устранимый разрыв I рода

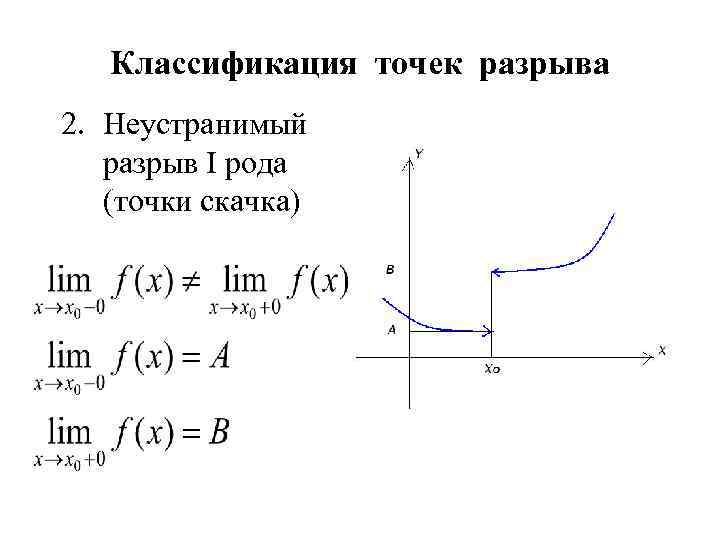Классификация точек разрыва 2. Неустранимый разрыв I рода (точки скачка)

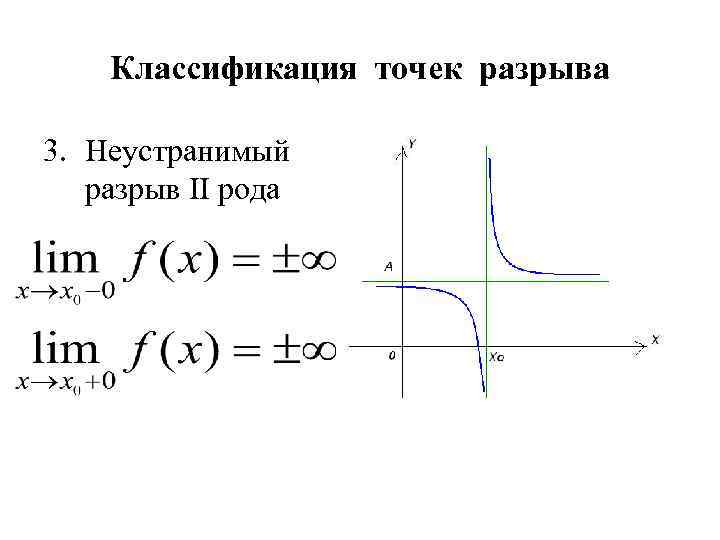Классификация точек разрыва 3. Неустранимый разрыв II рода

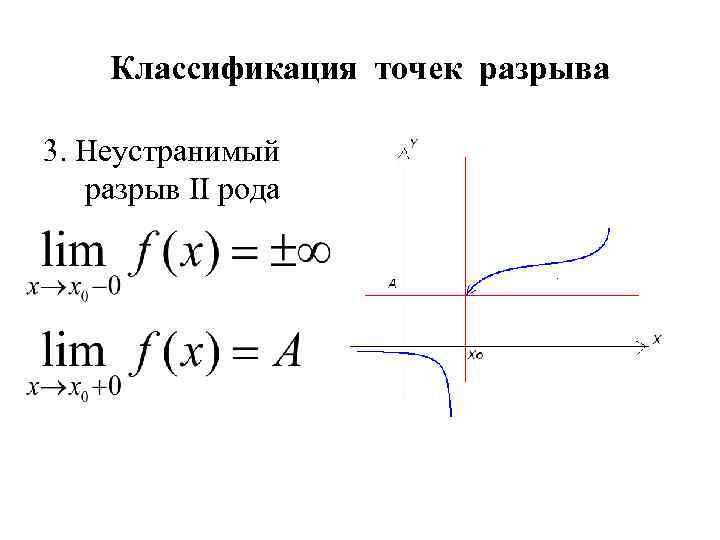Классификация точек разрыва 3. Неустранимый разрыв II рода

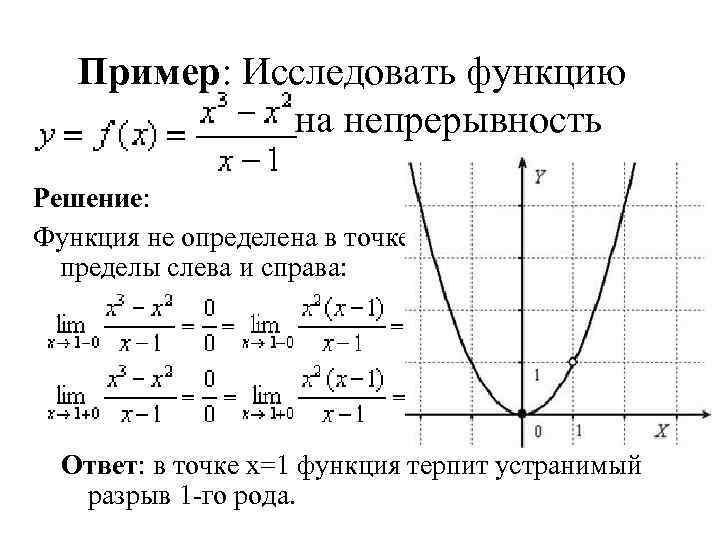Пример: Исследовать функцию на непрерывность Решение: Функция не определена в точке х=1. Найдем пределы слева и справа: Ответ: в точке х=1 функция терпит устранимый разрыв 1 -го рода.

Пример 1. • Определить количество точек разрыва функции 33

Пример 2. Для функции точка х=-2 является точкой… • а) разрыва второго рода; • б) непрерывности; • в) разрыва первого рода; • г) устранимого разрыва 34

Пример 3. Для функции точка х=1 является точкой… • а) разрыва второго рода; • б) непрерывности; • в) разрыва первого рода; • г) устранимого разрыва 35

4. Дифференциальное исчисление функции одной переменной Дифференциальное исчисление – раздел математики, в котором изучаются производные и дифференциалы функций и их применение к исследованию функций.

Производная функции 1. Определение производной функции. Необходимое условие существования производной Пусть y = f(x) определена в точке x 0 и некоторой ее окрестности. Придадим x 0 приращение x такое, что x 0 + x D(f). Функция при этом получит приращение f(x 0) = f(x 0 + x) – f(x 0).

ОПРЕДЕЛЕНИЕ. Производной функции y = f(x) в точке x 0 называется предел отношения приращения функции в этой точке к приращению аргумента x, при x 0 (если этот предел существует и конечен), т. е. Обозначают:

Производной функции y = f(x) в точке x 0 справа (слева) называется (если этот предел существует и конечен). Обозначают: – производная y = f(x) в точке x 0 справа, – производная y = f(x) в точке x 0 слева.

ТЕОРЕМА 1 (необходимое и достаточное условие существования производной). Функция y = f(x) имеет производную в точке x 0 в этой точке существуют и равны между собой производные функции справа и слева. Причем ТЕОРЕМА 2 (необходимое условие существования производной функции в точке). Если функция y = f(x) имеет производную в точке x 0 , то функция f(x) в этой точке непрерывна. Замечание. Непрерывность функции в точке x 0 не является достаточным условием существования в этой точке производной функции. Например, функция y = | x | непрерывна на всей области определения, но не имеет производной в точке x 0 = 0.

Соответствие x 0 f (x 0) является функцией, определенной на множестве D 1 D(f). Ее называют производной функции y = f(x) и обозначают Операцию нахождения для функции y = f(x) ее производной функции называют дифференцированием функции f(x).

Физический смысл производной Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная f (x) – скорость изменения величины y относительно величины x. ПРИМЕРЫ. а) Пусть S = S(t) – расстояние, проходимое точкой за время t. Тогда производная S (t 0) – скорость в момент времени t 0. б) Пусть q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t. Тогда q (t 0) – скорость изменения количества электричества в момент времени t 0, т. е. сила тока в момент времени t 0. в) Пусть m = m(x) – масса отрезка [a ; x]. Тогда m (x) – скорость изменения массы в точке x 0, т. е. линейная плотность в точке x 0.

Геометрический смысл производной Пусть ℓ – некоторая кривая, M 0 – точка на кривой ℓ. Любая прямая, пересекающая ℓ не менее чем в двух точках, называется секущей. Касательной к кривой ℓ в точке M 0 называется предельное положение секущей M 0 M 1, если точка M 1 стремится к M 0, двигаясь по кривой. Очевидно, что если касательная к кривой в точке M 0 существует, то она единственная.

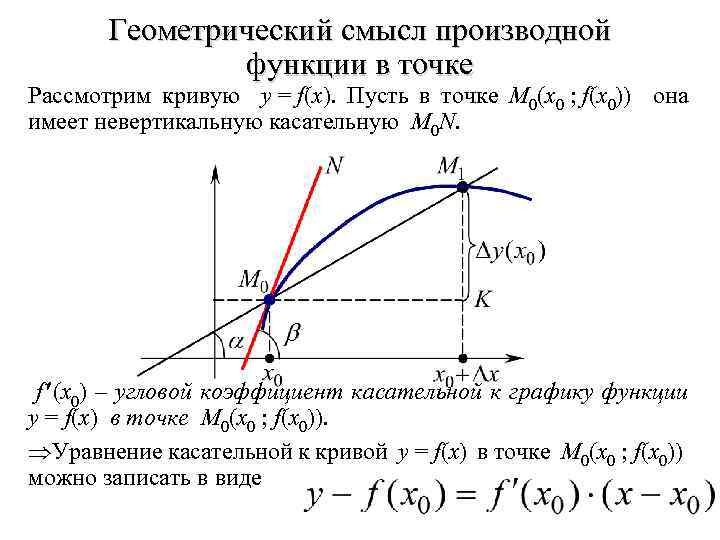Геометрический смысл производной функции в точке Рассмотрим кривую y = f(x). Пусть в точке M 0(x 0 ; f(x 0)) она имеет невертикальную касательную M 0 N. f (x 0) – угловой коэффициент касательной к графику функции y = f(x) в точке M 0(x 0 ; f(x 0)). Уравнение касательной к кривой y = f(x) в точке M 0(x 0 ; f(x 0)) можно записать в виде

Замечания. 1) Прямая, проходящая через точку M 0 перпендикулярно касательной, проведенной к кривой в точке M 0, называется нормалью к кривой в точке M 0. Т. к. для угловых коэффициентов перпендикулярных прямых справедливо равенство k 1 k 2 = – 1 , то уравнение нормали к y = f(x) в точке M 0(x 0 ; f(x 0)) будет иметь вид , если f (x 0) 0. Если же f (x 0) = 0, то касательная к кривой y = f(x) в точке M 0(x 0 ; f(x 0)) будет иметь вид y = f(x 0), а нормаль x = x 0.

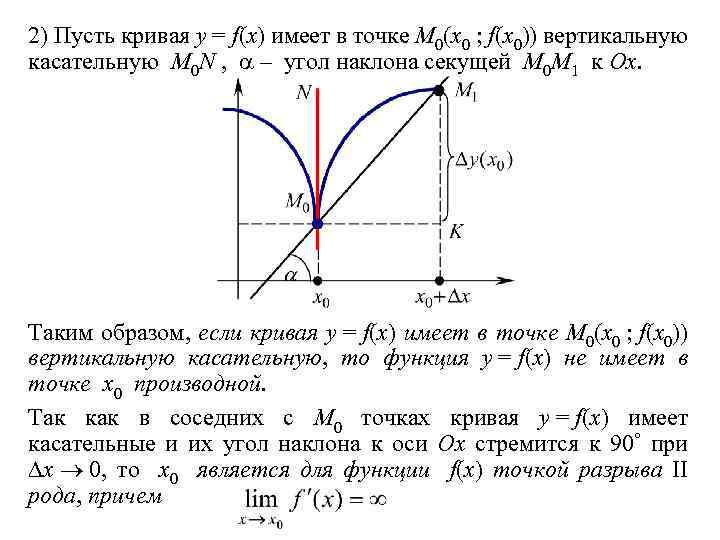2) Пусть кривая y = f(x) имеет в точке M 0(x 0 ; f(x 0)) вертикальную касательную M 0 N , – угол наклона секущей M 0 M 1 к Ox. Таким образом, если кривая y = f(x) имеет в точке M 0(x 0 ; f(x 0)) вертикальную касательную, то функция y = f(x) не имеет в точке x 0 производной. Так как в соседних с M 0 точках кривая y = f(x) имеет касательные и их угол наклона к оси Ox стремится к 90 при x 0, то x 0 является для функции f(x) точкой разрыва II рода, причем

Правила дифференцирования 1) Производная константы равна нулю, т. е. C = 0, где С – константа. 2) Производная суммы (разности) равна сумме (разности) производных, т. е. 3) Производная произведения находится по правилу: Замечание. Формула дифференцирования произведения может быть легко обобщена на случай большего числа множителей. Например,

Правила дифференцирования , где С – константа. 5) Производная дроби находится по правилу: 6) Если функция (t) имеет производную в точке t, а функция f(u) имеет производную в точке u = (t), то сложная функция y = f( (t)) имеет производную в точке t, причем (правило дифференцирования сложной функции).

Правила дифференцирования 7) ТЕОРЕМА 3 (о производной обратной функции). Пусть функция y = f(x) имеет производную в точке x 0, причем f (x 0) 0. Если существует обратная функция x = (y), то она имеет производную в точке y 0 = f(x 0) и

По определению и с помощью правил дифференцирования находят производные основных элементарных функций (так называемая «таблица производных» ). Производная любой элементарной функции находится с помощью таблицы производных и правил дифференцирования.

Таблица производных элементарных функций 1) 2) 3) 4) 5) 6) 7) 8) 9) 9) (С)´= 0, C = const; (x )´ = x -1, R, x > 0; (xn)´ = n xn-1, n N, x R; (ax)´ = axlna, a > 0, a ≠ 1, x R; (ex)´ = ex, x R; . . (sin x) = cos x, x R; (cos x) = - sin x, x R; (tg x) = 1/ cos 2 x, х ≠ π/2 + πn, n Z; 10) (ctg x) = - 1/ sin 2 x, х ≠ πn, n Z; 12)

Логарифмическое дифференцирование u(x), v(x) – дифференцируемые в точке х функции. Пример 1. Пример 2.

Производная n-ого порядка Пусть f(x) определена в U (x 0) и имеет производную f (x) в каждой точке этого интервала. Если в точке х0 существует производная от f (x), то она называется второй производной от функции f(x) в этой точке и обозначается Аналогично определяется производная f (n) (x) любого порядка n =1, 2, … Если в U (x 0) существует f (n-1)(x) (при этом под производной нулевого порядка подразумевается сама функция), то n = 1, 2, 3, ….

Функцию, имеющую в каждой точке множества Х производные до n-ого порядка включительно, называют n раз дифференцируемой на множестве Х. Пусть функции f(x) и g(x) имеют в точке х производные n-ого порядка. Тогда функция Аf(x) + Вg(x), где А и В постоянные, также имеет производную в точке х, причем (Аf(x) + Вg(x))(n) = Аf (n)(x) + Вg (n)(x). y '' = 2 (x + a) - 3, y ''' = - 2 3 (x + a) - 4, …

Основные формулы 1) y = x ; y (n) = ( -1)… ( - (n-1)) x - n. y = x -1, y = ( -1)x -2, y = ( -1)( -2) x -3 … В частности, если = m N, то 2) y = ax; y (n) = ax (ln a)n. y =ax ln a, y = ax (ln a)2, y = ax (ln a)3, … В частности (еx)(n) = ех. 3) y ' = ((x + a) - 1)' = -(x + a)-2, y '' = 2 (x + a)-3, y ''' = -2 3 (x + a)-4, …

Основные формулы 4) y = ln(x+а); y (n) = (– 1)n– 1(n– 1)!(x+а)–n y = (x +а) – 1, y = – (x +а) – 2, y = 2(x +а) – 3, y (4) = – 2· 3(x +а) – 4 , … 5) y = sin αx; y (n) = αn sin(αx+n· /2) y = α cos αx = α sin(αx+ /2), y = α 2 cos(αx+ /2) = α 2 sin(αx+2· /2), y = α 3 cos(αx + 2· /2) = α 3 sin(αx+3· /2), … 6) y = cos αx; y (n) = αn cos(αx+n· /2) y = – α sin αx = α cos(αx+ /2), y = – α 2 sin(αx+ /2) = α 2 cos(αx + 2· /2), y = – α 3 sin(αx+2· /2) = α 3 cos(αx + 3· /2), . . .

n-ая производная произведения двух функций (формула Лейбница) Пусть функции f(x) и g(x) имеют в точке х производные n-ого порядка. (f(x) g(x))(n) = ? По индукции можно доказать, что - формула Лейбница где

y = (x 2+3 x+5) sin x, y(13) = ? Пример 3. Применим формулу Лейбница, положив в ней f(x) = sin x, g(x) = (x 2+3 x+5). Тогда = sin(x +13π /2) (x 2+3 x+5) + 13 sin (x +12π /2) (2 x+3) + 78 sin (x +11π /2) 2 = = cos x (x 2+3 x+5) + 13 sin x (2 x+3) + 78 ( - cos x) 2 = = (x 2 +3 x -151) cos x + 13 (2 x+3) sin x.