Раздел 2. Компьютерное моделирование Лекция 4.



















Моделирование инфокоммуникационных систем_Л3.pptx
- Количество слайдов: 26
 Раздел 2. Компьютерное моделирование Лекция 4. Статистическое моделирование
Раздел 2. Компьютерное моделирование Лекция 4. Статистическое моделирование
 Статистическое моделирование на ЭВМ Компьютерное моделирование – деятельность по разработке программных моделей систем, выполнение этих программ на компьютере и анализ результатов по исследованию поведения моделей Области компьютерного моделирования: n имитационное моделирование l GPSS, Vis. Sim, Any. Logic, Dy. Mo. La, Dynast, Multisim, MBTY, Simulink n статистическое моделирование l метод решения вероятностных и детерминированных задач, основанный на эффективном использовании случайных чисел и законов теории вероятностей
Статистическое моделирование на ЭВМ Компьютерное моделирование – деятельность по разработке программных моделей систем, выполнение этих программ на компьютере и анализ результатов по исследованию поведения моделей Области компьютерного моделирования: n имитационное моделирование l GPSS, Vis. Sim, Any. Logic, Dy. Mo. La, Dynast, Multisim, MBTY, Simulink n статистическое моделирование l метод решения вероятностных и детерминированных задач, основанный на эффективном использовании случайных чисел и законов теории вероятностей
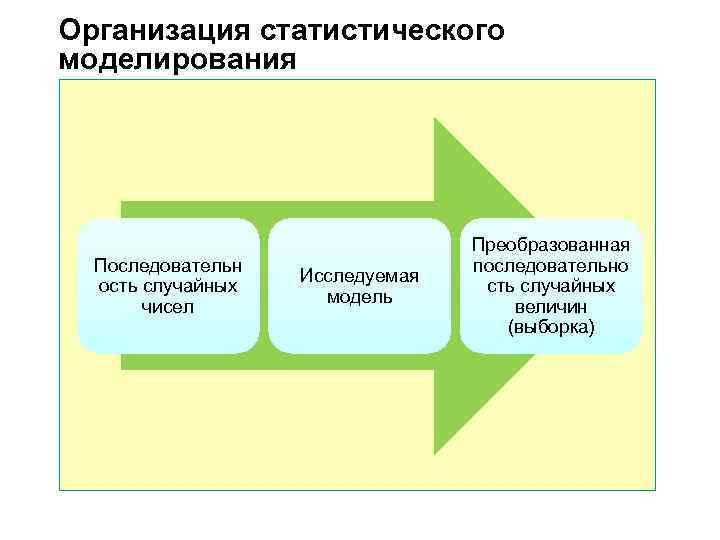
 Организация статистического моделирования Преобразованная Последовательн последовательно Исследуемая ость случайных модель чисел величин (выборка)
Организация статистического моделирования Преобразованная Последовательн последовательно Исследуемая ость случайных модель чисел величин (выборка)
 Организация статистического моделирования n При имитационном моделировании стохастических систем имитируются: l случайное событие с заданными вероятностями, l случайные величины с заданными распределениями, l случайные процессы с заданными характеристиками (математическое ожидание, дисперсия, корреляционная функция). n Для имитации случайной величины с заданным распределением нужно иметь генератор (датчик) случайных чисел (ДСЧ), генерирующий числа с заданным законом
Организация статистического моделирования n При имитационном моделировании стохастических систем имитируются: l случайное событие с заданными вероятностями, l случайные величины с заданными распределениями, l случайные процессы с заданными характеристиками (математическое ожидание, дисперсия, корреляционная функция). n Для имитации случайной величины с заданным распределением нужно иметь генератор (датчик) случайных чисел (ДСЧ), генерирующий числа с заданным законом
 Организация статистического моделирования Генерирование случайных чисел на ЭВМ с заданным законом распределения: n Получают последовательность равномерно распределенных на интервале [0, 1] псевдослучайных чисел, n Из равномерно распределенной последовательности получают последовательность псевдослучайных чисел с заданным законом распределения в заданном интервале.
Организация статистического моделирования Генерирование случайных чисел на ЭВМ с заданным законом распределения: n Получают последовательность равномерно распределенных на интервале [0, 1] псевдослучайных чисел, n Из равномерно распределенной последовательности получают последовательность псевдослучайных чисел с заданным законом распределения в заданном интервале.
 Генерирование базового распределения Типы датчиков случайных чисел n Табличные l просто таблица случайных чисел n Физические l специальное радиоэлектронное устройство, содержащее источник электронного шума n Программные l числа получают с помощью некоторой рекуррентной формулы, где каждое следующее значение образуется из предыдущего предыдущих путем применения некоторого алгоритма
Генерирование базового распределения Типы датчиков случайных чисел n Табличные l просто таблица случайных чисел n Физические l специальное радиоэлектронное устройство, содержащее источник электронного шума n Программные l числа получают с помощью некоторой рекуррентной формулы, где каждое следующее значение образуется из предыдущего предыдущих путем применения некоторого алгоритма
 Генерирование базового распределения Метод середины квадрата n произвольное число, меньшее 1 возводят в квадрат, n отбрасывают цифры с обоих концов, n оставшуюся часть используют как случайное число. n процесс повторяют. Пример
Генерирование базового распределения Метод середины квадрата n произвольное число, меньшее 1 возводят в квадрат, n отбрасывают цифры с обоих концов, n оставшуюся часть используют как случайное число. n процесс повторяют. Пример
 Генерирование базового распределения Мультипликативный конгруэнтный метод n расчет по формуле: l где mod – операция получения остатка от деления; l a и c – задаваемые целые числа; l x 0 – задается в начале расчета алгоритма. n В результате случайное число:
Генерирование базового распределения Мультипликативный конгруэнтный метод n расчет по формуле: l где mod – операция получения остатка от деления; l a и c – задаваемые целые числа; l x 0 – задается в начале расчета алгоритма. n В результате случайное число:
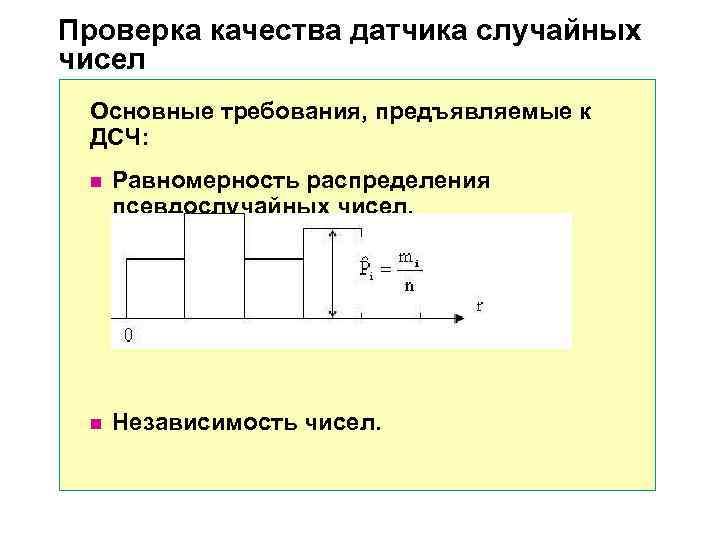
 Проверка качества датчика случайных чисел Основные требования, предъявляемые к ДСЧ: n Равномерность распределения псевдослучайных чисел. n Независимость чисел.
Проверка качества датчика случайных чисел Основные требования, предъявляемые к ДСЧ: n Равномерность распределения псевдослучайных чисел. n Независимость чисел.
 Проверка равномерности распределения n Дисперсия оценки вероятности события при n опытах и биномиальной схеме испытаний n В действительности оценка может отличаться от истинного значения на 3 n Если оценка входит в интервал: то нет основания отвергать гипотезу о равномерности
Проверка равномерности распределения n Дисперсия оценки вероятности события при n опытах и биномиальной схеме испытаний n В действительности оценка может отличаться от истинного значения на 3 n Если оценка входит в интервал: то нет основания отвергать гипотезу о равномерности
 Проверка независимости чисел n Автокорреляционная функция отражает корреляцию между элементами последовательности, расположенными на расстоянии s (s = 0, 1, 2, . . . ). n Корреляционная функция К(s) идеальной псевдослучайной последовательности должна l равняться D[r] при s = 0 l и нулю при s > 0, где r – случайная величина, значениями которой являются числа, генерируемые ДСЧ,
Проверка независимости чисел n Автокорреляционная функция отражает корреляцию между элементами последовательности, расположенными на расстоянии s (s = 0, 1, 2, . . . ). n Корреляционная функция К(s) идеальной псевдослучайной последовательности должна l равняться D[r] при s = 0 l и нулю при s > 0, где r – случайная величина, значениями которой являются числа, генерируемые ДСЧ,
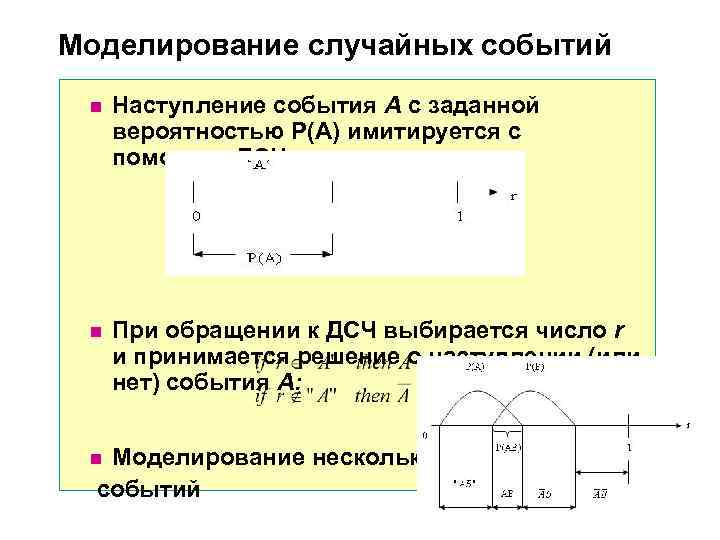
 Моделирование случайных событий n Наступление события А с заданной вероятностью Р(А) имитируется с помощью ДСЧ n При обращении к ДСЧ выбирается число r и принимается решение о наступлении (или нет) события А: n Моделирование нескольких событий
Моделирование случайных событий n Наступление события А с заданной вероятностью Р(А) имитируется с помощью ДСЧ n При обращении к ДСЧ выбирается число r и принимается решение о наступлении (или нет) события А: n Моделирование нескольких событий
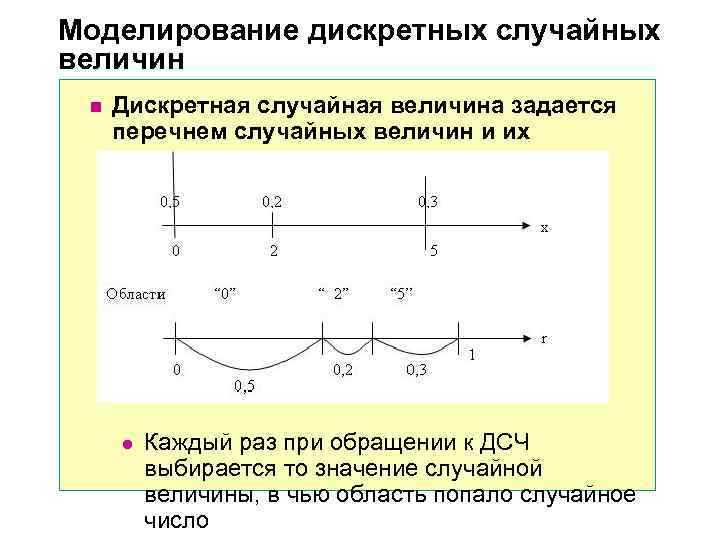
 Моделирование дискретных случайных величин n Дискретная случайная величина задается перечнем случайных величин и их вероятностями l Каждый раз при обращении к ДСЧ выбирается то значение случайной величины, в чью область попало случайное число
Моделирование дискретных случайных величин n Дискретная случайная величина задается перечнем случайных величин и их вероятностями l Каждый раз при обращении к ДСЧ выбирается то значение случайной величины, в чью область попало случайное число
 Лекция 5. Моделирование непрерывных случайных величин с произвольными законами распределения
Лекция 5. Моделирование непрерывных случайных величин с произвольными законами распределения
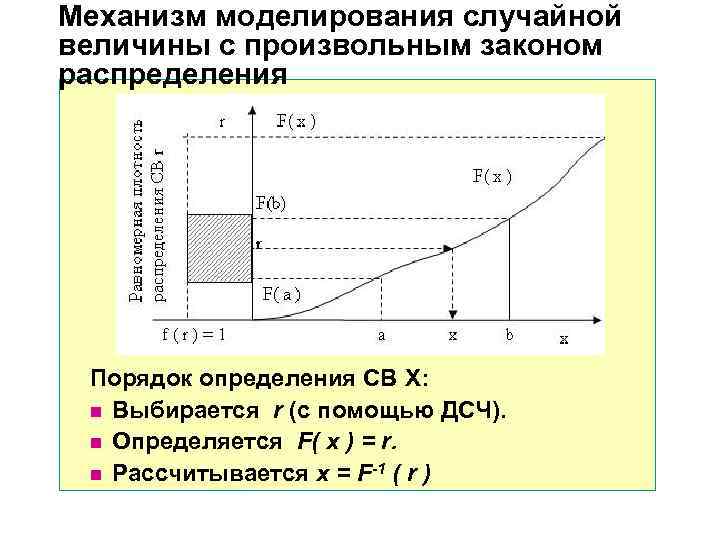
 Механизм моделирования случайной величины с произвольным законом распределения Порядок определения СВ X: n Выбирается r (с помощью ДСЧ). n Определяется F( x ) = r. n Рассчитывается x = F-1 ( r )
Механизм моделирования случайной величины с произвольным законом распределения Порядок определения СВ X: n Выбирается r (с помощью ДСЧ). n Определяется F( x ) = r. n Рассчитывается x = F-1 ( r )
 Моделирование экспоненциального распределения n Функция распределения n Выражение для определения искомой величины:
Моделирование экспоненциального распределения n Функция распределения n Выражение для определения искомой величины:
 Моделирование нормального распределения n Эмпирические формулы: центральная предельная теорема теории вероятностей: n сумма случайных величин имеет распределение асимптотически стремящееся к нормальному, если все СВ имеют конечные математические ожидания и дисперсии и ни одна из величин по своему значению резко не отличается от остальных l СВ с нормальным законом можно получить путем суммирования величин r (для практических задач можно ограничиться 12 ю слагаемыми)
Моделирование нормального распределения n Эмпирические формулы: центральная предельная теорема теории вероятностей: n сумма случайных величин имеет распределение асимптотически стремящееся к нормальному, если все СВ имеют конечные математические ожидания и дисперсии и ни одна из величин по своему значению резко не отличается от остальных l СВ с нормальным законом можно получить путем суммирования величин r (для практических задач можно ограничиться 12 ю слагаемыми)
 Приближенные методы моделирования непрерывных случайных величин Метод численного интегрирования n Для определения x требуется решить уравнение Последовательность действий: n С помощью ДСЧ выбирается r. n Интегрируется f(x) до тех пор, пока интеграл не превзойдет r. n То значение x, при котором F(x) r и есть искомое значение x.
Приближенные методы моделирования непрерывных случайных величин Метод численного интегрирования n Для определения x требуется решить уравнение Последовательность действий: n С помощью ДСЧ выбирается r. n Интегрируется f(x) до тех пор, пока интеграл не превзойдет r. n То значение x, при котором F(x) r и есть искомое значение x.
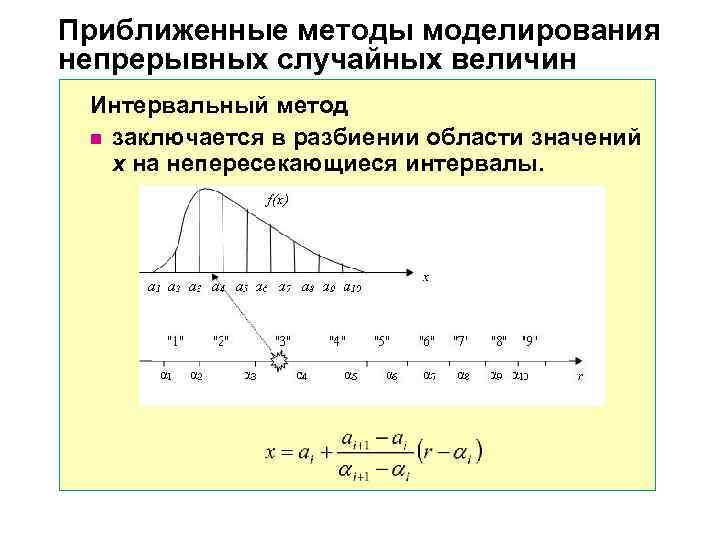
 Приближенные методы моделирования непрерывных случайных величин Интервальный метод n заключается в разбиении области значений х на непересекающиеся интервалы.
Приближенные методы моделирования непрерывных случайных величин Интервальный метод n заключается в разбиении области значений х на непересекающиеся интервалы.
 Лекция 6. Организация компьютерного моделирования инфокоммуникационных систем
Лекция 6. Организация компьютерного моделирования инфокоммуникационных систем
 Моделирование марковских цепей с дискретным временем переходов n Для марковских цепей переходы осуществляются в соответствии с заданными вероятностями l Переход в новое состояние связывается с попаданием СВ r в интервал: если r попал в интервал “j", то переход на шаге (t + 1) произойдет в состояние j. В этом случае переходы будут происходить с частотами, в пределе совпадающими с
Моделирование марковских цепей с дискретным временем переходов n Для марковских цепей переходы осуществляются в соответствии с заданными вероятностями l Переход в новое состояние связывается с попаданием СВ r в интервал: если r попал в интервал “j", то переход на шаге (t + 1) произойдет в состояние j. В этом случае переходы будут происходить с частотами, в пределе совпадающими с
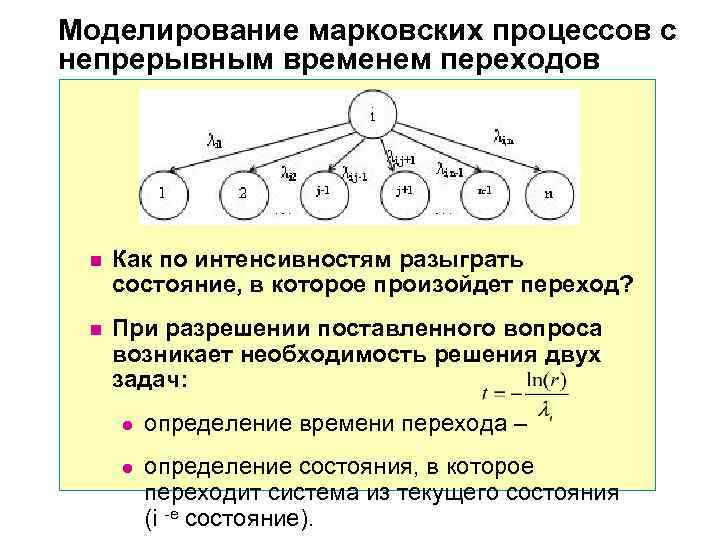
 Моделирование марковских процессов с непрерывным временем переходов n Как по интенсивностям разыграть состояние, в которое произойдет переход? n При разрешении поставленного вопроса возникает необходимость решения двух задач: l определение времени перехода – l определение состояния, в которое переходит система из текущего состояния (i е состояние).
Моделирование марковских процессов с непрерывным временем переходов n Как по интенсивностям разыграть состояние, в которое произойдет переход? n При разрешении поставленного вопроса возникает необходимость решения двух задач: l определение времени перехода – l определение состояния, в которое переходит система из текущего состояния (i е состояние).
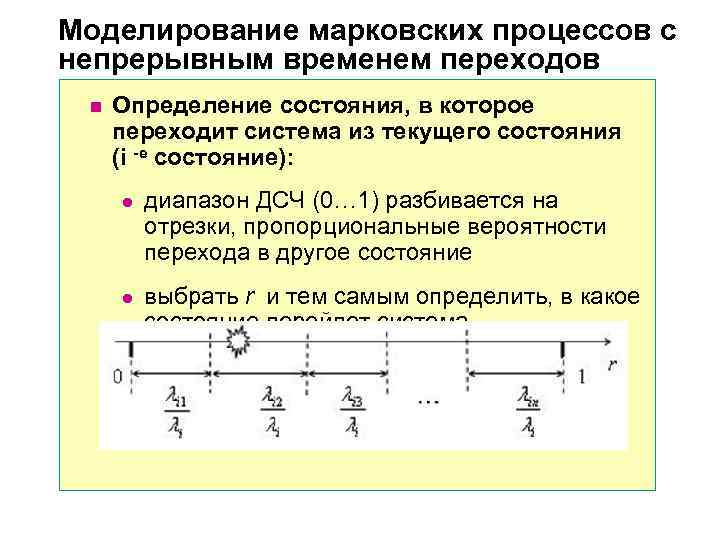
 Моделирование марковских процессов с непрерывным временем переходов n Определение состояния, в которое переходит система из текущего состояния (i е состояние): l диапазон ДСЧ (0… 1) разбивается на отрезки, пропорциональные вероятности перехода в другое состояние l выбрать r и тем самым определить, в какое состояние перейдет система
Моделирование марковских процессов с непрерывным временем переходов n Определение состояния, в которое переходит система из текущего состояния (i е состояние): l диапазон ДСЧ (0… 1) разбивается на отрезки, пропорциональные вероятности перехода в другое состояние l выбрать r и тем самым определить, в какое состояние перейдет система
 Моделирование систем массового обслуживания n Для решения задачи статистического моделирования функциони рования СМО должны быть заданы следующие исходные данные: l описание СМО (тип, параметры, критерии эффективности рабо ты системы); l параметры закона распределения периодичности поступлений требований в систему; l параметры закона распределения времени пребывания требова ния в очереди (для СМО с ожиданием); l параметры закона распределения времени обслуживания требо ваний в системе .
Моделирование систем массового обслуживания n Для решения задачи статистического моделирования функциони рования СМО должны быть заданы следующие исходные данные: l описание СМО (тип, параметры, критерии эффективности рабо ты системы); l параметры закона распределения периодичности поступлений требований в систему; l параметры закона распределения времени пребывания требова ния в очереди (для СМО с ожиданием); l параметры закона распределения времени обслуживания требо ваний в системе .
 Моделирование систем массового обслуживания n Время функционирования системы разделяется на достаточно большое количество подинтервалов l единиц времени, в течение которых не может возникнуть более одной заявки или завершиться выполнение более одной заявки
Моделирование систем массового обслуживания n Время функционирования системы разделяется на достаточно большое количество подинтервалов l единиц времени, в течение которых не может возникнуть более одной заявки или завершиться выполнение более одной заявки
 Моделирование систем массового обслуживания n Для каждого такого подинтервала: l последовательно моделируется факт появления новой заявки (да/нет). l проверяется наличие свободного канала (закончено ли обслуживание какой то заявки) и загрузка его заявкой из очереди, l проверяется наличие мест в очереди с последующим выводом (принять в очередь/отказать в обслуживании) и т. д. l Фиксируется число отказов, время ожидания заявок в очереди и в системе вообще, число заявок в очереди в каждый момент и другие значения.
Моделирование систем массового обслуживания n Для каждого такого подинтервала: l последовательно моделируется факт появления новой заявки (да/нет). l проверяется наличие свободного канала (закончено ли обслуживание какой то заявки) и загрузка его заявкой из очереди, l проверяется наличие мест в очереди с последующим выводом (принять в очередь/отказать в обслуживании) и т. д. l Фиксируется число отказов, время ожидания заявок в очереди и в системе вообще, число заявок в очереди в каждый момент и другие значения.

