Раздел № 1. ТЕЛА ВРАЩЕНИЯ.

Раздел № 1. ТЕЛА ВРАЩЕНИЯ. 1. Определение и основные элементы тел вращения. Площадь поверхности и объем. 2. Практическая работа № 1. 3. Решение задач. 4. Зачет № 1. 5. Контрольная работа № 1.

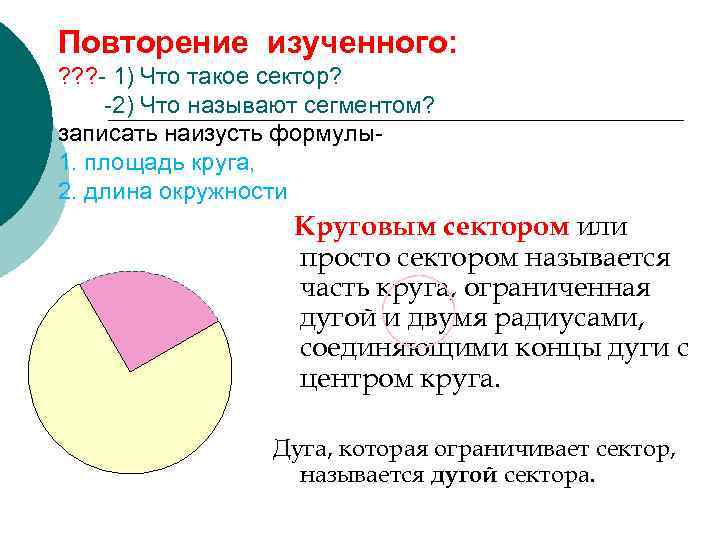
Повторение изученного: ? ? ? - 1) Что такое сектор? -2) Что называют сегментом? записать наизусть формулы- 1. площадь круга, 2. длина окружности Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Дуга, которая ограничивает сектор, называется дугой сектора.

Круговой сегмент Круговым сегментом называется общая часть круга и полуплоскости. Стр. 225

Изучение нового материала. Опр-1. Областью вместе с ее границей называют замкнутой областью. Опр-2. Телом называют конечную замкнутую область. Опр-3. Граница тела называется поверхностью тела. Опр-4. Телом вращения называется такое тело, которое плоскостями, перпендикулярными некоторой прямой (оси вращения), пересекается по кругам с центрами на этой прямой.

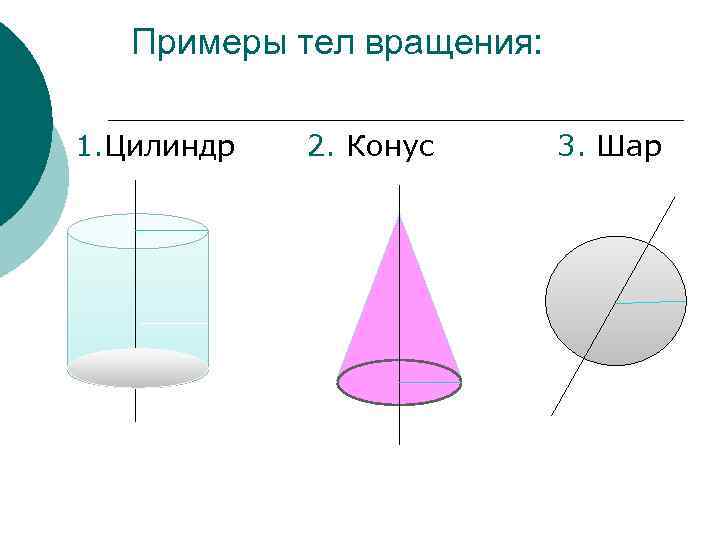
Примеры тел вращения: 1. Цилиндр 2. Конус 3. Шар

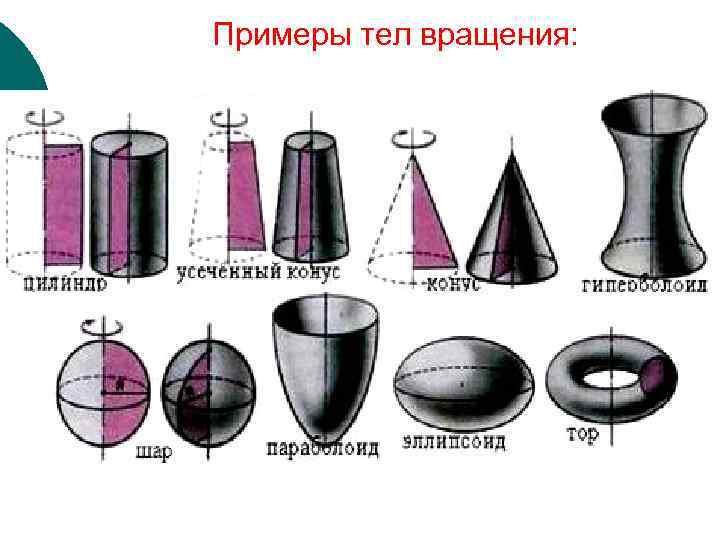
Примеры тел вращения:

Круговой прямой цилиндр

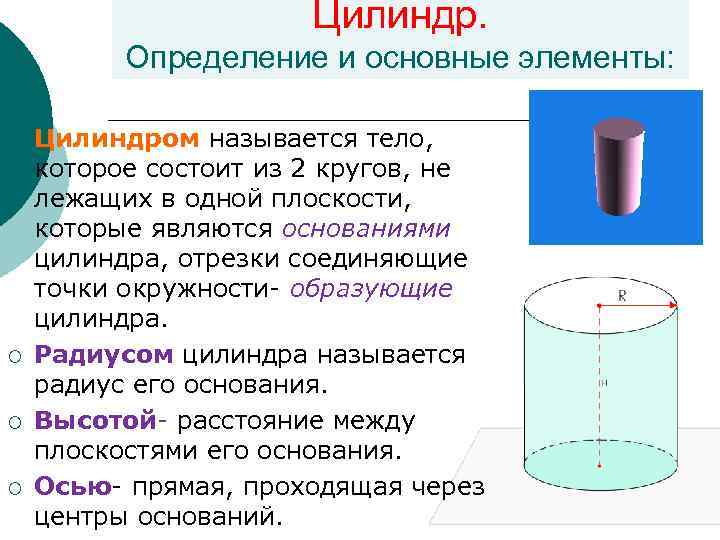
Цилиндр. Определение и основные элементы: ¡ Цилиндром называется тело, которое состоит из 2 кругов, не лежащих в одной плоскости, которые являются основаниями цилиндра, отрезки соединяющие точки окружности- образующие цилиндра. ¡ Радиусом цилиндра называется радиус его основания. ¡ Высотой- расстояние между плоскостями его основания. ¡ Осью- прямая, проходящая через центры оснований.

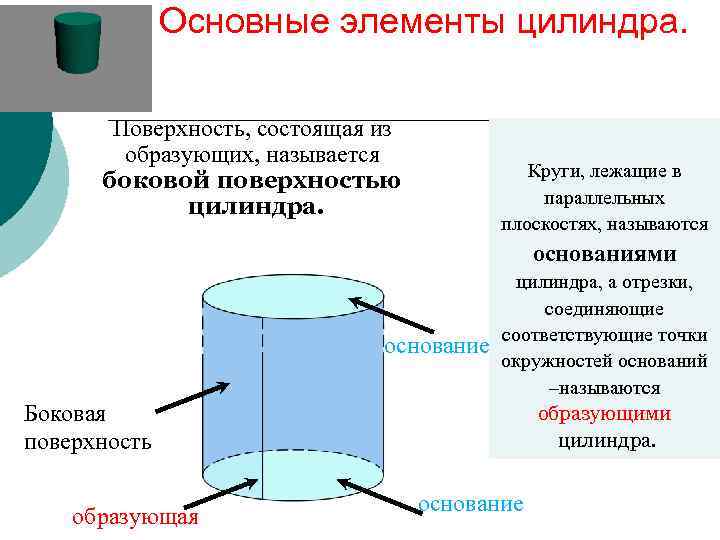
Основные элементы цилиндра. Поверхность, состоящая из образующих, называется Круги, лежащие в боковой поверхностью параллельных цилиндра. плоскостях, называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки основание окружностей оснований –называются Боковая образующими поверхность цилиндра. основание образующая

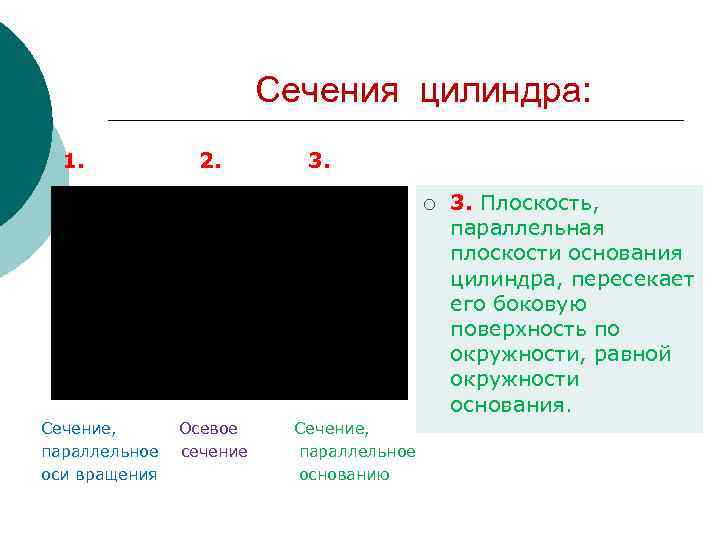
Сечения цилиндра: 1. 2. 3. ¡ 3. Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания. Сечение, Осевое Сечение, параллельное сечение параллельное оси вращения основанию

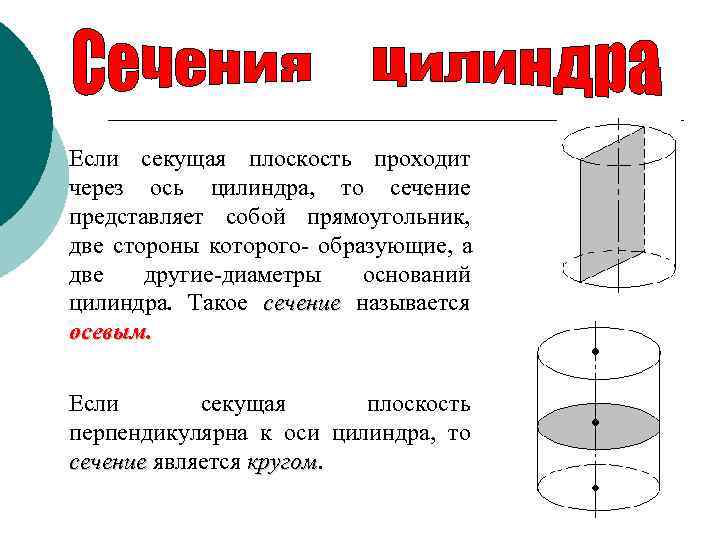
Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого- образующие, а две другие-диаметры оснований цилиндра. Такое сечение называется осевым. Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. кругом

Многогранник, вписанный в цилиндр. ¡ Призмой, вписанной в цилиндр называется такая призма, у которой плоскостями оснований является плоскости цилиндра, а боковыми рёбрами - образующие цилиндра.

Вычисление площади поверхности и объема цилиндра: ¡ Sбок. = 2 Hпr - ПЛОЩАДЬ БОКОВОЙ поверхности ¡ Sцил. = 2 пr(r+h)площадь ПОЛНОЙ ПОВЕРХНОСТИ ¡ V=Sосн. h= пr 2 h - ОБЪЁМ цилиндр. R- радиус H- высота

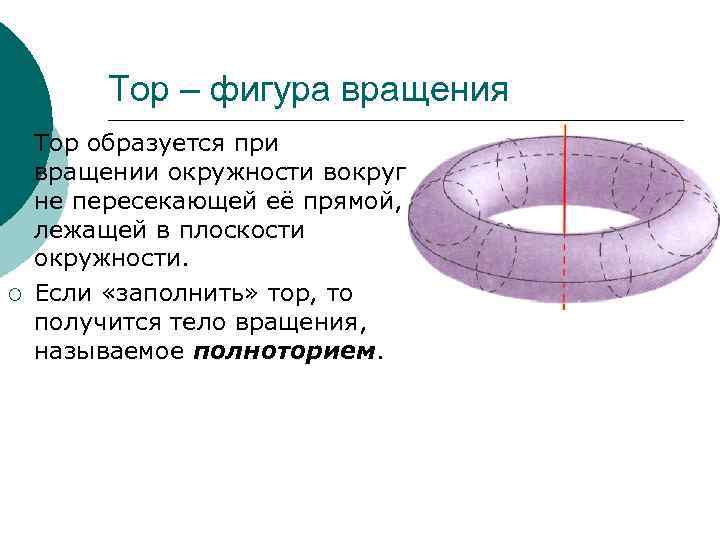
Тор – фигура вращения ¡ Тор образуется при вращении окружности вокруг не пересекающей её прямой, лежащей в плоскости окружности. ¡ Если «заполнить» тор, то получится тело вращения, называемое полноторием.

Объем и площадь поверхности тора Если r – радиус окружности, R – расстояние от её центра до оси, то ¡ V=2πR πr²=2π²Rr²; ¡ Sповерх=4π²Rr.