Продвинутая эк-трика 1.ppt
- Количество слайдов: 29

РАЗДЕЛ 1. ОБОБЩЕННАЯ ЛИНЕЙНАЯ МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ (ОЛММР) И ОБОБЩЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ. 1. 1. МЕСТО ЭКОНОМЕТРИКИ В ЭКОНОМИЧЕСКИХ И МАТЕМАТИКО-СТАТИСТИЧЕСКИХ ДИСЦИПЛИНАХ. 1. 2. ТЕОРЕТИЧЕСКИЕ И ПРИКЛАДНЫЕ АСПЕКТЫ ПОСТРОЕНИЯ ИСХОДНОЙ СИСТЕМЫ СТАТИСТИЧЕСКИХ ДАННЫХ (ИСД). 1. 3. КРАТКИЕ СВЕДЕНИЯ ПО КЛАССИЧЕСКОЙ ЛИНЕЙНОЙ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ (КЛММР). 1. 4. МУЛЬТИКОЛЛИНЕАРНОСТЬ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ И ЕЕ УСТРАНЕНИЕ С ПОМОЩЬЮ МЕТОДА ГЛАВНЫХ КОМПОНЕНТ. 1. 5. ЛИНЕЙНАЯ МОДЕЛЬ РЕГРЕССИИ С ГЕТЕРОСКЕДАСТИЧНЫМИ ОСТАТКАМИ. 1. 6. ОБОБЩЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ. 1. 7. ОЛММР С АВТОКОРРЕЛИРОВАННЫМИ ОСТАТКАМИ.

1. 1. Э К О Н О М Е Т Р И К А МЕТОДЫ: РЕГРЕССИОННЫЙ АНАЛИЗ; АНАЛИЗ ВРМЕНЕННЫХ РЯДОВ; СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ; СТАТИСТИЧЕСКИЕ МЕТОДЫ КЛАССИФИКАЦИ И СНИЖЕНИЯ РАЗМЕРНОСТИ. ЭКОНОМИЧЕСКАЯ ТЕОРИЯ (МАКРО- И МИКРОЭКОНОМИКА, МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА) И С ТО Ч Н И К И БА З О В Ы Х ПРИЛОЖЕНИЯ: М А К Р О У Р О В Е Н Ь (МОДЕЛИ НАЦИОНАЛЬНОЙ ЭКОНОМИКИ); М Е З О У Р О В Е Н Ь (МОДЕЛИ РЕГИОНАЛЬНОЙ ЭКОНОМИКИ, ОТРАСЛЕЙ, СЕКТОРОВ); М И К Р О У Р О В Е Н Ь (МОДЕЛИ ПОВЕДЕНИЯ ПОТРЕБИТЕЛЯ, ДОМАШНИХ ХОЗЯЙСТВ, ФИРМ, ПРЕДПРИЯТИЙ). СОЦИАЛЬНО-ЭКОНОМИЧЕСКАЯ СТАТИСТИКА (ВКЛЮЧАЯ ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЙ) ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ КОМПОНЕНТОВ ЭКОНОМЕТРИЧЕСКОЙ НАУКИ

1. 2. ПРАВОМЕРНО РАССМОТРЕТЬ ДВА ОСНОВОПОЛАГАЮЩИХ ПОДХОДА К ИНТЕРПРЕТАЦИИ И АНАЛИЗУ ИСХОДНОЙ СИСТЕМЫ ДАННЫХ (ИСД). ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА - ПОСТАВЩИК СУЩЕСТВЕННОЙ ЧАСТИ ИСПОЛЬЗУЕМОГО В ЭКОНОМЕТРИКЕ И ПРИКЛАДНОЙ СТАТИСТИКЕ МАТЕМАТИЧЕСКОГО АППАРАТА. В СВОЮ ОЧЕРЕДЬ ЭКОНОМЕТРИКА - ПОСТАВЩИК ПОСТАНОВОК ЗАДАЧ ДЛЯ ПРИКЛАДНОЙ СТАТИСТИКИ. . ПОДХОДЫ К АНАЛИЗУ И ИНТЕРПРЕТАЦИИ ИСД ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИЙ 1. ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ ДВУХ СОВОКУПНОСТЕЙ ОБЪЕКТОВ: А). РЕАЛЬНО НАБЛЮДАЕМОЙ (ВЫБОРКА); Б) ТЕОРЕТИЧЕСКИ ДОМЫСЛИВАЕМОЙ (ГЕНЕРАЛЬНАЯ СОВ-ТЬ). 2. ОСНОВНЫЕ СВОЙСТВА И ХАРАКТЕРИСТИКИ ВЫБОРКИ, ЭМПИРИЧЕСКИМИ (ИЛИ ВЫБОРОЧНЫМИ), МОГУТ БЫТЬ ПРОАНАЛИЗИРОВАНЫ И ВЫЧИСЛЕНЫ ПО ИМЕЮЩИМСЯ СТАТИСТИЧЕСКИМ ДАННЫМ. 3. ОСНОВНЫЕ СВОЙСТВА И ХАРАКТЕРСТИКИ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ НЕ ИЗВЕСТНЫ ИССЛЕДОВАТЕЛЮ, НО ОСНОВНОЕ ПРЕДНАЗНАЧЕНИЕ МАТ. СТАТ. МЕТОДОВ ПОЛУЧЕНИЕ НАИБОЛЕЕ ТОЧНОГО ПРЕДСТАВЛЕНИЯ С ПОМОЩЬЮ ВЫБОРОК. 4. УДАЧНОЕ РЕШЕНИЕ ПРОБЛЕМЫ ИХ ГЕНЕЗИСА, Т. Е. ПРАВИЛЬНЫЙ ВЫБОР ВЕРОЯТНОСТНОЙ МОДЕЛИ МЕХАНИЗМА ГЕНЕРАЦИИ ЭТИХ ДАННЫХ (МОДЕЛИ ЗРВ). ЛОГИКО-АЛГЕБРАИЧЕСКИЙ 1. ИССЛЕДОВАТЕЛЬ НЕ РАСПОЛАГАЕТ НИКАКИМИ АПРИОРНЫМИ СВЕДЕНИЯМИ О ВЕРОЯТНОСТНОЙ ПРИРОДЕ ЭТИХ ДАННЫХ ИЛИ ЭТИ ДАННЫЕ ВООБЩЕ НЕ ИНТЕРПРЕТИРУЮТСЯ КАК ВЫБОРКА ИЗ ГЕНЕРАЛЬНОЙ СОВОК-ТИ. 2. ИССЛЕДОВАТЕЛЬ ВЫНУЖДЕН ОСНОВЫВАТЬСЯ НА ЛОГИКЕ СОДЕРЖАТЕЛЬНОСТИ ДАННЫХ В ВИДЕ КРИТЕРИЯ НЕКОТОРОГО АЛГЕБРАИЧЕСКОГО ТИПА. ДИДЭ Э. И. И ДР. МЕТОДЫ АНАЛИЗА ДАННЫХ: ПОДХОД ОСНОВАННЫЙ НА МЕТОДЕ ДИНАМИЧЕСКИХ СГУЩЕНИЙ. – М. : ФИН. И СТАТ-КА, 1985.

ПОСТРОЕНИЕ ИСД ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ ПРЕДСТАВЛЕНИЕ ИСД В ВИДЕ МАТРИЦЫ (ТАБЛИЦЫ) «ОБЪЕКТ-СВОЙСТВО» . - ЗНАЧЕНИЕ СОСТОЯНИЕ -ГО АНАЛИЗИРУЕМОГО ПРИЗНАКА, ХАРАКТЕРИЗУЮЩЕГО - ГО ОБЪЕКТА В МОМЕНТ ВРЕМЕНИ МОЖНО СКАЗАТЬ, ЧТО ИСД ВИДА (1. 1) СОДЕРЖАТ - РЕАЛИЗАЦИИ -МЕРНОГО ВРЕМЕННОГО РЯДА -КОЛИЧЕСТВЕННАЯ ХАРКТЕРИСТИКА ПОПАРНОГО СРАВНЕНИЯ ДВУХ ОБЪЕТОВ (ИЛИ ПРИЗНАКОВ) СООТВЕТСТВЕННО С НОМЕРАМИ И СООТНЕСЕННАЯ К МОМЕНТУ ВРЕМЕНИ И МЕРУ ИХ СВЯЗИ ИЛИ МОЖЕТ ВЫРАЖАТЬ МЕРУ СХОДСТВА ИЛИ РАЗЛИЧИЯ ОБЪЕКТОВ ВЗАИМОДЕЙСТВИЯ (НАПР. I КВАДРАНТ МОБа, ГЕОМЕТРИЧЕСКОЕ РАССТОЯНИЕ МЕЖДУ ОБЪЕКТАМИ, МЕРУ ВЗАИМНОЙ КОРРЕЛИРОВАННОСТИ (ПРИЗНАКОВ). (1. 2) КВАДРАТНАЯ МАТРИЦА И В ОСН. СИММ-АЯ.

1. 3. РЕЗУЛЬТИРУЮЩАЯ (ЗАВИСИМАЯ, ЭНДОГЕННАЯ ПЕРЕМЕННАЯ); - ОБЪЯСНЯЮЩИЕ (ПРЕДИКТОРНЫЕ, ЭКЗОГЕННЫЕ) ПЕРЕМЕННЫЕ. ФУНКЦИЯ НАЗЫВАЕТСЯ ФУНКЦИЕЙ РЕГРЕССИИ ПО , ЕСЛИ ОНА ОПИСЫВАЕТ ИЗМЕНЕНИЕ УСЛОВНОГО СРЕДНЕГО ЗНАЧЕНИЯ РЕЗУЛЬТИРУЮЩЕЙ ПЕРЕМННОЙ (ПРИ УСЛОВИИ, ЧТО ЗНАЧЕНИЯ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ ЗАФИКСИРОВАНЫ НА ОПРЕДЕЛЕННЫХ УРОВНЯХ). МАТЕМАТИЧЕСКИ ЭТО ОПРЕДЕЛЕНИЕ МОЖЕТ БЫТЬ ЗАПИСАНО В ВИДЕ (1. 3) УРАВНЕНИЕ РЕГРЕССИОННОЙ СВЯЗИ МЕЖДУ И (1. 4) ИСХОДНЫЕ СТАТИСТИЧЕСКИЕ ДАННЫЕ:

КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ (КЛММР) ПРЕДСТАВЛЯЕТ СОБОЙ ПРОСТЕЙШУЮ ВЕРСИЮ КОНКРЕТИЗАЦИИ ТРЕБОВАНИЙ К ОБЩЕМУ ВИДУ ФУНКЦИИ РЕГРЕССИИ ПРИРОДЕ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ И СТАТИСТИЧЕСКИХ РЕГРЕССИОННЫХ ОСТАТКОВ В ОБЩИХ УРАВНЕНИЯХ РЕГРЕССИОННОЙ СВЯЗИ (1. 4). (1. 5) МАТРИЧНАЯ ЗАПИСЬ КЛММР (1. 6) В (1. 6) ИСПОЛЬЗОВАНЫ ОБОЗНАЧЕНИЯ: ,

ВЕКТОР-СТОЛБЕЦ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ; ВЕКТОР-СТОБЕЦ РЕГРЕССИОННЫХ ОСТАТКОВ; НУЛЕВОЙ ВЕКТОР-СТОЛБЕЦ; ЕДИНИЧНАЯ МАТРИЦА; КОВАРИАЦИОННАЯ МАТРИЦА ВЕКТОРА ОСТАТКОВ. МАТРИЦА ЗНАЧЕНИЙ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ ПО НАБЛЮДЕНИЯМ, ВЫСТУПАЮЩИХ КОЭФФИЦИЕНТАМИ ПРИ ОЦЕНИВАЕМЫХ ПАРАМЕТРАХ УРАВНЕНИЯ РЕГРЕССИИ.

ДОПОЛНИТЕЛЬНО К УСЛОВИЯМ (1. 6) ПОСТУЛИРУЮТ НОРМАЛЬНЫЙ ХАРАКТЕР РАСПРЕДЕЛЕНИЯ РЕГРЕССИОННЫХ ОСТАТКОВ И ЗАПИСЫВАЕТСЯ В ВИДЕ ОЦЕНКИ ПАРАМЕТРОВ УРАВНЕНИЯ РЕГРЕССИИ. ОНИ ПОЛУЧАЮТСЯ ИЗ ПОСЛЕДОВАТЕЛЬНОСТИ ПРЕОБРАЗОВАНИЙ: (1. 7)

1. 4. МУЛЬТИКОЛЛИНЕАРНОСТЬ В СТРОГОМ СМЫСЛЕ ОПРЕДЕЛЯЕТСЯ УСЛОВИЕМ НАРУШЕНИЯ ОДНОГО ИЗ ТРЕБОВАНИЙ КЛММР, А ИМЕННО, ТРЕБОВАНИЯ К РАНГУ МАТРИЦЫ (СМ. (1. 6). ЭКЗОГЕНННЫЕ ПЕРЕМЕННЫЕ ХАРАКТЕРИЗУЮТСЯ СВОЙСТВОМ ПОЛНОЙ МУЛЬТИКОЛЛИНЕАРНОСТИ, ЕСЛИ РАНГ МАТРИЦЫ МЕНЬШЕ РЕАЛЬНО МУЛЬТИКОЛЛИНЕАРНОСТЬ ИМЕЕТ МЕСТО В СЛУЧАЯХ СУЩЕСТВОВАНИЯ ДОСТАТОЧНО ТЕСНЫХ СТАТИСТИЧЕСКИХ СВЯЗЕЙ МЕЖДУ ЭКЗОГЕННЫМИ (ОБЪЯСНЯЮЩИМИ) ПЕРЕМЕННЫМИ. ОДНИМ ИЗ МЕТОДОВ ЕЕ УСТРАНЕНИЯ ЯВЛЯЕТСЯ ПЕРЕХОД К ОРТОГОНАЛИЗИРОВАННЫМ ОБЪЯСНЯЮЩИМ ПЕРЕМЕННЫМ С ПОМОЩЬЮ МЕТОДА ГЛАВНЫХ КОМПОНЕНТ. РАССМОТРИМ АЛГОРИТМ РЕАЛИЗАЦИИ ЭТОГО МЕТОДА. ТЕОРЕТИКО-МЕТОДИЧСЕКОЙ ПРЕДПОСЫЛКОЙ ПОСТРОЕНИЯ БАЗЫ ДАННЫХ МОЖЕТ ПОСЛУЖИТЬ МНОГОМЕРНАЯ (ТРЕХМЕРНАЯ) МАТРИЦА ИСХОДНЫХ ДАННЫХ ВИДА (1. 1). ПРЕДСТАВИМ МАТРИЦУ ТАК: ЗНАЧЕНИЕ ОБЪЕКТЕ В МОМЕНТ ВРЕМЕНИ (1. 8) МОЖНО ПЕРЕПИСАТЬ В ВИДЕ ПАНЕЛЬНЫХ ДАННЫХ, МАТРИЦА ДАННЫХ ПРЕОБРАЗУЕТСЯ В ДВУХМЕРНУЮ. СТРОК (НАБЛЮДЕНИЙ) СОСТАВИТЬ ПОКАЗАТЕЛЯ НА ПУСТЬ В РЕЗУЛЬТАТЕ ЧИСЛО А СТОЛБЦЫ БУДУТ ПРЕДСТАВЛЕНЫ ПРИЗНАКАМИ, ЧИСЛО КОТОРЫХ СОСТАВИТ ИТАК, В НОВОМ ПРЕДСТАВЛЕНИИ МАТРИЦА ДАННЫХ ПРИМЕТ ВИД:

ЯВЛЯЕТСЯ МАТРИЦЕЙ РАЗМЕРНОСТИ ЧИСЛЕННОЕ ЗНАЧЕНИЕ ПРИЗНАКА НА ОБЪЕКТЕ НАБЛЮДЕНИЯ. ЗАДАЧИ И МЕТОДЫ МОДЕЛИРОВАНИЯ ЗАВИСИМОСТЕЙ В ПРОСТРАНСТВЕННО-ВРЕМЕННЫХ ВЫБОРКАХ ТЕСНО СВЯЗАНЫ С ОДНОРОДНОСТЬЮ СОВОКУПНОСТИ ОБЪЕКТОВ. ПРИ ЕЕ СОБЛЮДЕНИИ ВОЗМОЖНО ВЫЯВЛЕНИЕ ПОДДАЮЩИХСЯ ЭКОНОМИЧЕСКОМУ ОБЪЯСНЕНИЮ ОБОБЩАЮЩИХ (ЛАТЕНТНЫХ) ФАКТОРОВ. ОДНОРОДНОСТЬ СОВОКУПНОСТИ ОБЪЕКТОВ МОЖЕТ БЫТЬ ПРОВЕРЕНА ПУТЕМ ОЦЕНКИ ЗНАЧИМОСТИ МАТРИЦЫ КОЭФФИЦИЕНТОВ ПАРНОЙ КОРРЕЛЯЦИИ ПРИЗНАКОВ-ПОКАЗАТЕЛЕЙ ПРИ ПОМОЩИ КРИТЕРИЯ УИЛКСА. ГДЕ ЗНАЧИМОСТЬ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ ПОДТВЕРЖДАЕТСЯ, ЕСЛИ НАБЛЮДЕННОЕ ЗНАЧЕНИЕ КРИТЕРИЯ УИЛКСА ТАБЛИЧНОЕ ЗНАЧЕНИЕ РАСПРЕДЕЛЕНИЯ ПРИ ЗАДАННОМ УРОВНЕ ВЕРОЯТНОСТИ ОШИБКИ СВОБОДЫ ГДЕ И ЧИСЛА СТЕПЕНЕЙ В СВОЮ ОЧЕРЕДЬ, МАТРИЦА КОЭФФИЦИЕНТОВ ПАРНОЙ КОРРЕЛЯЦИИ ПРИЗНАКОВ, И ГДЕ СОБСТВЕННЫЕ ЗНАЧЕНИЯ (ЧИСЛА) МАТРИЦЫ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ.

1. 4. 1 СТАНДАРТИЗАЦИЯ ИСХОДНОЙ СИСТЕМЫ ДАННЫХ. ГДЕ И 1. 4. 2 ПОЛУЧЕНИЕ МАТРИЦЫ КОЭФФИЦЕНТОВ ПАРНОЙ КОРРЕЛЯЦИИ ПРИЗНАКОВ: ГДЕ 1. 4. 3 (а) ТРАНСПОНИРОВАННАЯ МАТРИЦА РАЗМЕРНОСТИ ПОЛУЧЕНИЕ ФАКТОРНЫХ ВЕСОВ (ФАКТОРНОЙ МАТРИЦЫ ( ПРОВЕДЕНИЯ РЯДА ПОСЛЕДОВАТЕЛЬНЫХ ДЕЙСТВИЙ. ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ МАТРИЦЫ ) ОСУЩЕСТВЛЯЕТСЯ НА ОСНОВЕ ПО ХАРАКТЕРИСТИЧЕСКОМУ УР-Ю

ВЕЩЕСТВЕННЫЕ ХАРАКТЕРИСТИЧЕСКИЕ КОРНИ УРАВНЕНИЯ (1. 13), И ПРИ ЭТОМ (б) ОПРЕДЕЛЕНИЕ СООТВТЕТСТВУЮЩИХ СОБСТВЕННЫМ ЗНАЧЕНИЯМ МАТРИЦЫ СОБСТВЕННЫХ ВЕКТОРОВ: СОБСТВЕННЫЙ ВЕКТОР МАТРИЦЫ ГДЕ СООТВЕТСТВУЮЩИЙ СОСБСТВЕННОМУ ЗНАЧЕНИЮ ТАКИМ ОБРАЗОМ МОЖЕМ СОСТАВИТЬ МАТРИЦУ ИЗ СОБСТВЕННЫХ ВЕКТОРОВ-СТОЛБЦОВ (в) ОПРЕДЕЛЕНИЕ МАТРИЦЫ ИЗ НОРМИРОВАННЫХ СОБСТВЕННЫХ ВЕКТОРОВ (1. 16) ГДЕ (г) ОПРЕДЕЛЕНИЕ МАТРИЦЫ ФАКТОРНЫХ ВЕСОВ (НАГРУЗОК)

ГДЕ МАТРИЦА ФАКТОРНЫХ НАГРУЗОК ВЕС С ЭЛЕМЕНТАМИ ЯВЛЯЕТСЯ МАТРИЦЕЙ ПОРЯДКА ЧАСТНОГО (ИСХОДНОГО) ПОКАЗАТЕЛЯ (ПРИЗНАКА) В ФОРМИРОВАНИИ ГЛАВНОЙ КОМПОНЕНТЫ. ЯВЛЯЮТСЯ ЧАСТНЫМИ КОЭФФИЦИЕНТАМИ КОРЕЛЯЦИИ, ОТРАЖАЮЩИМИ СВЯЗЬ ИСХОДНЫХ ПОКАЗАТЕЛЕЙ ДЛЯ КАЖДОГО И ГЛАВНЫХ КОМПОНЕНТ СТОЛБЦА МАТРИЦЫ СОБСТВЕННОЕ ЗНАЧЕНИЕ МАТРИЦЫ Т. О. В ОБЩЕЙ ДИСПЕРСИИ ВСЕХ СЛЕДОВАТЕЛЬНО, СПРАВЕДЛИВО УСЛОВИЕ: ЯВЛЯЕТСЯ ДИСПЕРСИЕЙ ГЛАВНОЙ КОМПОНЕНТЫ ИСХОДНЫХ ПОКАЗАТЕЛЕЙ, ОПРЕДЕЛЯЮЩИХ СКРЫТУЮ (ЛАТЕНТНУЮ) ЗАКОНОМЕРНОСТЬ, ОТРАЖАЕМОЙ ГЛАВНОЙ КОМПОНЕНТОЙ ОБЩЕЙ ДИСПЕРСИИ ВСЕХ ИСХОДНЫХ ПОКАЗАТЕЛЕЙ В СВОЮ ОЧЕРЕДЬ, ОБЪЯСНЯЕМОЙ ПОСЛЕДНЯЯ ОБЪЯСНЯЕТ (РИС. 1. 1). СООТВЕТСТВУЕТ ВЕЛИЧИНЕ ДИСПЕРСИИ ИСХОДНОГО ГЛАВНОЙ КОМПОНЕНТОЙ. ПОКАЗАТЕЛЯ,
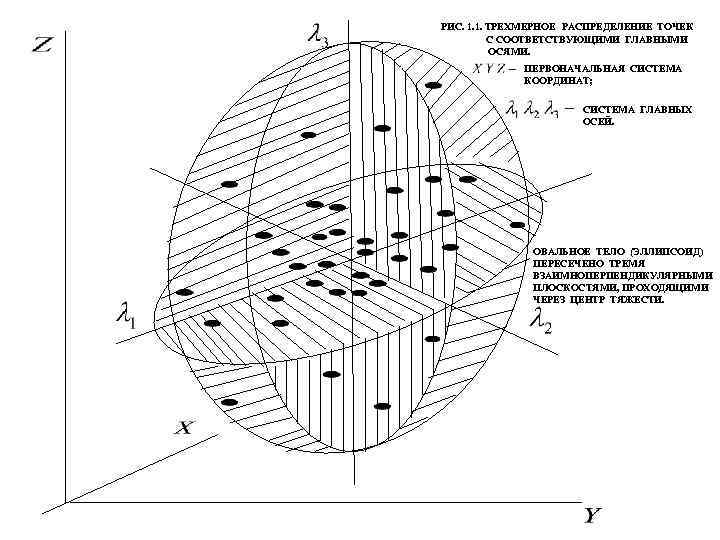
РИС. 1. 1. ТРЕХМЕРНОЕ РАСПРЕДЕЛЕНИЕ ТОЧЕК С СООТВЕТСТВУЮЩИМИ ГЛАВНЫМИ ОСЯМИ. ПЕРВОНАЧАЛЬНАЯ СИСТЕМА КООРДИНАТ; СИСТЕМА ГЛАВНЫХ ОСЕЙ. ОВАЛЬНОЕ ТЕЛО (ЭЛЛИПСОИД) ПЕРЕСЕЧЕНО ТРЕМЯ ВЗАИМНОПЕРПЕНДИКУЛЯРНЫМИ ПЛОСКОСТЯМИ, ПРОХОДЯЩИМИ ЧЕРЕЗ ЦЕНТР ТЯЖЕСТИ.
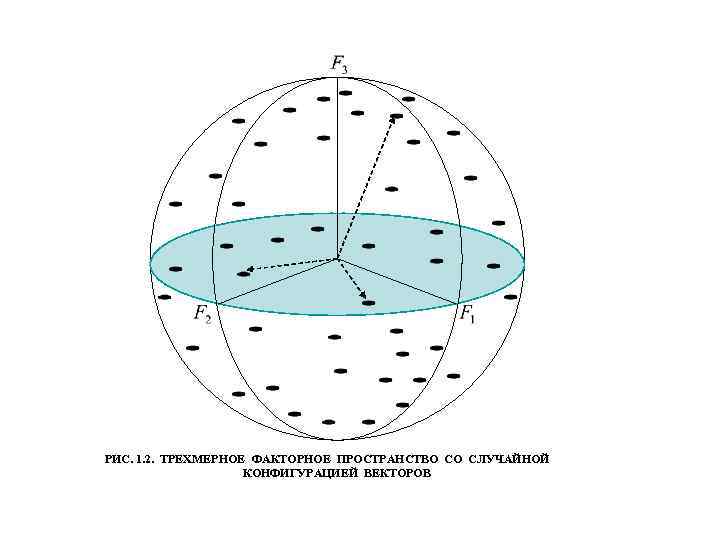
РИС. 1. 2. ТРЕХМЕРНОЕ ФАКТОРНОЕ ПРОСТРАНСТВО СО СЛУЧАЙНОЙ КОНФИГУРАЦИЕЙ ВЕКТОРОВ
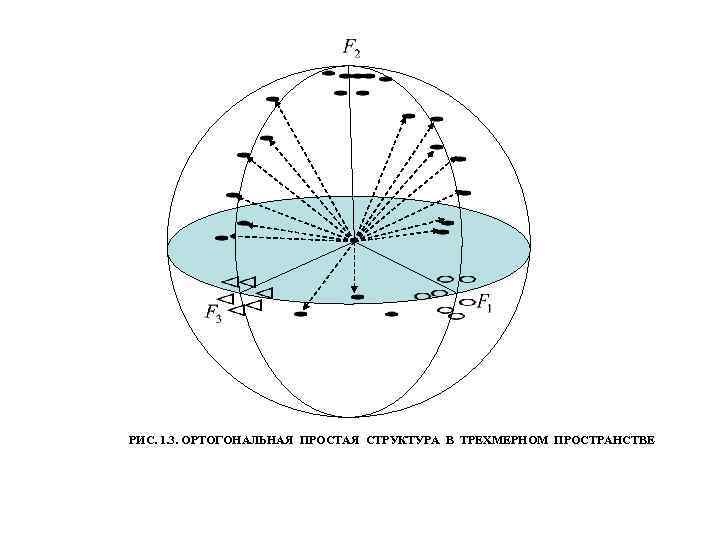
РИС. 1. 3. ОРТОГОНАЛЬНАЯ ПРОСТАЯ СТРУКТУРА В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ

ОБЕСПЕЧЕНИЕ ПОЛУЧЕНИЯ ПОДДАЮЩИХСЯ ИНТЕРПРЕТАЦИИ ЗНАЧЕНИЙ ФАКТОРНЫХ НАГРУЗОК С ЦЕЛЬЮ СОДЕРЖАТЕЛЬНОГО ЭКОНОМИЧЕСКОГО ОБЪЯСНЕНИЯ ГЛАВНЫХ КОМПОНЕНТ ОСУЩЕСТВЛЯЕТСЯ ВРАЩЕНИЕМ ФАКТОРНОЙ МАТРИЦЫ. НЕ ВСЕ ГЛАВНЫЕ КОМПОНЕНТЫ МОГУТ БЫТЬ ИСПОЛЬЗОВАНЫ ДЛЯ ЭКОНОМИЧЕСКИ ДОСТУПНОЙ ИНТЕРПРЕТАЦИИ ВЫЯВЛЕННЫХ СКРЫТЫХ ЗАКОНОМЕРНОСТЕЙ. ЦЕЛЕСООБРАЗНО ОТОБРАТЬ ТАКОЕ КОЛИЧЕСТВО ГЛАВНЫХ КОМПОНЕНТ, КОТОРОЕ ОБЪЯСНЯЕТ НЕ МЕНЕЕ 75% СУММАРНОЙ ДИСПЕРСИИ. КРИТЕРИАЛЬНОЙ ОСНОВОЙ ВЫБОРА СЛУЖАТ ВЕЛИЧИНЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ ИСХОДНЫХ ПОКАЗАТЕЛЕЙ. ВЫБОР ОСУЩЕСТВЛЯЕТСЯ ПО ТЕМ ДЛЯ КОТОРЫХ ФАКТОРНЫЕ НАГРУЗКИ МОГУТ ОТЛИЧАТЬСЯ РАВНОМЕРНЫМ РАСПРЕДЕЛЕНИЕМ ИХ ЗНАЧЕНИЙ (РИС. 1. 2), ЧТО ЗАТРУДНЯЕТ ЭКОНОМИЧЕСКУЮ ИНТЕРПРЕТАЦИЮ ГЛАВНОЙ КОМПОНЕНТЫ ГЕОМЕТРИЧЕСКИ, КАК ВИДНО ИЗ РИС. 1. 2, ЭТО СООТВЕТСТВУЕТ ТАКОЙ СИТУАЦИИ, КОГДА В ПРОСТРАНСТВЕ КООРДИНАТЫ ВЕКТОРА РАВНОУДАЛЕНЫ ОТ ОСЕЙ. ЭКОНОМИЧЕСКИ ИНТЕРПРЕТИРУЕМО ТАКОЕ РАСПОЛОЖЕНИЕ КООРДИНАТ (ЗНАЧЕНИЙ ФАКТОРНЫХ НАГРУЗОК), КОГДА БОЛЬШАЯ ИХ ЧАСТЬ ПРИЛЕГАЕТ К КООРДИНАТНЫМ ОСЯМ, Т. Е. ЗНАЧЕНИЯ ПАРАМЕТРОВ РАВНЫ НУЛЮ ИЛИ БЛИЗКИ К НЕМУ, А НЕБОЛЬШАЯ ЧАСТЬ ОСТАВШИХСЯ ФАКТОРНЫХ НАГРУЗОК ИМЕЕТ БЛИЗКИЕ ПО МОДУЛЮ К ЕДИНИЦЕ ЗНАЧЕНИЯ. . ДЛЯ ДОСТИЖЕНИЯ ТАКОГО РАСПОЛОЖЕНИЯ ФАКТОРНЫХ ОСЕЙ ПРОИЗВОДИТСЯ ИХ ВРАЩЕНИЕ В ОРТОГОНАЛЬНОМ ПРОСТРАНСТВЕ ВЕКТОРОВ (ГЛАВНЫХ КОМПОНЕНТ) (РИС. 1. 3). ИСПОЛЬЗУЮТСЯ РАЗЛИЧНЫЕ КРИТЕРИИ ВРАЩЕНИЯ, МНОГИЕ ИЗ КОТОРЫХ РЕАЛИЗОВАНЫ В ПРИКЛАДНЫХ ПРОГРАММНЫХ ПРОДУКТАХ ПО ЭКОНОМЕТРИКЕ И МНОГОМЕРНОЙ СТАТИСТИКЕ. НАПРИМЕР, ВАРИМАКС, КВАРТИМАКС, ОБЛИМИН И ДР.

ОПРЕДЕЛЕНИЕ ЧИСЛЕННЫХ ЗНАЧЕНИЙ ГЛАВНЫХ КОМПОНЕНТ ОСУЩЕСТВЛЯЕТСЯ ПО ВСЕМ ОЦЕНКИ ЭЛЕМЕНТОВ ГЛАВНЫХ КОМПОНЕНТ СООТВЕТСТВУЮТ КООРДИНАТАМ ВЕКТОРОВ ФАКТОРНЫЙ ВЕС ОБЪЕКТА НАБЛЮДЕНИЯ В ГЛАВНОЙ КОМПОНЕНТЕ. МАТРИЦА СОСТАВЛЕННАЯ ИЗ ВЕКТОРОВ Т. Е. И СОВПАДАЮЩАЯ ПО РАЗМЕРНОСТИ С МАТРИЦЕЙ ИСХОДНЫХ ДАННЫХ (1. 9), ОПРЕДЕЛЯЕТСЯ ПО ФОРМУЛЕ: В ДАЛЬНЕЙШЕМ МАТРИЦУ ЦЕЛЕСООБРАЗНО ПРЕДСТАВИТЬ В ТРАНСПОНИРОВАННОМ ВИДЕ, ТАК КАК ПО СВОЕЙ РАЗМЕРНОСТИ ОНА БУДЕТ СОВПАДАТЬ С ИСХОДНОЙ МАТРИЦЕЙ ДАННЫХ МАТРИЦА ЧИСЛЕННЫХ ЗНАЧЕНИЙ ГЛАВНЫХ КОМПОНЕНТ ПОЗВОЛЯЕТ ПОЛУЧИТЬ УРАВНЕНИЕ РЕГРЕССИИ НА ГЛАВНЫХ КОМПОНЕНТАХ. В ЧАСТНОСТИ, ПРИ НАЛИЧИИ ВЫБОРКИ ПО КАКОМУ-НИБУДЬ АНАЛИЗИРУЕМОМУ ПОКАЗАТЕЛЮ (ВЫБОРКА ИМЕЕТСЯ ПО ТЕМ ЖЕ ОБЪЕКТАМ ОТДЕЛЬНО, ЛИБО ПРИСУТСТВУЕТ В ИСХОДНОЙ СИСТЕМЕ ДАННЫХ) МОЖНО ПОСТРОИТЬ УРАВНЕНИЕ ЛИНЕЙНОЙ РЕГРЕССИИ:

ОБОБЩЕННАЯ ЛИНЕЙНАЯ МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ (ОЛММР) ОПИСЫВАЕТСЯ СИСТЕМОЙ СЛЕДУЮЩИХ СООТНОШЕНИЙ И УСЛОВИЙ: ФОРМАЛЬНАЯ ЗАПИСЬ ОЛММР ОТЛИЧАЕТСЯ ОТ КЛММР ТОЛЬКО ОТКАЗОМ ОТ ТРЕБОВАНИЯ НЕКОРРЕЛИРОВАННОСТИ И ГОМОСКЕДАСТИЧНОСТИ ОСТАТКОВ. БУДЕМ ПРЕДПОЛАГАТЬ, ЧТО МАТРИЦА ИЗВЕСТНА, А НЕИЗЫВЕСТНО. ДЛЯ ОЛММР ПРИ ОЦЕНКЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ ИСПОЛЬЗУЕТСЯ ОБОБШЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (ОМНК). В КЧЕСТВЕ ПРИМЕРА РАССМОТРИМ ПРОЦЕДУРУ ЕГО ИСПОЛЬЗОВАНИЯ ДЛЯ КОРРЕКТИРОВКИ ГЕТЕРОСКЕДАСТИЧНОСТИ.

1. 5. ПРИ МОДЕЛИРОВАНИИ МНОГИХ РЕАЛЬНЫХ ЭКОНОМИЧЕСКИХ ИЛИ СОЦИАЛЬНО-ЭКОНОМИЧЕКСИХ ПРОЦЕССОВ ВОЗНИКАЮТ СИТУАЦИИ, КОГДА УСЛОВИЯ КЛММР (1. 6) ОКАЗЫВАЮТСЯ НАРУШЕННЫМИ. ЕСЛИ В КАЧЕСТВЕ ИСХОДНЫХ ДАННЫХ ИСПОЛЬЗУЮТСЯ ВРЕМЕННЫЕ ИЛИ ПРОСТРАНСТВЕННОВРЕМЕННЫЕ ВЫБОРКИ (СМ. ФОРМУЛЫ (1. 1)-(1. 2)), ТО ЧРЕЗМЕРНО ОГРАНИЧИТЕЛЬНЫМ, НЕРЕАЛИСТИЧНЫМ СТАНОВИТСЯ, КАК ПРАВИЛО, УСЛОВИЕ ВЗАИМНОЙ НЕКОРРЕЛИРОВАННОСТИ И ГОМОСКЕДАСТИЧНОСТИ РЕГРЕССИОННЫХ ОСТАТКОВ, КОТОРОЕ В ТЕРМИНАХ КОВАРИАЦИОННОЙ МАТРИЦЫ ОСТАТКОВ ВЫРАЖАЕТСЯ В (1. 6) СООТНОШЕНИЕМ ДАЖЕ ПРИ СОБЛЮДЕНИИ УСЛОВИЯ ВЗАИМНОЙ НЕКОРРЕЛИРОВАННОСТИ ОСТАТКОВ ПРИХОДИТСЯ ЧАСТО АНАЛИЗИРОВАТЬ РЕГРЕССИОННЫЕ МОДЕЛИ, В КОТОРЫХ РАЗБРОС ОСТАТКОВ ОКОЛО ЛИНИИ РЕГРЕССИИ НЕ ОСТАЕТСЯ ПОСТОЯННЫМ (ИМЕЕТ МЕСТО ГЕТЕРОСКЕДАСТИЧНОСТЬ), А МЕНЯЕТСЯ, НАПРИМЕР, ВОЗРАСТАЯ ПРОПОРЦИОНАЛЬНО ЗНАЧЕНИЯМ ФУНКЦИИ РЕГРЕССИИ.

ПРИМЕНЕНИЕ ОМНК ПРЕДПОЛАГАЕТ ПРЕОБРАЗОВАНИЕ ИСХОДНЫХ ДАННЫХ, К КОТОРЫМ ТЕПЕРЬ УЖЕ БУДЕТ ПРИМЕНЯТЬЯСЯ МНК. ИТАК, СРЕДНЕ ЗНАЧЕНИЕ ОСТАТКОВ РАВНО НУЛЮ, А ИХ ДИСПЕРСИЯ ПРОПОРЦИОНАЛЬНА ВЕЛИЧИНЕ ИЛИ СПРАВЕДЛИВО СООТНОШЕНИЕ ДИСПЕРСИЯ ОШИБКИ ПРИ КОНКРЕТНОМ ЗНАЧЕНИИ ФАКТОРА; ПОСТОЯННАЯ ДИСПЕРСИЯ ОШИБКИ ПРИ СОБЛЮДЕНИИ ПРЕДПОСЫЛКИ О ГОМОСКЕДАСТИЧНОСТИ ОСТАТКОВ; КОЭФФИЦИЕНТ ПРОПОРЦИОНАЛЬНОСТИ, МЕНЯЮЩИЙСЯ С ИМЗЕНЕНИЕМ ВЕЛИЧИНЫ ФАКТОРА, ЧТО И ОБУСЛОВЛИВАЕТ НЕООДНОРОДНОСТЬ ДИСПЕРСИИ. ПРЕДПОЛАГАЕТСЯ, ЧТО НЕИЗВЕСТНА, А В ОТНОШЕНИИ ВЕЛИЧИНЫ ВЫДВИГАЮТСЯ ГИПОТЕЗЫ, ХАРАКТЕРИЗУЮЩИЕ СТРУКТУРУ ГЕТЕРОСКЕДАСТИЧНОСТИ. 1. 6. ПРИМЕР. РАССМОТРИМ УРАВНЕНИЕ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ С ГЕТЕРОСКЕДАСТИЧНЫМИ И НЕКОРРЕЛИРОВАННЫМИ ОСТАТКАМИ. ТОГДА МОДЕЛЬ ПРИМЕТ ВИД:

В ПОЛУЧЕННОЙ МОДЕЛИ ОСТАТОЧНЫЕ ВЕЛИЧИНЫ ГЕТЕРОСКЕДАСТИЧНЫ. ПРЕДПОЛОЖИВ В НИХ ОТСУТСТВИЕ АВТОКОРРЕЛЯЦИИ, ПЕРЕЙДЕМ К УРАВНЕНИЮ С ГОМОСКЕДАСТИЧНЫМИ ОСТАТКАМИ, ПОДЕЛИВ ВСЕ ПЕРЕМЕННЫЕ, ЗАФИКСИРОВАННЫЕ В ХОДЕ НАБЛЮДЕНИЯ, . НА В ТАКОМ СЛУЧАЕ ДИСПЕРСИЯ ОСТАТКОВ БУДЕТ ВЕЛИЧИНОЙ ПОСТОЯННОЙ, Т. Е. ДРУГИМИ СЛОВАМИ ОТ РЕГРЕССИИ ПЕРЕМЕННЫХ И ПО МЫ ПЕРЕЙДЕМ К РЕГРЕССИИ НА НОВЫХ ПОЛУЧИВ ПРИ ЭТОМ УРАВНЕНИЕ РЕГРЕССИИ ВИДА: ОЦЕНКА ПАРАМЕТРОВ УРАВНЕНИЯ РЕГРЕССИИ С ПРЕОБРАЗОВАННЫМИ ПЕРЕМЕННЫМИ ДАЕТСЯ С ПОМОЩЬЮ ВЗВЕШЕННОГО МНК, МИНИМИЗИРУЯ СУММУ СИСТЕМА НОРМАЛЬНЫХ УРАВНЕНИЙ ПРИОБРЕТЕТ ВИД:

ДЛЯ ОЛММР, ЗАДАВАЕМОЙ СООТНОШЕНИЯМИ (1. 23), МАТРИЧНАЯ ЗАПИСЬ ОЦЕНОК ПАРАМЕТРОВ ВЕКТОРА-СТОЛБЦА ПО ОБОБЩЕННОМУ МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ ВЫГЛЯДИТ ТАК: (1. 30) МОЖНО ДОКАЗАТЬ, ЧТО В КЛАССЕ ЛИНЕЙНЫХ НЕСМЕЩЕННЫХ ОЦЕНОК ПАРАМЕТРОВ МОДЕЛИ (1. 23) ОЦЕНКИ , ОПРЕДЕЛЕННЫЕ СООТНОШЕНИЯМИ (1. 30), ЯВЛЯЮТСЯ ОПТИМАЛЬНЫМИ В СМЫСЛЕ ТЕОРЕМЫ ГАУССА-МАРКОВА. В СООТВЕТСТВИИ С (1. 23) МЫ СЧИТАЛИ, ЧТО МАТРИЦА ИЗВЕСТНА. С ПРИКЛАДНОЙ ТОЧКИ ЗРЕНИЯ ЭТО ПРЕДПОЛОЖЕНИЕ В БОЛЬШИНСТВЕ СЛУЧАЕВ НЕРЕАЛИСТИЧНО. МАТРИЧНЫЕ ПРЕОБРАЗОВАНИЯ ИСХОДНЫХ ДАННЫХ, ПОДОБНО ПРЕОБРАЗОВАНИЯМ ПО РАССМОТРЕННОМУ ВЫШЕ ПРИМЕРУ ПАРНОЙ ЛИНЕОЙНОЙ РЕГРЕССИИ, СВЯЗАНЫ С ФОРМИРОВАНИЕМ МАТРИЦЫ. ВОЗМОЖЕН СЛЕДУЮЩИЙ ПОДХОД. СУЩЕСТВУЕТ ТАКАЯ НЕВЫРОЖДЕННАЯ ОРТОГОНАЛЬНАЯ МАТРИЦА , ЧТО (1. 31) ТОГДА СЛЕДУЕТ ЗАМЕТИТЬ, ЧТО (1. 32) (1. 33) ВОЗВРАЩАЯСЬ К ОЛММР (1. 23) И, ДОМНОЖИВ ВСЕ ЧЛЕНЫ ПЕРВОГО СООТНОШЕНИЯ СЛЕВА НА ПОЛУЧИМ: (1. 34) ГДЕ (1. 35) ,

ДЛЯ ОЛММР С ГЕТЕРОСКЕДАСТИЧНЫМИ И НЕАВТОКОРРЕЛИРОВАННЫМИ ОСТАТКАМИ МОЖНО УКАЗАТЬ НА ОДИН ИЗ КОНКРЕТНЫХ ВИДОВ МАТРИЦЫ ВСПОМОГАТЕЛЬНОГО ПРЕОБРАЗОВАНИЯ (1. 35). (1. 36) НЕТРУДНО ПРОВЕРИТЬ, ЧТО В ЭТОМ СЛУЧАЕ ВЫПОЛНЯЮТСЯ СООТНОШЕНИЯ (1. 31), (1. 32) И (1. 33). ПРИСТУПАЯ К АНАЛИЗУ ОЛММР, ИССЛЕДОВАТЕЛЬ ДОЛЖЕН, ВО-ПЕРВЫХ, ОТВЕТИТЬ НА ВСЕ ВОПРОСЫ, СВЯЗАННЫЕ СО СПЕЦИФИКАЦИЕЙ МОДЕЛИ, И, ВО-ВТОРЫХ, НАЙТИ ПУТИ К ОПРЕДЕЛЕНИЮ КОВАРИАЦИОННОЙ МАТРИЦЫ ОСТАТКОВ (ЛИБО НА ОСНОВЕ АПРИОРНЫХ ТЕОРЕТИЧЕСКИХ СВЕДЕНИЙ, ЧТО БЫВАЕТ ДОСТАТОЧНО РЕДКО, ЛИБО С ПОМОЩЬЮ НЕКТОРЫХ СПЕЦИАЛЬНЫХ СПОСОБОВ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ НА БАЗЕ ИСХОДНЫХ ДАННЫХ ). ПОСКОЛЬКУ В НАШЕМ СЛУЧАЕ СПЕЦИФИКАЦИЕЙ МОДЕЛИ ВЫБРАНО УРАВНЕНИЕ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ, ОСТАЮТСЯ ТОЛЬКО ВОПРОСЫ, КАСАЮЩИЕЙСЯ ВЕРОЯТНОСТНОЙ ПРИРОДЫ РЕГРЕССИОННЫХ ОСТАТКОВ. ЭТО ЗНАЧИТ, ЧТО, МЫ ДОЛЖНЫ СТАТИСТИЧЕСКИ ПРОВЕРИТЬ, НАХОДИМСЯ ЛИ МЫ, ДЕЙСТВИЕТЛЬНО, В УСЛОВИЯХ ГЕТЕРОСКЕДАСТИЧНОСТИ ОСТАТКОВ. ПРОВЕРКА ГИПОТЕЗ О ГОМО-/ГЕТЕРО-СКЕДАСТИЧНОСТИ РЕГРЕССИОННЫХ ОСТАТКОВ. ПРОВЕРЯЕТСЯ ГИПОТЕЗА (1. 37) ПРИ АЛЬТЕРНАТИВЕ, СОСТОЯЩЕЙ В ТОМ, ЧТО ОСТАТКИ ДАЛЕЕ ОПИШЕМ НЕКОТОРЫЕ ИЗ МЕТОДОВ ПРОВЕРКИ ГИПОТЕЗ. ГЕТЕРОСКЕДАСТИЧНЫ.

1) СЛУЧАЙ ГРУППИРОВАНИЯ ДАННЫХ И БОЛЬШИХ ВЫБОРОК. ПРЕДПОЛАГАЕТСЯ, ЧТО ОБЪЕМ ИМЕЮЩИХСЯ ДАННЫХ ДОСТАТОЧНО ВЕЛИК, И В ЧАСТНОСТИ, ВЫБОРКА МОЖЕТ БЫТЬ РАЗБИТА НА ОПРЕДЕЛЕННОЕ КОЛИЧЕСТВО ПОДВЫБОРОК ОБЪЕМОВ, СООТВЕТСТВЕННО ТАКИМ ОБРАЗОМ, ЧТО ВНУТРИ КАЖДОЙ ИЗ ПОДВЫБОРОК ЗНАЧЕНИЯ ОБЪЯСНЯЮЩИХ ПЕРМЕННЫХ ЛИБО СОВПАДАЮТ ЛИБО НАХОДЯТСЯ В ОДНОМ ИНТЕРВАЛЕ ГРУППИРОВАНИЯ. ПРОВЕРКА ГИПОТЕЗЫ (1. 37) СВОДИТСЯ К ПОСТРОЕНИЮ СТАТИСТИЧЕСКОГО КРИТЕРИЯ ПРОВЕРКИ ГИПОТЕЗЫ ОБ ОДНОРОДНОСТИ ДИСПЕРСИЙ (1. 38) ПО ВЕЛИЧИНАМ СООТВЕТСТВУЮЩИХ ВЫБОРОЧНЫХ ДИСПЕРСИЙ ГДЕ А ЗНАЧЕНИЕ РЕЗУЛЬТИРУЮЩЕЙ ПЕРЕМЕННОЙ В НАБЛЮДЕНИИ ПОДВЫБОРКИ, В КАЧЕСТВЕ ТАКОГО КРИТЕРИЯ МОЖЕТ БЫТЬ ИСПОЛЬЗОВАН, НАПРИМЕР, КРИТЕРИИ БАРТЛЕТА. В СЛУЧАЕ ОТКЛОНЕНИЯ ГИПОТЕЗЫ (1. 38) ЗНАЧЕНИЯ МОГУТ БЫТЬ ИСПОЛЬЗОВАНЫ ДЛЯ КОМПЛЕКТАЦИИ ОЦЕНКИ МАТРИЦЫ В КАЧЕСТВЕ ЕЕ ДИАГОНАЛЬНЫХ ЭЛЕМЕНТОВ. 2) КРИТЕРИЙ ГЛЕЙСЕРА (ГЛЕЙЗЕРА). РАССМАТРИВАЕТСЯ РЕГРЕССИЯ АБСОЛЮТНЫХ ВЕЛИЧИН ОСТАТКОВ ПО НЕОТОРОЙ ФУНКЦИИ ОТ , ГДЕ ЭТО ТА ОБЪЯСНЯЮЩАЯ ПЕРЕМЕННАЯ, ОТ КОТОРОЙ

ГИПОТЕТИЧЕСКИ ЗАВИСИТ УСЛОВНАЯ ДИСПЕРСИЯ ОСТАТКОВ РАССМАТРИВАЮТСЯ ПРОСТЫЕ ФУНКЦИИ ОТ НАПРИМЕР: НА ПРАКТИКЕ (1. 39) (1. 40) (1. 41) РЕШЕНИЕ О ГОМОСКЕДАСТИЧНОСТИ РЕГРЕССИОННЫХ ОСТАТКОВ ПРИНИМАЕТСЯ НА ОСНОВЕ ПРОВЕРКИ МНК-ОЦЕНОК КОЭФФИЦИЕНТОВ НА СТАТИСТИЧЕСКИ ЗНАЧИМОЕ ОТЛИЧИЕ ОТ НУЛЯ. ПРЕИМУЩЕСТВО ЭТОГО ПОДХОДА СОСТОИТ В ТОМ, ЧТО В СЛУЧАЕ ОТКЛОНЕНИЯ ГИПОТЕЗЫ ИССЛЕДОВАТЕЛЬ ОДНОВРЕМЕННО ПОЛУЧАЕТ ОСНОВАНИЕ К ВЫБОРУ ФОРМЫ ПАРАМЕТРИЗАЦИИ. СЛУЧАЙ СТАТИСТИЧЕСКИ ЗНАЧИМЫХ КОЭФФИЦИЕНТОВ В СХЕМЕ (1. 39) СООТВЕТСТВУЕТ ПРЕДПОЛОЖЕНИЮ ГДЕ ВСПОМОГАТЕЛЬНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ИМЕЮТ НУЛЕВЫЕ СРЕДНИЕ ЗНАЧЕНИЯ И ПОСТОЯНННЫЕ ДИСПЕРСИИ. ТОГДА ОЦЕНКА ЗНАЧЕНИЯ ДИАГОНАЛЬНОГО ЭЛЕМЕНТА МАТРИЦЫ (Т. Е. ВЕЛИЧИНЫ В ОБОЗНАЧЕНИЯХ (1. 36) ОПРЕДЕЛИТСЯ СООТНОШЕНИЕМ (1. 42) СЛЕДУЕТ ЗАМЕТИТЬ, ЧТО РЕГРЕССИЯ МОЖЕТ СТРОИТСЯ НЕ ПО ОДНОЙ ОБЪСНЯЮЩЕЙ ПЕРЕМЕННОЙ, А ПО НЕСКОЛЬКИМ ИЛИ ПО ОПРЕДЕЛЕННОЙ КОМБИНАЦИИ ВСЕХ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ. НАПРИМЕР, ПО

1. 7. В РАМКАХ ДАННОГО ПУНКТА МЫ РАССМАТРИВАЕМ МОДЕЛЬ ЛИНЕЙНОЙ РЕГРЕССИИ, В КОТОРОЙ РЕГЕРССИОННЫЕ ОТАТКИ СВЯЗАНЫ АВТОКОРРЕЛЯЦИОННОЙ ЗАВИСИМОСТЬЮ 1 -ГО ПОРЯДКА. ТАКАЯ ЗАВИСИМОСТЬ ОПИСЫВАЕТСЯ СООТНОШЕНИЯМИ (1. 43) ГДЕ НЕКОТОРОЕ ЧИСЛО, ПО АБСОЛЮТНОЙ ВЕЛИЧИНЕ МЕНЬШЕЕ ЕДИНИЦЫ (Т. Е. ), А СЛУЧАЙНЫЕ ВЕЛИЧИНЫ УДОВЛЕТВОРЯЮТ ТРЕБОВАНИЯМ, ПРЕДЪЯВЛЯЕМЫМ К РЕГРЕССИОННЫМ ОСТАТКАМ КЛАССИЧЕСКОЙ МОДЕЛИ, Т. Е. (1. 44) ПРИНИМАЯ ВО ВНИМАНИЕ (1. 43) И (1. 44) , ОПРЕДЕЛИМ ОСНОВНЫЕ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ВЕКТОРА РЕГРЕССИОННЫХ ОСТАТКОВ (СРЕДНИЕ ЗНАЧЕНИЯ И КОВАРИАЦИОННУЮ МАТРИЦУ ). ИЗ (1. 43) СЛЕДУЕТ (1. 45) ИЗ (1. 45) С УЧЕТОМ (1. 44) НЕПОСРЕДСТВЕННО СЛЕДУЕТ: (1. 46)

ДЛЯ ВЫЧИСЛЕНИЯ КОВАРИАЦИИ С УЧЕТОМ СООТНОШЕНИЯ (1. 45) В ВИДЕ: ТОГДА, ПОСКОЛЬКУ ИЗ ВЗАИМНОЙ НЕКОРРЕЛИРОВАННОСТИ НЕКОРРЕЛИРОВАННОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН ПРЕДСТАВИМ ПРОИЗВЕДЕНИЕ СЛЕДУЕТ ВЗАИМНАЯ И ПОЛУЧАЕМ: (1. 47) ГДЕ ДИСПЕРСИЯ ОПРЕДЕЛЕНА СООТНОШЕНИЕМ (1. 46). АВТОКОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТЬ ПЕРВОГО ПОРЯДКА (1. 43), С ПОМОЩЬЮ КОТОРОЙ БЫЛИ СВЯЗАНЫ МЕЖДУ СОБОЙ ОСТАТКИ В СООТВЕТСТВИИ С ОЛММР, ЧЕРЕЗ КОВАРИАЦИИ ЭТИХ ОСТАТКОВ ЭКВИВАЛЕНТНА СООТНОШЕНИЯМ (1. 46)-(1. 47). В РЕЗУЛЬТАТЕ ОЛММР С АВТОКОРРЕЛИРОВАННЫМИ ОСТАТКАМИ В МАТРИЧНОЙ ЗАПИСИ ПРИОБРЕТЕТ ВИД: (1. 48)

ПАРАМЕТР , ВВЕДЕННЫЙ В (1. 43) ПРЕДСТАВЛЯЕТ СОБОЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ МЕЖДУ РЕГРЕССИОННЫМИ ОСТАТКАМИ, ОТСТОЯЩИМИ ДРУГ ОТ ДРУГА ПО ВРЕМЕНИ НА Т. Е. ЕДИНИЦ, (1. 49) КАК ЭТО УЖЕ БЫЛО ОТМЕЧЕНО В П. 1. 6, ОБЩИЙ ПРИЕМ, С ПОМОЩЬЮ КОТОРОГО ОБОБЩЕННАЯ МОДЕЛЬ РЕГРЕССИИ СВОДИТСЯ К КЛАССИЧЕСКОЙ, ЗАКЛЮЧАЕТСЯ ВО ВРЕМЕННОМ ПЕРЕХОДЕ К ПРЕОБРАЗОВАННЫМ ИСХОДНЫМ ДАННЫМ С ПОМОЩЬЮ НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ОБРАЗОМ ПОДОБРАННОЙ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ. ДЛЯ МОДЕЛИ С АВТОКОРРЕЛИРОВАННЫМИ ОСТАТКАМИ В КАЧЕСТВЕ ТАКОЙ МАТРИЦЫ МОЖЕТ БЫТЬ ИСПОЛЬЗОВАНА МАТРИЦА (1. 50) К ПРЕОБРАЗОВАННЫМ ИСХОДНЫМ ДАННЫМ МОЖНО ПРИМЕНИТЬ ПРОЦЕДУРУ ОЦЕНИВАНИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МОДЕЛИ ПО ОБЫЧНОМУ МНК.
Продвинутая эк-трика 1.ppt