РАЗДЕЛ 1 Начертательная геометрия ЛЕКЦИЯ 4

РАЗДЕЛ № 1 «Начертательная геометрия» ЛЕКЦИЯ № 4 ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ, ПРЯМОЙ И ПЛОСКОСТИ

СОДЕРЖАНИЕ: v ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ v ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ

Пересечение прямой с плоскостью В результате пересечения прямой с плоскостью образуется точка, одновременно принадлежащая заданной прямой и плоскости. Эту точку и необходимо построить. При пересечении прямой с плоскостью возможны различные варианты расположения геометрических образов относительно плоскостей проекций. Рассмотрим случай, когда и прямая, и плоскость занимают общее положение.

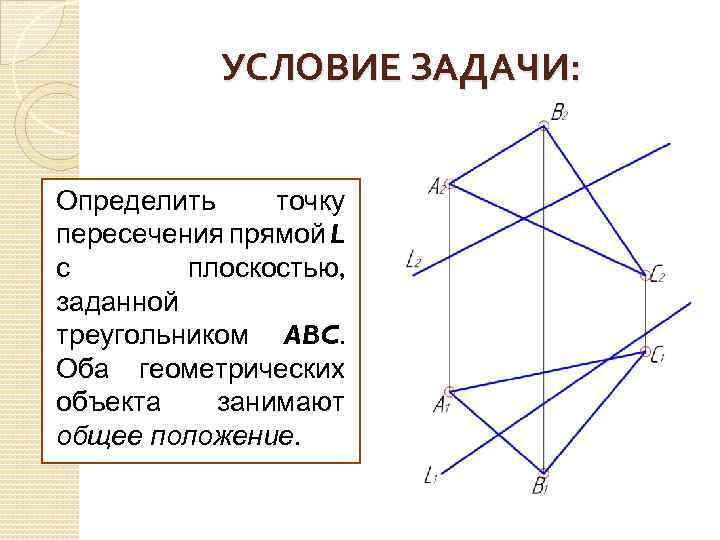УСЛОВИЕ ЗАДАЧИ: Определить точку пересечения прямой L с плоскостью, заданной треугольником ABC. Оба геометрических объекта занимают общее положение.

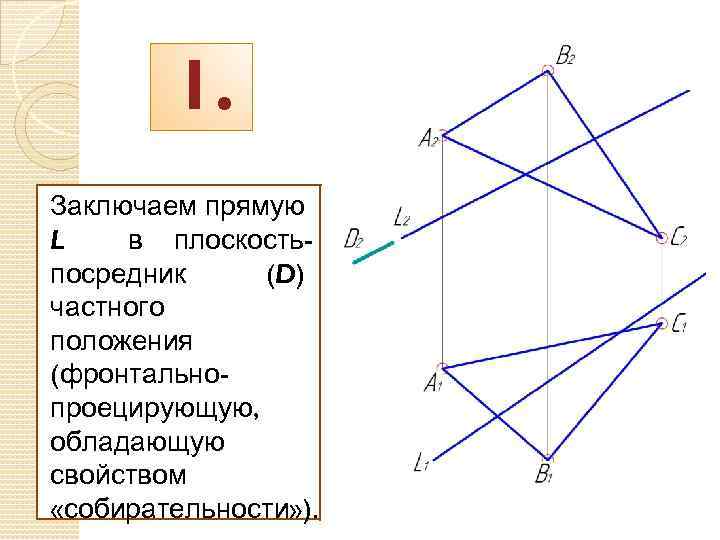1. Заключаем прямую L в плоскостьпосредник (D) частного положения (фронтальнопроецирующую, обладающую свойством «собирательности» ).

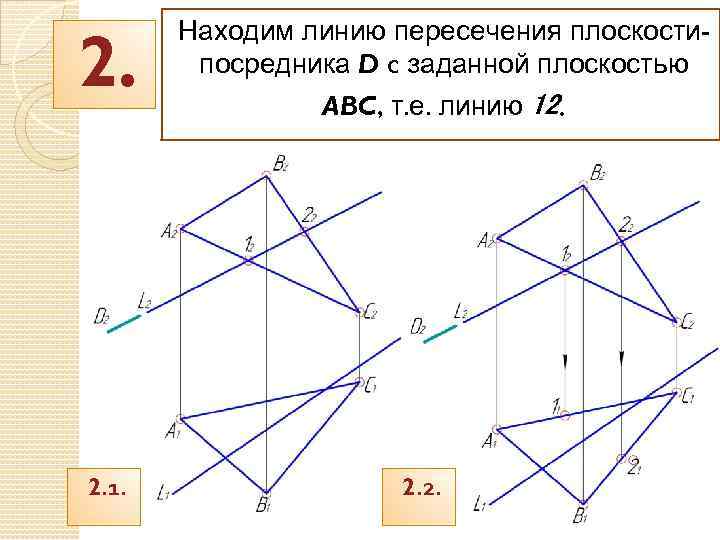2. 2. 1. Находим линию пересечения плоскостипосредника D c заданной плоскостью ABC, т. е. линию 12. 2. 2.

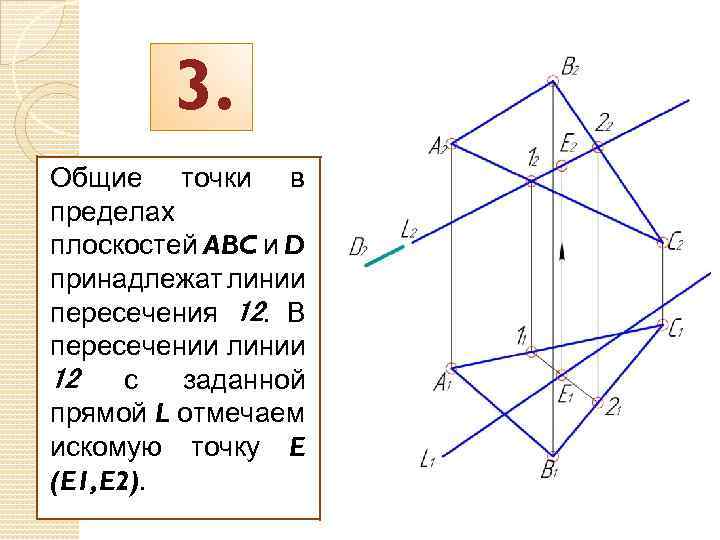3. Общие точки в пределах плоскостей ABC и D принадлежат линии пересечения 12. В пересечении линии 12 с заданной прямой L отмечаем искомую точку E (E 1, E 2).

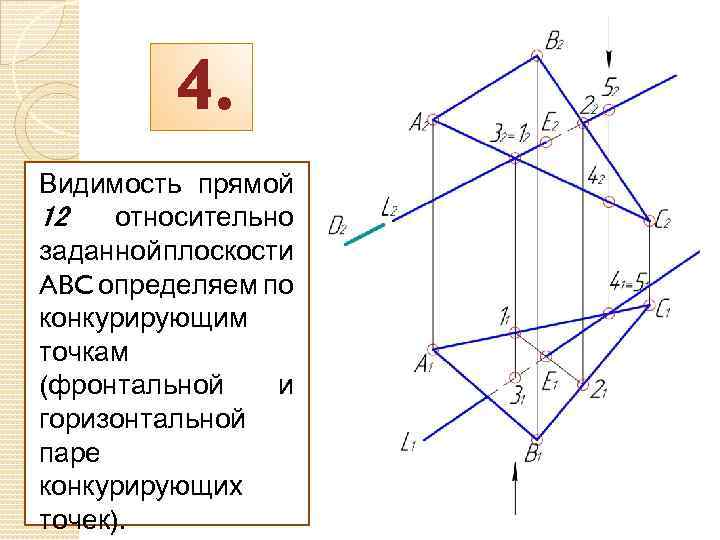4. Видимость прямой 12 относительно заданной плоскости ABC определяем по конкурирующим точкам (фронтальной и горизонтальной паре конкурирующих точек).

Пересечение плоскостей В результате пересечения двух плоскостей образуется прямая линия, которая одновременно принадлежит и одной, и другой заданным плоскостям. Известно, что определением прямой линии являются две точки, которые и необходимо определить. При пересечении плоскостей возможны разные варианты расположения их относительно плоскостей проекций. Рассмотрим случай, когда обе плоскости занимают общее положение.

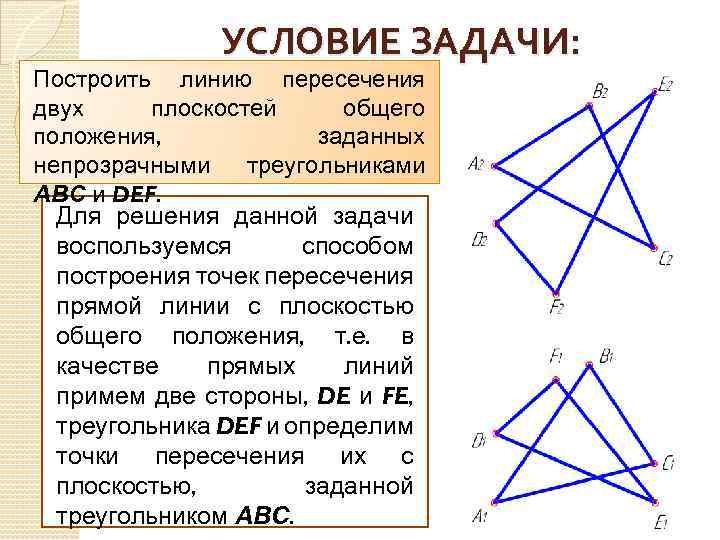УСЛОВИЕ ЗАДАЧИ: Построить линию пересечения двух плоскостей общего положения, заданных непрозрачными треугольниками АВС и DEF. Для решения данной задачи воспользуемся способом построения точек пересечения прямой линии с плоскостью общего положения, т. е. в качестве прямых линий примем две стороны, DE и FE, треугольника DEF и определим точки пересечения их с плоскостью, заданной треугольником АВС.

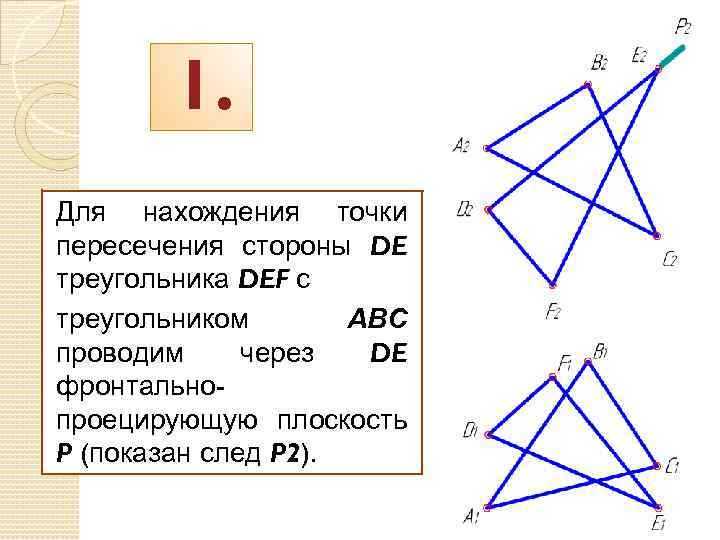1. Для нахождения точки пересечения стороны DE треугольника DEF с треугольником АВС проводим через DE фронтальнопроецирующую плоскость P (показан след P 2).

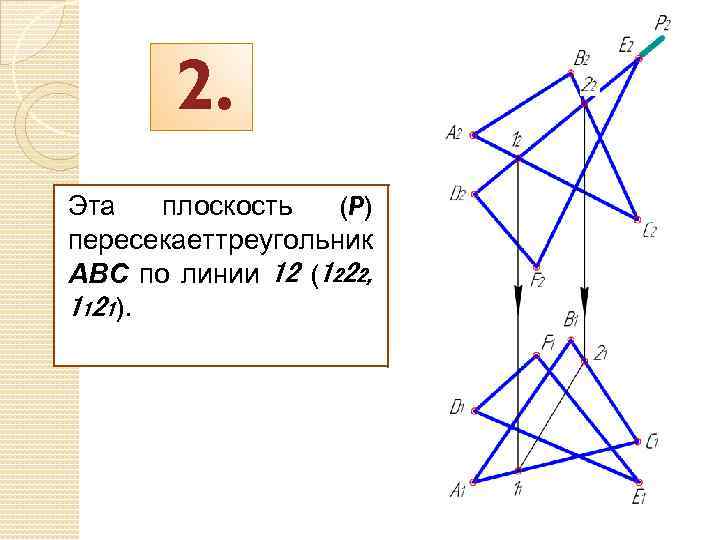2. Эта плоскость (P) пересекаеттреугольник АВС по линии 12 (1222, 1121).

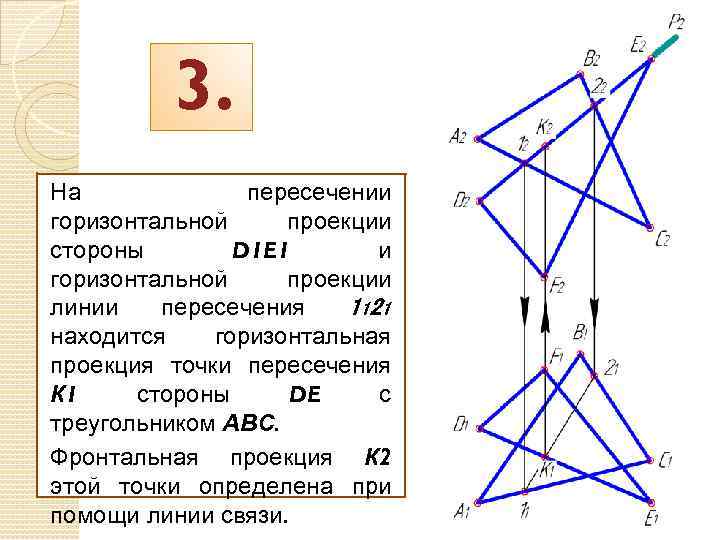3. На пересечении горизонтальной проекции стороны D 1 E 1 и горизонтальной проекции линии пересечения 1121 находится горизонтальная проекция точки пересечения К 1 стороны DE с треугольником АВС. Фронтальная проекция К 2 этой точки определена при помощи линии связи.

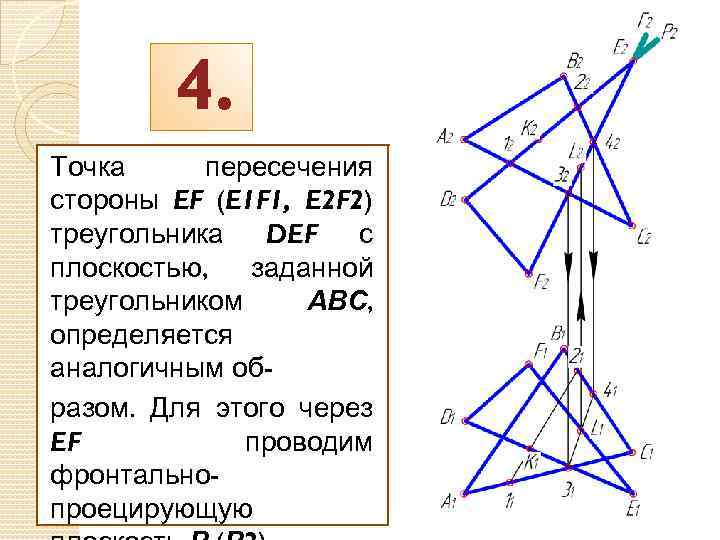4. Точка пересечения стороны EF (E 1 F 1, E 2 F 2) треугольника DEF с плоскостью, заданной треугольником АВС, определяется аналогичным образом. Для этого через EF проводим фронтальнопроецирующую

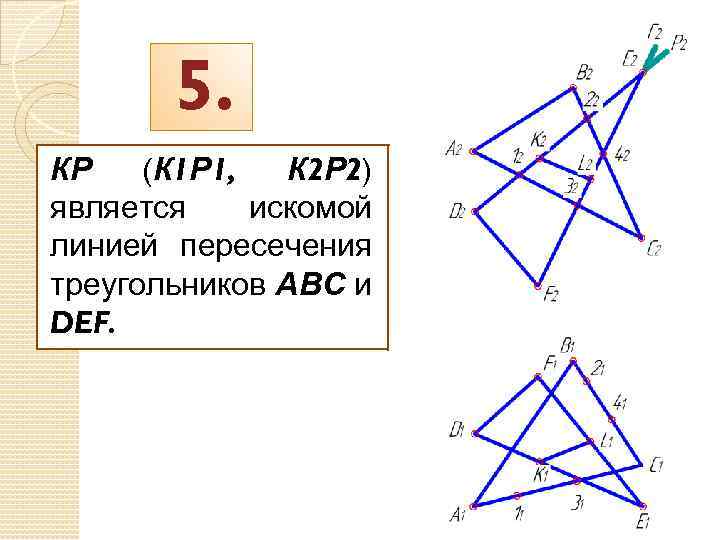5. КР (К 1 Р 1, К 2 Р 2) является искомой линией пересечения треугольников АВС и DEF.

6. В заключение необходимо определить видимые и невидимые участки заданных плоскостей, считая, что треугольники АВС и DEF являются непрозрачным. Видимость плоскостей определяем с помощью конкурирующих точек (фронтальной и горизонтальной пары конкурирующих точек).

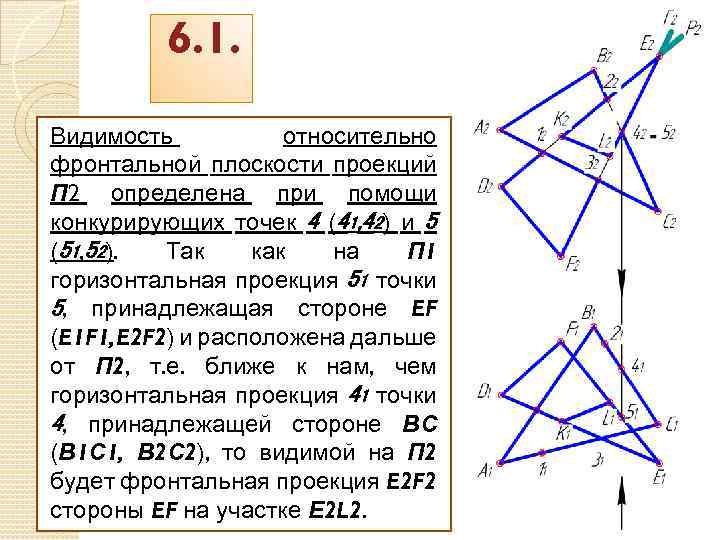6. 1. Видимость относительно фронтальной плоскости проекций П 2 определена при помощи конкурирующих точек 4 (41, 42) и 5 (51, 52). Так как на П 1 горизонтальная проекция 51 точки 5, принадлежащая стороне EF (E 1 F 1, E 2 F 2) и расположена дальше от П 2, т. е. ближе к нам, чем горизонтальная проекция 41 точки 4, принадлежащей стороне ВС (В 1 С 1, В 2 С 2), то видимой на П 2 будет фронтальная проекция E 2 F 2 стороны EF на участке Е 2 L 2.

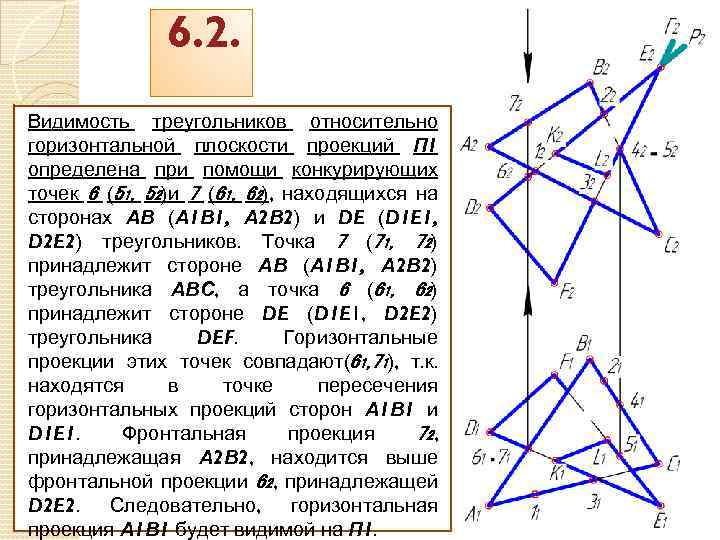6. 2. Видимость треугольников относительно горизонтальной плоскости проекций П 1 определена при помощи конкурирующих точек 6 (51, 52)и 7 (61, 62), находящихся на сторонах АВ (А 1 В 1, А 2 В 2) и DE (D 1 E 1, D 2 E 2) треугольников. Точка 7 (71, 72) принадлежит стороне АВ (А 1 В 1, А 2 В 2) треугольника АВС, а точка 6 (61, 62) принадлежит стороне DE (D 1 E 1, D 2 E 2) треугольника DEF. Горизонтальные проекции этих точек совпадают(61, 71), т. к. находятся в точке пересечения горизонтальных проекций сторон А 1 В 1 и D 1 E 1. Фронтальная проекция 72, принадлежащая А 2 В 2, находится выше фронтальной проекции 62, принадлежащей D 2 E 2. Следовательно, горизонтальная проекция А 1 В 1 будет видимой на П 1.

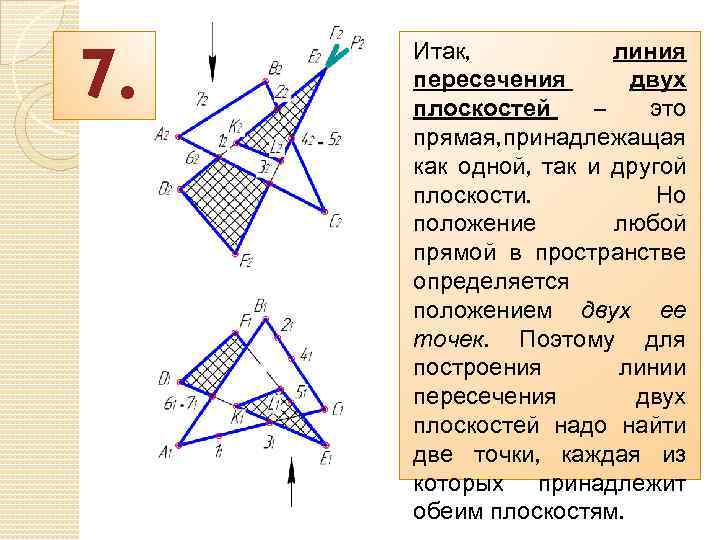7. Итак, линия пересечения двух плоскостей – это прямая, принадлежащая как одной, так и другой плоскости. Но положение любой прямой в пространстве определяется положением двух ее точек. Поэтому для построения линии пересечения двух плоскостей надо найти две точки, каждая из которых принадлежит обеим плоскостям.