 РАЗДЕЛ № 1 «Начертательная геометрия» ЛЕКЦИЯ № 1 МЕТОД ПРОЕКЦИЙ
РАЗДЕЛ № 1 «Начертательная геометрия» ЛЕКЦИЯ № 1 МЕТОД ПРОЕКЦИЙ
 СОДЕРЖАНИЕ: v ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ v ПАРАЛЛЕЛЬНОЙ ПРОЕЦИРОВАНИЕ v ПРОЕКЦИИ ТОЧКИ
СОДЕРЖАНИЕ: v ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ v ПАРАЛЛЕЛЬНОЙ ПРОЕЦИРОВАНИЕ v ПРОЕКЦИИ ТОЧКИ
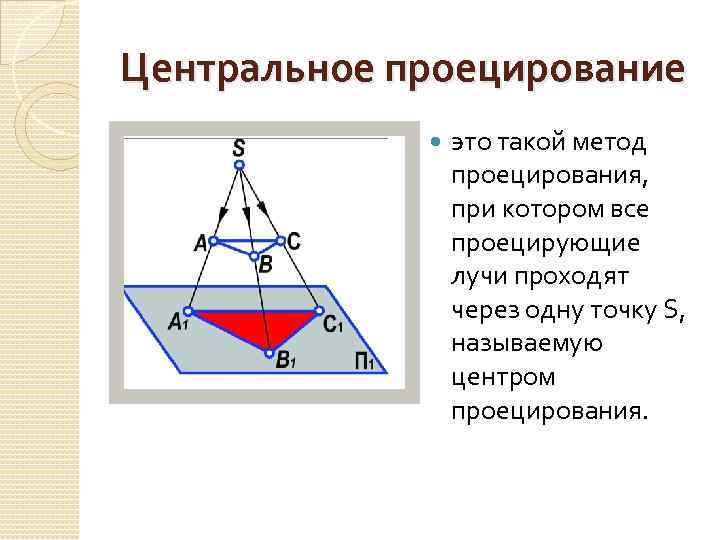 Центральное проецирование это такой метод проецирования, при котором все проецирующие лучи проходят через одну точку S, называемую центром проецирования.
Центральное проецирование это такой метод проецирования, при котором все проецирующие лучи проходят через одну точку S, называемую центром проецирования.
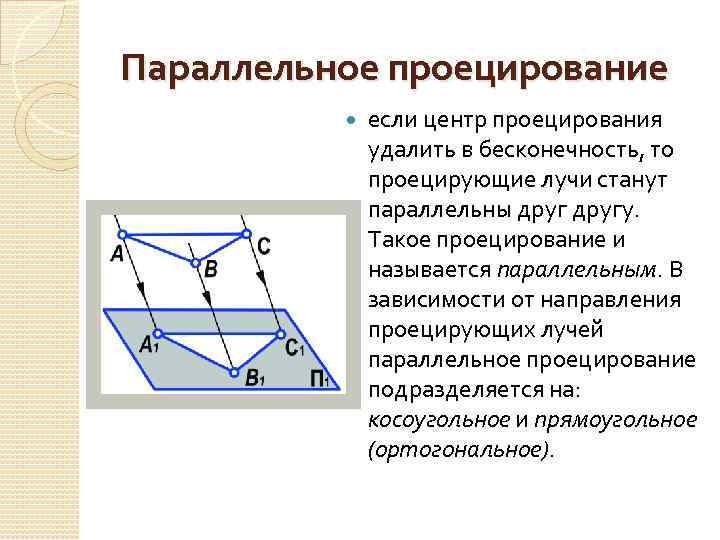 Параллельное проецирование если центр проецирования удалить в бесконечность, то проецирующие лучи станут параллельны другу. Такое проецирование и называется параллельным. В зависимости от направления проецирующих лучей параллельное проецирование подразделяется на: косоугольное и прямоугольное (ортогональное).
Параллельное проецирование если центр проецирования удалить в бесконечность, то проецирующие лучи станут параллельны другу. Такое проецирование и называется параллельным. В зависимости от направления проецирующих лучей параллельное проецирование подразделяется на: косоугольное и прямоугольное (ортогональное).
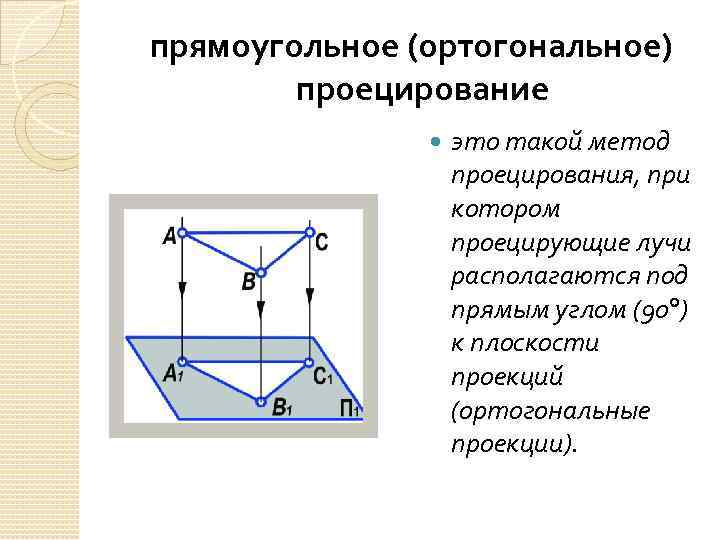 прямоугольное (ортогональное) проецирование это такой метод проецирования, при котором проецирующие лучи располагаются под прямым углом (90 ) к плоскости проекций (ортогональные проекции).
прямоугольное (ортогональное) проецирование это такой метод проецирования, при котором проецирующие лучи располагаются под прямым углом (90 ) к плоскости проекций (ортогональные проекции).
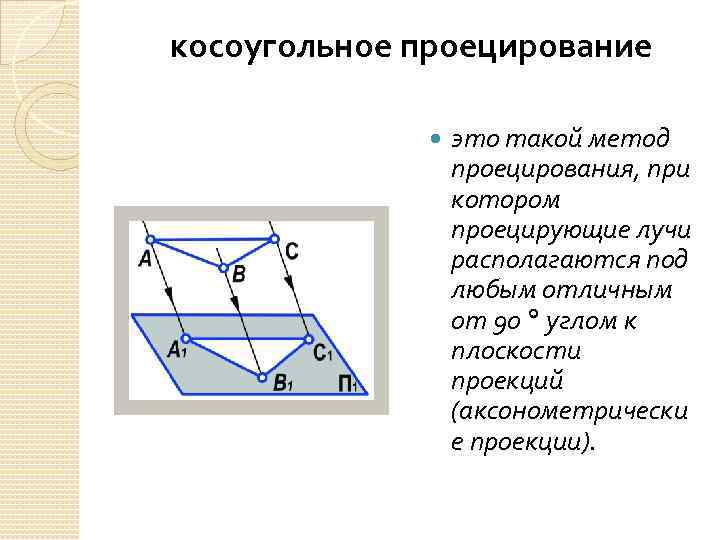 косоугольное проецирование это такой метод проецирования, при котором проецирующие лучи располагаются под любым отличным от 90 углом к плоскости проекций (аксонометрически е проекции).
косоугольное проецирование это такой метод проецирования, при котором проецирующие лучи располагаются под любым отличным от 90 углом к плоскости проекций (аксонометрически е проекции).
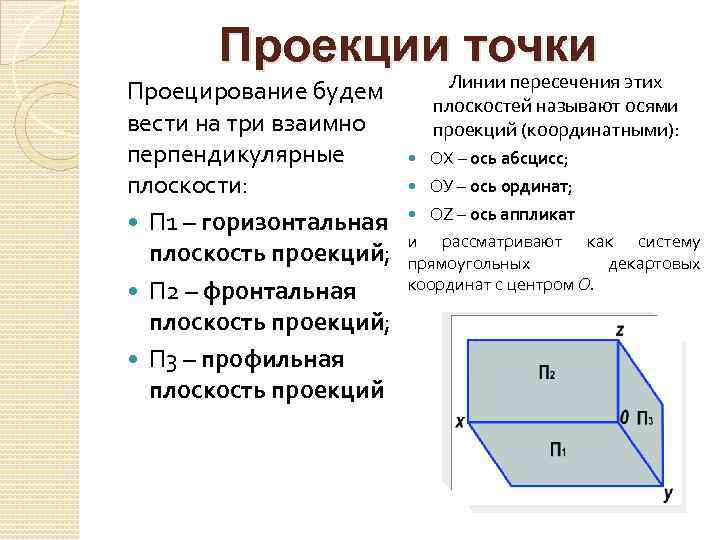 Проекции точки Проецирование будем вести на три взаимно перпендикулярные плоскости: П 1 – горизонтальная плоскость проекций; П 2 – фронтальная плоскость проекций; П 3 – профильная плоскость проекций Линии пересечения этих плоскостей называют осями проекций (координатными): ОХ – ось абсцисс; ОУ – ось ординат; ОZ – ось аппликат и рассматривают как систему прямоугольных декартовых координат с центром О.
Проекции точки Проецирование будем вести на три взаимно перпендикулярные плоскости: П 1 – горизонтальная плоскость проекций; П 2 – фронтальная плоскость проекций; П 3 – профильная плоскость проекций Линии пересечения этих плоскостей называют осями проекций (координатными): ОХ – ось абсцисс; ОУ – ось ординат; ОZ – ось аппликат и рассматривают как систему прямоугольных декартовых координат с центром О.
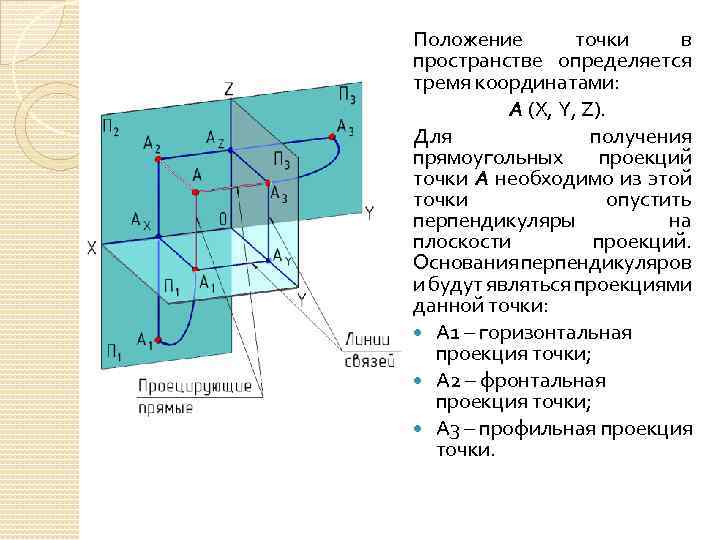 Положение точки в пространстве определяется тремя координатами: А (X, Y, Z). Для получения прямоугольных проекций точки А необходимо из этой точки опустить перпендикуляры на плоскости проекций. Основания перпендикуляров и будут являться проекциями данной точки: А 1 – горизонтальная проекция точки; А 2 – фронтальная проекция точки; А 3 – профильная проекция точки.
Положение точки в пространстве определяется тремя координатами: А (X, Y, Z). Для получения прямоугольных проекций точки А необходимо из этой точки опустить перпендикуляры на плоскости проекций. Основания перпендикуляров и будут являться проекциями данной точки: А 1 – горизонтальная проекция точки; А 2 – фронтальная проекция точки; А 3 – профильная проекция точки.
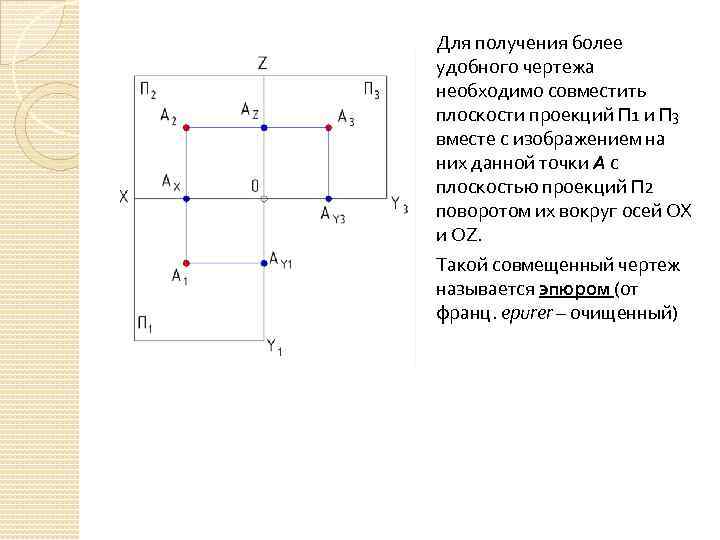 Для получения более удобного чертежа необходимо совместить плоскости проекций П 1 и П 3 вместе с изображением на них данной точки А с плоскостью проекций П 2 поворотом их вокруг осей ОХ и ОZ. Такой совмещенный чертеж называется эпюром (от франц. epurer – очищенный)
Для получения более удобного чертежа необходимо совместить плоскости проекций П 1 и П 3 вместе с изображением на них данной точки А с плоскостью проекций П 2 поворотом их вокруг осей ОХ и ОZ. Такой совмещенный чертеж называется эпюром (от франц. epurer – очищенный)
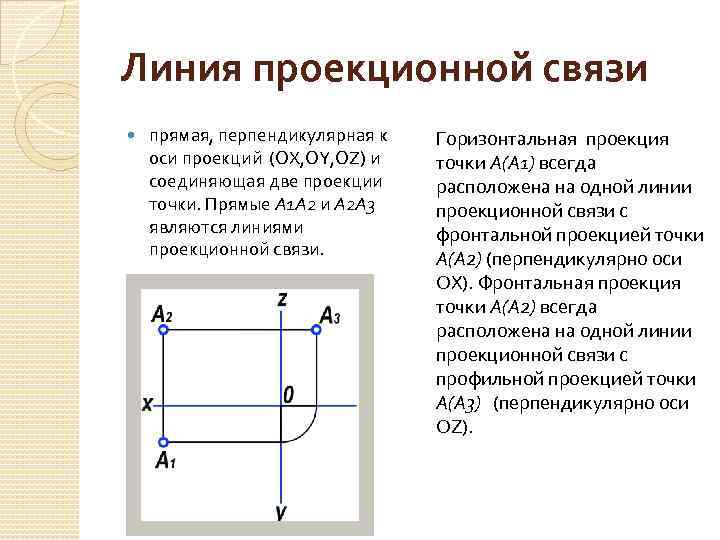 Линия проекционной связи прямая, перпендикулярная к оси проекций (OX, OY, OZ) и соединяющая две проекции точки. Прямые А 1 А 2 и А 2 А 3 являются линиями проекционной связи. Горизонтальная проекция точки А(А 1) всегда расположена на одной линии проекционной связи с фронтальной проекцией точки А(А 2) (перпендикулярно оси OX). Фронтальная проекция точки А(А 2) всегда расположена на одной линии проекционной связи с профильной проекцией точки А(А 3) (перпендикулярно оси OZ).
Линия проекционной связи прямая, перпендикулярная к оси проекций (OX, OY, OZ) и соединяющая две проекции точки. Прямые А 1 А 2 и А 2 А 3 являются линиями проекционной связи. Горизонтальная проекция точки А(А 1) всегда расположена на одной линии проекционной связи с фронтальной проекцией точки А(А 2) (перпендикулярно оси OX). Фронтальная проекция точки А(А 2) всегда расположена на одной линии проекционной связи с профильной проекцией точки А(А 3) (перпендикулярно оси OZ).