Раздел 1 Физические основы механики Курс лекций по

Раздел 1 Физические основы механики. Курс лекций по общей физики Доцент Петренко Л. Г. Кафедра общей и экспериментальной физики НТУ «ХПИ» Харьков - 2013 год

Раздел 1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ. Предмет механики. Кинематика и динамика. Классическая механика. Релятивистская механика. Квантовая механика. Механика – наука о механическом движении материальных тел и происходящих при этом взаимодействиях между ними. Классическая механика изучает движение макроскопических тел (их размеры и масса значительно больше, чем у атомов) со скоростями, много меньшими скорости света в вакууме (с=3. 108 м/с). Квантовая механика изучает движение микроскопических объектов (молекул, атомов, элементарных частиц). Релятивистская механика изучает макроскопических тел со скоростью света в вакууме. движение микро- и скоростями, сопоставимыми со

Основоположниками механики являются Галилео Галилей и Исаак Ньютон. Галилей открыл закон инерции, Ньютон сформулировал все сформулировал принцип относительности, обосновал модель Солнечной системы Коперника. основные законы механики – три закона динамики и закон всемирного тяготения.

1. 1. ЭЛЕМЕНТЫ КИНЕМАТИКИ 1. 1. 1. Механическое движение - простейшая форма движения материи. Физические модели: материальная точка (частица), система материальных точек, абсолютно твёрдое тело, сплошная среда. Понятия пространства и времени в классической механике. Пространственно-временные системы отсчёта. Кинематика и динамика. Механическое движение - простейшая форма движения материи. В философском смысле движение - это всякое изменение вообще. Движение - это способ существования материи. Материя и движение не существуют друг без друга. Кроме механической формы движения, существуют также физическое, химическое. биологическое и общественное движение. Движение тел происходит в пространстве и во времени. В классической механике пространство и время абсолютны. Пространство и время - формы существования материи.

В механике используются простые модели: - материальная точка (частица) - тело, имеющее массу, размерами которого в условиях рассматриваемой задачи можно пренебречь; - твёрдое тело - тело, размеры и форма которого не изменяется при движении; твёрдое тело можно представить как систему жёстко связанных материальных точек; - сплошная среда - непрерывно распределённая в пространстве среда, обладающая упругими свойствами. Для описания движения выбирается система отсчёта – совокупность системы координат и часов, связанных с телом, относительно которого рассматривается движение или равновесие других тел. В кинематике все системы отсчёта равноправны. Движение любого твёрдого тела можно представить как наложение поступательного и вращательного движения.

При поступательном движении любая прямая линия, жёстко связанная с телом, остаётся параллельной первоначальному положению. При вращательном движении твёрдого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Таким образом, сложное движение твёрдого тела можно разложить на две составляющие – поступательную и вращательную, и далее рассматривать движение только одной точки вдоль какой-либо линии (в частности, вдоль прямой или по окружности). Движение в механике можно описывать кинематически и динамически. Кинематика изучает движение тел без учёта причин, вызвавших это движение, т. е. в кинематике не учитывается взаимодействие тел. Основной задачей кинематики является установление способов задания движения тел и определение соответствующих кинематических характеристик – траектории, пути, перемещения, скорости, ускорения.

1. 1. 2. Кинематическое описание движения. Траектория, путь, перемещение. Скорость и ускорение в общем случае криволинейного движения. Траектория – это линия, которую описывает точка при своём движении. Уравнение траектории может быть представлено: - в аналитическом виде некоторой функцией: f(x, y, z) = 0; - в параметрическом виде: x = f 1(t), y = f 2(t), z = f 3(t); - в векторной форме. Расстояние между начальным (1) и конечным (2) положением точки, отсчитанное вдоль траектории, называется путём и обозначается S. Вектор, соединяющий начальное (1) и конечное (2) положение точки на траектории, называется вектором перемещения и обозначается.

Величина, характеризующая в каждый момент времени быстроту движения и направление перемещения, называется скоростью. В каждой точке вектор скорости направлен по касательной к траектории. Средняя скорость за промежуток времени (t, t+ t) равна: . Если промежуток времени t уменьшать, то в пределе получаем мгновенную скорость: Если ввести единичный вектор касательной , направленный в сторону перемещения точки, то вектор мгновенной скорости можно представить в виде: Модуль вектора мгновенной скорости равен: .

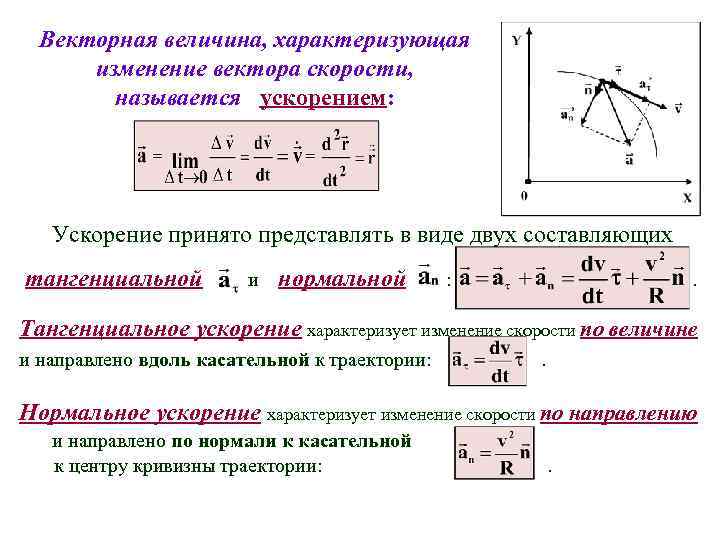Векторная величина, характеризующая изменение вектора скорости, называется ускорением: Ускорение принято представлять в виде двух составляющих тангенциальной и нормальной : . Тангенциальное ускорение характеризует изменение скорости по величине и направлено вдоль касательной к траектории: . Нормальное ускорение характеризует изменение скорости по направлению и направлено по нормали к касательной к центру кривизны траектории: .

Поступательное движение твёрдого тела можно свести к движению одной его точки (например, центра масс) вдоль произвольной траектории. Кинематический закон движения материальной точки вдоль произвольной траектории задаётся уравнением: . При равномерном движении (v=const) S является линейной функцией времени: . При равнопеременном движении (v=v 0+a t) S является квадратичной функцией времени: .

1. 1. 3. Угловая скорость и угловое ускорение точки, движущейся по окружности, и их связь с линейными скоростями и ускорениями. Основными кинематическими характеристиками вращательного движения являются угол поворота, угловое перемещение, угловая скорость и угловое ускорение. Угловое перемещение - это вектор, модуль которого равен углу поворота , а направление определяется правилом буравчика, т. е. вектор углового перемещения направлен вдоль оси вращения. Угловая скорость характеризует быстроту и направление вращения: Угловое ускорение характеризует быстроту изменения угловой скорости: Если угловая скорость возрастает, то вектор углового ускорения параллелен вектору угловой скорости. Если угловая скорость убывает, то вектор углового ускорения антипараллелен вектору угловой скорости.

Вращательное движение материальной точки задаётся уравнением: . При равномерном вращении ( =const) является линейной функцией времени: . При равнопеременном вращении ( = 0+ t) является квадратичной функцией времени: . Между кинематическими характеристиками поступательного и вращательного движения существует связь: где S - путь или длина дуги, по которой переместилась точка твёрдого тела при повороте его на угол , R - расстояние этой точки от центра вращения.

Кинематическое описание движения Соотношения между кинематическими характеристиками поступательного и вращательного движения S=R. , v=R. , a =. R, an= 2 R=v 2/R

1. 2. ДИНАМИКА ЧАСТИЦ 1. 2. 1. Понятие состояния в классической механике. Масса, сила, импульс и их единицы. Основная задача динамики. Динамика изучает движение тел под воздействием других тел. Для – это векторная величина, характеризующая взаимодействие тел, Силаописания действия тел друг на друга вводится понятие силы. в результате которого тела приобретают ускорения или деформируются. Сила определяется численным значением, направлением и точкой приложения. В природе существует четыре вида взаимодействий (4 вида сил): 1)гравитационное; 2)электромагнитное; 3)сильное ядерное; 4)слабое. В механике рассматриваются только - гравитационное и электромагнитное. На движение тела оказывает влияние его инертность. Свойство инертности проявляется в том, что различные тела при одинаковых воздействиях на них приобретают различные ускорения. Количественной мерой инертности тел является их инертная масса. Экспериментально доказана эквивалентность инертной и гравитационной масс.

Мерой механического движения является импульс (количество движения): В СИ единицей силы является 1 Н = 1 кг. м/с2 , единицей массы - 1 кг, единицей импульса - 1 кг. м/с = 1 Н. с. В классической механике состояние системы полностью определяется координатами и импульсами тел системы. Если известны начальное состояние системы и закон её движения (уравнение движения), то можно однозначно определить состояние системы в любой последующий момент времени. Существует два типа динамических задач: прямая (основная) задача - по действующим на тело силам определяют характер его движения; обратная задача - зная характер движение тела, определяют действующие на него силы. В основе классической механики лежат три закона Ньютона, полученные эмпирически (опытным путём).

1. 2. 2. Первый закон Ньютона (закон инерции). Понятие инерциальной системы отсчёта. 1 -ый закон Ньютона - закон инерции : материальная точка (или центр масс твёрдого тела) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит изменить это состояние. Системы отсчёта, в которых выполняется закон инерции, называются инерциальными системами, а в которых не выполняется - неинерциальными. Гелиоцентрическую систему отсчёта с большой точностью можно считать инерциальной. Геоцентрическая система строго не является инерциальной, поскольку все точки на поверхности Земли, кроме полюсов, движутся по окружностям, а значит, имеют центростремительное ускорение.

1. 2. 3. Второй закон Ньютона как уравнение движения. Импульс силы. Сила как производная импульса. Второй закон Ньютона - основной закон динамики : произведение массы материальной точки на её ускорение равно действующей на эту точку силе: Между понятиями сила и ускорение существует причинно-следственная связь – сила является причиной изменения состояния движения материальной точки, ускорение, приобретаемое точкой, является следствием действия на неё силы. В механике выполняется принцип независимости действия сил. Если на материальную точку действует несколько сил, то уравнение её движения имеет вид: Прямой или основной задачей динамики является нахождение ускорения по известным значениям действующих на материальную точку сил: Обратной задачей динамики является нахождение результирующей всех действующих на материальную точку сил по известному значению ускорения:

Поскольку ускорение определяет быстроту изменения скорости материальной точки и, если её масса не изменяется при движении, то второй закон Ньютона может быть сформулирован так – быстрота изменения импульса материальной точки определяется силой, действующей на неё: Формулировка второго закона Ньютона в таком виде является более точной, так как описывает движение не только материальных точек с постоянной массой, но и твёрдых тел, а также тел с переменной массой (реактивное движение). Именно в такой форме второй закон динамики был сформулирован И. Ньютоном в «Математических началах натурфилософии» в 1687 году. Если на материальную точку действует несколько сил, то быстрота изменения её импульса определяется результирующей всех действующих на неё сил: Если ввести величину, равную произведению силы на время её действия, называемую импульсом силы , то второй закон Ньютона может быть представлен в такой форме – изменение импульса материальной точки равно импульсу силы, действующей на неё: Действительно, при кратковременном действии даже очень больших сил на тела их состояние может практически и не измениться.

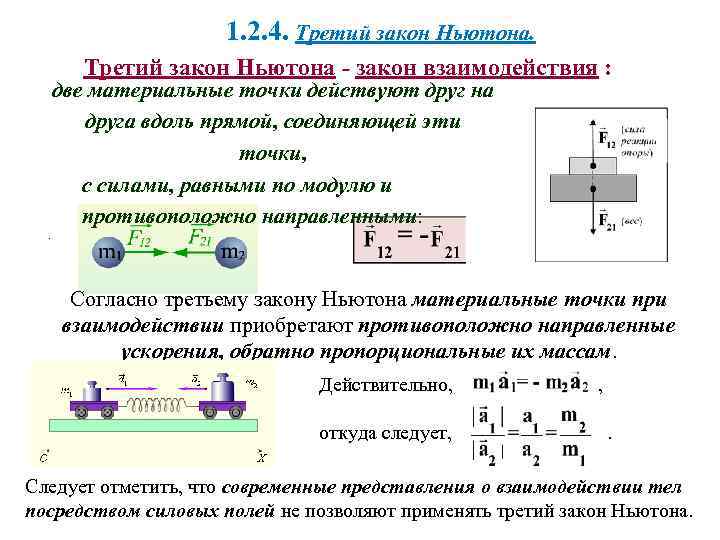1. 2. 4. Третий закон Ньютона - закон взаимодействия : две материальные точки действуют друг на друга вдоль прямой, соединяющей эти точки, с силами, равными по модулю и противоположно направленными: . . Согласно третьему закону Ньютона материальные точки при взаимодействии приобретают противоположно направленные ускорения, обратно пропорциональные их массам. Действительно, откуда следует, , . Следует отметить, что современные представления о взаимодействии тел посредством силовых полей не позволяют применять третий закон Ньютона.

1. 2. 5. Взаимосвязь и физическое содержание законов Ньютона. Механическая система. Внутренние и внешние силы. Современное толкование законов Ньютона. Границы применимости классического способа описания движения. Третий закон Ньютона в соединении с первым и вторым законами позволяет перейти от динамики отдельных материальных точек к динамике произвольной механической системы, а затем и твёрдого тела. В системе материальных точек (материальных тел) силы, действующие между точками (телами) этой системы, называются внутренними, а между точками (телами) системы и точками (телами), не входящими в систему, - внешними. Закон динамики для системы n материальных точек имеет вид: . Здесь - импульс механической системы n материальных точек; - главный вектор m внешних сил; векторная сумма внутренних сил, действующих между всеми n точками системы.

Согласно третьему закону Ньютона: Тогда . . Таким образом, уравнение, выражающее закон изменения импульса (второй закон Ньютона) для системы материальных точек, имеет вид: , где , Законы Ньютона выполняются только в классической механике, то есть в механике тел с массой, большей по сравнению с массой атомов (m>>mатом), движущихся со скоростями, малыми по сравнению со скоростью света (v<

1. 3. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА 1. 3. 1. Изолированная система как физическая модель. Закон сохранения импульса как фундаментальный закон природы и его связь с однородностью пространства. Механическая система, на которую не действуют внешние силы, называется изолированной или замкнутой системой. Импульс замкнутой системы материальных тел не изменяется с течением времени. В замкнутой системе : . В соответствии со 2 -ым законом Ньютона : А следовательно : . . В замкнутых инерциальных системах отсчёта не изменяются также и проекции импульса на оси декартовых координат: рх=const; py=const; pz=const.

Хотя закон сохранения импульса непосредственно следует из законов Ньютона, но он справедлив не только в рамках классической механики, но и в квантовой и в релятивистской механике. Импульсом могут обладать любые виды материи – не только частицы и тела, но и поля. Закон сохранения импульса является одним из фундаментальных законов природы и следует из важнейшего свойства симметрии пространства – его однородности. Понятие однородности пространства заключается в следующем – законы движения и физические свойства замкнутых систем не зависят от выбора начала координат инерциальной системы отсчёта, они не изменяются, если замкнутую систему переставить в пространстве как целое путём параллельного переноса.

1. 3. 2. Центр инерции (центр масс). Теорема о движении центра инерции. Система центра масс. Центром масс системы материальных точек называется точка, радиус-вектор которой равен: , где mi и - масса и радиус-вектор i-ой материальной точки; n - число материальных точек системы; - суммарная масса механической системы. Если масса системы непрерывно распределена по её объёму, то радиус-вектор центра элемента , где - радиус-вектор малого масс равен: системы, масса которого равна dm. Скорость центра масс равна: Отсюда следует, что импульс механической системы равен произведению массы этой системы на скорость её центра масс: .

Закон движения центра масс механической системы: Теорема о движения центра масс: центр масс механической системы движется как материальная точка, масса которой равна массе системы и на которую действует сила, равная главному вектору приложенных к системе внешних сил. Из теоремы о движении центра масс следует, что скорость центра масс замкнутой механической системы не изменяется с течением времени.

1. 4. ЗАКОНЫ ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА 1. 4. 1. Момент силы (вращательный момент). Момент импульса. Момент инерции материальной точки и твёрдого тела относительно оси. Уравнения динамики вращательного движения точки и твёрдого тела относительно оси. Уравнение моментов. Уравнения движения и равновесия твёрдого тела. При вращательном движении твёрдого тела все его точки движутся по окружностям, центры которых лежат на одной прямой линии, называемой осью вращения (ОО). Изменить состояние вращения тела может только тангенциальная к этим окружностям составляющая внешней силы , перпендикулярная радиусу-вектору, соединяющему центр вращения с точкой приложения силы. Таким образом, причиной изменения состояния вращательного движения является действие момента силы .

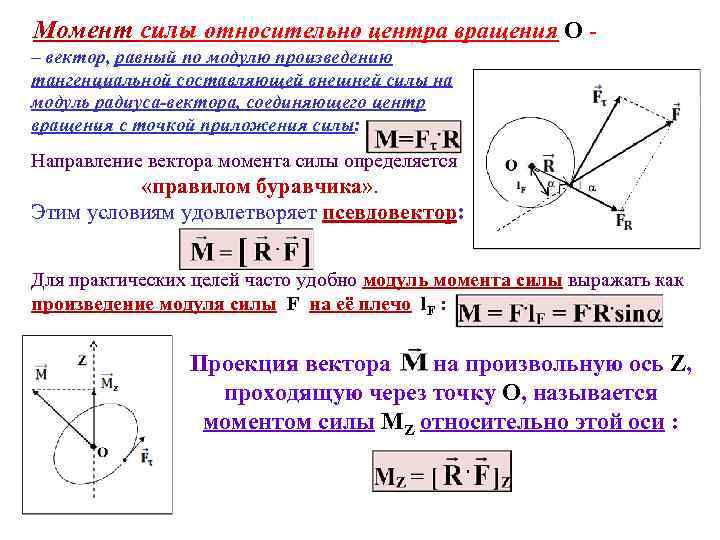Момент силы относительно центра вращения О – вектор, равный по модулю произведению тангенциальной составляющей внешней силы на модуль радиуса-вектора, соединяющего центр вращения с точкой приложения силы: . Направление вектора момента силы определяется «правилом буравчика» . Этим условиям удовлетворяет псевдовектор: Для практических целей часто удобно модуль момента силы выражать как произведение модуля силы F на её плечо l. F : . Проекция вектора на произвольную ось Z, проходящую через точку О, называется моментом силы МZ относительно этой оси :

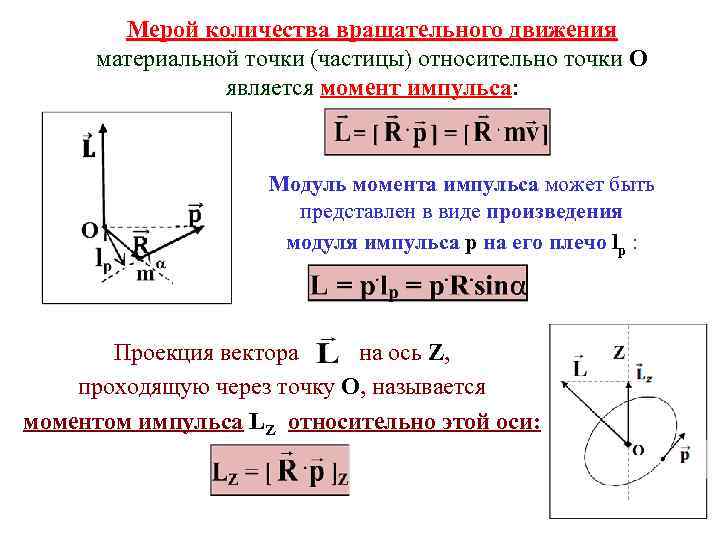Мерой количества вращательного движения материальной точки (частицы) относительно точки О является момент импульса: Модуль момента импульса может быть представлен в виде произведения модуля импульса p на его плечо lр : Проекция вектора на ось Z, проходящую через точку О, называется моментом импульса LZ относительно этой оси:

Изменение момента импульса частицы равно: Аналогичные уравнения могут быть записаны для системы материальных точек и для твёрдого тела. Закон изменения момента импульса является основным законом динамики вращательного движения материальной точки и твёрдого тела : Производная по времени от момента импульса частицы или твёрдого тела относительно оси равна моменту относительно той же оси сил, действующих на частицу или твёрдое тело:

Можно показать, что момент импульса LZ материальной точки или твёрдого тела относительно некоторой оси Z пропорционален угловой скорости Z их вращения относительно той же оси : LZ = I. Z. Коэффициент пропорциональности I называется моментом инерции. Момент инерции материальной точки массой m, находящейся на расстоянии r от оси вращения, равен: Момент инерции системы материальных точек: Момент инерции твёрдого тела относительно оси: где dm – элемент массы, находящийся на расстоянии r от оси вращения, - плотность вещества, V – объём тела.

Момент инерции твёрдого тела зависит от материала, его формы и размеров, а также от расположения его относительно оси вращения. Наиболее просто можно рассчитать моменты инерции тел правильной геометрической формы относительно оси вращения, совпадающей с их осью симметрии: однородного цилиндра (диска) с радиусом основания R – полого тонкого цилиндра (кольца) с радиусом основания R – однородного шара с радиусом R – , , . Момент инерции тонкого стержня длиною относительно оси, проходящей через центр масс и перпендикулярной стержню:

Расчёт моментов инерции твёрдых тел относительно оси Z, не проходящей через центр масс, осуществляется в соответствии с теоремой Штейнера: , где I 0 - момент инерции тела относительно оси, параллельной оси Z и проходящей через центр масс, d - расстояние между осями. Применяя теорему Штейнера, можно рассчитать момент инерции длинного стержня длиною относительно оси Z, перпендикулярной стержню и проходящей через один из его концов:

Поскольку LZ = I. Z , то скорость изменения момента импульса со временем равна : . закон динамики вращательного движения твёрдого тела относительно оси Z может быть представлен в виде: И таким образом, Если ось вращения твёрдого тела совпадает с главной осью инерции 1), то основной закон динамики вращательного движения имеет вид: где I – момент инерции тела относительно той же оси. 1) Главными осями инерции называются три взаимно перпендикулярные оси, проходящие через центр масс (центр инерции) тела.

При описании поступательного и вращательного движений твёрдых тел используются аналогичные характеристики: Импульс - мера количества поступательного движения (p=mv). Момент импульса -мера количества вращательного движения (L=I ). Масса - мера инертности движущихся твёрдых тел (m=F/a). Момент инерции – мера инертности вращающихся тел (I=M/ ). Отсюда следует и аналогия в записи основных уравнений поступательного и вращательного движения твёрдых тел:

Таким образом, движение твёрдого тела описывается двумя уравнениями: 1) - уравнение движения центра масс, - результирующая всех внешних сил; 2) - уравнение вращательного движения, - результирующий момент всех внешних сил. А условием равновесия твёрдого тела является выполнение одновременно двух равенств:

1. 4. 2. Закон сохранения момента импульса и его связь с изотропностью пространства. Момент импульса замкнутой системы относительно неподвижной точки не изменяется с течением времени: Момент импульса замкнутой системы относительно неподвижной оси не изменяется с течением времени: Закон сохранения момента импульса фундаментальный закон природы, являющийся следствием симметрии пространства – его изотропности – физические свойства и законы движения замкнутой системы не изменяются при повороте её в пространстве как целого на любой угол.

1. 5. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ 1. 5. 1. Энергия – универсальный способ описания движения и взаимодействия материальных объектов. Работа и её выражение через криволинейный интеграл. Мощность. Во многих физических процессах механическое движение переходит в другие формы движения материи, например, в тепловую, в химическую. В 1841 году Ю. Р. Майер впервые высказал идею о том, что все формы движения могут быть количественно определены одной и той же мерой - энергией. Энергия - это универсальная мера количества любых видов движения материи. В механике различают два вида энергии – кинетическую и потенциальную. Кинетическая энергия – это энергия механического движения системы. Потенциальная энергия – это энергия взаимодействия между телами. Мерой передачи механического движения от одного тела к другому при их взаимодействии или превращения механического движения в другие формы движения является физическая величина - работа.

Опытным путём установлено, что количество переданного материальной точке (отобранного у материальной точки) движения пропорционально произведению силы FS , действующей в направлении перемещения, на величину этого перемещения | |= S. Эта величина называется механической работой А. Измеряя работу А, можно определить изменение энергия W тела: А = W. Работа постоянной силы ( = const), составляющей угол с направлением вектора перемещения , равна: Частные случаи: 1) Fs 0 (0 ), А 0; в этом случае сила называется движущей; 2) Fs 0 ( ), А 0; в этом случае сила называется тормозящей; 3) Fs = 0 ( = ), А = 0; сила направлена перпендикулярно траектории – передачи движения нет.

Работа переменной силы F=f(s) на элементарном участке пути si = | | равна: . На всём пути от точки 1 до точки 2 работа равна: . Если s 0, то В математике такой интеграл называется криволинейным. На графике работа представляет собой площадь криволинейной трапеции, ограниченной осью абсцисс, кривой Fs(s) и вертикальными прямыми, проведенными через точки с координатами начального и конечного положения точки приложения силы. Способность механизмов совершать большую или меньшую работу за одно и то же время характеризует физическая величина – мощность. Единицей работы в СИ является 1 джоуль (1 Дж = 1 Н. м). Единицей мощности в СИ является 1 ватт (1 Вт = 1 Дж/с).

1. 5. 2. Кинетическая энергия механической системы и её связь с работой внешних и внутренних сил. Изменение кинетической энергии материальной точки происходит под действием силы и равно работе, совершаемой этой силой: Интегрирование этого уравнение при условии, что Wк= 0 для покоящейся точки (т. е. при v = 0 и p = 0), позволяет определить кинетическую энергию материальной точки: Кинетическая энергия системы материальных точек: Кинетическая энергия твёрдого тела массой m, движущегося со скоростью v: . Изменение кинетической энергии механической системы при малом её перемещении равно сумме работ, совершаемых при этом всеми внешними и внутренними силами: . Кинетическая энергия является функцией состояния движущейся механической системы и не зависит от её предыстории.

1. 5. 3. Работа, мощность и кинетическая энергия при вращательном движении тела. При вращательном движении твёрдого тела вокруг неподвижной оси вращательный момент создаёт только сила , касательная к траектории точки её приложения. Эта сила совершает работу: . . При повороте тела на угол = 2 - 1 совершается работа, равная: Кинетическая энергия малого элемента массой dm, отстоящего от оси вращения на расстоянии R, равна: . Кинетическая энергия твёрдого тела в целом равна: т. е. где . - момент инерции тела относительно оси вращения. Мощность при вращательном движении равна: .

1. 5. 4. Связь между кинетическими энергиями в различных системах отсчёта. Кинетическая энергия движения тела как целого. Значения скорости и кинетической энергии одной и той же материальной точки или механической системы различны в двух системах отсчёта, движущихся друг относительно друга. Теорема Кёнига – кинетическая энергия механической системы равна сумме кинетической энергии этой системы относительно системы её центра масс и кинетической энергии, которую имела бы она, двигаясь поступательно со скоростью её центра масс: При произвольном движении твёрдого тела его кинетическая энергия равна сумме кинетической энергии поступательного движения со скоростью его центра масс и кинетической энергии вращения тела вокруг мгновенной оси, проходящей через его центр масс (Ic – момент инерции тела относительно мгновенной оси):

1. 5. 5. Поле как форма материи, осуществляющая силовое взаимодействие между телами. Особая форма материи, связывающая частицы вещества в единую систему и передающая с конечной скоростью действие одних частиц на другие, называется физическим полем или прости полем. Механическое взаимодействие между телами происходит посредством связанных с ними гравитационного и электромагнитного полей. Не изменяющееся с течением времени поле называется стационарным. Поле называется однородным, если сила , действующая на частицу со стороны поля, одинакова во всех точках поля. Поле называется центральным, если направление силы , действующей со стороны поля на частицу в любой точке пространства, всегда проходит через одну точку, называемую центром поля (центром сил). При этом величина силы | | зависит только от расстояния частицы до центра поля. Такие силы называются центральными.

1. 5. 6. Консервативные и неконсервативные силы. Диссипация энергии. Силы, действующие в стационарном однородном поле, а также в центральном поле, являются консервативными, если их работа зависит только от начального и конечного положения частицы и не зависит от пути, по которому она двигалась. Работа консервативных сил на замкнутом пути равна нулю. Системы, в которых действуют консервативные силы, называются консервативными. Силы, работа которых зависит от формы пути, называются неконсервативными. Все силы, связанные с сопротивлением среды, являются неконсервативными. Работа неконсервативных сил на замкнутом пути не равна нулю. Системы, в которых действуют неконсервативные силы, При действииназываются неконсервативными. неконсервативных сил в замкнутой системе её механическая энергия постепенно уменьшается. Происходит диссипация энергии.

1. 5. 7. Потенциальная энергия частицы во внешнем силовом поле и её связь с действующей на частицу силой. Поле консервативных сил является частным случаем стационарного потенциального силового поля. Поле называется потенциальным, если его можно описать функцией П(х, y, z, t), называемой потенциальной, градиент которой определяет силу в каждой точке поля: . Если потенциальная функция не зависит от времени, то потенциальное поле является стационарным, а его силы – консервативными. В механике роль потенциальной функции играет потенциальная энергия Wп. Потенциальной энергией механической системы называется величина, равная работе, которую совершают все действующие на систему потенциальные силы при переводе системы из рассматриваемого состояния в исходное (нулевое, которое необходимо предварительно задать):

Работа консервативных сил при бесконечно малом изменении конфигурации системы равна убыли потенциальной энергии системы: d. A = - d. Wп. Измеряя работу потенциальных сил, можно определить изменение потенциальной энергии системы: В стационарных полях, зная потенциальную энергию Wп(x, y, z), можно определить силу, действующую на материальную точку со стороны поля:

1. 5. 8. Закон сохранения механической энергии и его связь с однородностью времени. Полная механическая энергия системы является суммой её кинетической и потенциальной энергии: W=Wк+Wп. Изменение полной механической энергии системы равно работе всех непотенциальных сил, действующих на систему при условии их стационарности: . Из закона изменения механической энергии следует закон сохранения механической энергии – полная механическая энергия системы тел, на которые действуют только консервативные силы, остаётся постоянной. Закон сохранения механической энергии связан с однородностью времени, то есть инвариантностью физических законов относительно выбора начала отсчёта времени.

1. 5. 9. Общефизический закон сохранения и превращения энергии как проявление несотворимости и неуничтожимости материи и её движения. Реальные механические системы неконсервативны, их механическая энергия не сохраняется. Опыт показывает, что в этом случае механическая энергия переходит в другие виды энергии, например, в тепловую или химическую. В 40 ых годах 19 века Ю. Майер, Дж. Джоуль и Г. Гельмгольц показали, что все процессы в природе подчиняются закону сохранения и превращения энергии.

Общефизический закон сохранения и превращения энергии: энергия системы может переходить из одной формы в другую и перераспределяться между частями системы, но изменение полной энергии в любом процессе всегда равно энергии, полученной системой извне в этом процессе. Этот закон является одним из важнейших законов природы и имеет глубокий философский смысл. Он является основой материалистического понимания явлений природы. Материя и её неотъемлемое свойство – движение несотворимы и неуничтожимы, а лишь преобразуются из одной формы в другую.

1. 6. ПРИНЦИПЫ ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ 1. 6. 1. Инерциальные системы отсчёта и механический принцип относительности Галилея. Преобразования Галилея. Инварианты преобразований Галилея. В 1632 году Галилео Галилей установил закон инерции, ввёл понятие инерциальных систем отсчёта и сформулировал механический принцип относительности, согласно которому все инерциальные системы отсчёта равноправны. Инерциальными называются системы отсчёта, в которых выполняются законы Ньютона. Механический принцип относительности Галилея законы механики не изменяются при переходе от одной инерциальной системы отсчёта к другой и формулируются одинаково во всех инерциальных системах отсчёта.

При переходе от одной инерциальной системы отсчёта к другой, движущейся относительно первой поступательно с постоянной скоростью, пользуются формулами преобразования координат и времени, называемыми преобразованиями Галилея. Инерциальная система отсчёта К* движется относительно инерциальной системы К со скоростью , направленной вдоль положительного направления оси Х. Если в начальный момент времени начала координат 0 и 0* обеих систем совпадали, то пространственные и временные координаты некоторой точки М в системах К и К* определяются уравнениями, называемыми преобразования Галилея в декартовых координатах: или в векторной форме: . х = х* + u t*; у = у*; z = z*; t = t*

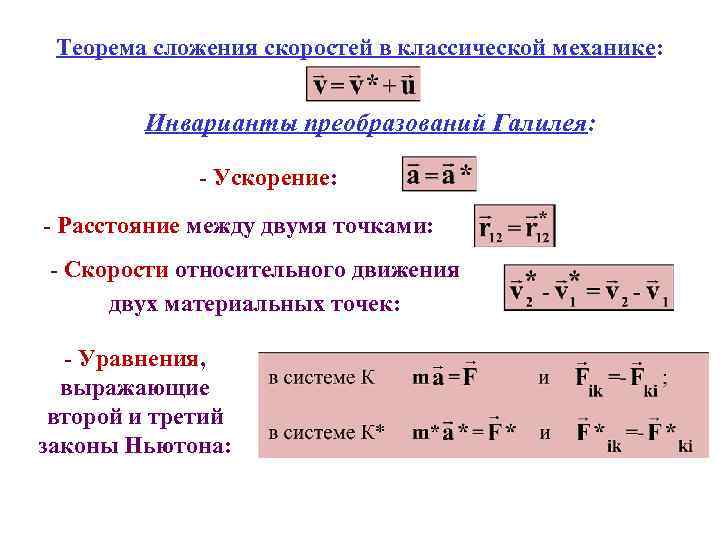Теорема сложения скоростей в классической механике: Инварианты преобразований Галилея: - Ускорение: - Расстояние между двумя точками: - Скорости относительного движения двух материальных точек: - Уравнения, выражающие второй и третий законы Ньютона:

1. 6. 2. Неинерциальные системы отсчёта. Силы инерции. Зависимость ускорения силы тяжести от географической широты. В неинерциальных системах отсчёта законы Ньютона не выполняются. Система отсчёта К*, движущаяся с ускорением , неинерциальна. Если формально ввести в этой системе силы инерции: то основной закон динамики материальной точки в неинерциальной системе отсчёта можно представить в виде: Вращающаяся система отсчёта имеет центростремительное ускорение: Сила инерции, действующая во вращающейся системе отсчёта, равна:

Эта сила называется центробежной силой инерции. Она всегда направлена по радиусу от центра вращения. Действием центробежной силой инерции обусловлена зависимость ускорения силы тяжести от географической широты . R Здесь m - масса тела; Мз - масса Земли; G - гравитационная постоянная; R - радиус Земли; r =Rcos - радиус окружности, по которой вращается тело, - географическая широта. Из уравнения динамики следует: Силы инерции реально действуют на материальную точку в неинерциальной системе отсчёта и могут быть в ней измерены. К силам инерции неприменим третий закон Ньютона. Неинерциальные системы отсчёта не могут быть замкнутыми. В неинерциальных системах отсчёта не выполняются законы сохранения импульса, момента импульса и энергии.

1. 6. 3. Релятивистская кинематика. Проблема пространства и времени. Постулаты специальной теории относительности. В 60 -е годы 19 века Дж. Максвелл завершил построение классической электродинамики и обосновал основные законы оптики. Один из важнейших выводов классической электродинамики заключается в утверждении, что скорость распространения электромагнитных взаимодействий не зависит от выбора инерциальной системы отсчёта и равна скорости распространения света. Этот факт противоречит классическому принципу относительности Галилея и классическому закону сложения скоростей. Опыты А. Майкельсона и Э. У. Морли в 1881 -1887 г. г. экспериментально доказали постоянство скорости света в вакууме. Противоречие между классической механикой и классической электродинамикой было устранено А. Эйнштейном в 1905 году в специальной теории относительности.

В основе теории Эйнштейна лежат два постулата: 1) релятивистский принцип относительности – в любых инерциальных системах отсчёта все физические явления при одних и тех же условиях протекают одинаково; то есть все инерциальные системы отсчёта равноправны; уравнения, выражающие все физические законы, имеют одинаковую форму во всех инерциальных системах отсчёта; 2) принцип инвариантности скорости света – скорость света в вакууме не зависит от движения источника света; то есть скорость света одинакова во всех инерциальных системах отсчёта и во всех направлениях. Опыты показывают, что скорость света в вакууме является предельной скоростью в природе и является одной из важнейших физических постоянных.

1. 6. 4. Преобразования Лоренца. Следствия из преобразований Лоренца: сокращение движущихся масштабов длин, замедление движущихся часов. Относительность одновременности. Из постулатов специальной теории относительности, а также однородности и изотропности пространства и однородности времени следует, что соотношения между координатами и временем одного и того же события в двух инерциальных системах отсчёта выражают преобразования Лоренца (а не Галилея, как в классической механике). Две инерциальные системы отсчёта К и К* имеют параллельные оси координат. Отсчёт времени начинается с момента, когда начала координат 0 и 0* совпадают. Система К* движется параллельно оси 0 Х с постоянной скоростью относительно системы К. . Преобразования Лоренца координат и времени при переходе из одной системы отсчёта в другую имеют вид:

Преобразования Лоренца приобретают симметричный вид, если вместо времени t ввести четвёртую координату ct (ct*) и обозначение : Для удобства математического описания теории относительности используют воображаемое четырёхмерное пространство – мир Минковского, координатами которого являются три пространственные координаты (х, у и z) и одна временная координата (ct). Событию в нём соответствует мировая точка, частице – мировая линия, параллельная оси времени ct. Из преобразований Лоренца следует понятие относительности одновременности – события, происходящие в один и тот же момент времени t в различных точках пространства неподвижной системы отсчёта К, в движущейся системе К* происходят в разные моменты времени t*.

Понятие относительности одновременности событий хорошо иллюстрирует следующий мысленный эксперимент. В движущейся параллельно оси 0 Х 1 системе К 1 источник излучает световой квант вдоль оси 0 Х 1 в обоих направлениях. Этот квант регистрируется одновременно двумя приёмниками, расположенными вдоль оси 0 Х 1 на равном расстоянии от источника. В неподвижной системе К квант света вначале зарегистрирует приёмник, находящийся ближе к началу координат, движущийся навстречу кванту, а затем второй приёмник, удаляющийся от кванта. Из преобразований Лоренца следует: 1) Лоренцевское сокращение длин - линейные размеры тела уменьшаются в направлении движения относительно инерциальной системы отсчёта: Здесь v – скорость тела в направлении движения; 0 = r 2* – r 1* - размер неподвижного тела; = r 2 – r 1 – размер движущегося тела; ri* и ri– координаты концов неподвижного и движущегося тел соответственно. Лоренцевское сокращение длин – кинематический релятивистский эффект, не связанный с действием каких-либо сжимающих сил.

Из преобразований Лоренца следует: 2) Относительность промежутка времени. Два события в системе К* происходят в моменты времени t 1* и t 2* в одной и той же точке пространства х1* = х2*. Промежуток времени между этими событиями в системе К* равен 0 = t 1* - t 2*. В системе К эти события произойдут в разных точках х1 и х2, причём х1 – х2 = v(t 1–t 2) = v , где = t 1 – t 2) - промежуток времени между этими событиями в системе К. . Тогда из преобразований Лоренца следует соотношение между промежутками времени между двумя событиями в системах отсчёта К и К*: Промежуток времени между двумя событиями минимален в той системе, в которой оба события совершаются в одной точке пространства. Это обуславливает релятивистский эффект замедления времени – часы, движущиеся со скоростью v относительно данной инерциальной системы отсчёта, идут медленнее, чем неподвижные.

1. 6. 5. Закон сложения скоростей в релятивистской кинематике может быть получен из преобразований Лоренца: При u << c этот закон совпадает с законом сложения скоростей в классической механике: Если скорость какой-либо точки М в одной из инерциальных систем отсчёта, например, в системе К* равна с, то и в любой другой системе, например, в системе К, она будет равна с.

1. 6. 6. Инварианты преобразований Лоренца как проявление взаимосвязи пространства и времени. В релятивистской механике при переходе от одной инерциальной системы отсчёта к другой промежутки времени и отрезки длины изменяются. В отличие от классической механики, они не являются инвариантами относительно преобразований координат и времени Лоренца. Инвариантом преобразований Лоренца является пространственно-временной интервал: Используя преобразования Лоренца, можно показать, что в системах отсчёта К и К* выполняется равенство интервалов: Инвариантность пространственно-временного интервала является отражением неразрывной связи пространства и времени.

1. 7. ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ ДИНАМИКИ 1. 7. 1. Релятивистский импульс. Уравнение движения релятивистской частицы. Инвариантность уравнения движения относительно преобразований Лоренца. Принцип относительности Эйнштейна утверждает, что все уравнения, описывающие законы природы, должны быть инвариантными относительно преобразований Лоренца. Однако уравнения классической механики Ньютона оказались неинвариантными, и поэтому СТО потребовала пересмотра и уточнения законов механики. В основу такого пересмотра Эйнштейн положил требования выполнимости законов сохранения импульса и энергии в замкнутых системах. Для того, чтобы закон сохранения импульса выполнялся во всех инерциальных системах отсчета, необходимо было изменить определение импульса тела. Вместо классического импульса в СТО релятивистский импульс тела с массой m, движущегося со скоростью , записывается в виде:

Основное уравнение релятивистской динамики: или . Это уравнение инвариантно относительно преобразований Лоренца. При малых скоростях частицы v << c оно переходит в классическое уравнение, выражающее второй закон Ньютона. При увеличении скорости материальной частицы и приближении её значения к скорости света в вакууме (v → c) импульс этой частицы неограниченно возрастает (рр→∞). Поскольку в природе нет реальных сил, которые могли бы сообщить частице бесконечно большой импульс, то и скорость материальной частицы относительно любой инерциальной системы отсчёта не может достичь скорости света в вакууме. Другими словами, скорость материальных частиц всегда меньше скорости света в вакууме.

1. 7. 2. Работа и энергия. Преобразования импульса и энергии. Законы сохранения энергии и импульса в релятивистской механике. Если на релятивистскую частицу действует сила и при перемещении её на совершается работа d. A , то изменяется, соответственно, и кинетическая энергия этой частицы: Применение основного закона релятивистской динамики и интегрирование этого уравнение при условии, что Wк = 0 при v = 0, позволяет получить уравнение, выражающее кинетическую энергию релятивистской частицы: . При v << c уравнение, выражающее релятивистскую кинетическую энергию, преобразуется в классическую формулу : . Если не учитывать потенциальную энергию частицы во внешнем силовом поле, то её полная энергия определяется суммой кинетической энергии Wк и энергии покоя : .

Если не учитывать потенциальную энергию частицы во внешнем силовом поле, то согласно теории А. Эйнштейна полная энергия частицы определяется суммой кинетической энергии Wк и энергии покоя , пропорциональной массе неподвижной в данной системе отсчёта частицы: Если ввести понятие релятивистской массы: , то полная энергия движущегося объекта окажется пропорциональной релятивистской массе: . Таким образом был установлен фундаментальный закон природы – закон взаимосвязи (пропорциональности) массы и энергии: полная энергия механической системы равна произведению её релятивистской массы на квадрат скорости света в вакууме.

Закон взаимосвязи массы и энергии подтверждён многочисленными экспериментами в ядерной физике (при осуществлении ядерных реакций и превращении элементарных частиц). Между полной энергией и импульсом частицы существует релятивистское соотношение : В релятивистской механике, как и в классической, выполняются фундаментальные законы природы – законы сохранения энергии и импульса: - в силу однородности времени полная энергия замкнутой системы тел сохраняется, то есть не изменяется с течением времени; - в силу однородности пространства релятивистский импульс замкнутой системы тел сохраняется, то есть не изменяется с течением времени. .

В специальной теории относительности рассматриваются инерциальные системы отсчёта. Распространение идей специальной теории относительности на неинерциальные системы отсчёта позволило А. Эйнштейну создать общую теорию относительности. В основе общей теории относительности лежит принцип эквивалентности тождественности инертных масс всех тел их гравитационным массам. А. Эйнштейн предложил для неинерциальных систем отсчёта ввести эквивалентное поле сил тяготения. Релятивистская механика в предельном случае малых скоростей (v<

Благодарю за внимание