Ray Space Factorization for From-Region Visibility Tommer Leyvand

Ray Space Factorization for From-Region Visibility Tommer Leyvand Olga Sorkine Daniel Cohen-Or Tel-Aviv University, Israel

From-Region Visibility Problem of identifying which parts are visible from a region (viewcell) Entire Model Visibility Set Valid from within the viewcell

Abstract • Conservative occlusion culling method – Factorizing 4 D visibility problem in to horizontal and vertical components • Two components is solved asymmetrically • Horizontal component – Parameterization of the ray space • Vertical component – Incrementally merging umbrae

Abstract • Efficiently realized together by modern graphics hardware • Occlusion map to encode visibility • Culling time and size of the computed PVS → depend on the size of the viewcell • For moderate viewcells – Occlusion culling of large urban scenes: < 1 sec – Size of the PVS = 2 * size of the exact VS

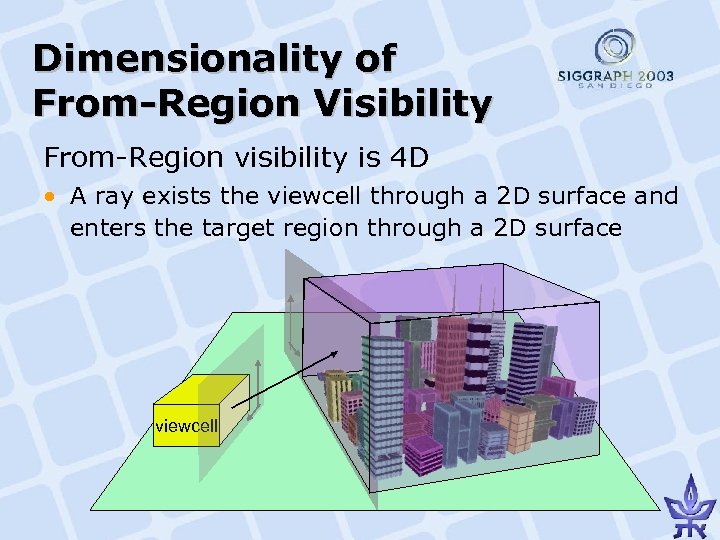
Dimensionality of From-Region Visibility From-Region visibility is 4 D • A ray exists the viewcell through a 2 D surface and enters the target region through a 2 D surface viewcell

Our Factorization Factor the 4 D visibility problem into horizontal and vertical components Ray Space Approach Horizontal direction Umbra Merging Approach Vertical direction

Form-Pint vs. From-Region • Complexity of models keeps growing • Occlusion culling can effectively reduce the rendering depth complexity • Visibility from-point: compute each frame • Visibility from-region: valid for a region rather than a single point – Advantage of time and spatial coherence – Computational cost is amortized over consecutive frames • Compute from-region visibility on-the-fly, not having to resort to off-line methods

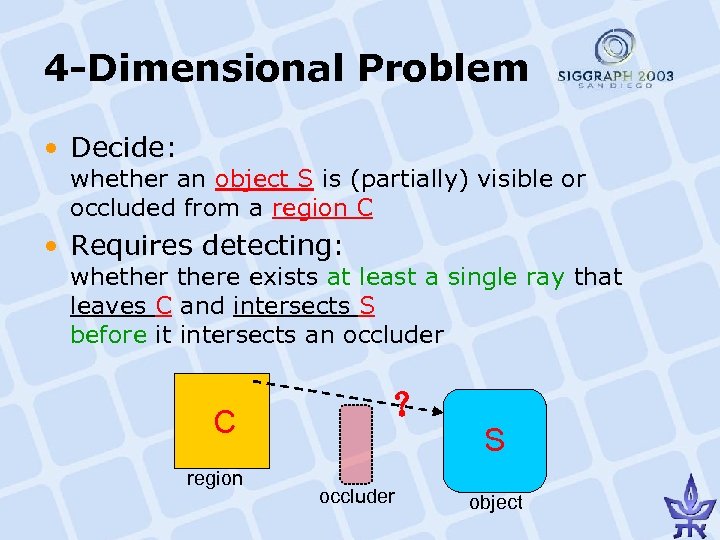
4 -Dimensional Problem • Decide: whether an object S is (partially) visible or occluded from a region C • Requires detecting: whethere exists at least a single ray that leaves C and intersects S before it intersects an occluder C region ？ occluder S object

Solutions • Exact solutions are possible: ！overly expensive！ [Nirenstein et al. 2002…] • Conservative solutions: [Durand et al. 2000…] gain speed-up by overestimating the exact VS • Dealing with 2. 5 D scenes: [Koltun et al. 2001…] 2. 5 D occluders is quite reasonable in practice (especially in walkthrough applications) • For more general scenes – Necessary to have a culling method that can deal with the occlusion of a larger domain of shapes

Graphics Hardware • Advanced graphics cards: visibility feature indicates whether a just drawn polygon is visible or hidden by polygons already drawn • The technique this paper present here: utilizes capabilities of the latest graphics hardware to accelerate the performance for fromregion visibility

Occlusion Culling Method • Occlusion cast: arbitrary 3 D models • Idea: 4 D visibility problem → two 2 D components – Horizontal: parameterization of the ray space – Vertical: maintained by pairs of occluding angles • Key point: – Horizontal components → polygonal shapes – Each point in polygonal footprints → vertical slice – Modern graphics hardware → polygonal footprints can be drawn – Applying per-pixel visibility calculations → significant speed-up

From-region Method • Early generic from-region methods: occlusion of a single occluder or approximated • Better capture the occlusion and reduce the VS: detect objects – hidden by a group of occluders • Advanced from-region methods: aggregating individual umbrae into a large umbra capable of occluding larger parts of the scene

Aggregating Umbrae • Ray-parameterization: – capture the visibility of an object into some geometric region (a polygonal footprint) – Apply Boolean operations (visibility) • Fuses individual intersecting umbrae into large umbrae • Combines these two approaches！

Occlusion Problem • Visibility problems: (in particular occlusion problem) → problems in line spaces • Example: basic occlusion problem Given a segment C, an object A is occluded from any point on C by a set of objects Bi →if all the lines intersecting C and A 　also intersect the union of Bi A C

Occlusion Problem – Solution • Using the line space, lines in the primal space mapped to points • Mapping: 2 D line vs. point Define: By coefficients of the lines (primal space) line y = ax + b is mapped to point (a, -b) (in the line parameter space) footprint A C

Occlusion Problem – Analysis • Not optimal: vertical lines are mapped to infinity • Problem: all lines with large coefficients • Practical reason: dual space must be bounded • Solution: moving to higher dimensions – Loses the simplicity and efficiency of operating in image space

Occlusion Problem – Analysis • Ideas to 3 D case: not as easy as in 2 D the parameter space of 3 D lines has high D • In general, 3 D lines have four DOF • Rays: origin of the lines • Visibility in 2 D flatland: limited interest • Note: most of objects are detected as occluded in flatland, while actually being visible in 2. 5 D due to their various heights

Occluder Fusion • Different approach for occluder fusion: incrementally construct an aggregate umbra in primal space • Occluder fusion occurs whenever: individual umbrae intersect • Note: umbra intersection is a sufficient condition but not necessary one

Overview • Bounded nonsingular parameterization: 2 D component by a vertical projection of the objects onto the ground (z=0) • Footprint: composed of a polygons (parameter space) • Rays in 3 D primal space = (s, t) direction define a vertical slice (directional plane)

Overview 　 Line segment: casts a directional umbra → each directional plane: aggregated umbra (occluder) → aggregated umbra (all): maintained in occlusion map

Overview • Hierarchical front to back traversal of objects – Perform visibility queries – Update the occlusion map • Footprint of objects – Conservatively discretized – Drawn by the graphics hardware • Occlusion map – Represented by a discrete ray space

Ray Parameterization • Duality of R 2 is a correspondence between – 2 D lines y=ax+b in the primal space – Points (a, -b) in the dual space • Different parameterization of 2 D lines – Only the oriented lines (rays) (emerge from a given 2 D square viewcell) – Not have singularity – Parameter space is bounded – Rays (leave the viewcell) intersect a triangle • Form a footprint in the parameter space – Can be represented by a few polygons

Primal Space t=0 1/4 s=0 3/4 1/4 1/2 Primal Space • s, t: associated with the inner, outer squares • r(sr, tr) : ray r intersects with inner and outer squares

Footprint of a 2 D Triangle • Footprint: a geometric primitive as the set of all points in the parameter space that refer to rays that intersect the primitive t=0 1/4 s=0 t 1/2 1/4 tq 1(1) tq 1(1/4) q 1 tq 1(3/4) tq 1(1/2) 3/4 1/2 3/4 A q 2 tq 1(1/2) tq 1(1/4) 1/4 1/2 Primal Space -- For a fixed value of s: { (s, t) : t 0 1/4 1/2 3/4 Ray Parameter Space [tq 1(s), tq 2(s)] } 1 s

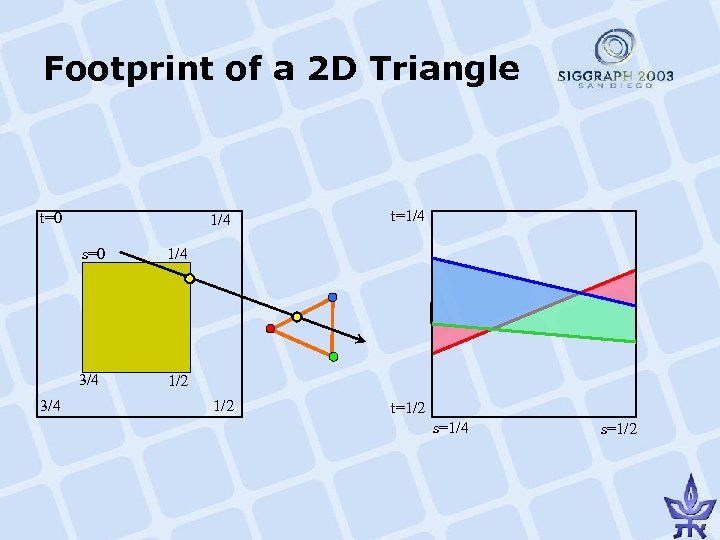
Footprint of a 2 D Triangle 1/4 t=0 s=0 3/4 1/2 t=1/2 1/4 3/4 t=1/4 1/2 s=1/4 s=1/2

Visibility within a Vertical Plane • Traverse the cells of a kd-tree in a front-to -back order interleave occlusion tests against the occlusion map and umbra merging to maintain it • How to perform visibility queries? • How to perform occluder fusion?

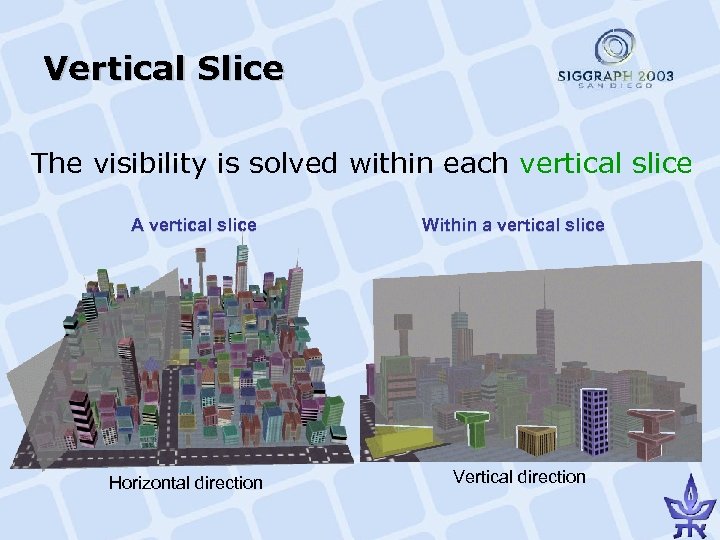
Vertical Slice The visibility is solved within each vertical slice A vertical slice Horizontal direction Within a vertical slice Vertical direction

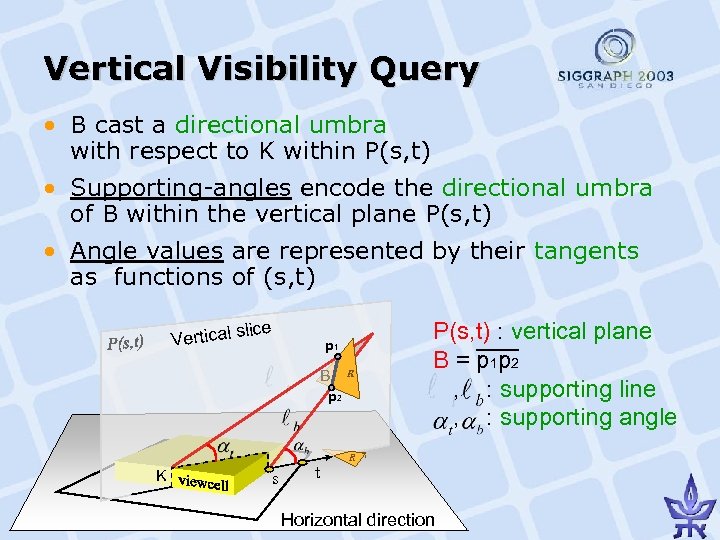
Vertical Visibility Query • B cast a directional umbra with respect to K within P(s, t) • Supporting-angles encode the directional umbra of B within the vertical plane P(s, t) • Angle values are represented by their tangents as functions of (s, t) ice sl Vertical p 1 B R p 2 K s t P(s, t) : vertical plane B = p 1 p 2 , : supporting line , : supporting angle R ‘ Horizontal direction

Vertical Visibility Query • Q: line segment within P(s, t) that’s behind B (according to the front-to-back order with respect to the viewcell) • Determining whether Q is occluded by B →Testing whether the umbra of B contains Q • Front-to-back order guarantees – tested segment is always behind the occluders →supporting lines are sufficient for the visibility test Directional accumulated umbra Q is occluded: Both of their endpoints are within the accumulated umbra i. e. Within a slice: Test occlusion by comparing supporting angles

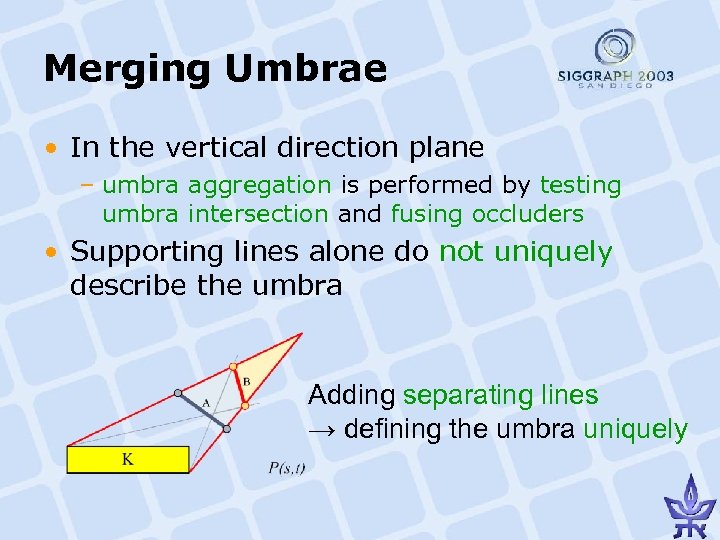
Merging Umbrae • In the vertical direction plane – umbra aggregation is performed by testing umbra intersection and fusing occluders • Supporting lines alone do not uniquely describe the umbra Adding separating lines → defining the umbra uniquely

Merging Umbrae (1) Umbra of one segment is contained in the area between the supporting lines of the other segment “throw out” the contained segment and keep just the other one

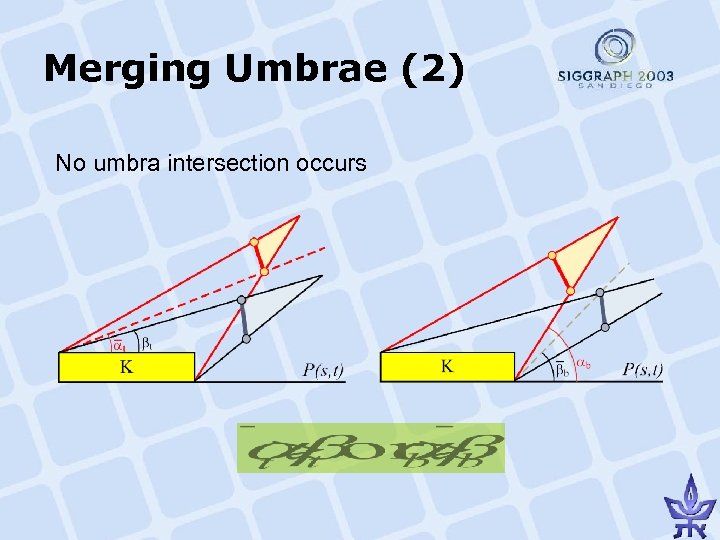
Merging Umbrae (2) No umbra intersection occurs

Merging Umbrae (3) If (1)(2) tests fail as well → umbra intersection Replace the two segments by a new “virtual” occluder segment Insert into the occlusion map the following angles:

Occluder Fusion • Note: – Fused umbra is valid only for testing occlusion of ocludees placed behind all the occluders that created the umbra – Merging umbra is order-independent • an approximate ordering of the occluders is more efficient – Typically man-made scenes have a strong vertical coherence and after some umbra-merging steps, the umbra grows to capture most of the occlusion

Putting It All Together • Combine: horizontal footprint, vertical visibility – Exploiting－all the directional (vertical) computations can be performed in parallel • Footprints are conservatively discretized before rendering – adding four values {v 0, v 1, v 2, v 3} to each pixels – represent the four supporting and separating angles

Umbra Encoding • For each vi: – footprint F(R’) is augmented into a 3 D (s, t, v) parameter space, yielding four 3 D footprints – these footprints are surface ection ertical dir V v t (s, t) Horizontal direction Parameter Space s

Hierarchical Visibility Culling • Original objects of the scene are inserted into a kd-tree • During the algorithm, kd-tree has two functions – traverse the scene in a front-to-back order – allows culling of large portions of model

Kd-tree traverse • Kd-tree is traverse top-down – large cells can be detected as hidden and culled with all their sub-tree – if a leaf node is still visible • the visibility of each bounding box associated with it is tested – if a bounding box is visible • the triangles bounded in it are defined as potentially visible

Occlusion • In scenes with significant occlusion – objects close to the viewcell rapidly fill the occlusion map – most of the back larger kd-cells are detected as hidden • From-region front-to-back order of the kdcells is a strict order rather than approximate – guaranteed by using large kd-cells whose splitting planes never intersect any viewcells

Merging Umbra • Merging umbra is applied while traversing the kd-tree front-to-back – a leaf node is detected as visible • the polygons in that leaf are considered as occluders and their footprint are inserted into the occlusion map (possibly merging with the existing umbrae created so far) • Merging umbrae simplifies the occlusion map and increases the occlusion – optionally, before updating the occlusion map, the visibility of individual polygons in the PV leaf can be tested to tighten the PVS

Algorithm PVS← Calculate. Visibility(kd-tree. root) Calculate. Visibility(curr_kd_cell) if Test. Visibility(curr_kd_cell) //current kd-cell is visible if cur_kd_cell. Is. Leaf() PVS←PVS curr_kd_cell. get. Triangles() Augment. Occlusion. Map(curr_kd_cell. get. Rriangles()) else foreach kd_child curr_kd_cell. children in f 2 b order Calculate. Visibility(kd_child) end foreach endif else return //current kd-cell occluded->terminate end

2. 5 D Occluders • 2. 5 D occluders: “half-umbra” – only top supporting angle is stored – bottom supporting angle is always zero – encode using the z-coordinate of the 2 D footprint • Testing visibility of an occludee – testing the visibility of its footprint (disabling zbuffer) • Umbra fusion by – enabling z-buffer updates – drawing the occluder footprint

3 D Occluders • Use a series of top and bottom supporting and separating angles • Occlusion map stores only a single directional umbra per direction (hardware limitation) • Testing visibility of an occludee – testing whether the top or bottom supporting footprints are visible • Umbra fusion by – testing whether the new umbra intersects the current umbra in the occlusion map

Implementation • Cg implementation: – 32 bit floating-point PBuffer • store the global occlusion map – Fragment shader functionality • calculation of the directional umbra within each slice • testing occlusion • merging umbra

Urban Model • 2 GHz P 4 machine with Nvidia Ge. Force 4 Ti graphics card • A randomly generated urban model: – Large set of parameters – Increasing vertical complexity – Not axis-aligned

Non-realistic Model • Box-field: consists of randomly generated boxes – Not too dense → geometry deep inside the box-field is visible – Reducing the effectiveness of the use of a hierarchy

Result-Urban Scene Off-junction viewcells In-junction viewcells Viewcell size Time PVS / VS 3 0. 31 2412 / 1760 0. 40 8832 / 6824 9 0. 41 2840 / 2632 0. 51 12184 / 9072 14 0. 58 3592 / 2894 0. 96 13576 / 9184 20 0. 71 4568 / 2928 1. 56 18340 / 9888 25 0. 78 5224 / 2960 2. 01 21608 / 10072 • • • 26. 8 M triangles Height of viewcells: 2. 5 units PVS and VS size is given in triangles Time: refers to culling-time (seconds) Off-junction viewcells: within some city block In-junction viewcells: on the junction of two long avenues

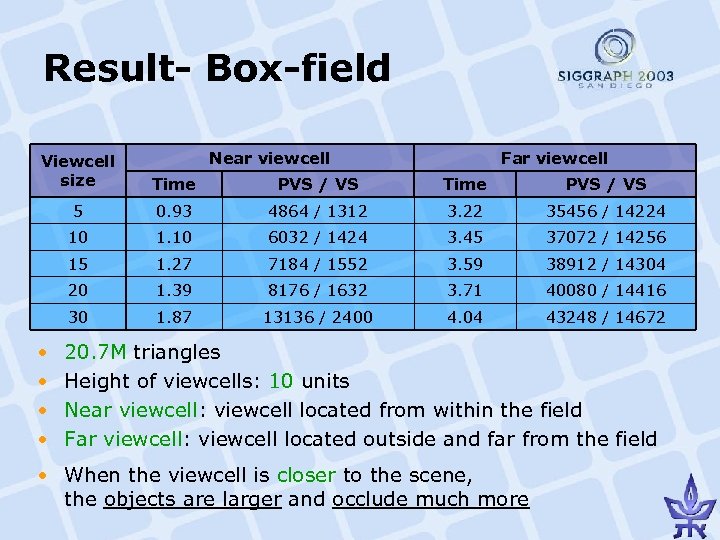
Result- Box-field Near viewcell Far viewcell Viewcell size Time PVS / VS 5 0. 93 4864 / 1312 3. 22 35456 / 14224 10 1. 10 6032 / 1424 3. 45 37072 / 14256 15 1. 27 7184 / 1552 3. 59 38912 / 14304 20 1. 39 8176 / 1632 3. 71 40080 / 14416 30 1. 87 13136 / 2400 4. 04 43248 / 14672 • • 20. 7 M triangles Height of viewcells: 10 units Near viewcell: viewcell located from within the field Far viewcell: viewcell located outside and far from the field • When the viewcell is closer to the scene, the objects are larger and occlude much more

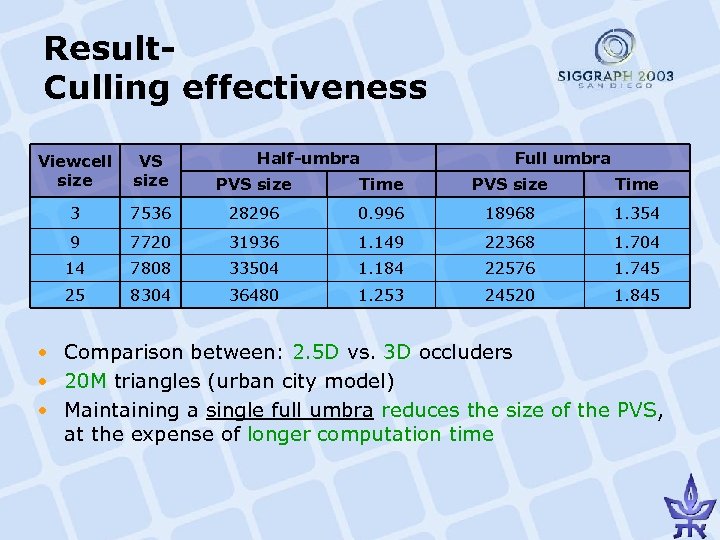
Result. Culling effectiveness Half-umbra Full umbra Viewcell size VS size PVS size Time 3 7536 28296 0. 996 18968 1. 354 9 7720 31936 1. 149 22368 1. 704 14 7808 33504 1. 184 22576 1. 745 25 8304 36480 1. 253 24520 1. 845 • Comparison between: 2. 5 D vs. 3 D occluders • 20 M triangles (urban city model) • Maintaining a single full umbra reduces the size of the PVS, at the expense of longer computation time

Result • Culling time is directly dependent on two interdependent factors – number of visibility queries – number of visible triangles (occluders) • The technique can deal with a huge model – due to the hierarchy – but only as long as the size of the VS is small • only a small number of triangles is visible • implies that only a small number of kd-cells in the hierarchy is tested

Result • PVS: quite conservative – Absolute size of the PVS is relatively small (less than 0. 1% of the full model) • Effectiveness – Not measured for a single view – Over time, for a large number of frames – 30 FPS->at least hundreds of frames are generated within one viewcell – actual cost of generating the PVS can be amortized over time

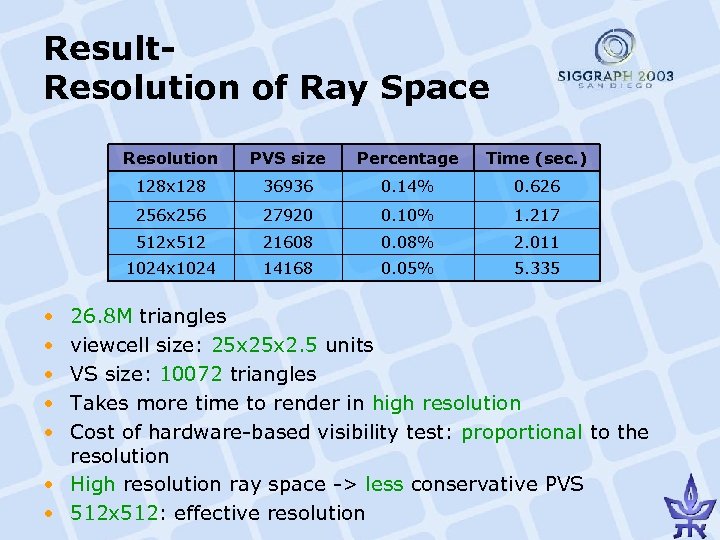
Result. Resolution of Ray Space Resolution Percentage Time (sec. ) 128 x 128 36936 0. 14% 0. 626 256 x 256 27920 0. 10% 1. 217 512 x 512 21608 0. 08% 2. 011 1024 x 1024 • • • PVS size 14168 0. 05% 5. 335 26. 8 M triangles viewcell size: 25 x 2. 5 units VS size: 10072 triangles Takes more time to render in high resolution Cost of hardware-based visibility test: proportional to the resolution • High resolution ray space -> less conservative PVS • 512 x 512: effective resolution

Result. Culling effectiveness Small viewcells Large viewcells Size PVS/VS Size Time PVS/VS 3 0. 18 946 / 424 50 0. 36 3396 / 502 14 0. 19 1216 / 514 100 0. 45 4424 / 744 25 • • • Time 0. 22 1546 / 592 150 0. 58 5720 / 930 Vienna 200 model: 3 x 3 km of the city Height of buildings: 2. 2 -50. 8 m (18. 6 m on average) Size: viewcell in meters (height of viewcells is 2 m) For smaller viewcells: PVS is tight (2 -2. 6) For large viewcells: PVS/ VS ratio grows to about 6 -7

The End Before After

Procedural City XML configured city generation engine • Simple building blocks – 3 D boxes and pyramids – Rotation and scaling operators – Texture groups – Instantiation parameters within user defined random limits • Exports city to VRML 2. 0