Равносильные и неравносильные преобразования при решении уравнений
Равносильность и логическое следование Два уравнения называются равносильными, если корни одного из них являются корнями другого и наоборот. l Если оба уравнения не имеют корней, то они тоже считаются равносильными. l Если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называют следствием первого. l
Найти ошибку в решении уравнения Ответ: -1; 2.
Найти ошибку в решении системы уравнений Разделим первое уравнение системы на второе: Ответ: (6; 4/5)
Найти ошибку в решении уравнения Ответ: ; -
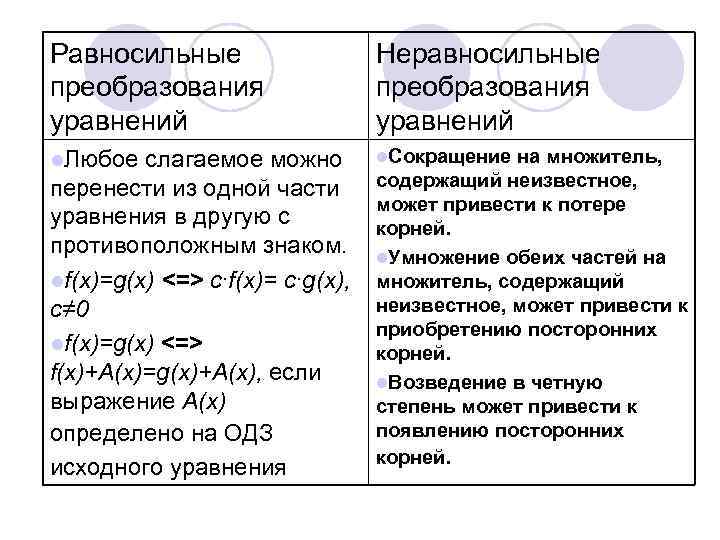
Равносильные преобразования уравнений Неравносильные преобразования уравнений l. Любое l. Сокращение слагаемое можно перенести из одной части уравнения в другую с противоположным знаком. lf(x)=g(x) <=> с∙f(x)= с∙g(x), с≠ 0 lf(x)=g(x) <=> f(x)+А(х)=g(x)+А(х), если выражение А(х) определено на ОДЗ исходного уравнения на множитель, содержащий неизвестное, может привести к потере корней. l. Умножение обеих частей на множитель, содержащий неизвестное, может привести к приобретению посторонних корней. l. Возведение в четную степень может привести к появлению посторонних корней.
Найти ошибку в решении уравнения: ОДЗ: х=8 Ответ: 8.
Найти ошибку в решении уравнения: одз: х=0 – не удовлетворяет ОДЗ Ответ: корней нет.
Найти ошибку в решении уравнения x=-3 Ответ: -3.
Тождества, использование которых может привести к потере корней или появлению посторонних корней:
Домашнее задание l Решить уравнения: 1. 2. 3. Какие ошибки могут быть допущены при решении? l Решить системы уравнений из набора: №№ 14; 16; 21 l Выполнить тест «Решение неравенств» на uztest. ru
Скачать презентацию Равносильные и неравносильные преобразования при решении уравнений
Неравносильные преобр уравнений.ppt