Ratios and Proportions CHAPTER 8 Ratios

Ratios and Proportions CHAPTER 8

Ratios • Ratio- Uses division to compare two numbers. • Equivalent ratios- Two ratios are equivalent ratios when they have the same value. 8. 1

Writing a Ratio WORDS NUMBERS • Wins to losses • wins losses • Wins: Losses 18 to 13 18: 13 ALGEBRA A to B, where b is nonzero A B, where B is nonzero A: B where B is nonzero

Writing Ratios in Simplest Form • A water ride lasts 2 • Write hours as minutes so that the units are min. Suppose you the same. wait in line for 1 ½ 1 h+1/2 h=60 min+30 min =90 min hours to ride the • Write the ratio of time water ride. Follow spent in line to time the steps below to spent on the ride. find the ratio of Time in line= 90 time spent in line to Time on ride 2 time spent on the = 45 water ride. 1

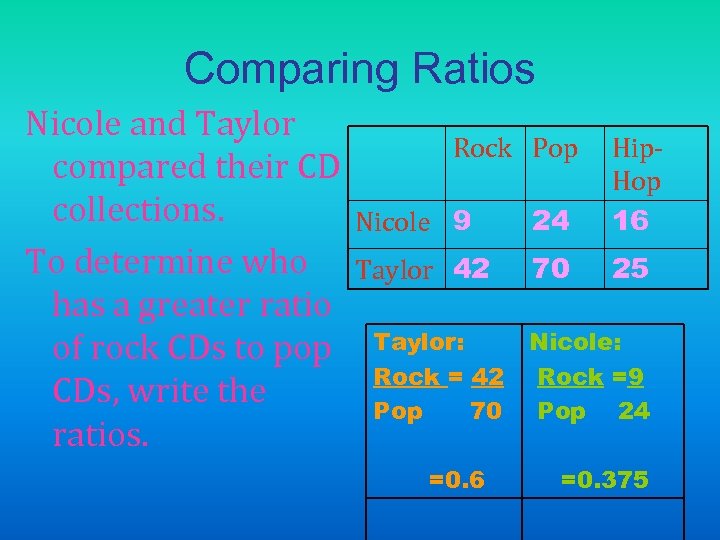Comparing Ratios Nicole and Taylor compared their CD collections. To determine who has a greater ratio of rock CDs to pop CDs, write the ratios. Rock Pop Nicole 9 24 Hip. Hop 16 Taylor 42 70 25 Taylor: Rock = 42 Pop 70 =0. 6 Nicole: Rock =9 Pop 24 =0. 375

Rates 8. 2 • Rate- is a ratio of two quantities measured in different units. • Unit Rate- is a rate that has a denominator of 1 unit rates below are equivalent.

Finding a Unit Rate • During Spring, a sunflower can grow 6 in. in 12 hrs. What is the growth rate of Sunflower in in. per hour? • 6 in. = 6 in. /12 12 h/12 Divide numerator and denominator by 12 = 0. 5 in. simplify 1 h Answer: The growth rate of Sunflower is about 0. 5 in. per hour.

Finding an average speed • An ice skater took 2 min. 30 sec. to complete a 1500 meter race. What was the skater’s average speed? - Divide numerator and denominator by 150. - Simplify • Rewrite the time so that the units are the same. 2 min+30 sec=120 sec+ 30 sec=150 sec Find the average speed 1500 m=1500 m/150 150 sec/150 =10 m 1 sec Answer: the ice skater’s average speed was 10 m per sec.

Writing and solving proportions 8. 4 • Proportion- is an equation that states that two ratios are equivalent.

proportions • Numbers: 3 = 6 5 10 The Proportion is read “ 3 is to 5 as 6 is to 10. ” • Algebra: a = c b d Where b and d are nonzero numbers.

Solving proportions • Solve: 6 = x Write original proportion 10 25 25 x 6 = 25 x x Multiply each side by 25 10 25 150 = X Simplify 10 15=x Simplify Fraction Answer: The solution is 15.

solving proportions using cross products 8. 5 • cross products- in a proportion a/b = c/d where b = 0, the cross products are ad and bc

Cross products property • Words: The cross products of a proportion are equal • Numbers: 3 = 15 4 x 15 = 60 4 20 3 x 20 = 60 • Algebra: If a/b = c/d where b and d are nonzero numbers, then ad = bc.

solving a proportion using cross products • Use the cross products property to solve: 4/8 = 5/d. 1. Write original proportion. 2/1 = 6/d 2. Cross products property. 2 d = 1 x 6 3. Divide each side by 2. 2 d/2 = 1 x 6/2 4. Simplify d = 3

Scale Drawings and Models 8. 6 • Scale drawing- a diagram of an object in which the dimensions are in proportion to the actual dimensions of the object. • Scale- On a scale drawing tells how the drawing’s are related. • Scale model- a model of an object in which the dimensions are in proportion to the actual dimensions of the object.

Finding a Dimension on a Scale Model A scale model of the White House appears Japan. The scale used is 1: 2. The height h of the main building of the White House is 76 ft. Find the height on the Model. 1 = h scale model 2 76 building 1 x 76 = 2 x h Cross products property. 38 = h divide each side by 2.

Vocabulary • Ratio A. Uses division to compare two numbers. B. Two ratios are equivalent ratios when they have the same value.

Vocabulary • Equivalent ratios A. Uses division to compare two numbers. B. Two ratios are equivalent ratios when they have the same value.

Write the ratio of the first number to the second number in three ways. 1. 1, 1 1: 1 1/1 1 to 1

Vocabulary • Rate A. Rate that has a denominator of 1 unit. B. Ratio of two quantities measured in different units.

Vocabulary • Unit rate A. A rate that has a denominator of one unit. B. Is a ratio of two quantities measured in different units.

Match the rate with the equivalent unit rate. • 18 ft 3 sec A. 2. 2 ft/sec B. 4. 5 ft/sec C. 6 ft/sec

Vocabulary • Proportion A. Equation that states that two rates are equivalent. B. Equation that states that two ratios are equivalent.

Use equivalent ratios to solve the proportion • 20 = x 10 2 A. -2 B. 4 C. 2 D. -4

Vocabulary • Cross products A. The cross products of a proportion are equal. B. In a proportion a/b = c/d where b non equal to 0 and d non equal to 0, the cross products are ad and bc

Use the cross products property to solve the proportion. • 8=2 4 n A. -1 B. 2 C. 1 D. -2

Vocabulary • Scale drawing A. Diagram of an object in which the dimensions are in proportion to the actual dimensions of the object B. Tells how the drawing’s dimensions are related.

Vocabulary • Scale A. Tells how the drawing’s dimensions and the actual dimensions are related. B. Model of an object in which the dimensions are in proportion to the actual dimensions of the object.

Vocabulary • Scale model A. Model of an object in which the dimensions are in proportion to the actual dimensions of the object B. Diagram of an object in which the dimensions are in proportion to the actual dimensions of the object

The scale on a map is 1 cm: 25 mi. Find the actual distance in miles for the given length on the map. • 10 cm A. 225 miles B. 250 miles C. 275 miles