Rationality as a Paradigm for Internet Computing Noam

Rationality as a Paradigm for Internet Computing Noam Nisan Hebrew University, Jerusalem Noam Nisan Slide 1 of 27

Contents • The Internet and the new face of computing • Analyzing computing systems in equilibrium • Designing computational mechanisms • A defining problem: Combinatorial auctions Noam Nisan Slide 2 of 27

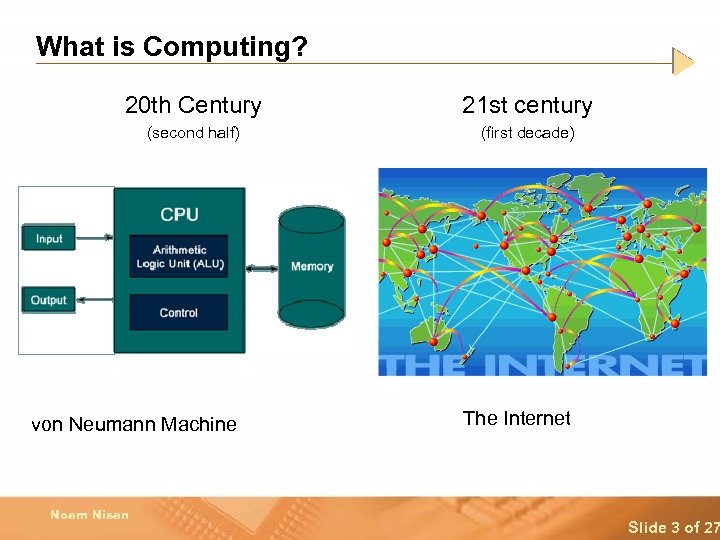What is Computing? 20 th Century 21 st century (second half) (first decade) von Neumann Machine The Internet Noam Nisan Slide 3 of 27

The Internet • Huge dynamic heterogeneous distributed system – “normal distributed CS” • Not centrally owned – different parts owned by different people, firms, or organizations with differing goals – “CS+economics+gametheory”’ Noam Nisan Slide 4 of 27

TCP Retransmission Rule • Transmission Control Protocol Used for most Internet communication § Breaks messages into packets, and assembles the packets back into messages § Handles packet delay/loss § • TCP Retransmission Rule When a packet is lost, decrease transmission rate (by a factor of 2) § Rational: Network is congested – fix it by reducing demand down to capacity § • “Improved” Rule When a packet is lost, start sending each packet twice § Rational: Packets are lost – fix it by increasing the probability that at least one copy of each packet arrives § • Why not? Noam Nisan Slide 5 of 27

Internet Resource Sharing • The vision § everyone connected to the Internet should have access to all resources that are connected to the Internet • Examples: § § § CPU-time Files I/O devices Data Knowledge Humans • Why share? Noam Nisan Slide 6 of 27

Electronic Commerce • How will computers talk business? • Using communication, security software, agents, … • Using standards: XML, . NET, J 2 EE, … and other TLAs • What will they say to each other? • “Book X costs Y” • “Bid X for Y units of stock Z” • “Here’s a complicated offer to you guys: @#$%^ ” Noam Nisan Slide 7 of 27

Internet Computing Protocols • Should take into account § Computational issues: CPU time, communication, robustness, memory, languages, … § Incentive issues: Selfishness, strategies, payments, coalitions, risk, … • Should combine the points of view of Computer Science and of economics • Should apply game theory in a computational context • Rational behavior is more easily assumed from computers than from humans § The strategy is in the software Noam Nisan Slide 8 of 27

At All Protocol Levels … High level (traditional business domain) • • • e. Commerce: e. Stores, auctions, exchanges, supply chains Online Services: games, web-hosting, ASPs Information Resources: music, databases • Computational resources: CPU, disk space, proxies, caching, • Network Infrastructure: routing, admission control, Qo. S Low level (traditional CS domain) Noam Nisan Slide 9 of 27

The Price of Anarchy Papadimitriou • Take a “normal” CS protocol that works well if • • • everyone does what they should…. Say “Oh my god – the participating computers may do whatever they want…” Analyze what happens when “they do whatever they want” Radical departure from CS: “want” utility rationality game-theory equilibrium Aim to prove that things are still not too bad Or else: argue against using on the Internet Noam Nisan Slide 10 of 27

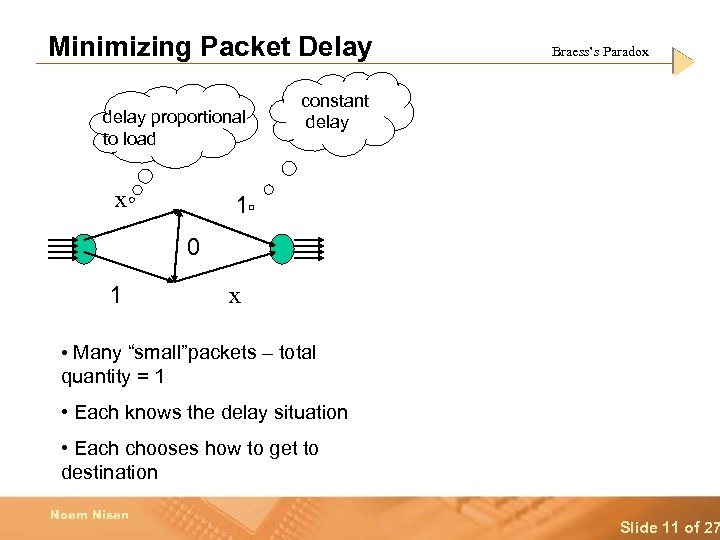Minimizing Packet Delay delay proportional to load x Braess’s Paradox constant delay 1 0 1 x • Many “small”packets – total quantity = 1 • Each knows the delay situation • Each chooses how to get to destination Noam Nisan Slide 11 of 27

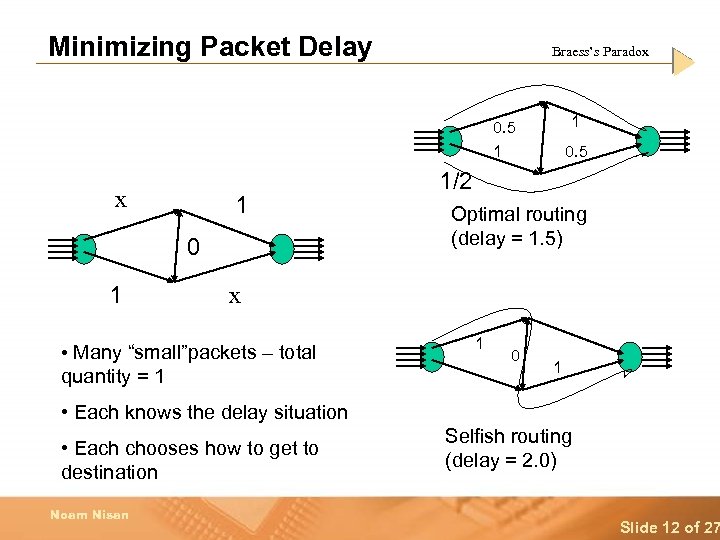Minimizing Packet Delay Braess’s Paradox 1 0. 5 1/2 Optimal routing (delay = 1. 5) x • Many “small”packets – total quantity = 1 1 0 1 • Each knows the delay situation • Each chooses how to get to destination Noam Nisan Selfish routing (delay = 2. 0) Slide 12 of 27

The Price of Anarchy is Low Roughgarden&Tardos Theorem: for all network topologies, for all sets of routing requests, for all delay functions on the links: 1. 2. Noam Nisan If all delays are linear functions, then the previous example is as bad as it gets – the price of anarchy is at most a factor of 4/3 in delay For general delay functions, doubling the edge capacities compensates for selfishness – the price of anarchy is at most a factor of 2 in infrastructure Slide 13 of 27

Algorithmic Mechanism Design Nisan&Ronen • Design the protocols so that they will work well under selfish behavior of participants “work well” – the usual computational optimization goals § “under selfish behavior” – the usual game-theoretic concepts of equilibrium § • Use notions and techniques from the economic field of Mechanism Design § “Inverse game-theory” • Concentrate on “incentive compatibility” (truthfulness) Equilibrium is reached when all players report their private information truthfully § The revelation principle shows that this is without loss of generality § Noam Nisan Slide 14 of 27

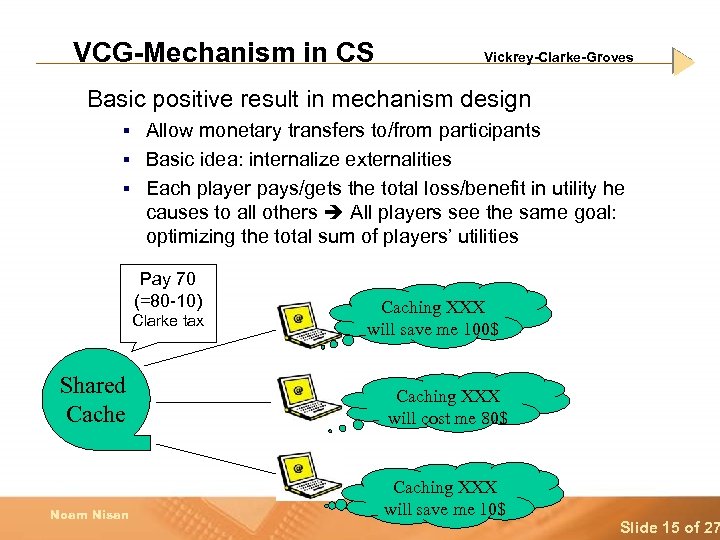VCG-Mechanism in CS Vickrey-Clarke-Groves Basic positive result in mechanism design Allow monetary transfers to/from participants § Basic idea: internalize externalities § Each player pays/gets the total loss/benefit in utility he causes to all others All players see the same goal: optimizing the total sum of players’ utilities § Pay 70 (=80 -10) Clarke tax Caching XXX will save me 100$ Shared Cache Caching XXX will cost me 80$ Noam Nisan Caching XXX will save me 10$ Slide 15 of 27

Beyond Classical Mechanism Design • New domain of problems Parameter-complexity: e. g. structure of network § Brave-new-world: disregard human conventions and biases § • New optimization goals § Not just sum-of-utilities: e. g. make-span in scheduling • New limitations Computational complexity § Distributed implementation § Interaction with usual mechanism design often problematic § • New biases regarding solution concepts Computer scientists don’t like Bayesian analysis: real-world distributions are too different from those in our analysis – worst-case will happen § Computer scientists are happy with approximations: optimality is often too hard § Noam Nisan Slide 16 of 27

A Sampling of Some Recent Results • Selling “digital goods” (unlimited supply) Goldberg&Hartline&Wright A randomized mechanism can approximate monopoly price revenue • Scheduling jobs on “unrelated machines” Nisan&Ronen No better than 2 -approximation for the make-span is possible, but randomized mechanisms can do better • Scheduling jobs on “related machines” Archer&Tardos A polynomial time 3 -approximation mechanism for the make-span • Cost-sharing for multicast transmissions FPS VCG mechanism can be implemented in linear communication • Auctions using a few bits Blumrosen&Nisan An auction with 1 -bit from each player can achieve 98% efficiency Noam Nisan Slide 17 of 27

Combinatorial Auctions • Most mechanism design problems involve resource allocation • The central problem in classical mechanism design is an auction: how to allocate a single indivisible good? Abstracts many resource allocation problems § English auction, Dutch auction, first price sealed-bid auction, … § Gold standard: Vickrey’s 2 nd price auction § • The emerging central problem in algorithmic mechanism design is a combinatorial auction: how to allocate a collection of goods, with complex dependencies between them? Abstracts many complex resource allocation problems § Involves a wide spectrum of computational and game-theoretic issues § Noam Nisan Slide 18 of 27

Combinatorial Auction Problem Definition • N indivisible non-identical items are sold concurrently • k bidders compete for subsets of these items • Each bidder j has a valuation for each set of items: vj(S) = value that j assigns to acquiring the set S § vj is monotonic non-decreasing (“free disposal”) • Objective: Find a partition (S 1…Sk) of {1. . N} that maximizes the social welfare: j vj(Sj). • Means: protocol between bidders and auctioneer • Difficulties: communication, computation, incentives Noam Nisan Slide 19 of 27

Complements and Substitutes • vj() may have complements: vj(S T) > vj(S)+vj(T) for some S and T. § Extreme case: “single-minded bid” -- will only pay for a complete package -- pay p for the set S but pay nothing for anything else • vj() may have substitutes: vj(S T) < vj(S)+vj(T) for some disjoint S and T. § Extreme case: “unit demand bid” -- will pay for at most a single item – the price may depend on the item Noam Nisan Slide 20 of 27

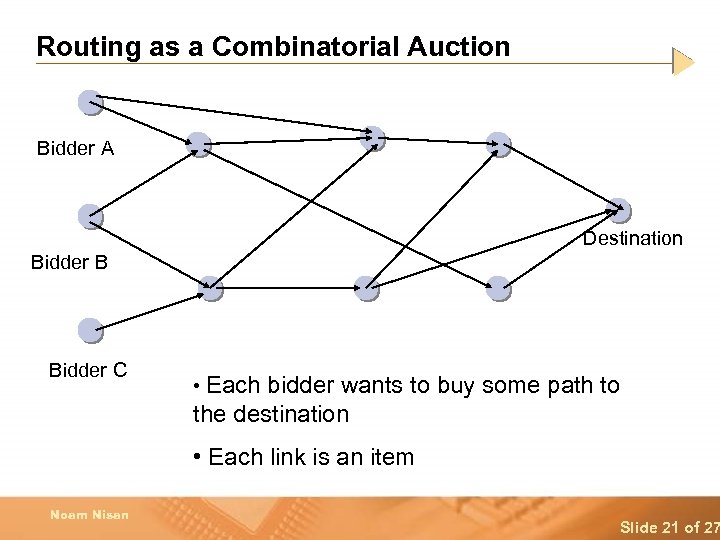Routing as a Combinatorial Auction Bidder A Destination Bidder B Bidder C • Each bidder wants to buy some path to the destination • Each link is an item Noam Nisan Slide 21 of 27

The FCC Spectrum Auctions • The FCC auctions spectrum licenses for many • • geographic regions and various frequency bands These auctions have raised billions of dollars The value of a license to a bidder depends on the other licenses it holds Currently licenses are 3. 1 -3. 2 GHz sold in a simultaneous 3. 2 -3. 3 GHz auction 3. 3 -3. 4 GHz USA Congress mandated 3. 1 -3. 2 GHz that the next spectrum 3. 2 -3. 3 GHz auction be made 3. 1 -3. 2 GHz combinatorial. 3. 2 -3. 3 GHz Noam Nisan 3. 3 -3. 4 GHz Slide 22 of 27

Basic Mechanism Design Approach • Basic Solution § Each bidder sends vj() to auctioneer. Auctioneer finds the partition that maximizes j vj(Sj). § Auctioneer allocates Sj to each bidder j § Auctioneer charges VCG payments – ensures incentive compatibility § • Computational difficulties Bidding: How to send vj()? Requires communication of numbers – impractical § Allocation: How can the auctioneer find an optimal allocation? The problem is computationally intractable (even to approximate well) § Noam Nisan Slide 23 of 27

Bidding Languages • The auction must fix a “language” for representing valuations. All bidders will use that language to express their valuations Language must be expressive: express all reasonable valuations succinctly § Language must be simple: computationally easy to manage valuations (represent, determine allocation, …) § • Proposed languages use: package bids, OR, XOR § (left-sock & right-sock : 5$) OR ( (Red-shirt : 10$) XOR (blue-shirt : 9$)) • Different bidding languages have different power • What should the FCC allow? Noam Nisan Slide 24 of 27

Iterative Auctions Definition: The demand of valuation v at item prices p 1 … pn is the set S that maximizes the benefit: v(S)- i S pi § A Walrasian equilibrium is an allocation S 1…Sm and item prices p 1 … pn such that each Sj is the demand of vj at these prices § Fact: Any Walrasian equilibrium gives an optimal allocation Algorithm: Demange&Gale&Sotomayor initialize prices of all items to 0 § repeat: if an item is demanded by more than one bidder, increase the price a little; until a Walrasian equilibrium is reached § Theorem: This works if valuations are “gross substitutes” Kelso&Crawford Theorem: In general, exponential communication (equivalently, an exponential number of prices) is needed Noam Nisan&Segal Slide 25 of 27

Allocation Algorithms • The allocation problem is computationally intractable • Approaches for overcoming computational difficulty § Solve (or approximate) special tractable cases • Gross substitutes • Sub-modular (2 -approximation) • Linear order on items § Lehmann&Nisan Rothkopf&Pekec&Harstad Heuristics that obtain optimal allocations and run “reasonable fast” • Practical for 100 s of items § Kelso&Crawford CABOB -- Sandholm et al. Heuristics that run quickly and find “reasonably good” solutions • A few % loss for 1000 s of items Zurel&Nisan • Use the usual tools of combinatorial optimization LP relaxation § Branch-and-bound, cutting-planes § Local search § Dynamic programming § Noam Nisan Slide 26 of 27

Incentives vs. Allocation • Challenge: find a mechanism that obtains “reasonably good” allocations and is computationally efficient. • Key problem: Algorithms that find sub-optimal allocations do not yield incentive compatible mechanisms § Attaching VCG payments to sub-optimal algorithms essentially never yields incentive compatibility Nisan&Ronen § The only known incentive compatible mechanisms are VCG; for “complete spaces” with at least 3 possible outcomes only VCG mechanisms exist. Roberts, Green&Laffont • Special case: single minded bidders – have a single valuation parameter and desire a single package § A Computationally efficient incentive compatible mechanism exists Lehmann&Ocallaghan&Shoham • Open problem: Find any non-VCG mechanism for any multi-dimensional valuation space Noam Nisan Slide 27 of 27