РАСТЯЖЕНИЕ И СЖАТИЕ Под растяжением понимается такой вид

РАСТЯЖЕНИЕ И СЖАТИЕ Под растяжением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы, а все прочие внутренние силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.

РАСТЯЖЕНИЕ И СЖАТИЕ

РАСТЯЖЕНИЕ И СЖАТИЕ Естественно предположить, что для однородного стержня внутренние силы распределены по сечению равномерно. Тогда нормальное напряжение для всех точек сечения будет одним и тем же: σ=N/F где F — площадь поперечного сечения.

РАСТЯЖЕНИЕ И СЖАТИЕ Понятно, что высказанное предположение справедливо лишь постольку, поскольку из рассмотрения исключаются особенности конкретно взятого стержня в связи с условиями его закрепления на концах.

РАСТЯЖЕНИЕ И СЖАТИЕ Для этого руководствуются принципом Сен-Венана: особенности приложения внешних сил к растянутому стержню проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня.

РАСТЯЖЕНИЕ И СЖАТИЕ Для нагруженного по концам растянутого однородного стержня напряжения остаются постоянными как по сечению, так и по длине. Такое напряженное состояние называется однородным. При однородном напряженном состоянии все точки тела находятся в одинаковых условиях.

РАСТЯЖЕНИЕ И СЖАТИЕ При растяжении, однако, не всегда возникает однородное напряженное состояние. Так, например, у стержня с переменной площадью поперечного сечения напряжения меняются по длине и напряженное состояние не однородно. То же самое имеет место и для стержня, нагруженного собственным весом.

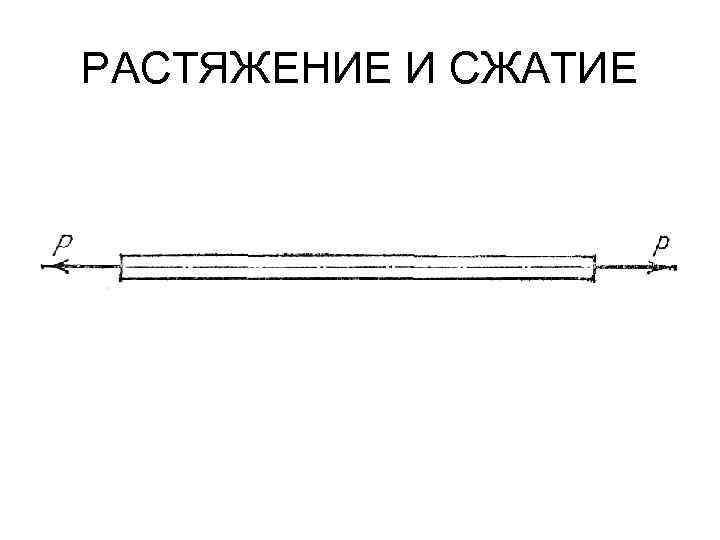
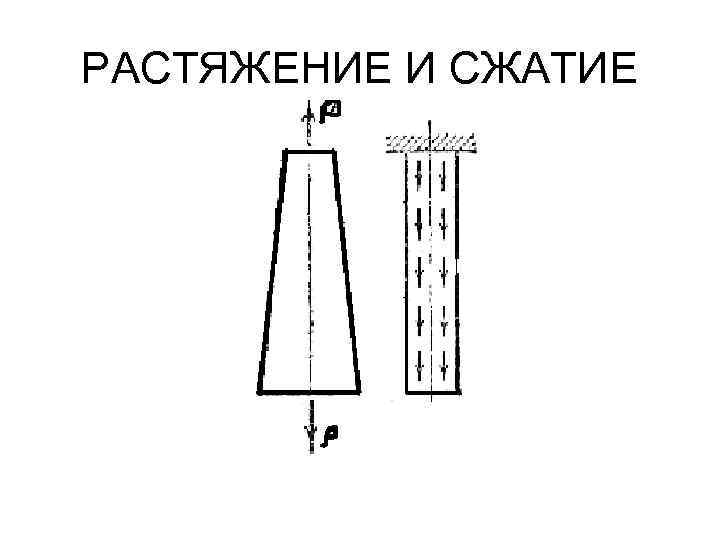
РАСТЯЖЕНИЕ И СЖАТИЕ

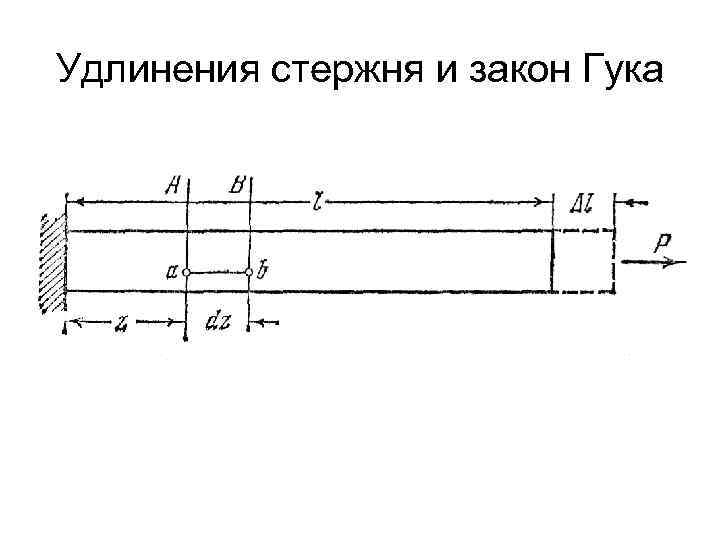
Удлинения стержня и закон Гука Размеры растянутого стержня меняются в зависимости от величины приложенных сил. Если до нагружения стержня его длина была равна L, то после нагружения она станет равной L +Δ L. Величину Δ L называют абсолютным удлинением стержня.

Удлинения стержня и закон Гука

Удлинения стержня и закон Гука Абсолютное удлинение и деформации связаны только с напряжениями, возникающими в стержне. В действительности имеются и другие факторы, влияющие на деформации зависят от температуры и от времени действия нагрузки. Неупругие деформации зависят от «истории» нагружения, т. е. от порядка возрастания и убывания внешних сил.

Удлинения стержня и закон Гука Поскольку у нагруженного стержня напряженное состояние является однородным и все участки растянутого стержня находятся в одинаковых условиях, деформации ε по оси стержня остается одной и той же, равной своему среднему значению по длине L: ε= Δ L / L Эта величина начинается относительным удлинением стержня.

Удлинения стержня и закон Гука Если бы в стержне возникало неоднородное напряженное состояние, деформация в сечении А определялась бы путем предельного перехода к малому участку длиной dz, и тогда ε=Δ(dz)/ dz

Удлинения стержня и закон Гука Вследствие равномерного распределения напряжений можно утверждать, что если концы отрезков до нагружения образуют плоскость, то и после нагружения стержня они образуют плоскость, но смещенную вдоль оси стержня. Это положение может быть взято в основу толкования механизма растяжения и сжатия и трактуется как гипотеза плоских сечений (гипотеза Бернулли).

Удлинения стержня и закон Гука В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между напряжениями и деформациями: =Е ε (1). Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода.

Удлинения стержня и закон Гука Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и , т. е. в мегапаскалях.

Удлинения стержня и закон Гука Вернемся к выражению (1) и заменим в нем на N/F, а ε на ∆(dz)/dz. Тогда получим ∆(dz)=N dz/EF Абсолютное удлинение стержня на длине L будет равно ∆L= 0∫L N dz/EF (2)

Удлинения стержня и закон Гука В том случае, когда стержень нагружен только по концам, нормальная сила N=P не зависит от z. Если, кроме того, стержень имеет постоянные размеры поперечного сечения F, то получаем ∆L=P L /E F

Потенциальная энергия деформации Внешние силы, приложенные к упругому телу, совершают работу. Обозначим ее через А. В результате этой работы накапливается потенциальная энергия деформированного тела U. Кроме того, работа идет на сообщение скорости массе тела, т. е. преобразуется в кинетическую энергию К. Баланс энергий имеет вид A = U+K.

Потенциальная энергия деформации Если нагружение производится медленно, скорость будет весьма малой. Такой процесс нагружения называется статическим. Тело в любой момент времени находится в состоянии равновесия. В этом случае A=U, и работа внешних сил целиком преобразуется в потенциальную энергию деформации.

Потенциальная энергия деформации При разгрузке тела за счет потенциальной энергии производится работа. Таким образом, упругое тело является аккумулятором энергии. Это свойство упругих тел широко используется, например, в различных упругих амортизирующих элементах рессоры, пружины, торсионные валы.

Потенциальная энергия деформации Определим работу А и соответственно потенциальную энергию растянутого стержня. Поскольку на пути ∆L сила Р не остается постоянной, работа, затраченная на растяжение стержня, должна быть определена интегрированием по элементарным участкам пути.

Потенциальная энергия деформации На элементарном перемещении d(∆L ) работа текущей силы Р равна d. A=Pd(∆ L ). Очевидно, работа на перемещении ∆ L численно равна площади треугольника ОВС, т. е. A = U=1/2 Р ∆ L.

Потенциальная энергия деформации

Потенциальная энергия деформации Подставив в полученное для U выражение значение ∆L , найдем U = Р 2 L / 2 Е F

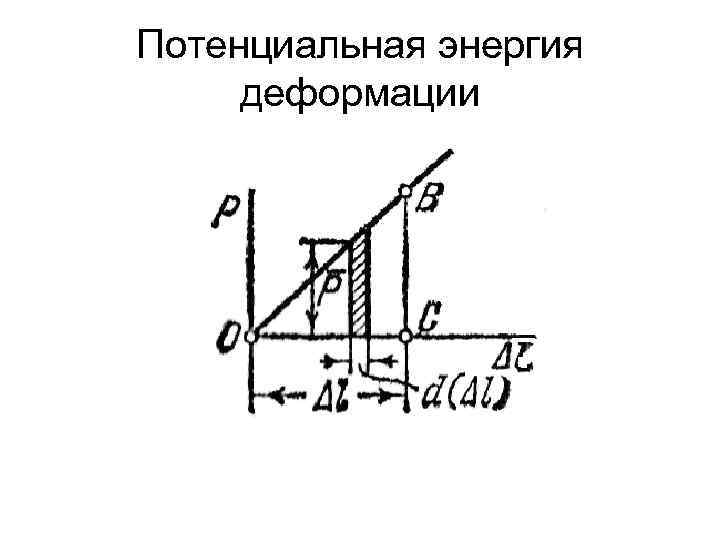
Потенциальная энергия деформации Если нормальная сила N меняется вдоль оси стержня, то потенциальная энергия деформации должна определяться суммированием по участкам dz. Для элементарного участка d. U=N 2 dz/2 Е F а для всего стержня U= o∫L N 2 dz/2 Е F