Растворы электролитов Пропускание тока через раствор электролита сопровождается

Растворы электролитов Пропускание тока через раствор электролита сопровождается разложением растворенного вещества и выделением его составляющих (или их продуктов) на электродах. Т. о. движение заряда в таком растворе сопровождается движением атомов или групп атомов – частей растворенного вещества. Выделение происходит на обоих электродах, в эквивалентных количествах. Законы Фарадея 1 2 Ag H Cu Zn A. м. (г) 108 1 64 65 k (мг/к) 1. 118 0. 01 0. 32 0. 34 1/F=1. 037 10 -5 г/к, F=96500 к Если пропустить 1 F электричества, то выделяется m=(A. м. )/n вещества Элементарный электрический заряд: наименьшее количество электричества, существующее в природе (Гельмгольц) 1

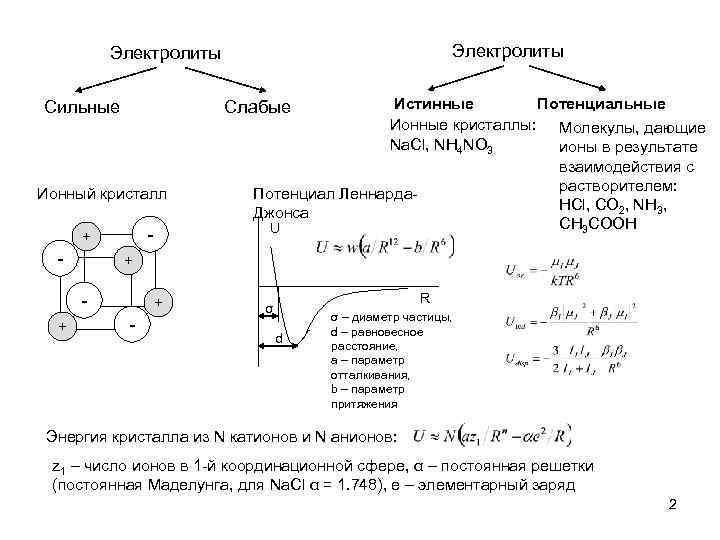Электролиты Сильные Ионный кристалл - + + Истинные Потенциальные Ионные кристаллы: Молекулы, дающие Na. Cl, NH 4 NO 3 ионы в результате взаимодействия с растворителем: Потенциал Леннарда. HCl, CO 2, NH 3, Джонса CH 3 COOH U Слабые + - R σ d σ – диаметр частицы, d – равновесное расстояние, a – параметр отталкивания, b – параметр притяжения Энергия кристалла из N катионов и N анионов: z 1 – число ионов в 1 -й координационной сфере, α – постоянная решетки (постоянная Маделунга, для Na. Cl α = 1. 748), e – элементарный заряд 2

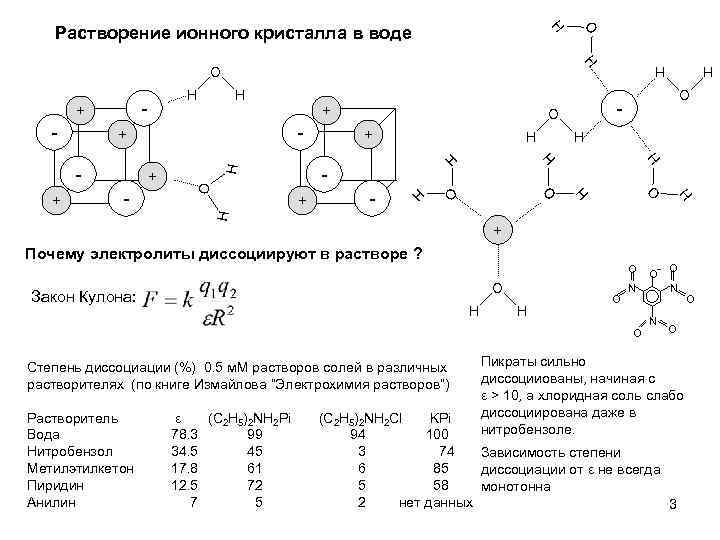- + H H O - H H + O - H + + O - H H + O + Почему электролиты диссоциируют в растворе ? O O Закон Кулона: H H O Степень диссоциации (%) 0. 5 м. М растворов солей в различных растворителях (по книге Измайлова “Электрохимия растворов”) ε (C 2 H 5)2 NH 2 Pi 78. 3 99 34. 5 45 17. 8 61 12. 5 72 7 5 O- N O Растворитель Вода Нитробензол Метилэтилкетон Пиридин Анилин H + O H H H + - H H H O - O H Растворение ионного кристалла в воде O N N O Пикраты сильно диссоцииованы, начиная с ε > 10, а хлоридная соль слабо диссоциирована даже в нитробензоле. (C 2 H 5)2 NH 2 Cl KPi 94 100 3 74 Зависимость степени 6 85 диссоциации от ε не всегда 5 58 монотонна 2 нет данных 3 O

Вывод законов Фарадея из представлений о ионах 2 1 1+2 Масса выделившегося вещества ? – массе одной частицы, умноженной на число частиц: Масса одной частицы: Итак, Произведение силы тока на время – это величина перенесенного заряда, т. е. произведение элементарного заряда, заряда (валентности) иона и числа перенесенных частиц: → Получим объединенный закон Фарадея: 4

Гидратация и сольватация ионов в растворах электролитов Растворение электролитов, как правило, экзотермический процесс, тогда как получение ионов в газовой фазе требует очень больших затрат энергии. Отсюда – представления о гидратации и сольватации: образованием каких-то связей между ионами и молекулами растворителя, что и делает этот процесс энергетически выгодным Пример: Cu. Cl 2 cr Cu 2+, aq + 2 Cl-, aq ΔH= -50 к. Дж/моль Cu. Cl 2 cr Cu 2+, gas + 2 Cl-, gas ΔH= +1986 к. Дж/моль Гидратация катионов – взаимодействие с неподеленными электронными парами кислорода в молекуле воды. Катионы s и p элементов – ион-дипольное взаимодействие, катионы переходных металлов – донорно-акцепторная связь за счет перехода электронов атома кислорода на вакантные связывающие орбитали катионов металлов. Гидратация анионов – за счет образования водородных связей с частичным переходом электронной плотности с аниона на молекулу воды. Сольватация: катионы взаимодействуют с донорными функциональными группами или атомами растворителей, а анионы – с акцепторными. Соответственно, основные (по Льюису) растворители склонны сольватировать катионы, а кислотные – анионы. 5

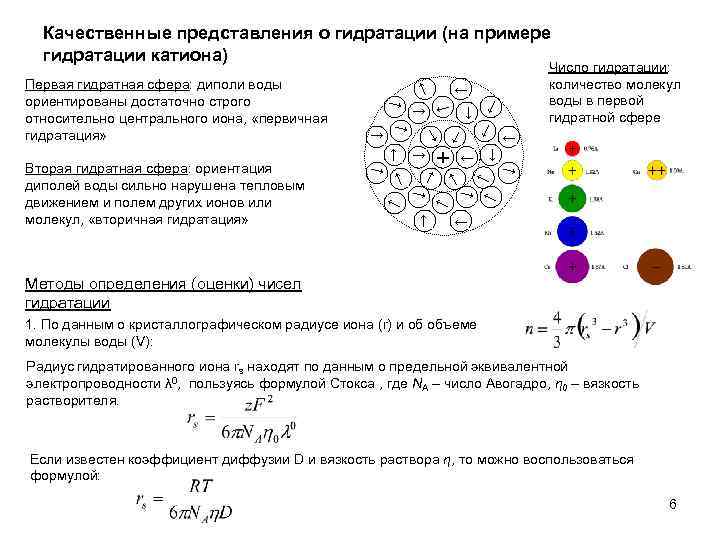Качественные представления о гидратации (на примере гидратации катиона) ← ← ← + ← ← ← ← ← ← Вторая гидратная сфера: ориентация диполей воды сильно нарушена тепловым движением и полем других ионов или молекул, «вторичная гидратация» ← ← Первая гидратная сфера: диполи воды ориентированы достаточно строго относительно центрального иона, «первичная гидратация» Число гидратации: количество молекул воды в первой гидратной сфере ← Методы определения (оценки) чисел гидратации 1. По данным о кристаллографическом радиусе иона (r) и об объеме молекулы воды (V): Радиус гидратированного иона rs находят по данным о предельной эквивалентной электропроводности λ 0, пользуясь формулой Стокса , где NA – число Авогадро, η 0 – вязкость растворителя. Если известен коэффициент диффузии D и вязкость раствора η, то можно воспользоваться формулой: 6

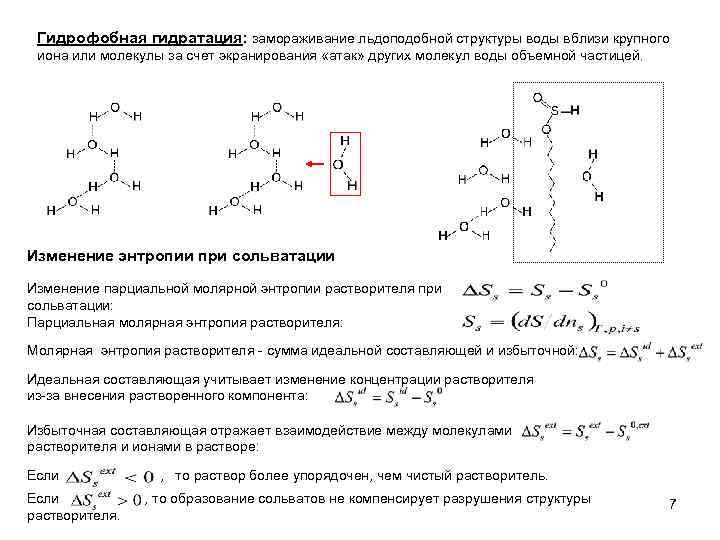Гидрофобная гидратация: замораживание льдоподобной структуры воды вблизи крупного иона или молекулы за счет экранирования «атак» других молекул воды объемной частицей. Изменение энтропии при сольватации Изменение парциальной молярной энтропии растворителя при сольватации: Парциальная молярная энтропия растворителя: Молярная энтропия растворителя - сумма идеальной составляющей и избыточной: Идеальная составляющая учитывает изменение концентрации растворителя из-за внесения растворенного компонента: Избыточная составляющая отражает взаимодействие между молекулами растворителя и ионами в растворе: Если растворителя. , то раствор более упорядочен, чем чистый растворитель. , то образование сольватов не компенсирует разрушения структуры 7

Оценка ионных составляющих свободной энергии и энтальпии сольватации В конденсированных системах при комнатной температуре различие между значениями ΔG и ΔH невелико. Поэтому Строго разделить ΔG и ΔH сольватации электролита на ионные составляющие невозможно. Предполагают, что эти величины одинаковы у гидратов одинаковых радиусов. К этому условию приближается Cs. I ΔHs, Cs. I = -560. 4 к. Дж/моль, принимая ΔHs, Cs = ΔHs, I , для каждого из ионов получим 280. 2 к. Дж/моль. Далее, для солей Cs. X считаем ΔHs, X = ΔHs, Cs. X – ΔHs, Cs , а для иодидов MI ΔHs, M = ΔHs, Cs. I – ΔHs, I. Так получают шкалу ионных энтальпий и свободных энергий гидратации для всех солей цезия и всех иодидов, а затем – вообще для любых электролитов. Слабости этого подхода: 1. Сравнительно произвольный, хотя и логичный выбор «пилотного» электролита – Cs. I; 2. Допущение, что термодинамические функции гидратации пилотных ионов не зависят от природы другого иона в электролите, т. е. гидратация Cs+ одна и та же в растворах всех солей цезия, а гидратация I- - во растворах всех иодидов. Для каких растворов справедливо допущение 2? 8

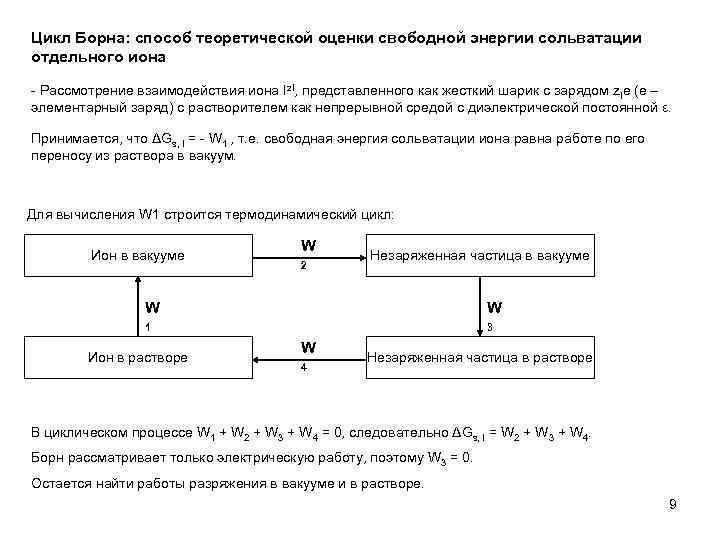Цикл Борна: способ теоретической оценки свободной энергии сольватации отдельного иона - Рассмотрение взаимодействия иона Iz. I, представленного как жесткий шарик с зарядом z. Ie (e – элементарный заряд) с растворителем как непрерывной средой с диэлектрической постоянной ε. Принимается, что ΔGs, I = - W 1 , т. е. свободная энергия сольватации иона равна работе по его переносу из раствора в вакуум. Для вычисления W 1 строится термодинамический цикл: Ион в вакууме W 2 Незаряженная частица в вакууме W W 1 3 Ион в растворе W 4 Незаряженная частица в растворе В циклическом процессе W 1 + W 2 + W 3 + W 4 = 0, следовательно ΔGs, I = W 2 + W 3 + W 4. Борн рассматривает только электрическую работу, поэтому W 3 = 0. Остается найти работы разряжения в вакууме и в растворе. 9

Цикл Борна- продолжение Работа разряжения 1 моля ионов в вакууме определяется электростатическим потенциалом ΦR , зарядом на поверхности иона q и диэлектрической постоянной среды (вакуума) – ε 0: Работа разряжения 1 моля ионов в среде растворителя - аналогично: Комбинируя, получим Уравнение Борна для свободной энергии сольватации: Дифференцируя по температуре, получим выражение для энтропии сольватации: Пользуясь уравнением Гиббса-Гельмгольца, получим для энтальпии сольватации Уравнение Борна-Бьеррума: 10

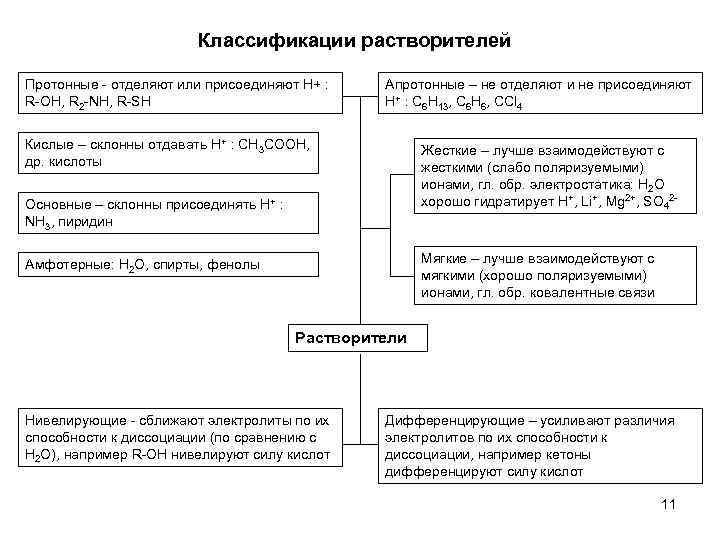Классификации растворителей Протонные - отделяют или присоединяют H+ : R-OH, R 2 -NH, R-SH Апротонные – не отделяют и не присоединяют H+ : C 6 H 13, C 6 H 6, CCl 4 Кислые – склонны отдавать H+ : CH 3 COOH, др. кислоты Жесткие – лучше взаимодействуют с жесткими (слабо поляризуемыми) ионами, гл. обр. электростатика: H 2 O хорошо гидратирует H+, Li+, Mg 2+, SO 42 - Основные – склонны присоединять H+ : NH 3, пиридин Мягкие – лучше взаимодействуют с мягкими (хорошо поляризуемыми) ионами, гл. обр. ковалентные связи Амфотерные: H 2 O, спирты, фенолы Растворители Нивелирующие - сближают электролиты по их способности к диссоциации (по сравнению с H 2 O), например R-OH нивелируют силу кислот Дифференцирующие – усиливают различия электролитов по их способности к диссоциации, например кетоны дифференцируют силу кислот 11

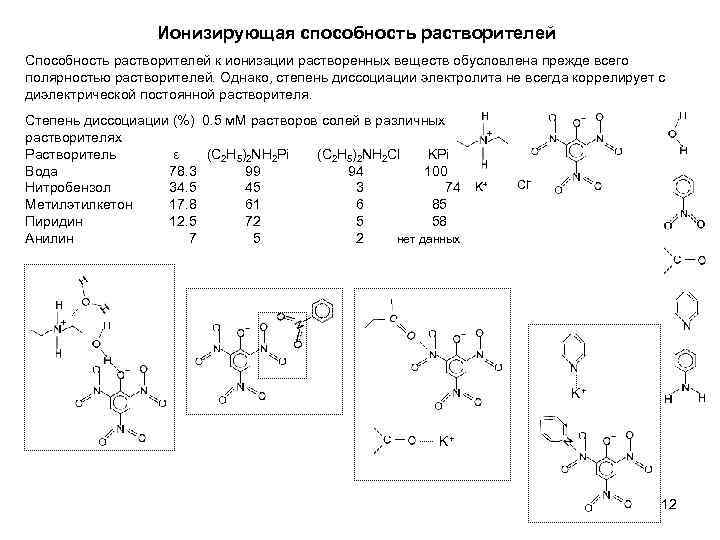Ионизирующая способность растворителей Способность растворителей к ионизации растворенных веществ обусловлена прежде всего полярностью растворителей. Однако, степень диссоциации электролита не всегда коррелирует с диэлектрической постоянной растворителя. Степень диссоциации (%) 0. 5 м. М растворов солей в различных растворителях Растворитель ε (C 2 H 5)2 NH 2 Pi (C 2 H 5)2 NH 2 Cl KPi Вода 78. 3 99 94 100 Нитробензол 34. 5 45 3 74 Метилэтилкетон 17. 8 61 6 85 Пиридин 12. 5 72 5 58 Анилин 7 5 2 нет данных K+ Cl- K+ K+ 12

Активность и концентрация компонента Формальное соотношение активности и концентрации: Концентрация – величина, пропорциональная количеству вещества в единице массы или объема, в этом смысле – относительна, но абсолютна в том смысле, что не является разностной. Концентрация имеет размерность. Активность – величина, связанная со свободной энергией и заданная как функция химического потенциала: Поэтому численное значение активности зависит от выбора стандартного состояния. Активность – безразмерная величина, размерность коэффициента активности обратна размерности концентрации: 13

Особенности термодинамики ионных систем Полные потенциалы – потенциалы, которые включают все виды работы, совершаемой при перемещении массы компонента из одной части системы в другую Примеры: Гравитационно-химический потенциал. Пусть масса i-го компонента dni перемещается вдоль вертикальной оси (т. е. вдоль градиента поля тяготения) на расстояние (h”–h’). Изменение свободной энергии Гиббса составит d. G=(μi”- μi’)dni + Mig(h”-h’)dni. πi = μi + Migh (химическая + механическая работа) Mi – масса, соответствующая dni, g –ускорение свободного падения. Равновесие устанавливается при d. G=0, т. е. πi’= πi” или μi’+Migh’= μi”+Migh” Электрохимический потенциал. Пусть dni ионов сорта i преодолевает скачок электрического потенциала (ψ”- ψ’). Изменение свободной энергии Гиббса составит d. G = (μi”- μi’)dni + zi. F(ψ”- ψ’)dni. μ = μi+zi. Fψ (химическая и электрическая работа) I Равновесие устанавливается при d. G=0, т. е. или , т. е. 14

Активность электролита, средние и ионные активности Пусть электролит диссоциирует по схеме: Раствор: растворитель S и растворенный электролита E. Запишем для них уравнение Гиббса-Дюгема: или С другой стороны, раствор состоит из растворителя и ионов. Для раствора в 1000 г растворителя можем записать: или Моляльные концентрации ионов: Следовательно, т. е. или Стандартное состояние: Для электролита стандартное состояние выбираем так, чтобы Const=1: Отсюда связь активности электролита, средней активности и активностей ионов: Коэффициент активности электролита и ионные коэффициенты активности 15

Методы экспериментального определения коэффициентов активности 1. Методы, использующие данные о химическом потенциале растворителя (например -давлении пара) - основаны на уравнении Гиббса-Дюгема 1. 1. Давление пара растворителя над раствором пропорционально активности растворителя: 1. 2. Изопиестический метод: два раствора нелетучих компонентов приводят в равновесие по растворителю, затем определяют составы обоих растворов. 1. 3. Криоскопический и эбуллиоскопический методы: по изменению температуры замерзания или кипения в сравнении с чистым растворителем 16

2. “Прямые” методы 2. 1. Экстракционный метод: μi(1) = μi(2) – приводят в равновесие растворы в двух несмешивающихся растворителях. Находят коэффициент распределения ki = Ci(1)/Ci(2) при разных значений концентраций. Экстраполируя на предельное разбавление, находят ki 0 – термодинамический коэффициент распределения, ki 0 = ai(1)/ai(2) ki ki 0 Зная и активности компонента в одном из растворителей, можно теперь найти их для другого растворителя. 0 Ci(2) 2. 2. Метод э. д. с. : определяем активность электролита IX в растворе, путем измерения разности потенциалов 2 -х электродов, обратимых, соответственно, к ионам I+ и X- Проблема: все экспериментальные методы дают активность компонента (электролита как целого). Строгих методов измерения активности ионов не существует. Приближение Мак-Иннеса: Приближение Гуггенгейма: концентрации растворов одинаковы 17

Теория сильных электролитов Сильный электролит: вещество, которое полностью диссоциирует при любой его концентрации в растворе Экспериментальные факты в пользу существования сильных электролитов 1. По данным рентгеноструктурного анализа кристаллическая решетка сильного электролита построена из ионов. Если молекулы отсутствуют в кристалле, то тем менее вероятно их появление в растворе, где силы притяжения между ионами уменьшаются в силу высокой диэлектрической проницаемости среды 2. Коэффициенты экстинкции растворов сильных электролитов не зависят от концентрации 3. Молярные теплоты нейтрализации сильных кислот и оснований не зависят от концентрации Термодинамика описывает свойства физико-химических систем с помощью параметров состояния и функций состояния. Некоторые из них можно измерить непосредственно, другие – выразить через измеримые величины изменения в ходе какого-либо процесса. Термодинамика не дает возможности описать эти величины с помощью модельных представлений. В частности, получить теоретически связь между коэффициентами активности и составом раствора можно только из внетермодинамических представлений. 18

Задача: найти способ теоретического расчета электролитных (и ионных !) коэффициентов активности Если нас интересует активность, обратимся к величине химического потенциала. Разность химических потенциалов компонента в интересующем нас состоянии и в стандартном состоянии разобьем на “идеальную” часть и “поправку” Перейдем к соответствующим выражениям для свободной энергии Гиббса: Итак, надо найти выражение для величины ΔGcorr Теория Дебая-Хюккеля Исходные положения: 1. Неидеальность вызвана межчастичными взаимодействиями: ориентационным, индукционным, дисперсионным, а также кулоновским межионным взаимодействием 2. Все перечисленные взаимодействия, кроме кулоновского, заметны на расстояниях в пределах 1 нм, на расстояниях 10 нм и более кулоновское взаимодействие – единственное. (1 моль/л – 1 нм, 10 -3 моль/л -10 нм) Таким образом, мы можем ограничиться рассмотрением только кулоновских взаимодействий, но должны быть готовы к тому, что теория не будет работать при концентрациях свыше 10 -3 моль/л 19

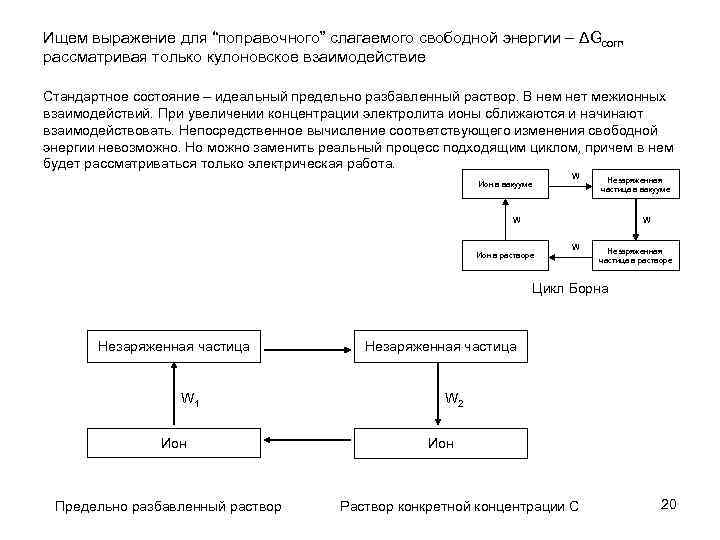Ищем выражение для “поправочного” слагаемого свободной энергии – ΔGcorr, рассматривая только кулоновское взаимодействие Стандартное состояние – идеальный предельно разбавленный раствор. В нем нет межионных взаимодействий. При увеличении концентрации электролита ионы сближаются и начинают взаимодействовать. Непосредственное вычисление соответствующего изменения свободной энергии невозможно. Но можно заменить реальный процесс подходящим циклом, причем в нем будет рассматриваться только электрическая работа. W Ион в вакууме Незаряженная частица в вакууме W W Ион в растворе W Незаряженная частица в растворе Цикл Борна Незаряженная частица W 1 Ион Предельно разбавленный раствор Незаряженная частица W 2 Ион Раствор конкретной концентрации C 20

Работа разряжения иона сорта i в предельно разбавленном растворе Разряжение – изменение заряда иона от его истинной величины zie до 0, т. е. текущее (по ходу процесса) значение заряда q меняется от zie до 0 Для каждого значения q по ходу процесса разряжения справедливо выражение электрического потенциала ψii, создаваемого самим ионом на расстоянии r: Электрическая работа, связанная с изменением заряда на величину dq равна Нас интересует именно работа разряжения данного иона, поэтому за расстояние r мы берем радиус иона: r 0. Тогда работа изменения заряда от zie до 0 равна 21

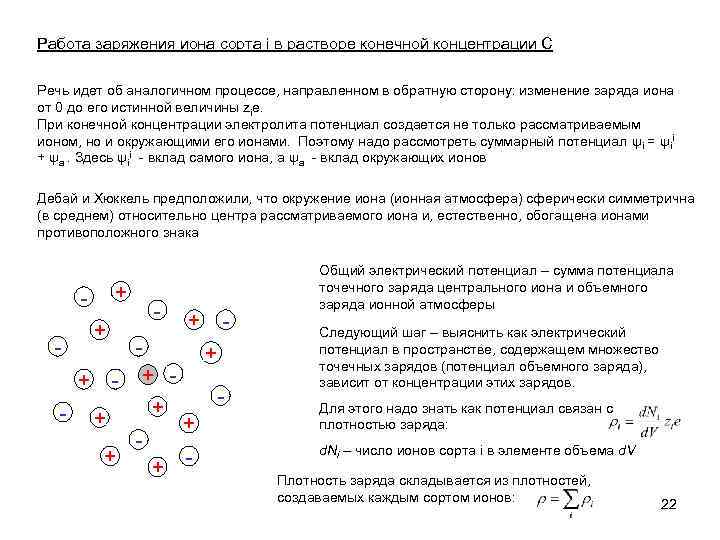Работа заряжения иона сорта i в растворе конечной концентрации C Речь идет об аналогичном процессе, направленном в обратную сторону: изменение заряда иона от 0 до его истинной величины zie. При конечной концентрации электролита потенциал создается не только рассматриваемым ионом, но и окружающими его ионами. Поэтому надо рассмотреть суммарный потенциал ψi = ψii + ψa. Здесь ψii - вклад самого иона, а ψa - вклад окружающих ионов Дебай и Хюккель предположили, что окружение иона (ионная атмосфера) сферически симметрична (в среднем) относительно центра рассматриваемого иона и, естественно, обогащена ионами противоположного знака + + - - + + - Общий электрический потенциал – сумма потенциала точечного заряда центрального иона и объемного заряда ионной атмосферы Следующий шаг – выяснить как электрический потенциал в пространстве, содержащем множество точечных зарядов (потенциал объемного заряда), зависит от концентрации этих зарядов. Для этого надо знать как потенциал связан с плотностью заряда: d. Ni – число ионов сорта i в элементе объема d. V Плотность заряда складывается из плотностей, создаваемых каждым сортом ионов: 22

Связь потенциала объемного заряда с плотностью этого заряда (т. е. с распределением точечных зарядов в объеме) Уравнение Пуассона описывает потенциал любого поля, убывающего по закону 1/r 2 в трехмерном пространстве, при условии гладкой функции распределения частиц, создающих поле Уравнение Пуассона: - + + ++ - + + - - Усреднение по времени делает уравнение Пуассона применимым к реальной ситуации В качестве среднего по времени распределения в теории Дебая -Хюккеля используется распределение Больцмана (барометрическая формула) + Учтем, что и Получим “Основное” уравнение теории Дебая-Хюккеля: Разложим экспоненту в ряд и, считая 2 -мя первыми членами. Получим: , ограничимся только Последнее равенство - в силу электронейтральности: e -x = 1 - x + x 2 x 3 - +. . . 2! 3! 23

Вернемся к уравнению Пуассона, причем оператор Лапласа запишем в полярных координатах, т. к. считаем систему ион + ионная атмосфера центральносимметричной: Т. е. Общее решение имеет вид: α и β – константы интегрирования. Ищем их из граничных условий На бесконечном расстоянии от иона (r → ∞ ) нет поля. Т. е. при r → ∞ д. б. ψ → 0. Первое слагаемое при r → ∞ обращается в 0 при любых α. Чтобы вся сумма обратилась в 0 требуется β=0. Таким образом, Для определения константы α разложим и эту экспоненту в ряд, ограничиваясь 2 -мя первыми членами: Поскольку , то при предельном разбавлении эта величина (χ) обращается в 0. Соответственно, в предельно разбавленном растворе . Отсюда 24

Таким образом, результирующий потенциал в системе ион – ионная атмосфера может быть записан как Здесь Ионную атмосферу можно заменить зарядом, равным по величине заряду центрального иона, противоположным ему по знаку и равномерно распределенным по сфере радиуса r. D = χ-1. Величина r. D - эффективный радиус ионной атмосферы или Дебаевский радиус. Для плоского случая (двойной электрический слой) аналог этой величины – Дебаевская длина: эффективная толщина диффузной части двойного электрического слоя (теория Гуи-Чапмена). Дебаевский радиус: Для 1: 1 электролита в воде при 25 о. С r. D=2 C-1/2 A, при 0. 01 M – r. D=20 A. Теперь получим работу возвращения заряда на ион в растворе конечной концентрации Здесь r 0 т. к. речь о заряжении иона радиусом r 0 25

Для полной электрической работы, связанной с перемещением иона сорта i из предельно разбавленного раствора в раствор конечной концентрации (т. е. работы создания ионной атмосферы): Для всех ионов электролита, присутствующих в объеме V, общая электрическая работа составит Теперь вернемся к исходной идее: поправка на неидеальнность должна отражать только электростатическое взаимодействие, тогда Введем обозначение . В водных р-рах при 25 0 С А~0. 509 Мы получили предельный закон (первое приближение) теории Дебая-Хюккеля: 26

Более точные выражения теории Дебая-Хюккеля Поправка Хюккеля: учет объема самих ионов Интегрирование по всему объему раствора разумно проводить только тогда, когда объем, занимаемый ионами пренебрежимо мал по сравнению с общим объемом, т. е. только для разбавленных растворов (в пределах 0. 001 М). В более концентрированных надо иметь в виду, что ионы могут занять заметную долю объема. С другой стороны, расстояние между центрами ионов не может быть меньше, чем сумма их радиусов. Отсюда - второе приближение теории Дебая-Хюккеля: Исключаем объем центрального иона, т. е. интегрируем не от 0, а от r=a. Величина a – эффективный радиус иона (радиус Киеланда). Тогда константа интегрирования В результате получим , . В водных растворах при 25 0 С B~0. 329 Значения параметра a подбирают эмпирически! Уравнение Дэвис (3 -е приближение теории Дебая-Хюккеля): учет локального изменения диэлектрической постоянной вблизи иона (работает до 0. 1 М растворов, в т. ч. Ca. Cl 2): 27

Более современные теории Теория Робинсона-Стокса – учет расхода растворителя на сольватацию ионов Здесь φs – осмотический коэффициент растворителя, h – число гидратации, ν – количество ионов данного вида в одной молекуле электролита, ns – число молей растворителя в 1 -молярном растворе электролита Теория Питцера: ионы представлены как жесткие сферы, а не как точечные заряды. Т. е. не просто учтен их объем, а учтено отталкивание на близких расстояниях Параметры C и D эмпирические 28

Перенос электрического заряда в растворах электролитов Способы (виды) переноса: конвекция, диффузия, (электро)миграция Конвекция: перенос объема раствора, например – из-за перемешивания Диффузия: перенос электролита в объеме раствора под действием градиента химического потенциала Электромиграция: перенос электролита в объеме раствора под суммарным действием градиентов химического потенциала и внешнего электрического поля Сопротивление Электропроводность Удельная электропроводность: электропроводность объема материала (твердого или жидкого), заключенного в кубике с ребром 1 см, помещенном между двумя электродами большой площади Удельная электропроводность 1 см Вещество Серебро Алюминий Уголь Na. Cl (750 0 C) H 2 SO 4 30% KCl 1 M H 2 O κ (Ом-1 см-1) 6. 2· 105 3. 6· 105 2· 105 3. 4 0. 74 9. 8· 10 -2 5. 5· 10 -8 29

Основное понятие, применяемое при описании процессов переноса вещества, теплоты, электрического заряда, и т. д. – плотность потока. Вектор! Плотность потока частиц сорта i: число частиц этого сорта, пересекающих площадку единичной площади, расположенную перпендикулярно направлению движения частиц, за 1 единицу времени Ji – поток частиц сорта i, двигающихся со скоростью Vi относительно системы отсчета, которая движется со скоростью Vref Кристаллы: система отсчета – кристаллическая решетка Растворы: разные системы отсчета Характеристическая система Гитторфа: Vref – средняя скорость движения частиц растворителя Поток в системе Гитторфа Характеристическая система Фика: Vr = W – средняя скорость движения всего объема раствора, в котором происходит перенос. Удобство системы Фика: если нет конвекции, т. е. раствор покоится относительно наблюдателя, то Vref = W = 0 Ci – концентрация, vi – парциальный молярный объем частиц сорта i Поток в системе Фика 30

Речь идет о движении только вдоль оси x, символ вектора в дальнейшем не применяем + Катод Анод x Плотность электрического тока: Плотность электрического тока не зависит от выбора характеристической системы отсчета! Число переноса ионов сорта i В разбавленных растворах числа переноса по Гитторфу и по Фику совпадают, но в концентрированных могут заметно различаться В любой системе отсчета 31

Подвижность иона Пусть система однородна (нет градиентов) даже по оси x. Тогда никакого направленного переноса не будет, только хаотичное тепловое движение частиц x Наложим внешнее электрическое поле с напряженностью На частицы действует постоянная ускоряющая сила напряженности электрического поля, и тормозящая сила трения , пропорциональная , пропорциональная скорости движения частицы относительно тормозящей среды в текущий момент времени t. В некий момент времени t = τ достигнутая частицей скорость порождает такую тормозящую силу, которая компенсирует действие ускоряющей: Начиная с этого момента t = τ частица движется с постоянной скоростью Vi – Vsolv = Vi, τ – Vsolv = ui - электрическая подвижность иона IZi Тогда для парциальной плотности тока и общей плотности тока получим и 32

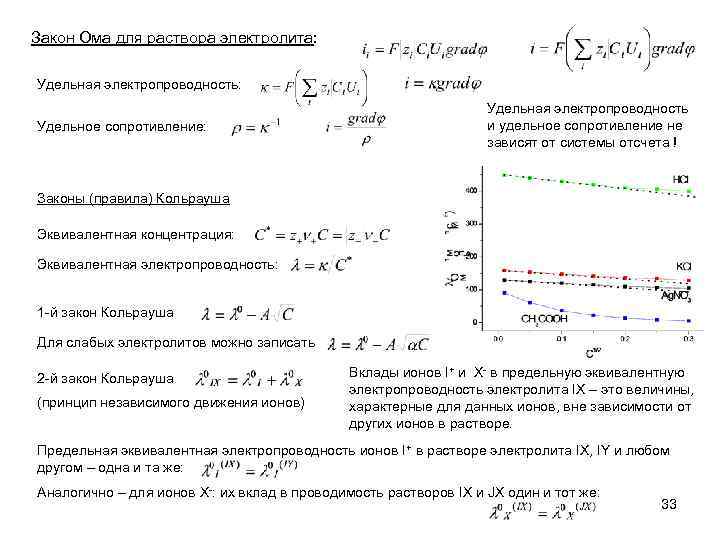Закон Ома для раствора электролита: Удельная электропроводность: Удельное сопротивление: Удельная электропроводность и удельное сопротивление не зависят от системы отсчета ! Законы (правила) Кольрауша Эквивалентная концентрация: Эквивалентная электропроводность: 1 -й закон Кольрауша Для слабых электролитов можно записать 2 -й закон Кольрауша (принцип независимого движения ионов) Вклады ионов I+ и X- в предельную эквивалентную электропроводность электролита IX – это величины, характерные для данных ионов, вне зависимости от других ионов в растворе. Предельная эквивалентная электропроводность ионов I+ в растворе электролита IX, IY и любом другом – одна и та же: Аналогично – для ионов X-: их вклад в проводимость растворов IX и JX один и тот же: 33

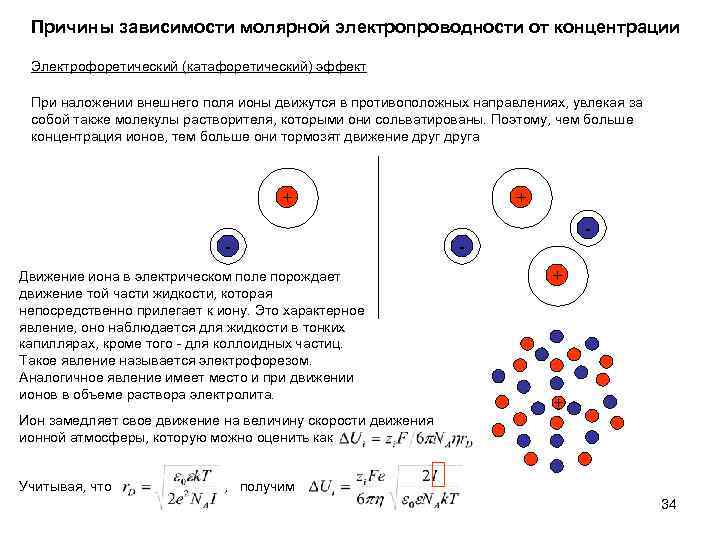Причины зависимости молярной электропроводности от концентрации Электрофоретический (катафоретический) эффект При наложении внешнего поля ионы движутся в противоположных направлениях, увлекая за собой также молекулы растворителя, которыми они сольватированы. Поэтому, чем больше концентрация ионов, тем больше они тормозят движение друга + Движение иона в электрическом поле порождает движение той части жидкости, которая непосредственно прилегает к иону. Это характерное явление, оно наблюдается для жидкости в тонких капиллярах, кроме того - для коллоидных частиц. Такое явление называется электрофорезом. Аналогичное явление имеет место и при движении ионов в объеме раствора электролита. Ион замедляет свое движение на величину скорости движения ионной атмосферы, которую можно оценить как Учитывая, что + - + + , получим 34

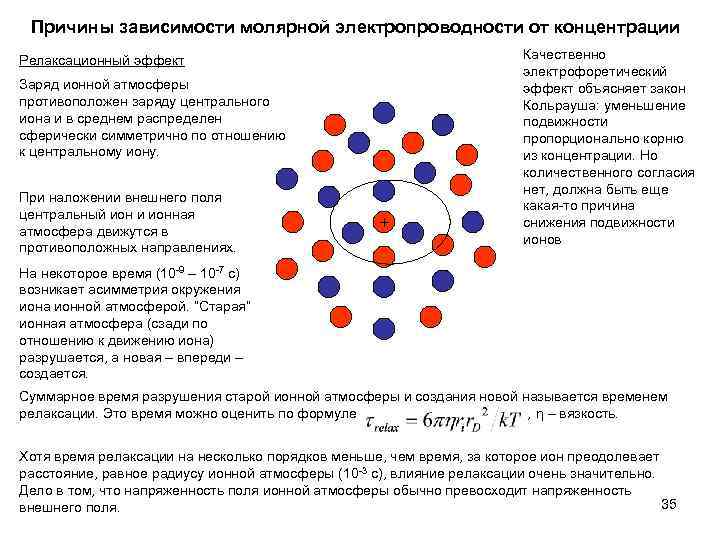Причины зависимости молярной электропроводности от концентрации Релаксационный эффект Заряд ионной атмосферы противоположен заряду центрального иона и в среднем распределен сферически симметрично по отношению к центральному иону. При наложении внешнего поля центральный ион и ионная атмосфера движутся в противоположных направлениях. + Качественно электрофоретический эффект объясняет закон Кольрауша: уменьшение подвижности пропорционально корню из концентрации. Но количественного согласия нет, должна быть еще какая-то причина снижения подвижности ионов На некоторое время (10 -9 – 10 -7 с) возникает асимметрия окружения иона ионной атмосферой. “Старая” ионная атмосфера (сзади по отношению к движению иона) разрушается, а новая – впереди – создается. Суммарное время разрушения старой ионной атмосферы и создания новой называется временем релаксации. Это время можно оценить по формуле , η – вязкость. Хотя время релаксации на несколько порядков меньше, чем время, за которое ион преодолевает расстояние, равное радиусу ионной атмосферы (10 -3 с), влияние релаксации очень значительно. Дело в том, что напряженность поля ионной атмосферы обычно превосходит напряженность 35 внешнего поля.

Теория электропроводности Онзагера Теория Онзагера учитывает межионные электростатические взаимодействия примерно также, как они учтены в теории Дебая-Хюккеля, а потоки всех частиц описываются с помощью уравнений гидродинамики. Учитывается, что в результате электрофоретического эффекта подвижность иона уменьшается (по сравнению с величиной в предельно разбавленном растворе) Кроме того, на внешнее поле Eex накладывается релаксационное поле ΔE: В сильно разбавленном растворе одного электролита IX: где , В результате Онзагер получил для эквивалентной электропроводности выражение: Если и , то получим закон Кольрауша: 36

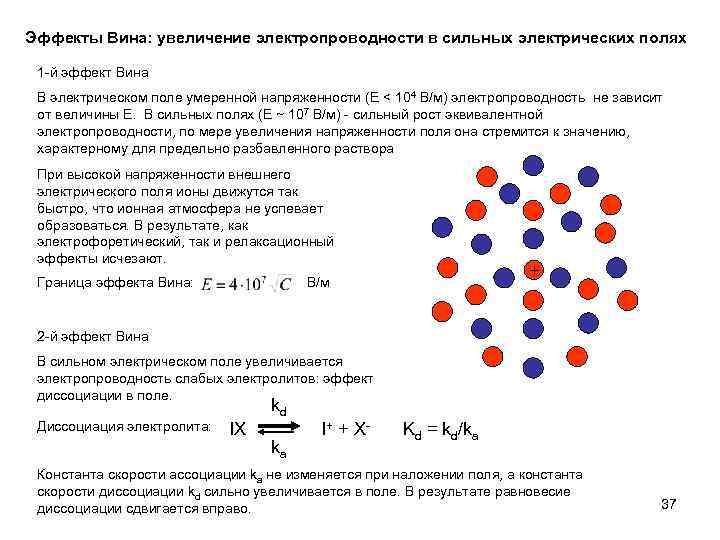Эффекты Вина: увеличение электропроводности в сильных электрических полях 1 -й эффект Вина В электрическом поле умеренной напряженности (E < 104 В/м) электропроводность не зависит от величины E. В сильных полях (E ~ 107 В/м) - сильный рост эквивалентной электропроводности, по мере увеличения напряженности поля она стремится к значению, характерному для предельно разбавленного раствора При высокой напряженности внешнего электрического поля ионы движутся так быстро, что ионная атмосфера не успевает образоваться. В результате, как электрофоретический, так и релаксационный эффекты исчезают. Граница эффекта Вина: + В/м 2 -й эффект Вина В сильном электрическом поле увеличивается электропроводность слабых электролитов: эффект диссоциации в поле. kd Диссоциация электролита: IX ka I + + X- Kd = kd/ka Константа скорости ассоциации ka не изменяется при наложении поля, а константа скорости диссоциации kd сильно увеличивается в поле. В результате равновесие диссоциации сдвигается вправо. 37

Эффект Дебая-Фалькенгагена: увеличение электропроводности в переменном электрическом поле Исходя из идеи ионной атмосферы, Дебай и Фалькенгаген предсказали, что эффект асимметрии (релаксационный эффект) должен исчезнуть, если вместо постоянного электрического поля приложить переменное поле высокой частоты. + Действительно, при частотах порядка 1 МГц, когда период колебаний поля соизмерим со временем релаксации наблюдается заметное увеличение электропроводности Даже малые (и периодические) колебания ионов вызывают колебания их сольватных оболочек. Поэтому электрофоретический эффект сохраняется также и в переменном электрическом поле В переменном поле исчезает только релаксационный эффект, а электрофоретический остается, поэтому эквивалентная электропроводность в переменном поле не достигает значений, характерных для предельно разбавленных растворов 38

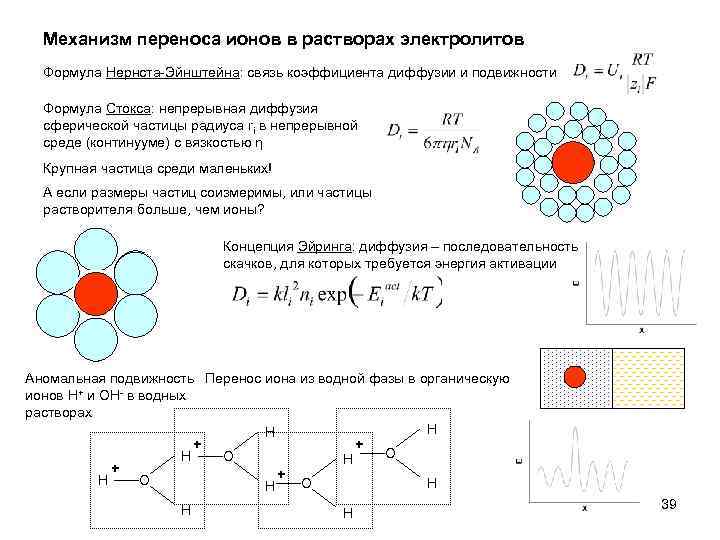Механизм переноса ионов в растворах электролитов Формула Нернста-Эйнштейна: связь коэффициента диффузии и подвижности Формула Стокса: непрерывная диффузия сферической частицы радиуса ri в непрерывной среде (континууме) с вязкостью η Крупная частица среди маленьких! А если размеры частиц соизмеримы, или частицы растворителя больше, чем ионы? Концепция Эйринга: диффузия – последовательность скачков, для которых требуется энергия активации Аномальная подвижность Перенос иона из водной фазы в органическую ионов H+ и OH- в водных растворах H H + + O H + + H O O H H 39

Правило Вальдена-Писаржевского Формула Стокса Водные растворы уксусной кислоты: t, 0 C 0 25 60 100 150 λ 0 CH 3 COOη 0. 366 0. 368 0. 369 В отношении постоянства произведения Diη при разных температурах (в одном растворителе) правило Вальдена-Писаржевского выполняется очень хорошо. В отношении разных растворителей – выполняется редко, хотя при отсутствии данных о коэффициентах диффузии или о вязкости этим правилом пользуются для приблизительных оценок. Электропроводность неводных растворов Как правило, электропроводность неводных растворов значительно ниже, чем водных. Одна из причин низкой проводимости неводных растворов – вязкость растворителей. Но главная – низкая полярность и, соответственно – низкая степень диссоциации. Предельные подвижности ионов в различных растворителях 25 0 С H 2 O Met. OH Et. OH OAc Ph. NO 3 H+ 349. 8 143 59. 5 88. 0 23 Na+ 50. 1 45. 2 18. 7 80. 0 17. 2 K+ 73. 5 52. 4 22. 0 82. 0 19. 2 Cl 76. 4 52. 9 24. 3 111. 0 17. 3 OH 197. 6 53. 0 22. 5 - Cl. O 467. 3 70. 9 33. 8 117. 0 19. 9 Высокая подвижность ионов водорода сохраняется в спиртах: H+ + R-OH → R-OH-H+, а высокая подвижность гидроксила – только в воде, что подтверждает эстафетный механизм подвижности H+ и OH-. Соотношение подвижностей ионов сильно меняется от одного растворителя к 40 другому.

Почему правило Вальдена-Писаржевского не выполняется в смысле постоянства Diη при переходе от одного растворителя к другому? В разных растворителях ионы сольватированы по-разному. Если измерить коэффициент диффузии и вязкость, то можно вычислить Стоксовский радиус иона: Соотношение между Стоксовским ri и кристаллографическим ri, C радиусами ri, C (A) ri/ri, C 2. 04 3. 47 1. 70 N(C 2 H 5)4+ 2. 81 4. 00 1. 42 N(C 3 H 7)4+ 3. 92 4. 52 1. 15 N(C 4 H 6)4+ 4. 71 4. 94 1. 05 N(C 5 H 11)4+ 5. 25 5. 29 1. 01 N(CH 3)4+ Для крупных, слабосольватированных ионов характерно совпадение Стоксовских и кристаллографических радиусов. Для них и правило Вальдена-Писаржевского выполняется как для температурной зависимости, так и для перехода от одного растворителя к другому. Различие между Стоксовским и кристаллографическим радиусами позволяет оценить число молекул растворителя в сольватной оболочке иона Аномальная электропроводность: экстремумы на зависимости λ от концентрации Пример: растворы Ag. NO 3 В крепких растворах диссоциация димеров: [Ag. NO 3]2 → Ag(NO 3)2 - + Ag+ При умеренных концентрациях димеров нет, а сам Ag. NO 3 диссоциирован слабо: проводимость снижается При разбавлении увеличивается диссоциация Ag. NO 3 → Ag+ + NO 341

Кислотность водных и неводных растворов Шкала p. H для водных растворов Ag│Ag. Cl, буфер, KCl (m) │H 2, Pt Буфер Фталатный Фосфатный Боратный Д-Х 4. 002 6. 858 9. 177 γ± 4. 011 6. 873 9. 180 Используют ГЯ без жидкостного соединения, чтобы избежать трудностей с диффузионным потенциалом Измеряют э. д. с. при разных значениях m. Cl и экстраполируют на m. Cl = 0 (γCl = 1). По ходу построения, γCl вычисляют по теории Дебая. Хюккеля или принимают γCl = γ±KCl Построить шкалу p. H водных растворов удается только путем внесения внетермодинамических допущений. Но результаты внесения различных допущений оказываются очень близкими друг к другу Шкала p. H для неводных растворов (? ) 1 aq 1 1 org aq 2 2 aq 2 org Построить единую согласованную шкалу p. H для разных растворителей не удается ! 42

Функции кислотности Аррениус: кислота (HA) – вещество, которое в водном растворе отщепляет ион водорода основание (BOH) –вещество, которое в водном растворе отщепляет ион гидроксила HA ↔ H+ + ABOH ↔ B+ + OHБренстед: кислота (A, BH) – это вещество, способное отщеплять протон, основание (B) – это вещество, способное присоединять протон Az. A ↔ H+ + Bz. A-1 + H+ ↔ Az. A HCl ↔ H+ + Cl. NH 3 + H+ ↔ NH 4+ Важно: необходимы 2 протолитические системы, например A 1 + B 2 ↔ B 1 + A 2 Льюис: кислота (A) – это вещество, способное быть акцептором электронов, основание (B) – это вещество, способное быть донором электронов. Сам ион H+ - кислота Льюиса, реакции – это вытеснение одного основания другим: AB 1 + B 2 ↔ AB 2 + B 1 По Льюису для реакции необходимы 2 основания. Гаммет: для сопоставления кислотности растворов в разных растворителях можно использовать цветные индикаторы (B, BH), концентрации которых малы, поэтому внесение индикатора не влияет на кислотность раствора. Функция кислотности Гаммета (нитроанилины, B, BH+) Считается, что γB/γBH = Const для всех индикаторов во всех растворителях. Для этого химическая структура индикаторов д. б. близкой, а концентрации - маленькими Для индикаторов типа CH ↔ C- + H+ Для индикаторов типа DH 2+ ↔ D+ + H+ 43

Расплавы солей В расплавах в значительной мере сохраняется квазикристаллический порядок чередования ионов различных знаков – как в кристаллической решетке. Но в силу высокой температуры ионы в расплавах имеют высокую кинетическую энергию. Поэтому можно предполагать высокую степень диссоциации в расплавах. Вместе с тем, электропроводность их не так велика, как можно было бы ожидать при такой концентрации зарядов в единице объема и высокой степени диссоциации. Электропроводность расплавов обусловлена дефектами структуры, которых намного больше, чем в твердых солях. Сложные закономерности чисел переноса Удельная электропроводность Вещество Серебро Na. Cl (750 0 C) Li. F (905 0 C) Al. Cl 3 (200 0 C) H 2 SO 4 30% KCl 1 M H 2 O KCl – Mg. Cl 2 (1: 1) κ (Ом-1 см-1) 6. 2· 105 3. 4 20. 3 5. 6· 10 -8 0. 74 9. 8· 10 -2 5. 5· 10 -8 t. K = 0. 7, t. Mg = 0. 14, t. Cl = 0. 16 KCl – Mg. Cl 2 (2: 1) t. K = 0. 8, t. Mg = 0. 0, t. Cl = 0. 20 Расплавные источники тока Анод: металлический Li, Ca (!) Катод: Ca. Cr. O 4, Cu. O, Fe 2 O 3, WO 3 V ~ 3 В, i ~ 103 A/м 2 (!) Li. Cl - KCl 10 – 15 лет хранения в холодном виде 44

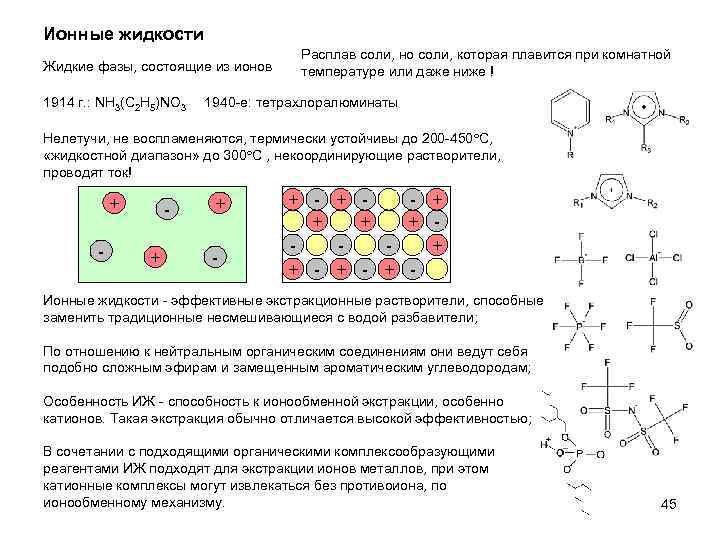Ионные жидкости Жидкие фазы, состоящие из ионов 1914 г. : NH 3(C 2 H 5)NO 3 Расплав соли, но соли, которая плавится при комнатной температуре или даже ниже ! 1940 -e: тетрахлоралюминаты Нелетучи, не воспламеняются, термически устойчивы до 200 -450 С, «жидкостной диапазон» до 300 С , некоординирующие растворители, проводят ток! + - + - + + + + - + - Ионные жидкости - эффективные экстракционные растворители, способные заменить традиционные несмешивающиеся с водой разбавители; По отношению к нейтральным органическим соединениям они ведут себя подобно сложным эфирам и замещенным ароматическим углеводородам; Особенность ИЖ - способность к ионообменной экстракции, особенно катионов. Такая экстракция обычно отличается высокой эффективностью; В сочетании с подходящими органическими комплексообразующими реагентами ИЖ подходят для экстракции ионов металлов, при этом катионные комплексы могут извлекаться без противоиона, по ионообменному механизму. 45