Рассмотрим расчет надежности по более сложным блок-схемам когда

Рассмотрим расчет надежности по более сложным блок-схемам, когда нет возможности выделить параллельные и последовательные участки. На рис. приведена надежностная блоксхема системы с функциональным резервированием.

• Основными являются блоки 1 и 3. Блоки 2 и 4 их дублируют. Блок 5 одновременно резервирует часть функций блоков 3 и 4.

• Получается мостиковая схема, в которой нет возможности выделить параллельное и последовательное соединение. В таких случаях прибегают к логико-вероятностному методу расчета надежности.

• Применительно к схеме, изображенной на рис. рассмотрим основные этапы расчета надежности системы логиковероятностным методом.

• 1. Словесная формулировка условий работоспособности объекта. Объект исправен, если исправны блоки 1 и 3 или блоки 2 и 4, или блоки 1, 5 и 4, или блоки 2, 5 и 3.

• 2. Составление логической функции работоспособности:

• 3. Минимизация и упрощение логической функции. • Функции стараются привести к виду, чтобы в каждую функцию входило не больше двух членов. Для этого можно воспользоваться разложением логической функции по переменной С на 2 части:

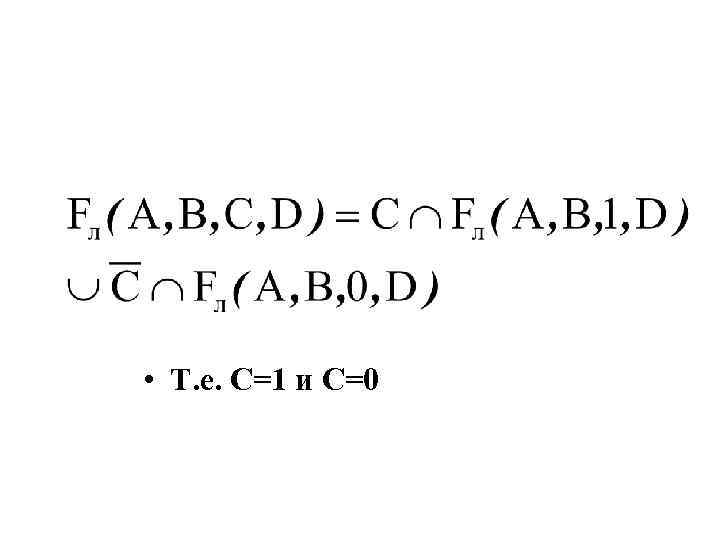
• Т. е. C=1 и C=0

тогда

4. Арифметизация булевой функции. • Правила арифметизации следующие:

Следовательно:

5. Замена событий их вероятностями: • Pc = P 5∙(P 1+P 2 -P 1∙P 2)(P 3+P 4 -P 3 P 4)+(1 -P 5)∙(P 1∙P 3+P 2∙P 4 -P 1∙P 3∙P 2∙P 4) • -P 5∙(1 -P 5)∙(P 1+P 2 -P 2∙P 1)∙(P 3+P 4 P 3∙P 4)∙(P 1∙P 3+P 2∙P 4 -P 1∙P 2∙P 3∙P 4).

6. Расчет надежности. • Пусть Р 1=Р 2=0. 9; РЗ=Р 4=Р 5=0. 8; • Pc=0. 8 (0. 9+0. 9 -0. 81)(0. 8+0. 80. 64)+0. 1(0. 9 -0. 8+0. 9 0. 8 -0. 72 -0. 81)0. 8∙ 0. 1∙(0. 9+0. 9 -0. 81)(0. 8+0. 80. 64)(0. 72+0. 64∙ 0. 81)=0. 938.

Расчет надежности по графу работоспособности. (Марковские модели надежности) • Наиболее иллюстративным методом расчета надежности восстанавливаемых систем является метод, основанный на составлении графа переходов изделия в различные состояния работоспособности

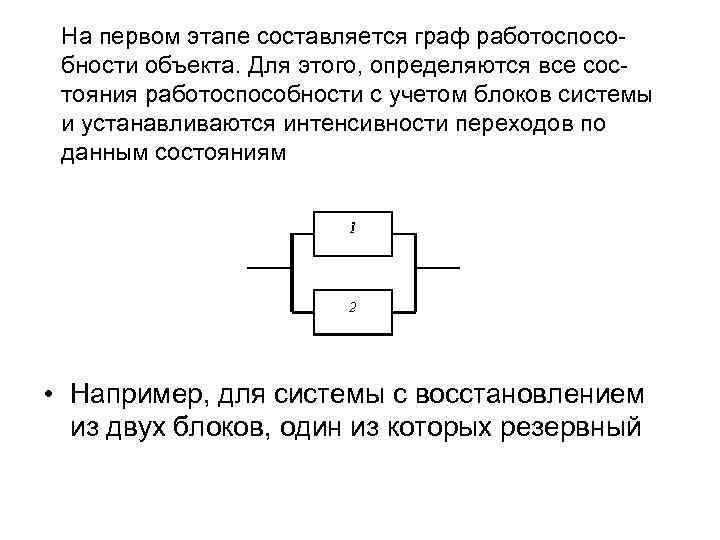
На первом этапе составляется граф работоспособности объекта. Для этого, определяются все состояния работоспособности с учетом блоков системы и устанавливаются интенсивности переходов по данным состояниям • Например, для системы с восстановлением из двух блоков, один из которых резервный

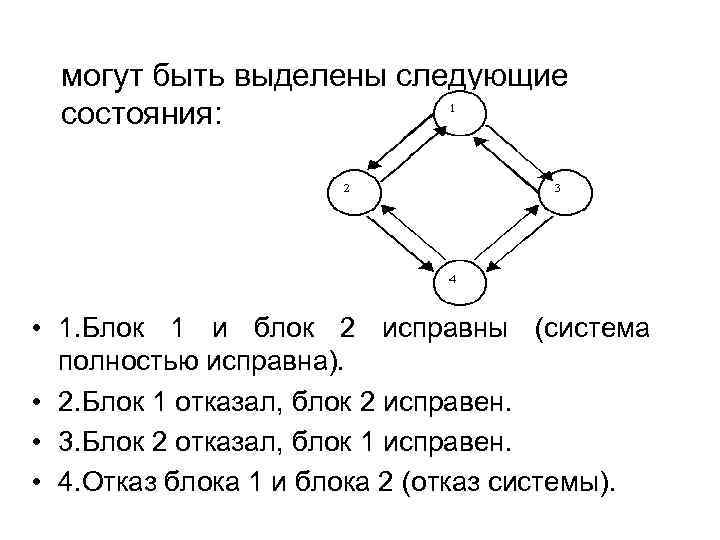
могут быть выделены следующие состояния: • 1. Блок 1 и блок 2 исправны (система полностью исправна). • 2. Блок 1 отказал, блок 2 исправен. • 3. Блок 2 отказал, блок 1 исправен. • 4. Отказ блока 1 и блока 2 (отказ системы).

Вероятности • вследствие предполагаемой ординарности потока равны нулю.

Система уравнений, определяющая вероятности состояний, имеет следующий вид: (1) • Уравнения системы, например первое, читается следующим образом:

вероятность того, что система во время t+Δt будет находиться в первом состоянии, равна произведению вероятности того, что система в момент времени t находилась в первом состоянии и вероятности отсутствия перехода во второе и третье состояния, или вероятности того, что система находилась во втором или третьем состоянии в момент t, умноженные на вероятности перехода из этих состояний в первое за промежуток Δt.

Если Δt достаточно мало, то • где ij-интенсивность перехода из i-го состояния в j-е состояние.

Система, записанная в функциях интенсивностей, имеет следующий вид (2), • Перенос Pi(t) везде влево и деление уравнений на t приводит к получению в левой части •

• При условии Δt —› 0,

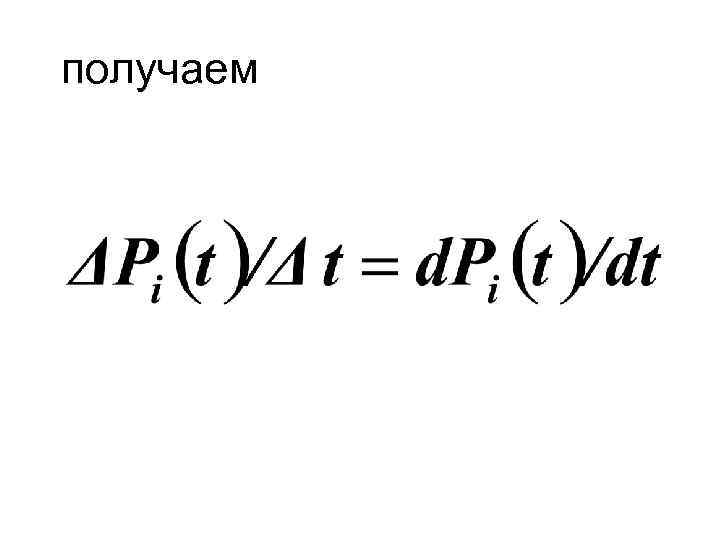
получаем

В окончательном виде система описывается следующими дифференциальными уравнениями (3) • При расчетах надежности систему уравнений составляют по графу работоспособности сразу в виде (3).

Очевидно, что в рассматриваемом примере коэффициент готовности равен вероятности застать систему в одном из трех работоспособных состояний: • Решение системы может быть выполнено известными способами.

Используем способ, основанный на преобразованиях Лапласа, переводящих систему дифференциальных уравнений в систему алгебраических уравнений: (4) • Из системы алгебраических уравнений находятся вероятности пребывания системы в состояниях Pi(z). • .

В случаях, когда вероятности состояний являются постоянными, что характерно для установившегося режима работы система уравнений (3) становится системой алгебраических уравнений, • Добавление последнего уравнения является обязательным и необходимым для закрытия системы.

Определение среднего времени наработки на отказ системы с восстановлением Время наработки на отказ определяется как

В то же время преобразование Лапласа определяется следующей формулой • то есть при z=0, T=P(z).

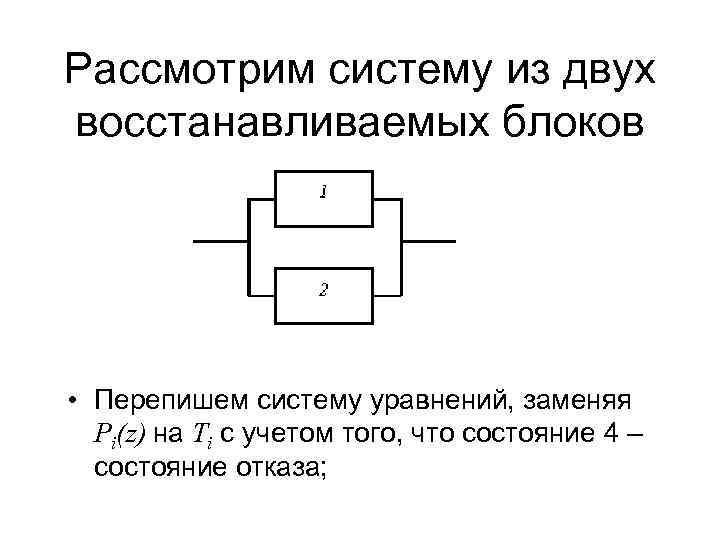
Рассмотрим систему из двух восстанавливаемых блоков • Перепишем систему уравнений, заменяя Pi(z) на Ti с учетом того, что состояние 4 – состояние отказа;

В результате P 4(z) = T 4 = 0, а также исчезает строка, соответствующая , d. P 4(t)/dt • Среднее время наработки на отказ всей системы T = T 1 + T 2 + T 3, так как 1, 2, 3 состояния работоспособности.