Рассмотрим преобразования линейного уравнения ax by

Рассмотрим преобразования линейного уравнения ax + by + с = 0; by = - ax – c ; y= b y=- a x- c b b. Введя обозначения - a = k, - c = m, получаем y = kx + m. b b. Таким образом, линейное уравнение (1) с двумя переменными x и y всегда можно преобразовать к виду y = kx + m, (2) где k, m – числа (коэффициенты), причем k 0. Этот частный вид линейного уравнения будем называть ЛИНЕЙНОЙ ФУНКЦИЕЙ. (1)

Линейная функция – это специальный вид линейного уравнения с двумя переменными. Графиком уравнения y = kx + m, как всякого линейного уравнения с двумя переменными, является прямая – ее называют также графиком линейной функции y = kx + m Т Графиком линейной функции y = kx + m является прямая

Пусть, например, y = 2 x + 3. Тогда : если x = 0, то y =3; если x = 1, то y =5; если x = -1, то y =1; если x = 3, то y =9 и т. д. х 0 1 -1 3 y 3 5 1 9 Значения у из второй строки таблицы называют значениями линейной функции у = 2 х + 3, соответственно, в точках : х = 0, х = 1, х = -1, х=3 x – НЕЗАВИСИМАЯ ПЕРЕМЕННАЯ(или аргумент), y – ЗАВИСИМАЯ ПЕРЕМЕННАЯ

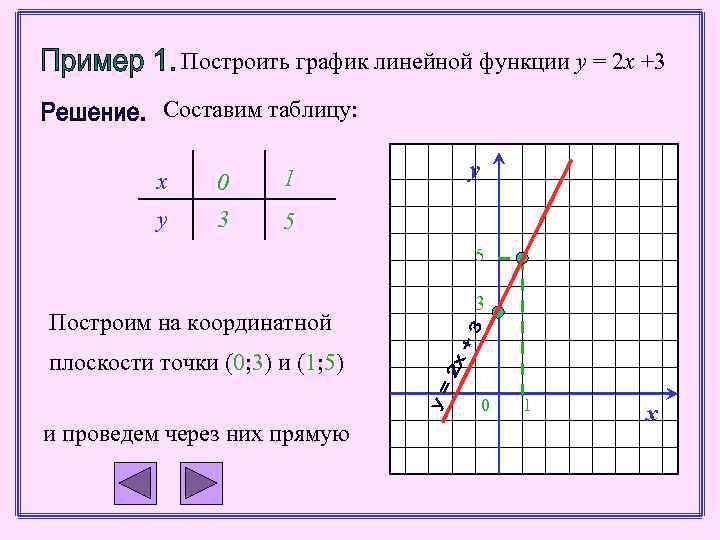
Построить график линейной функции у = 2 х +3 Составим таблицу: х 0 1 у 3 у 5 5 Построим на координатной 3 плоскости точки (0; 3) и (1; 5) 0 и проведем через них прямую 1 х

1 30 т 500 т угля Ежедневно привозили Сколько угля будет на складе через 2, 4, 10 дней? Пусть х – количество дней, то у – количество угля на складе (в тоннах) у= 30 х + 500 – линейная функция есть математическая модель ситуации Теперь нетрудно установить, что : если х = 2, то у = 560 если х = 4, то у = 620 если х = 10, то у = 800

А В 4 км/ч 2 15 км На каком расстоянии от А будет турист через 2 ч, 4 ч, 5 ч ходьбы? Математической моделью ситуации является линейная функция y =15 + 4 x, где х – время ходьбы (ч. ), у – расстояние от А (км). если х = 2, то у = 23 если х = 4, то у = 31 если х = 5, то у = 39

В задаче независимая переменная х может принимать только значения 1, 2, 3, …, поскольку х – число дней Следовательно , уточненная математическая модель первой ситуации : у = 30 х + 500, где х – натуральное число. В задаче независимая переменная х теоретически может принимать любое неотрицательное значение х=0, х=2, х=3, 5 … х Например, А что является геометрической моделью данного нестрогого двойного неравенства? х Отрезок [0 ; 6] 0 6 Значит уточненная модель выглядит так : у = 15 + 4 х, где х [0 ; 6] у = kx + m, х Х

Построить график линейной функции: y = -2 x + 1, х [-3 ; 2] Составим таблицу для линейной функции: y = -2 x +1 х -3 2 у 7 -3 у (-3; 7) и (2; -3) Найти наибольшее и наименьшее значения линейной функции на [-3 ; 2] 7 – наибольшее значение линейной функции y = -2 x + 1 унаиб = 7 -3 – наименьшее значение унаим = -3 7 -3 0 -3 1 2 х

х [-3 ; 2) х (- ; 1] у у 7 -3 0 -3 7 1 2 х -3 0 -3 1 2 х

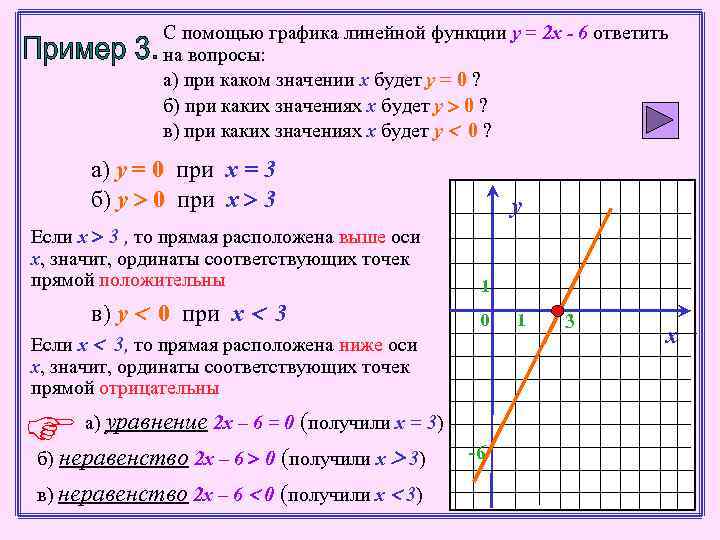
С помощью графика линейной функции у = 2 х - 6 ответить на вопросы: а) при каком значении х будет у = 0 ? б) при каких значениях х будет у 0 ? в) при каких значениях х будет у 0 ? а) у = 0 при х = 3 б) у 0 при х 3 Если х 3 , то прямая расположена выше оси х, значит, ординаты соответствующих точек прямой положительны в) у 0 при х 3 Если х 3, то прямая расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны у 1 0 а) уравнение 2 х – 6 = 0 (получили х = 3) б) неравенство 2 х – 6 0 (получили х 3) в) неравенство 2 х – 6 0 (получили х 3) -6 1 3 х

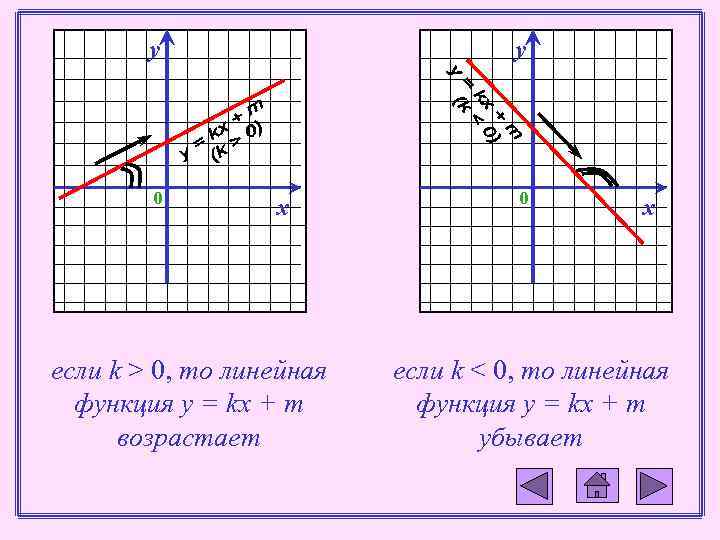
у 0 у х если k > 0, то линейная функция у = kx + m возрастает 0 х если k < 0, то линейная функция у = kx + m убывает

y = kx + m – это частный вид линейного уравнения с двумя переменными ax + by + с= 0, который называется л и н е й н о й ф у н к ц и е й Графиком линейной функции y = kx + m является п р я м а я Узнали, как найти наибольшее и наименьшее значения линейной функции y = kx + m Узнали в каких случаях линейная функция y = kx + m в о з р а с т а е т или у б ы в а е т