 Рассмотрим две формулы: ei = cos + i sin + cos = (ei + e-i )/2. e-i = cos + i sin – sin = (ei – e-i )/2 i. Дадим геометрическую интерпретацию операциям сложения, вычитания, умножения, деления комплексных чисел. Рассмотрим два комплексных числа z 1 и z 2. Эти комплексные числа на комплексной плоскости могут быть изображены векторами. Сумма z 1 + z 2 двух комплексных чисел может быть найдена путем сложения z 1 и z 2 как векторов по правилу параллелограмма. Разность z 1 – z 2 строится как сумма z 1 и –z 2. 1
Рассмотрим две формулы: ei = cos + i sin + cos = (ei + e-i )/2. e-i = cos + i sin – sin = (ei – e-i )/2 i. Дадим геометрическую интерпретацию операциям сложения, вычитания, умножения, деления комплексных чисел. Рассмотрим два комплексных числа z 1 и z 2. Эти комплексные числа на комплексной плоскости могут быть изображены векторами. Сумма z 1 + z 2 двух комплексных чисел может быть найдена путем сложения z 1 и z 2 как векторов по правилу параллелограмма. Разность z 1 – z 2 строится как сумма z 1 и –z 2. 1
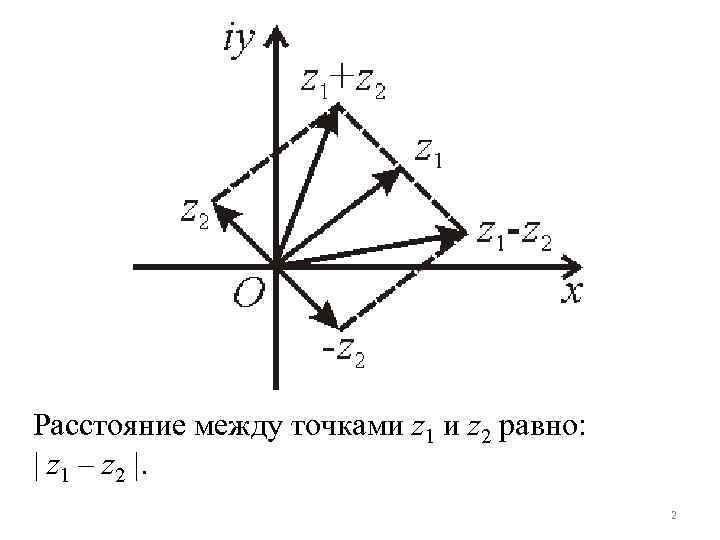 Расстояние между точками z 1 и z 2 равно: z 1 – z 2 . 2
Расстояние между точками z 1 и z 2 равно: z 1 – z 2 . 2
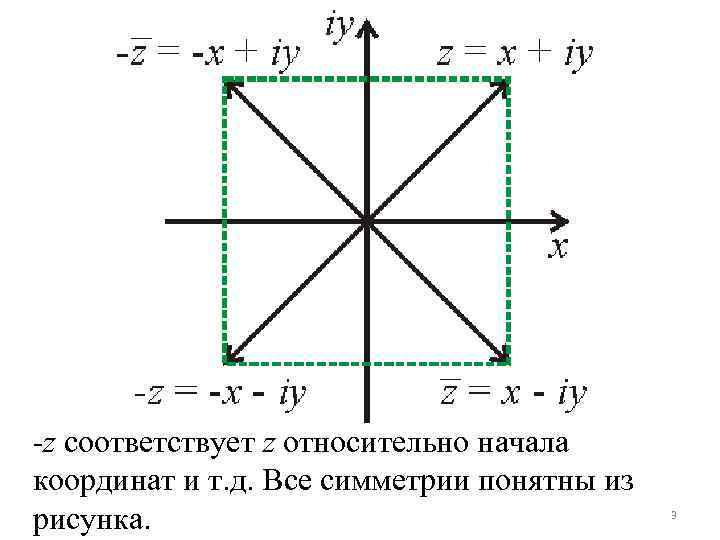 -z соответствует z относительно начала координат и т. д. Все симметрии понятны из рисунка. 3
-z соответствует z относительно начала координат и т. д. Все симметрии понятны из рисунка. 3
 Для умножения и деления комплексных чисел нужно воспользоваться показательной формой записи. z 1 = z 1 ei 1, z 2 = z 2 ei 2. 1. Произведение: z 1 z 2 = z 1 z 2 ei( 1 + 2). Доказательство. z 1 z 2 = z 1 z 2. ei 1 ei 2 = (cos 1 + isin 1)(cos 2 + isin 2) = (cos 1 cos 2 - sin 1 sin 2) + i(sin 1 cos 2 + cos 1 sin 2) = cos( 1 + 2) + isin( 1 + 2) = = ei( 1 + 2). Ч. т. д. 4
Для умножения и деления комплексных чисел нужно воспользоваться показательной формой записи. z 1 = z 1 ei 1, z 2 = z 2 ei 2. 1. Произведение: z 1 z 2 = z 1 z 2 ei( 1 + 2). Доказательство. z 1 z 2 = z 1 z 2. ei 1 ei 2 = (cos 1 + isin 1)(cos 2 + isin 2) = (cos 1 cos 2 - sin 1 sin 2) + i(sin 1 cos 2 + cos 1 sin 2) = cos( 1 + 2) + isin( 1 + 2) = = ei( 1 + 2). Ч. т. д. 4
 2. Частное: Доказательство. Самостоятельно. 3. Возведение в степень: zn = z n ein. n – натуральное. Из свойства 1 следует, что при умножении комплексных чисел, модули перемножаются, а аргументы складываются: z = z 1 z 2 , arg z = 1 + 2. 5
2. Частное: Доказательство. Самостоятельно. 3. Возведение в степень: zn = z n ein. n – натуральное. Из свойства 1 следует, что при умножении комплексных чисел, модули перемножаются, а аргументы складываются: z = z 1 z 2 , arg z = 1 + 2. 5
 При делении модули комплексных чисел делятся, а аргументы вычитаются: , arg z = 1 + 2. Свойство 3 нужно для того, чтобы получить формулу Муавра: (cos + isin )n = cosn + isinn Она связывает n-тую (cos + isin )n с cosn и sinn. 6
При делении модули комплексных чисел делятся, а аргументы вычитаются: , arg z = 1 + 2. Свойство 3 нужно для того, чтобы получить формулу Муавра: (cos + isin )n = cosn + isinn Она связывает n-тую (cos + isin )n с cosn и sinn. 6
 Геометрическая интерпретация множеств комплексных чисел. 1. Пусть множество комплексных чисел Z удовлетворяет условию: - действительное число. Это окружность. 7
Геометрическая интерпретация множеств комплексных чисел. 1. Пусть множество комплексных чисел Z удовлетворяет условию: - действительное число. Это окружность. 7
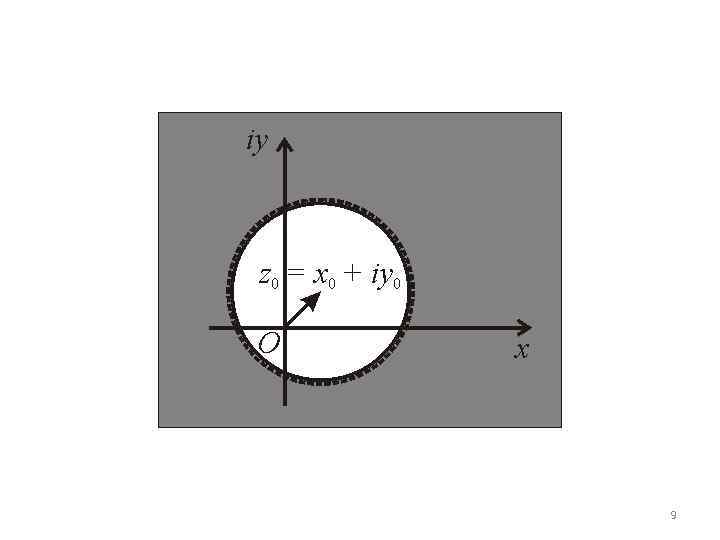
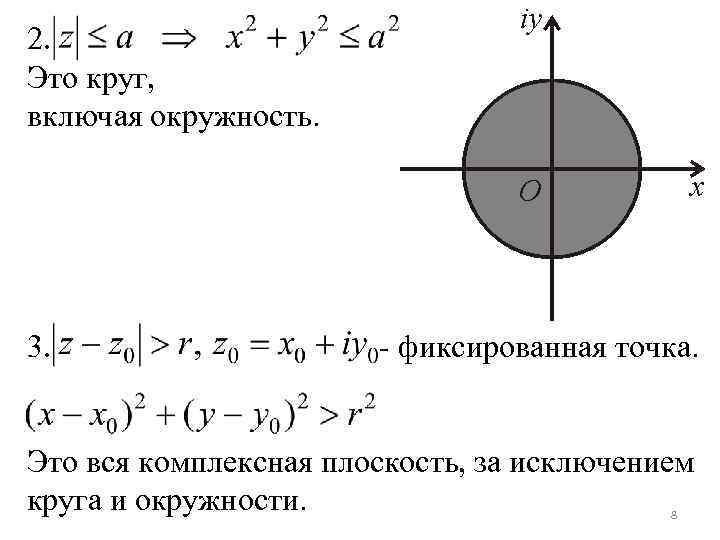 2. Это круг, включая окружность. 3. - фиксированная точка. Это вся комплексная плоскость, за исключением круга и окружности. 8
2. Это круг, включая окружность. 3. - фиксированная точка. Это вся комплексная плоскость, за исключением круга и окружности. 8
 9
9
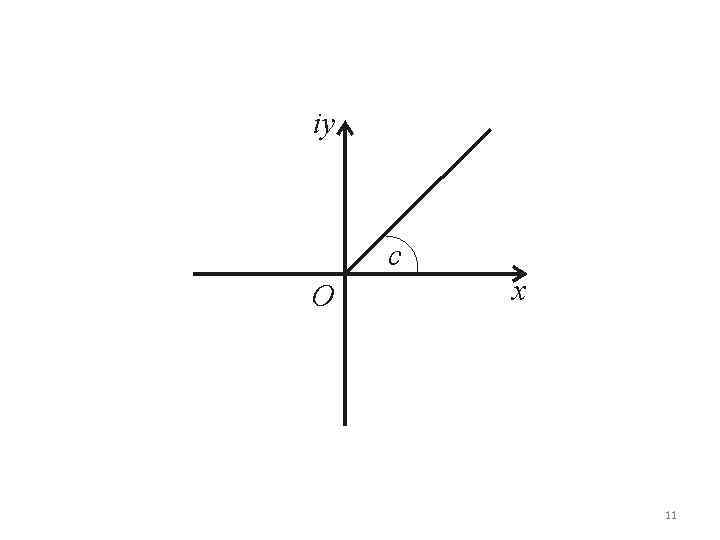
 4. Это кольцо. 5. Это множество точек представляет собой луч, выходящий из начала координат, расположенный под углом c к оси x. 10
4. Это кольцо. 5. Это множество точек представляет собой луч, выходящий из начала координат, расположенный под углом c к оси x. 10
 11
11
 § 8. 2. Извлечение корня из комплексного числа. Пусть дано комплексное число Корнем n-той степени из комплексного числа w , обозначаемый называется комплексное число z такое, что. Рассмотрим уравнение. Пусть w – комплексное число Тогда Два комплексных числа равны тогда и только тогда, когда: 12
§ 8. 2. Извлечение корня из комплексного числа. Пусть дано комплексное число Корнем n-той степени из комплексного числа w , обозначаемый называется комплексное число z такое, что. Рассмотрим уравнение. Пусть w – комплексное число Тогда Два комплексных числа равны тогда и только тогда, когда: 12
 Добавляем к , так как аргумент однозначно не определяется. Покажем, что среди полученного бесконечного множества существует только n различных чисел, которые принимаются за значение корня n-той степени из комплексного числа. 13
Добавляем к , так как аргумент однозначно не определяется. Покажем, что среди полученного бесконечного множества существует только n различных чисел, которые принимаются за значение корня n-той степени из комплексного числа. 13
 Модули всех комплексных чисел одинаковы и равны. Отличаться они будут только своими аргументами. имеет аргумент 14
Модули всех комплексных чисел одинаковы и равны. Отличаться они будут только своими аргументами. имеет аргумент 14
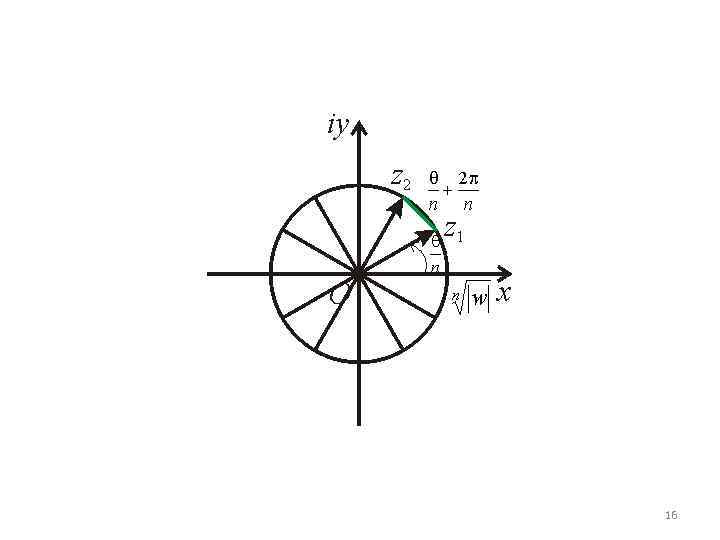
 Таким образом, если дано комплексное число w, то корней n-той степени из комплексного числа w, n и вычисляться они будут по следующей формуле Все значения находятся в вершинах вписанного в окружность n – угольника и могут быть интерпретированы следующим образом: 15
Таким образом, если дано комплексное число w, то корней n-той степени из комплексного числа w, n и вычисляться они будут по следующей формуле Все значения находятся в вершинах вписанного в окружность n – угольника и могут быть интерпретированы следующим образом: 15
 16
16