Рассеяние молекулярного пучка в газе Число молекул прошедших

Рассеяние молекулярного пучка в газе. Число молекул, прошедших расстояние х без столкновений. Число молекул, свободный пробег которых заключен в пределах от х до х + dx: Вязкость газа (внутреннее трение). Закон Ньютона. Закон Стокса. Коэффициент вязкости газа.

Теплопроводность газа. Коэффициент теплопроводности газа. Закон Фурье. Закон диффузии Фика Коэффициент диффузии газа

Термическая диффузия. Если в объеме V находится смесь газов и в нем создать градиент температуры, то равномерное распределение газа по объему нарушается: обычно в более теплых областях объема увеличивается концентрация легкой компоненты смеси, а в более холодных - тяжелой. Это явление носит название термической диффузии. При стационарном распределении температур возникает градиент концентраций. Он создает обычную диффузию, а стационарность процесса обмена молекулами обеспечивается термической диффузией. Эти 2 процесса идут в разные стороны Явление термодиффузии нельзя объяснить простыми молекулярнокинетическими представлениями. Было выяснено, что в этом явлении существенную роль играют силы отталкивания между молекулами компонентов при их столкновении, которые приближенно можно считать убывающими по закону 1/гn, где г — расстояние между молекулами. Используя явление термодиффузии был разделен целый ряд изотопов.

Диффузия в твердых телах. В твердых телах рассматривают три основных механизма диффузии (и самодиффузии): 1. Соседние атомы в решетке обмениваются местами в решетке. Обмен этот может, например, явиться следствием поворота участвующей в ней пары атомов вокруг сред- средней точки. 2. Атом, находящийся на «своем» месте в узле решетки, покидает его и располагается в междоузлии, а затем мигрирует по междоузельным позициям. 3. Атомы из узлов решетки переходят в незанятые узлы, так называемые вакансии. Этот переход атомов на вакантные места эквивалентен перемещению самих вакансий в направлении, обратном направлению движения атомов.

Соотношение Нернста-Эйнштейна. Рассмотрим диффузию ионов при наличии электрического поля. На заряженный ион действует постоянная сила F, пропорциональная напряженности электрического поля. При отсутствии внешней силы F движение иона было бы полностью беспорядочным. При наличии постоянной силы F появляется преимущественное направление скорости иона u. Если электрическое поле не очень сильное, то установившаяся скорость иона u пропорциональна приложенной к нему силе F. В этом случае можно ввести понятие подвижность частицы μ, которое является коэффициентом пропорциональности между регулярной скоростью и и силой F: Несущественно, что частицами являются ионы. Все сказанное справедливо и для молекул, и для любых других частиц. Если F — сила, действующая на частицу «газа» в силовом поле, то потенциальная энергия ее в этом поле будет = — Fх (где х- координата частицы).

Если состояние стационарно, то концентрация частиц «газа» меняется в пространстве в соответствии с формулой Больцмана Поскольку есть градиент концентрации, в газе происходит диффузия. Диффузионный поток в положительном направлении оси X определяется выражением А так как «газ» находится в силовом поле, то существует также и «силовой поток» молекул с плотностью В состоянии равновесия (так называемое «динамическое равновесие» ) должно быть Подставляя сюда предыдущие выражения, получаем соотношение Нернста. Эйнштейна:

Броуновское движение Броуновским движением называется беспорядочное движение малых частиц (размерами в несколько мкм и менее), взвешенных в жидкости или газе, происходящее под действием не скомпенсированных ударов молекул окружающей среды. Случайное блуждание. Рассмотрим положение броуновской частицы через некоторые фиксированные промежутки времени t. По истечении n наблюдений (или за время t= n t) частица сместится из нулевого положения в точку с радиус- вектором rn. где — средний квадрат смещения частицы на i-м шаге в серии опытов; второй сумме является средней величиной скалярного произведения при i-м шаге на перемещение при j-м шаге в различных опытах.

Среднее значение скалярного произведения неодинаковых векторов смещения обращается в ноль из-за равноправия всех направлений смещения. Таким образом, средний квадрат смещения частицы за время t где a 2 = Таким образом, величина среднего квадрата смещения броуновской частицы пропорциональна времени наблюдения t. Для того чтобы определить коэффициент пропорциональности α, рассмотрим силы, действующие на частицу. Video.

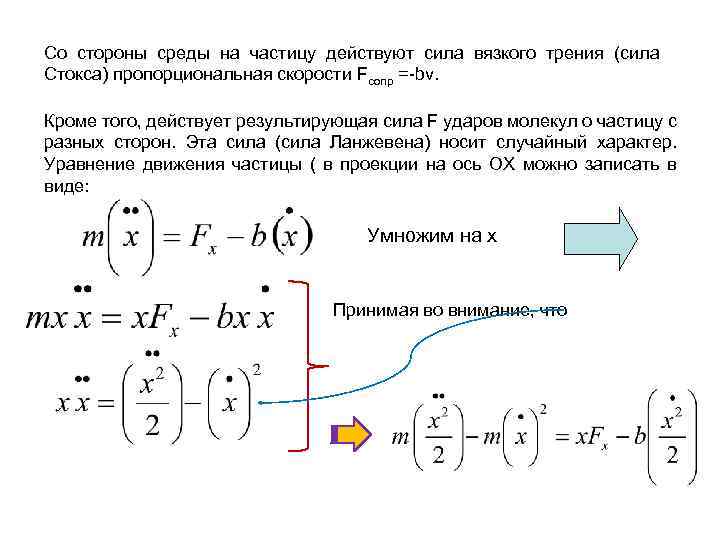Со стороны среды на частицу действуют сила вязкого трения (сила Стокса) пропорциональная скорости Fсопр =-bv. Кроме того, действует результирующая сила F ударов молекул о частицу с разных сторон. Эта сила (сила Ланжевена) носит случайный характер. Уравнение движения частицы ( в проекции на ось ОХ можно записать в виде: Умножим на х Принимая во внимание, что

Усредним полученное уравнение по всем наблюдениям, учитывая, что среднее значение производной равно производной среднего значения. Тогда Координата x частицы и соответствующая проекция силы Ланжевене Fx являются случайными и не зависящими друг от друга величинами. Поэтому С другой стороны

Тогда уравнение на средние характеристики движения примет вид Решение данного уравнения можно записать в виде Для больших интервалов времени наблюдения t вторым слагаемым можно пренебречь. Тогда

Величина D=k. T/b характеризует количество частиц данного вида, проходящих через единичную площадку в единицу времени и называется коэффициентом диффузии. Коэффициент диффузии зависит от температуры и свойств жидкости, а также от размеров и формы движущихся частиц. Тогда дифференциальное уравнение на средний квадрат X-смещения броуновской частицы примет вид формула Эйнштейна. Смолуховского. При движении в плоскости XOY среднее значение квадрата отклонения частицы, выражается через средние квадраты X- и Y-координат Согласно формуле Стокса для частицы шарообразной формы

Вращательное броуновское движение Рассмотрим зеркальце, подвешенное вертикально на упругой нити. Вследствие взаимодействия с молекулами воздуха зеркало будет испытывать крутильные колебания вокруг оси. Поэтому освещая поверхность зеркала лучом света, можно легко зафиксировать смещение луча света даже при весьма малых поворотах зеркала. Уравнение крутильных колебаний имеет вид где модуль кручения нити, а знак минус учитывает, что момент сил упругости нити стремится вернуть зеркало в положение равновесия. Малые крутильные колебания являются гармоническими, поэтому при T= 290 К, =10 -15 Н-м получаем < 2> ~ 4 х10 -6, что хорошо измеряется и позволяет определить постоянную Больцмана k.

Коэффициенты переноса и их зависимость от давления Сопоставим полученные в предыдущих параграфах выражения для законов: диффузии - перенос массы (закон Фика) внутреннего трение-перенос импульса (закон Ньютона) теплопроводности – перенос энергии (закон Фурье)

Выражения для соответствующих коэффициентов: диффузии внутреннего трения теплопроводности Учитывая, что nm= легко установить следующие взаимосвязи: Проанализируем эти соотношения, как функции давления.

Средняя скорость молекул с пропорциональна Т 1/2 и не зависит от давления, то D ~ λ, поэтому при обычных давлениях в области вакуума, где λ определяется размерами сосуда При постоянной температуре плотность газа пропорциональна его давлению р. при обычных давлениях в области вакуума Поскольку удельная теплоемкость газа cv — величина постоянная, то теплопроводность газа будет себя вести так же, как и вязкость: при обычных давлениях в области вакуума