 Распространение тепла в неограниченном стержне 1
Распространение тепла в неограниченном стержне 1
 Использует метод Фурье 2
Использует метод Фурье 2
 3
3
 4
4
 5
5
 6
6
 7
7
 8
8
 9
9
 Эта формула, называемая интегралом Пуассона, представляет собой решение поставленной задачи о распространении тепла в неограниченном стержне. 10
Эта формула, называемая интегралом Пуассона, представляет собой решение поставленной задачи о распространении тепла в неограниченном стержне. 10
 Случай стержня, ограниченного с одной стороны 11
Случай стержня, ограниченного с одной стороны 11
 12
12
 Уравнение теплопроводности с неоднородными граничными условиями 13
Уравнение теплопроводности с неоднородными граничными условиями 13
 Произведем замену переменных T = V + x 14
Произведем замену переменных T = V + x 14
 15
15
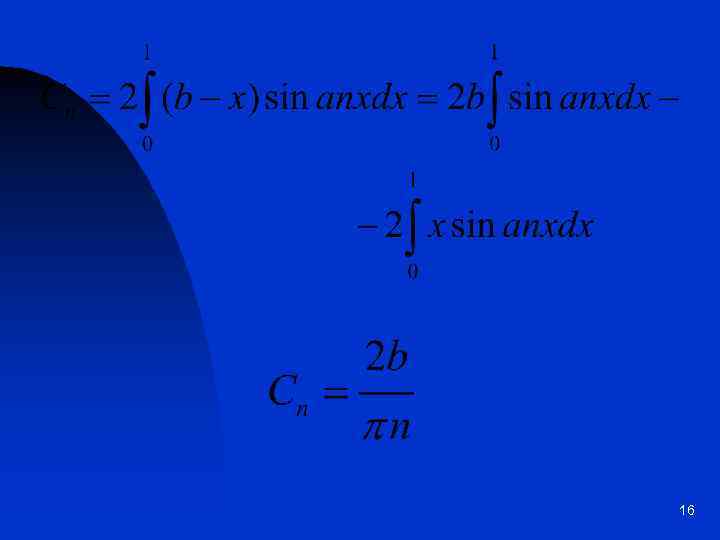 16
16
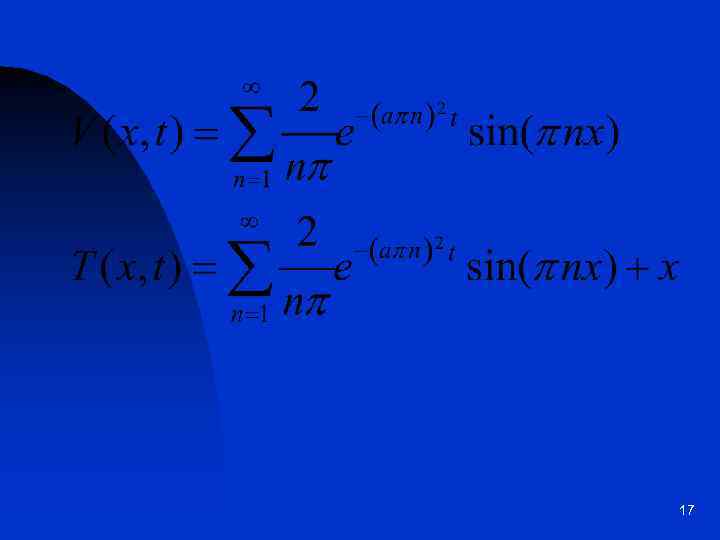 17
17
 Уравнение теплопроводности стержня, излучающего с боковой поверхности 18
Уравнение теплопроводности стержня, излучающего с боковой поверхности 18
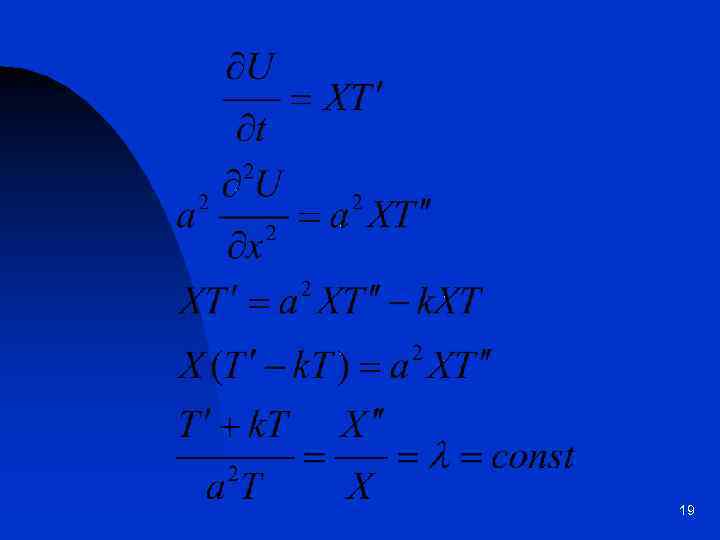 19
19
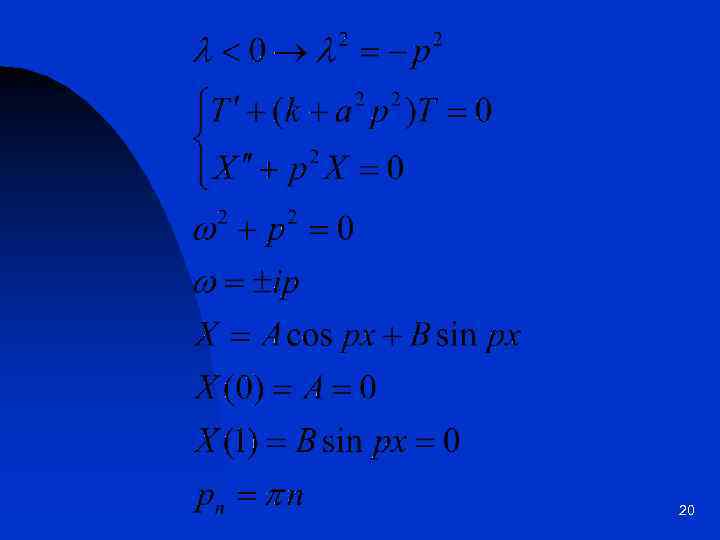 20
20
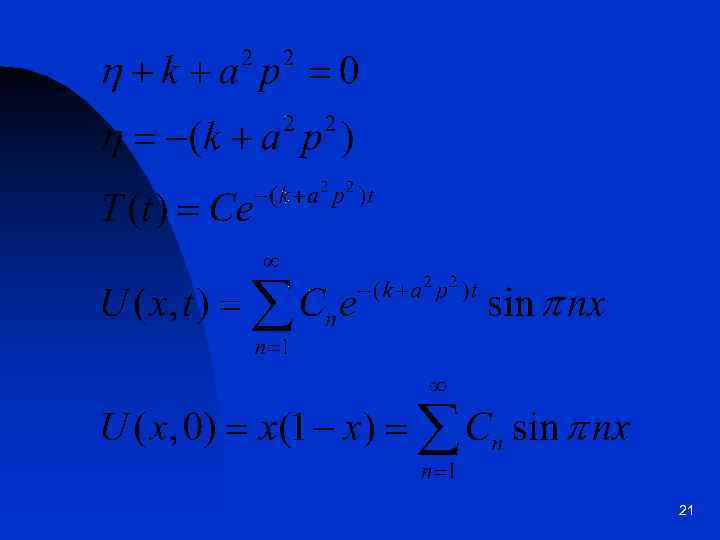 21
21
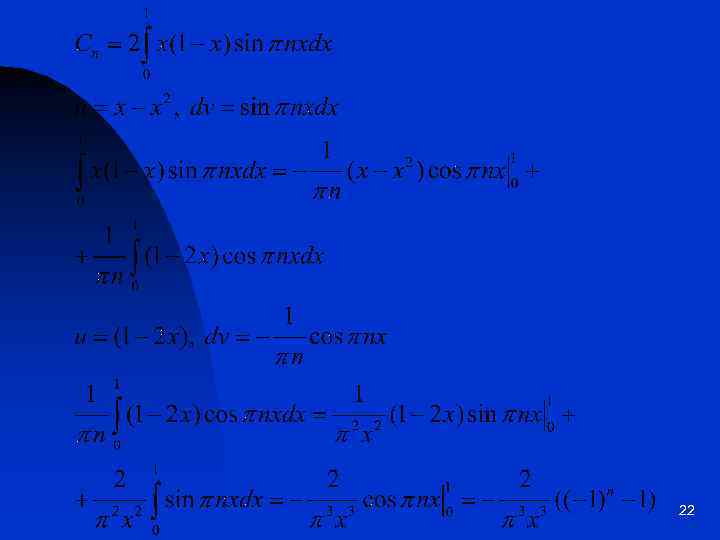 22
22
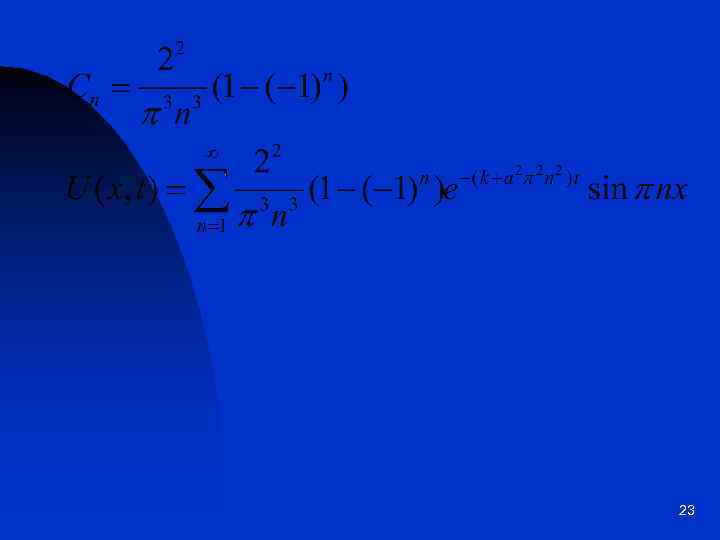 23
23
 Определение критической массы урана 24
Определение критической массы урана 24
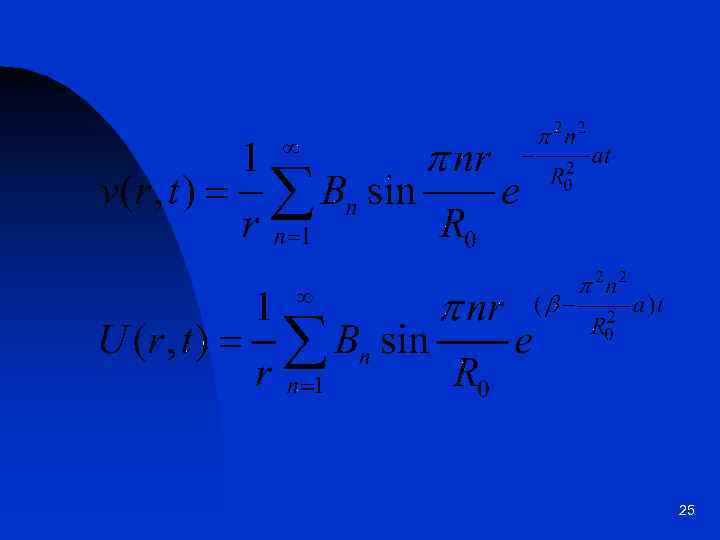 25
25
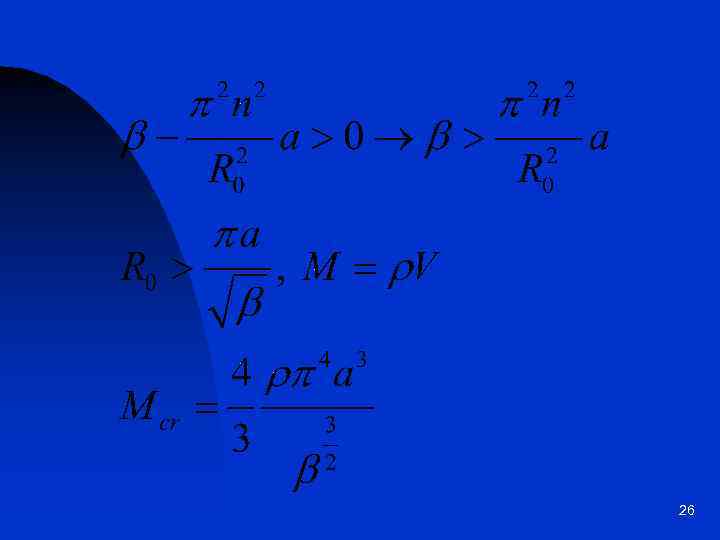 26
26
 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА – ур-ие Лапласа – ур-ие Пуассона 27
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА – ур-ие Лапласа – ур-ие Пуассона 27
 1. Задача Дирихле В области D(x, y, z) найти непрерывную, дважды дифференцируемую функцию, удовлетворяющую уравнению эллиптического типа и следующему граничному условию: – на границе области известны значения искомой функции. 28
1. Задача Дирихле В области D(x, y, z) найти непрерывную, дважды дифференцируемую функцию, удовлетворяющую уравнению эллиптического типа и следующему граничному условию: – на границе области известны значения искомой функции. 28
 2. Задача Неймана Найти решение уравнения, удовлетворяющее следующему граничному условию: – на границе области известна производная искомой функции по нормали. n – внешняя нормаль к границе G в точке (x, у). 29
2. Задача Неймана Найти решение уравнения, удовлетворяющее следующему граничному условию: – на границе области известна производная искомой функции по нормали. n – внешняя нормаль к границе G в точке (x, у). 29
 3. Смешанная задача Найти решение уравнения, удовлетворяющее условию: где n – внешняя нормаль к границе области D. 30
3. Смешанная задача Найти решение уравнения, удовлетворяющее условию: где n – внешняя нормаль к границе области D. 30
 Стационарное (установившееся ) распределение температуры в однородном теле Пусть имеется однородное тело, ограниченное поверхностью G. Температура в различных точках тела удовлетворяет уравнению: Если процесс установившийся, т. е. если температура не зависит от времени, а зависит только от координат точек тела, то Ut’ = 0 и, следовательно, температура удовлетворяет уравнению Лапласа: 31
Стационарное (установившееся ) распределение температуры в однородном теле Пусть имеется однородное тело, ограниченное поверхностью G. Температура в различных точках тела удовлетворяет уравнению: Если процесс установившийся, т. е. если температура не зависит от времени, а зависит только от координат точек тела, то Ut’ = 0 и, следовательно, температура удовлетворяет уравнению Лапласа: 31
 Чтобы температура в теле определялась однозначно из этого уравнения, нужно знать, например, температуру на поверхности G: Эта задача называется задачей Дирихле или первой краевой задачей. 32
Чтобы температура в теле определялась однозначно из этого уравнения, нужно знать, например, температуру на поверхности G: Эта задача называется задачей Дирихле или первой краевой задачей. 32
 Если на поверхности тела температура неизвестна, а известен тепловой поток в каждой точке поверхности, который пропорционален , то на поверхности G будем иметь граничное условие: Задача нахождения решения уравнения, удовлетворяющего краевому данному условию, называется задачей Неймана или второй краевой задачей. 33
Если на поверхности тела температура неизвестна, а известен тепловой поток в каждой точке поверхности, который пропорционален , то на поверхности G будем иметь граничное условие: Задача нахождения решения уравнения, удовлетворяющего краевому данному условию, называется задачей Неймана или второй краевой задачей. 33
 Задача Дирихле для уравнения Лапласа в круге 34
Задача Дирихле для уравнения Лапласа в круге 34
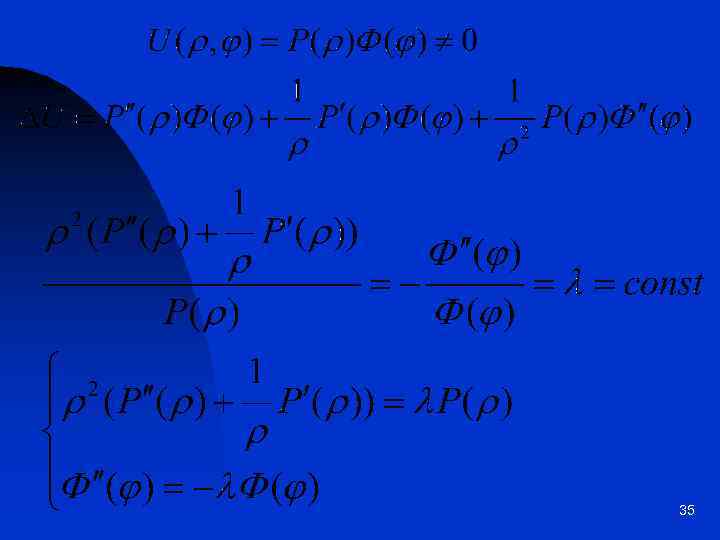 35
35
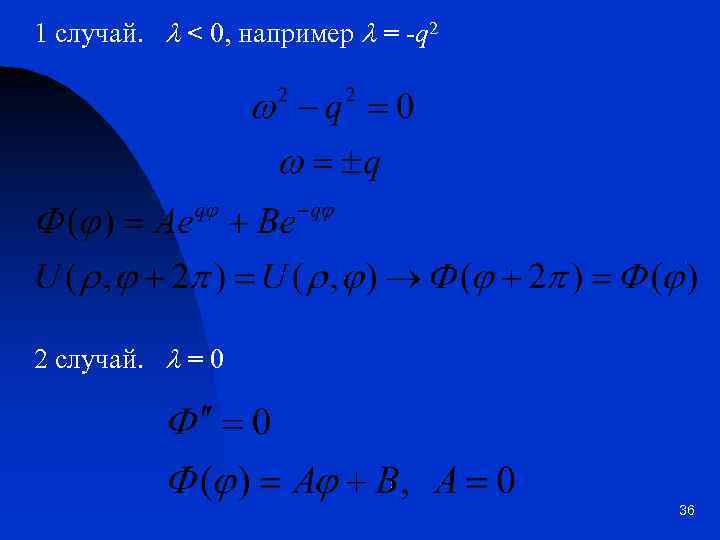 1 случай. l < 0, например l = -q 2 2 случай. l = 0 36
1 случай. l < 0, например l = -q 2 2 случай. l = 0 36
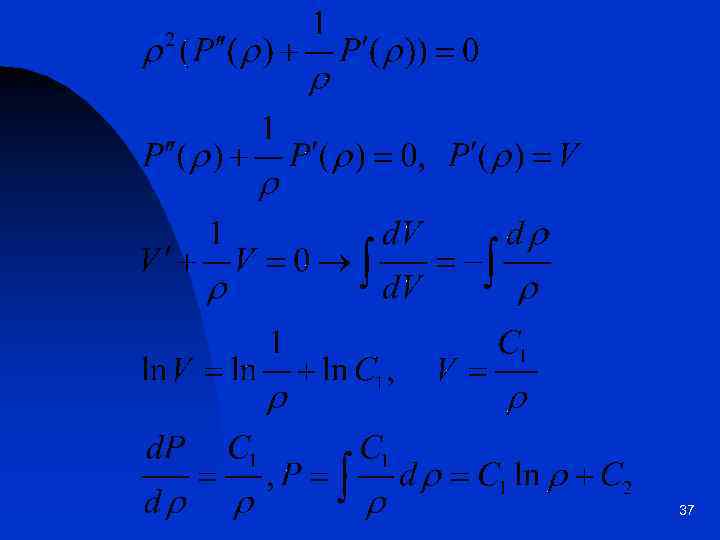 37
37
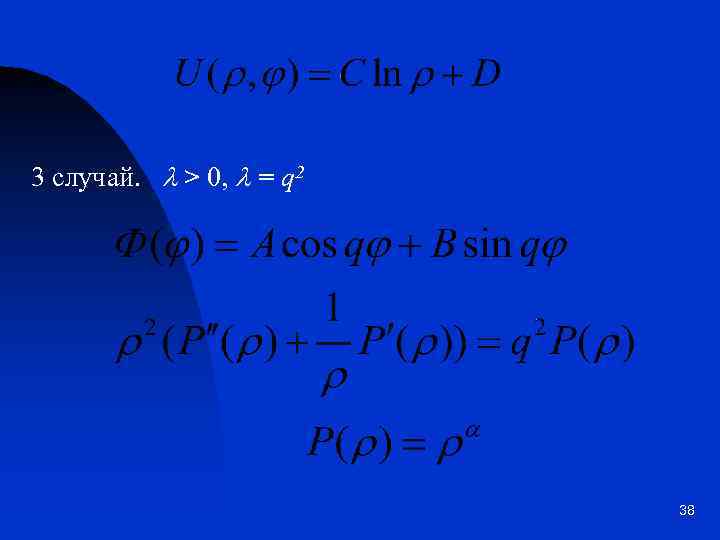 3 случай. l > 0, l = q 2 38
3 случай. l > 0, l = q 2 38
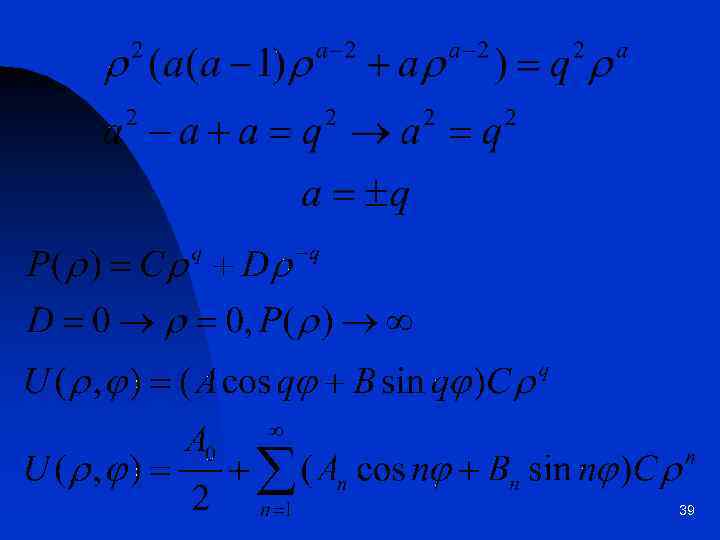 39
39
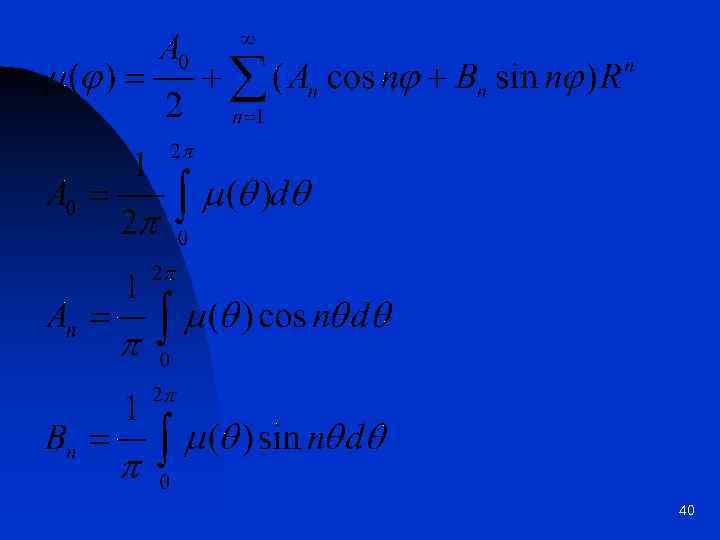 40
40
 – Формулы Эйлера 41
– Формулы Эйлера 41
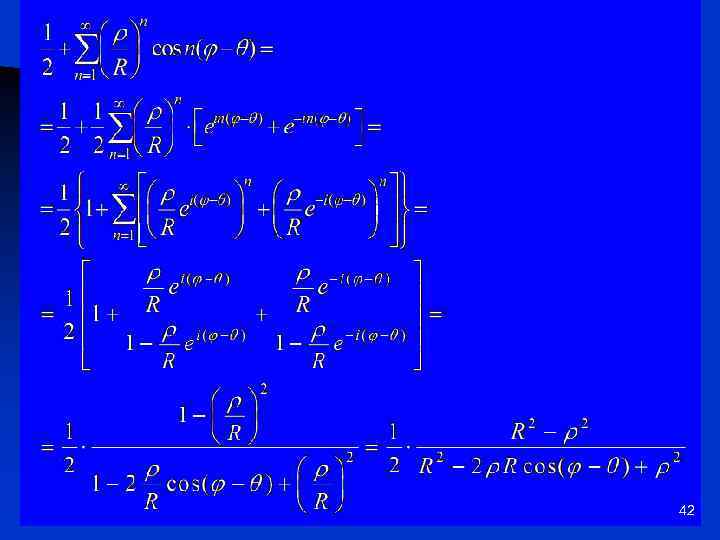 42
42
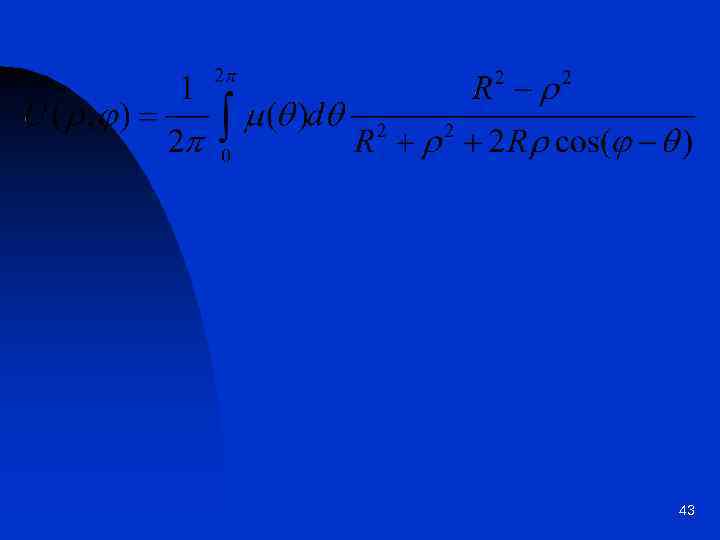 43
43
 Задача Дирихле для уравнения Лапласа в кольце 44
Задача Дирихле для уравнения Лапласа в кольце 44
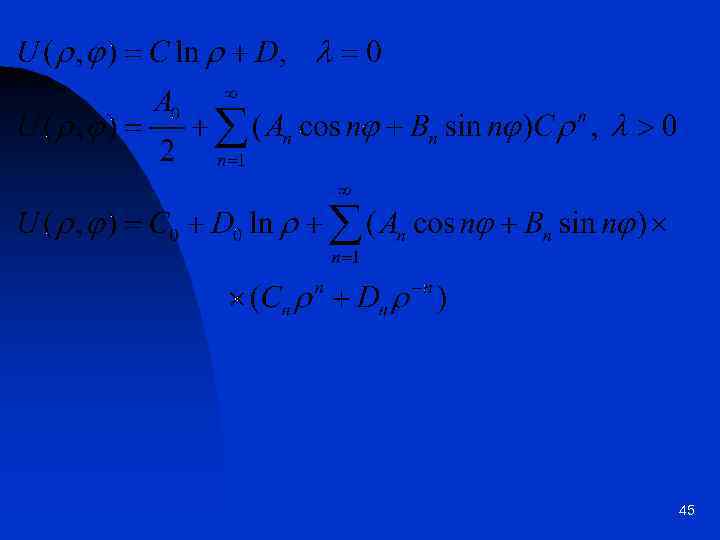 45
45
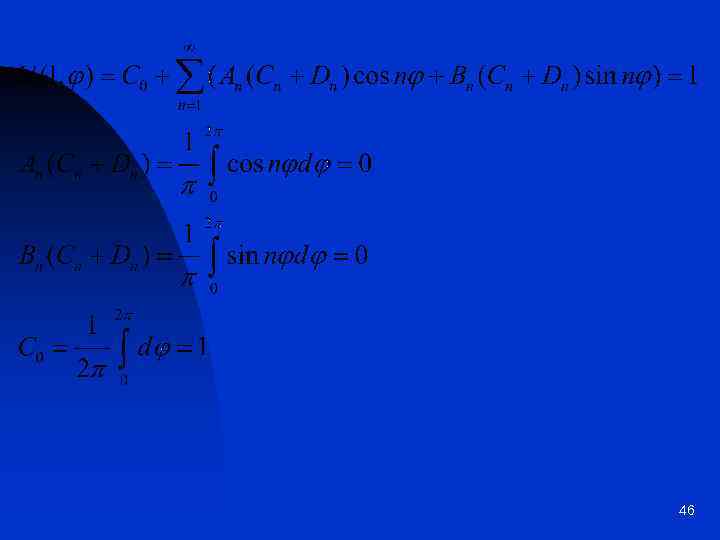 46
46
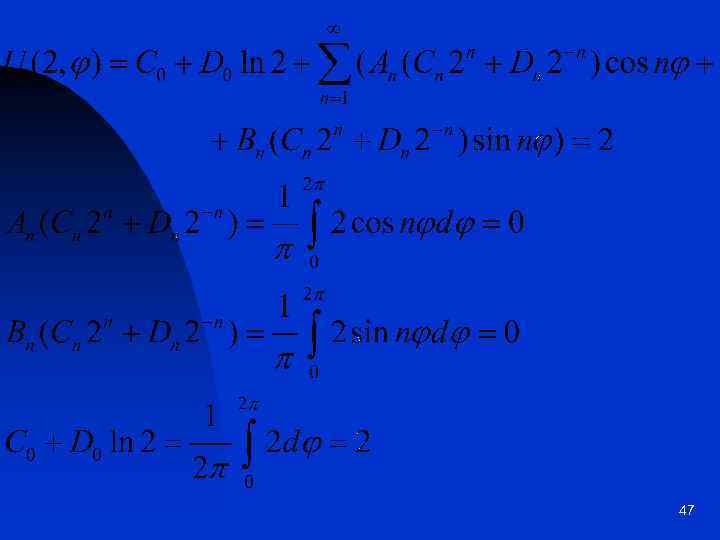 47
47
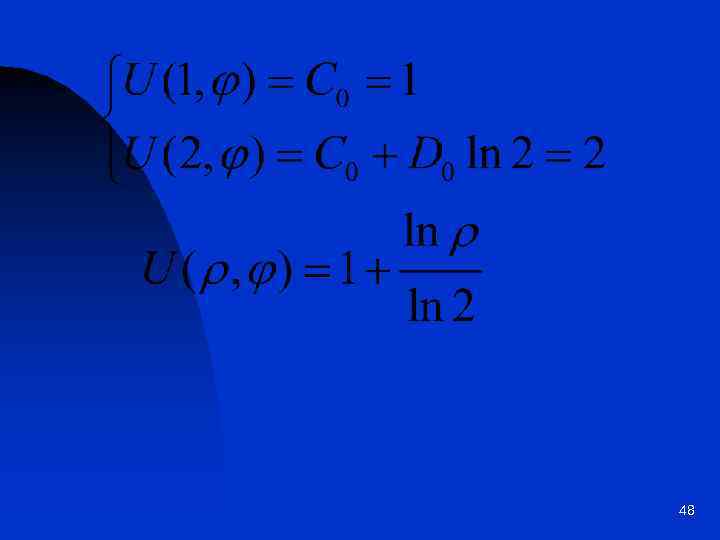 48
48