Распознавание образов.ppt
- Количество слайдов: 54

Распознавание образов Семинар по “Image processing and Pattern Recognition” Гостев И. М. Москва НИУ ВШЭ 2011 Gostev I. M. Shape Analysis

Основные задачи теории распознавания образов 1. Математическое описание образов. Наиболее удобным математическим описанием считается векторное описание образов. В этом случае каждому образу x ставится в соответствие некоторый вектор x= (x 1, x 2, …xn) признаков этого образа – элемент векторного пространства. Такое векторное пространство называется пространством признаков. Как правило, это пространство является конечномерным и метрическим. 2. Выбор наиболее информативных признаков, описывающих данный образ. Это одна из основных и важных задач в теории распознавания образов – найти минимальное количество признаков, наиболее информативно описывающих образы в данной системе (или задаче) распознавания. Полный набор выбранных для распознавания признаков называют алфавитом признаков. Минимальный же набор признаков, достаточный для решения данного класса задач распознавания, называют словарем признаков. 3. Описание классов распознаваемых образов. Эта задача сводится к определению границ классов. Границы классов могут быть заданы явно на этапе разработки системы распознавания или система сама должна их найти в процессе своей работы. 4. Нахождение оптимальных решающих процедур (методов классификации), т. е. методов соотнесение вектора признаков образа некоторому классу. 5. Оценка достоверности классификации образов. Эта оценка необходима, чтобы лицо, принимающее решение (это может быть и техническая система), связанное с отнесением образа тому или иному классу, могло оценить величину потерь, связанных с неправильной классификацией. Gostev I. M. Shape Analysis 2

Типы характеристик образов Выделяют следующие типы характеристик-признаков: 1. Физические характеристики, например, показания, снятые с различных датчиков. Физические характеристики могут быть детерминированными и вероятностными. Лучше всего физические характеристики описывать с помощью векторов и обрабатывать как элементы векторного пространства. 2. Качественные характеристики. Примерами качественных характеристик являются понятия «темный» , «светлый» , «высокий» и т. д. Такие характеристики могут быть описаны с помощью так называемых лингвистических переменных методами теории нечетких множеств. 3. Структурные характеристики. Эти характеристики употребительны для описания изображений сложных объектов или сцен. При описании структурных характеристик используется некоторый формальный язык (например, теория графов) 4. Логические характеристики – это высказывания, о которых имеет смысл говорить истины они или ложны. Признаком называют некоторое свойство измеренное на каждом объекте Gostev I. M. Shape Analysis 3

Типы систем распознавания Можно выделить несколько критериев классификации систем распознавания. Один из таких критериев – по характеру информации о признаках: детерминистские; вероятностные; логические; структурные; комбинированные. Другой критерий – по количеству априорной информации о распознаваемых объектах. Различают три основных типа систем распознавания. 1. Системы без обучения. Количество априорной информации достаточно для определения набора признаков и определения границ классов. 2. Системы, основанные на обучении с учителем. Количества априорной информации достаточно только для выбора алфавита признаков и формирования словаря признаков, но не для определения границ между классами. Системе распознавания предъявляется некоторое множество объектов, которое называется обучающим множеством (выборкой), с указанием к каким классам эти объекты принадлежат. Система сама должна настроить параметры правил классификации таким образом, чтобы выполнялось условие минимальности ошибки неправильной классификации. 3. Системы, основанные на самообучении (на объяснении). Количества априорной информации недостаточно даже для формирования словаря признаков. В этом случае в систему распознавания образов вводится список правил, объясняющий задачи распознавания образов. Этот список правил вырабатывается, как правило, экспертами - специалистами в данной области знаний, такие системы называют экспертными (интеллектуальными). Система распознавания, исходя из этого набора правил, должна сама сформировать словарь признаков и определить границы классов. При этом, как правило, используются логико-лингвистические методы обработки данных. Gostev I. M. Shape Analysis 4

Понятие решающих функций Одной из основных задач распознавания образов является задача описания классов. Предположим, что имеется некоторое (конечное) множество классов Ω = {ω1, . . . , ω m}. Каждый образ описывается некоторым набором признаков в пространстве признаков – вектором x. Все пространство признаков X разбивается на m + 1 попарно несовместных множеств (полную группу множеств) X 0, X 1, …, X m , Xi ∩ X i =∅ для всех i ≠ j , mi=0 Xi=X таким образом, что x є ωi, если x є X 0. Если же x є X 0 , то будем считать, что образ x попал в область неопределенности и в этом случае его классифицировать не будем. Таким образом, границами классов распознаваемых образов будем считать границы областей X i i = ( 0, 1, . . . , m). Автоматическое нахождение границ классов – одна из основных задач теории распознавания образов. Границы классов распознаваемых объектов можно определять по-разному, например, с помощью понятия решающей функции. Gostev I. M. Shape Analysis 5

Линейные решающие функции (ЛРФ) Gostev I. M. Shape Analysis 6
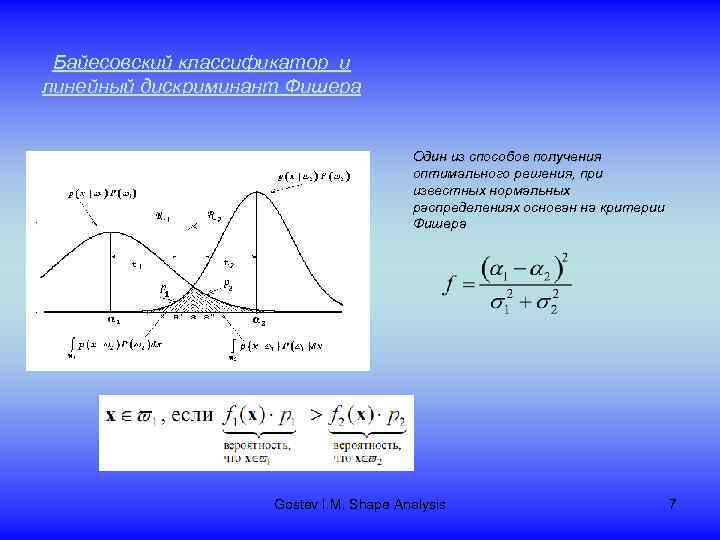
Байесовский классификатор и линейный дискриминант Фишера Один из способов получения оптимального решения, при известных нормальных распределениях основан на критерии Фишера Gostev I. M. Shape Analysis 7

Понятие метрики Gostev I. M. Shape Analysis 8
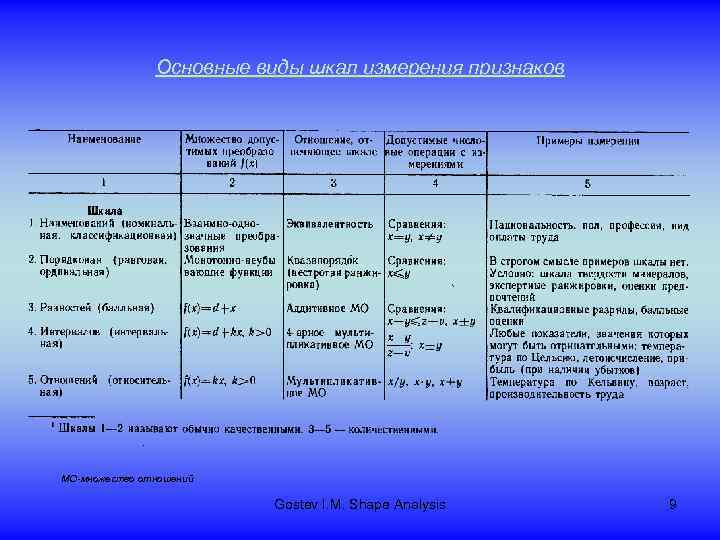
Основные виды шкал измерения признаков МО-множество отношений Gostev I. M. Shape Analysis 9

Классификация с помощью функций расстояния Gostev I. M. Shape Analysis 10

Способы измерения расстояний Чаще всего используют следующие метрики: Gostev I. M. Shape Analysis 11

Метрики Gostev I. M. Shape Analysis 12

Особенности метрик Gostev I. M. Shape Analysis 13
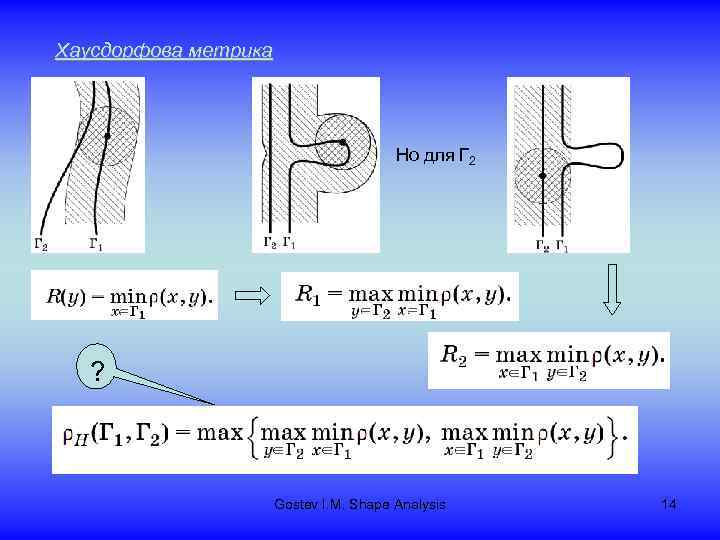
Хаусдорфова метрика Но для Г 2 ? Gostev I. M. Shape Analysis 14

Способы определения расстояния между объектом и классом Первый способ - определение расстояния до центра класса. Этот способ применяется в том случае, когда класс «хорошо описывается» одним эталонным образом – центром класса (качество такого описания может быть измерено величиной дисперсии элементов класса), а цена ошибки неправильной классификации не очень велика. В этом случае процедура определения расстояния состоит из следующих шагов. Gostev I. M. Shape Analysis 15

Определения расстояния между объектом и классом (2) X + Xs ? Gostev I. M. Shape Analysis 16

Определения расстояния между объектом и классом (3) Gostev I. M. Shape Analysis 17
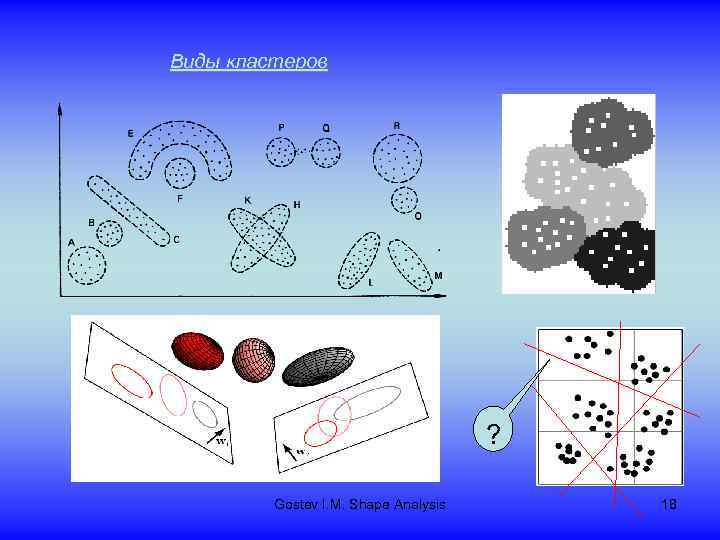
Виды кластеров ? Gostev I. M. Shape Analysis 18

Расстояния между классами (кластерами) Gostev I. M. Shape Analysis 19
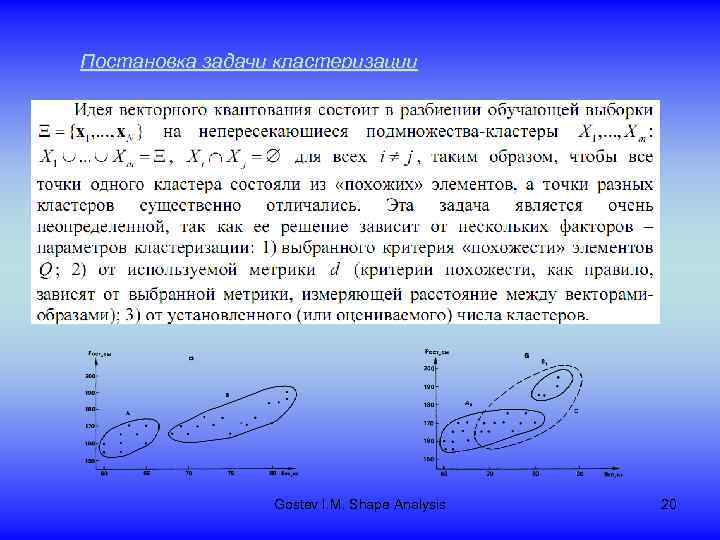
Постановка задачи кластеризации Gostev I. M. Shape Analysis 20

Критерии кластеризации Gostev I. M. Shape Analysis 21

Цели кластеризации Gostev I. M. Shape Analysis 22

Алгоритм k-внутригрупповых средних (k-means) ? Этот алгоритм представляет собой пошаговое (итерационное) нахождение центров кластеров и разбиение обучающей выборки на кластеры до тех пор, пока некоторый функционал Q не перестанет уменьшаться. Примеры клеток Вороного в метриках Евклида, манхэттенской и Канберра. Gostev I. M. Shape Analysis 23

Алгоритмы расстановки центров кластеров (1) Алгоритм простейшей расстановки центров кластеров Gostev I. M. Shape Analysis 24

Алгоритмы расстановки центров кластеров (2) Алгоритм максиминного расстояния Gostev I. M. Shape Analysis 25

Элементарные методы идентификации функций • По числу точек • По площади • По компактности • По габаритам • По центральным моментам • На основе математической корреляции Gostev I. M. Shape Analysis 26

Понятие компактности Теоретическая компактность инвариантна к сдвигам, поворотам и масштабу Для окружности: Для правильного n-угольника: Gostev I. M. Shape Analysis 27
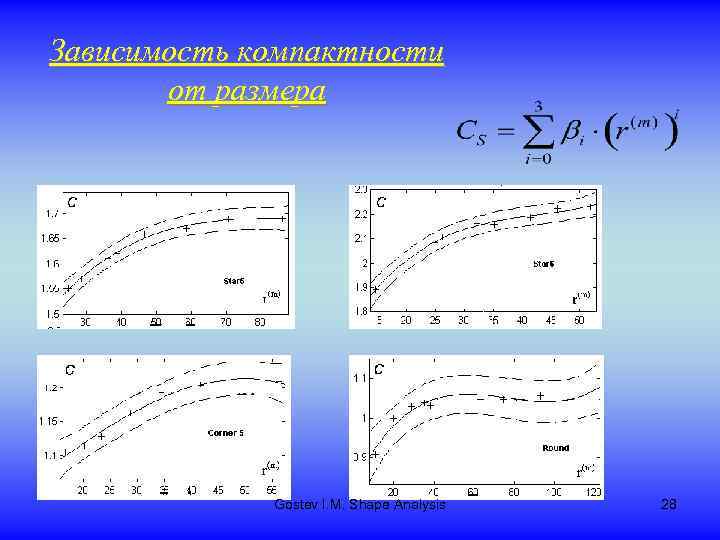
Зависимость компактности от размера Gostev I. M. Shape Analysis 28

Понятие контурных функций - функция сортировки множества по углу в порядке его возрастания. - функция интерполяции точек объекта Gostev I. M. Shape Analysis 29
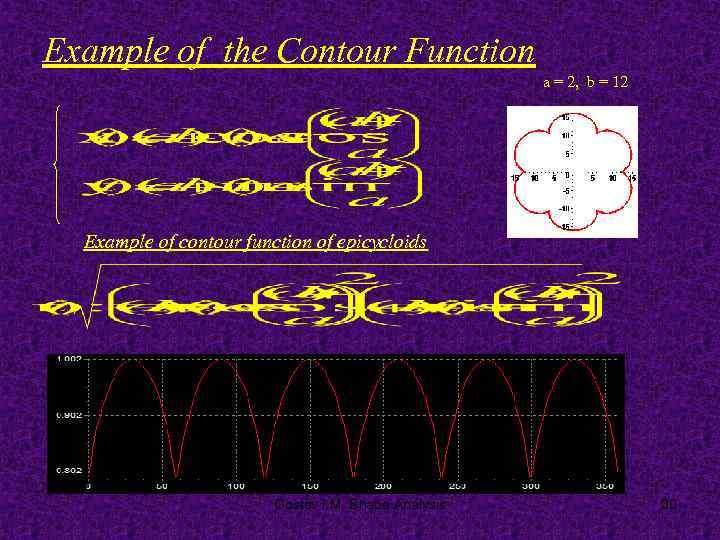
Example of the Contour Function a = 2, b = 12 Example of contour function of epicycloids Gostev I. M. Shape Analysis 30
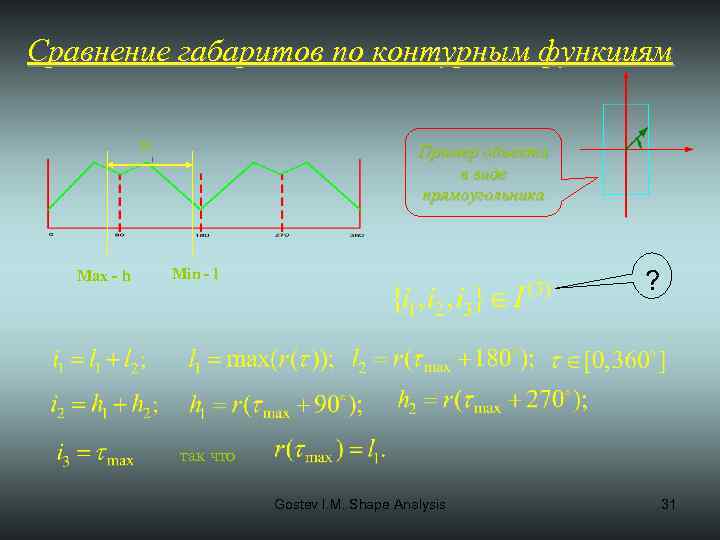
Сравнение габаритов по контурным функциям 90 Max - h Пример объекта в виде прямоугольника Min - l ? так что Gostev I. M. Shape Analysis 31

Понятие эталона Эталон - это вербальное описание совокупности групп параметров, которые однозначно характеризуют некоторый объект. К таким группам относятся: ü методы и условия получения объекта; ü координатные значения параметров объекта; ü методы, применяемые для идентификации и их порядок; ü допуски, определенные для каждого метода; Gostev I. M. Shape Analysis 32

Понятие контурных функций - функция сортировки множества по углу в порядке его возрастания. - функция интерполяции точек объекта Gostev I. M. Shape Analysis 33
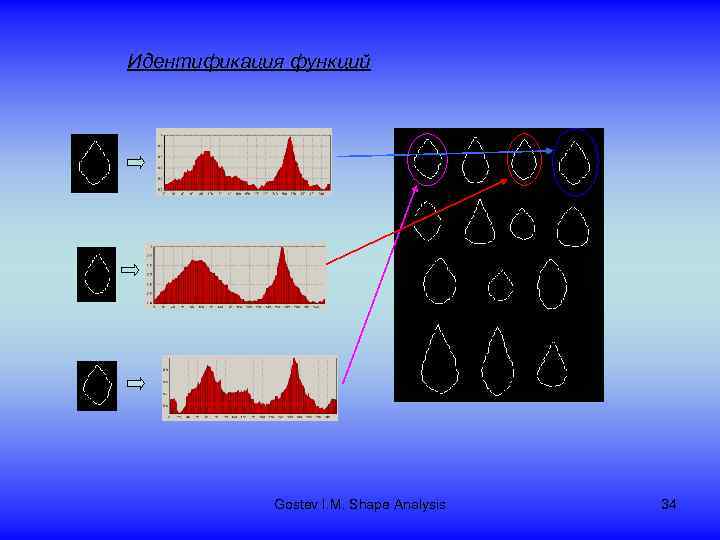
Идентификация функций Gostev I. M. Shape Analysis 34

Геометрическая корреляция 1 (ГК 1) Определим как функцию разности значений и где Определим функцию отклонения где Функция распознавания на основе геометрической корреляции № 1 где Gostev I. M. Shape Analysis 35

Геометрическая корреляция 2 (ГК 2) Определим функцию как среднее отклонение от где Функция распознавания на основе геометрической корреляции № 2 где Gostev I. M. Shape Analysis 36
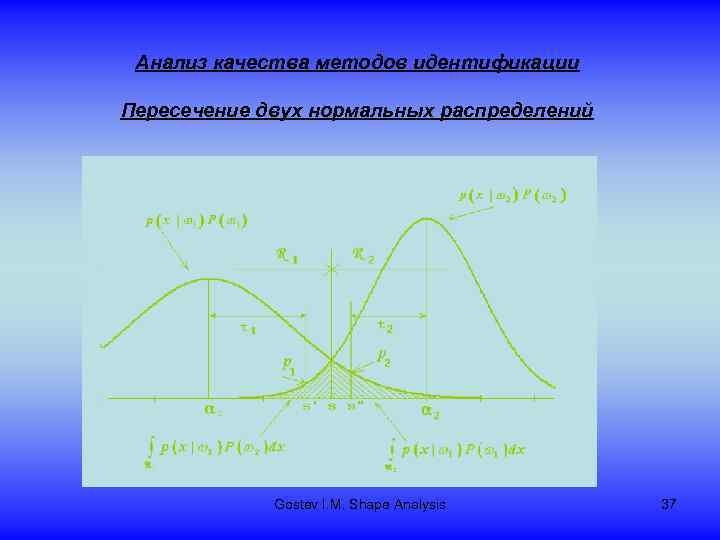
Анализ качества методов идентификации Пересечение двух нормальных распределений Gostev I. M. Shape Analysis 37
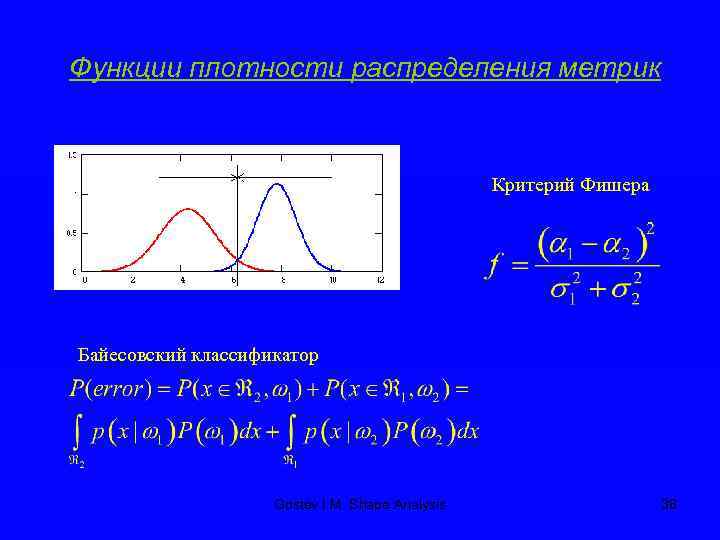
Функции плотности распределения метрик Критерий Фишера Байесовский классификатор Gostev I. M. Shape Analysis 38
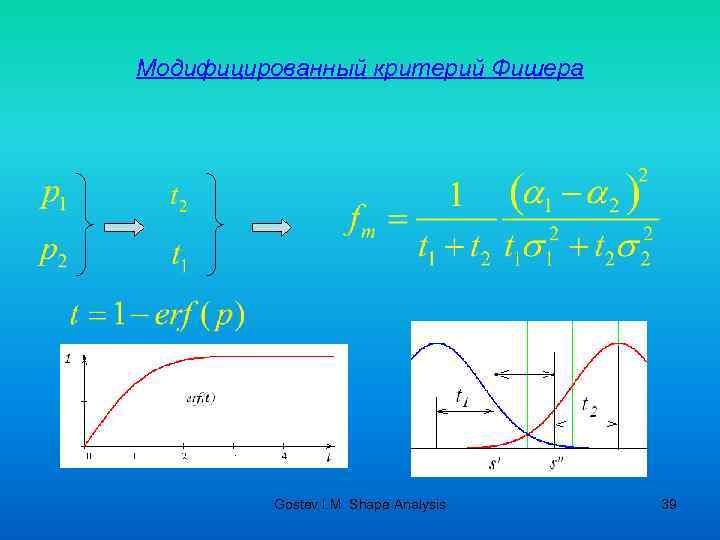
Модифицированный критерий Фишера Gostev I. M. Shape Analysis 39
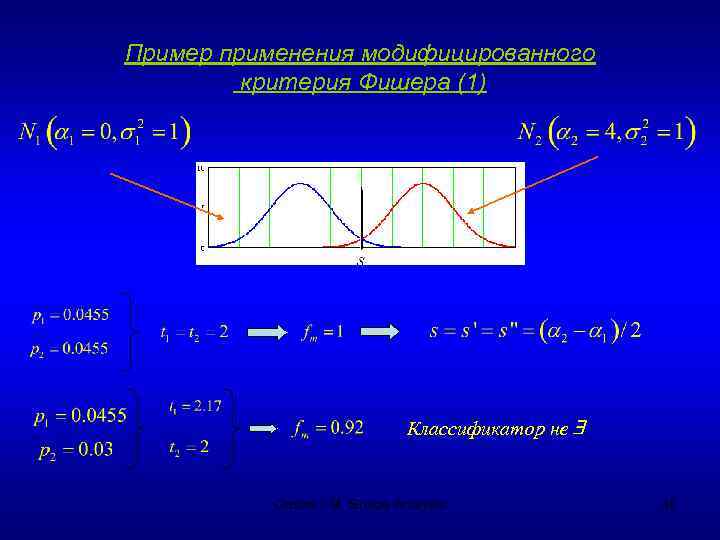
Пример применения модифицированного критерия Фишера (1) Классификатор не Gostev I. M. Shape Analysis 40
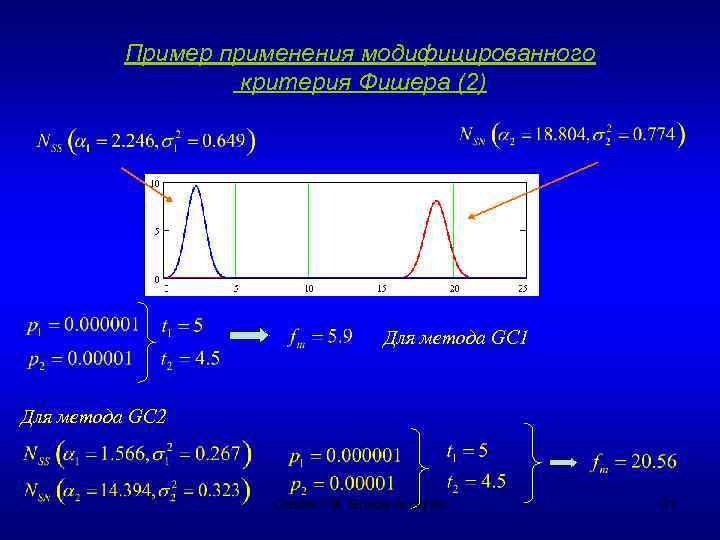
Пример применения модифицированного критерия Фишера (2) Для метода GC 1 Для метода GC 2 Gostev I. M. Shape Analysis 41
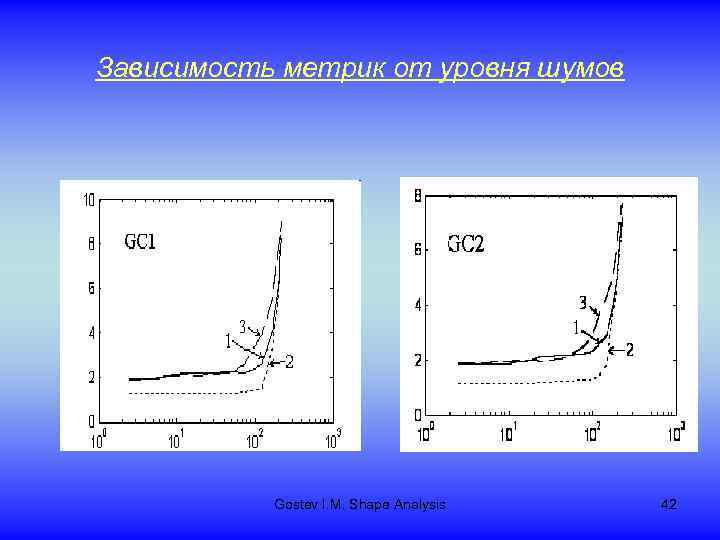
Зависимость метрик от уровня шумов Gostev I. M. Shape Analysis 42
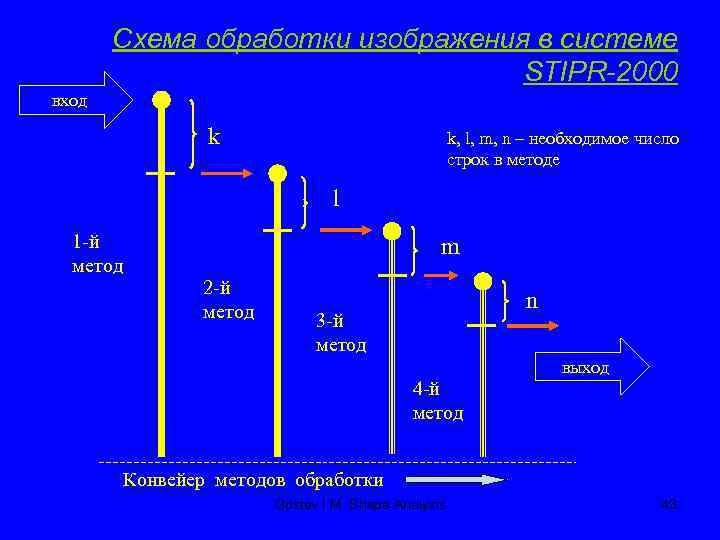
Схема обработки изображения в системе STIPR-2000 вход k k, l, m, n – необходимое число строк в методе l 1 -й метод m 2 -й метод n 3 -й метод выход 4 -й метод Конвейер методов обработки Gostev I. M. Shape Analysis 43
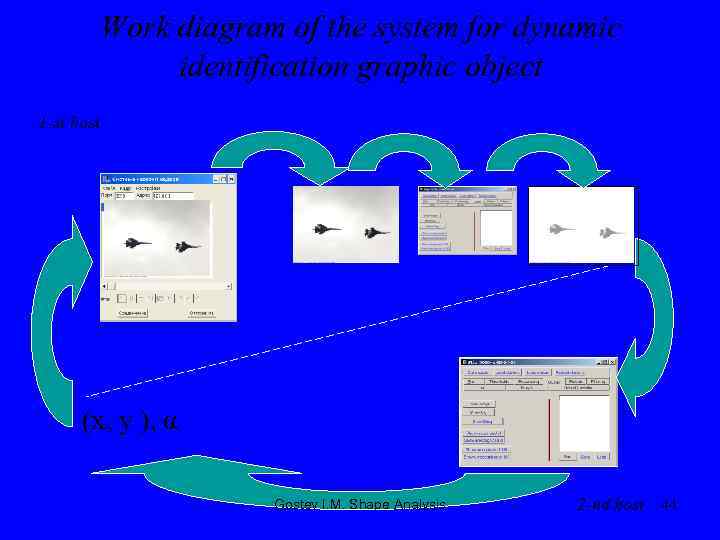
Work diagram of the system for dynamic identification graphic object 1 -st host (x, y ), α Gostev I. M. Shape Analysis 2 -nd host 44
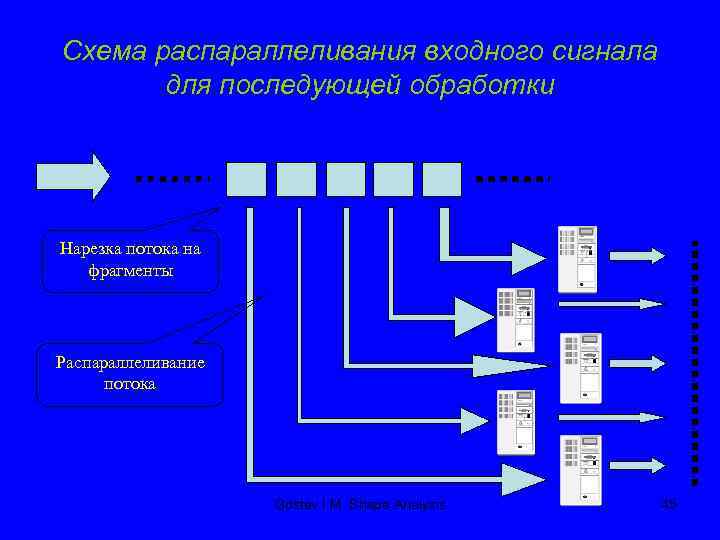
Схема распараллеливания входного сигнала для последующей обработки Нарезка потока на фрагменты Распараллеливание потока Gostev I. M. Shape Analysis 45

Gostev I. M. Shape Analysis 46

Классификация по компактности Теоретически самой компактной фигурой является окружность, для которой значение компактности равно 4. Однако на практике удобнее считать значение компактности окружности равным 1, то есть поделённым на коэффициент равный 4. Тогда пределы изменения компактности будут находиться в интервале [1, ∞] Gostev I. M. Shape Analysis 47
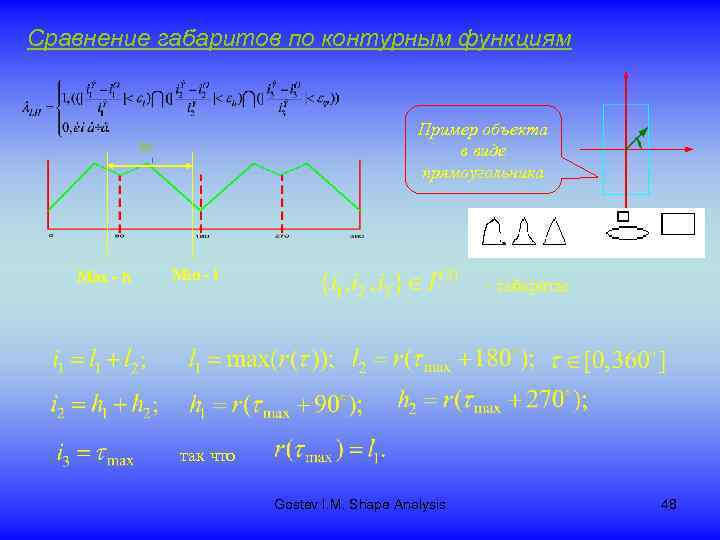
Сравнение габаритов по контурным функциям Пример объекта в виде прямоугольника 90 Max - h Min - l - габариты так что Gostev I. M. Shape Analysis 48

Eccentricity Gostev I. M. Shape Analysis 49
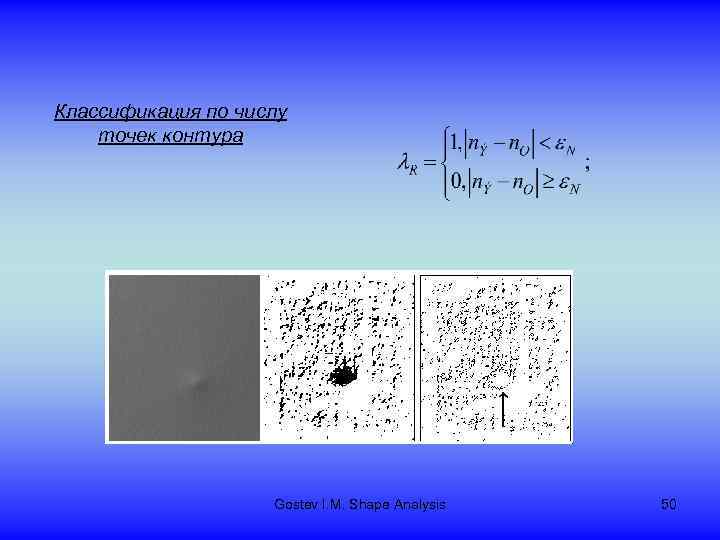
Классификация по числу точек контура Gostev I. M. Shape Analysis 50
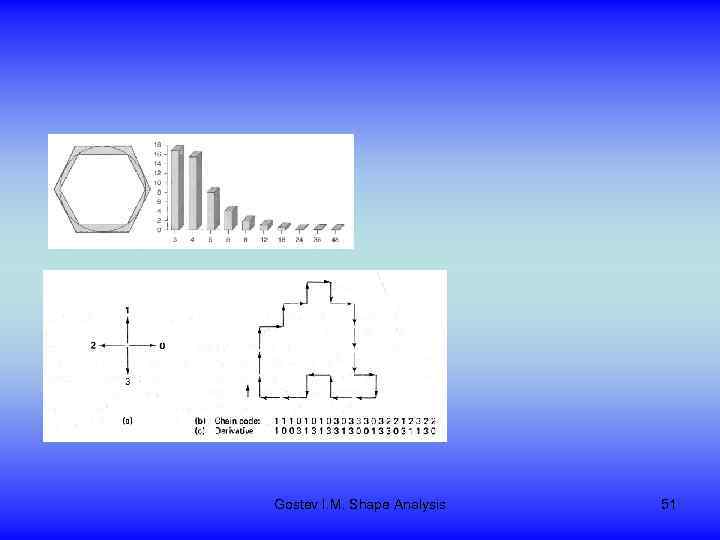
Gostev I. M. Shape Analysis 51
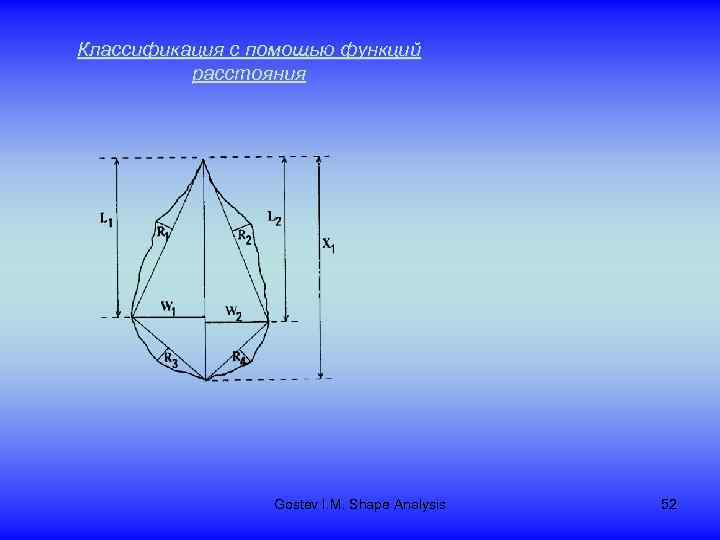
Классификация с помощью функций расстояния Gostev I. M. Shape Analysis 52

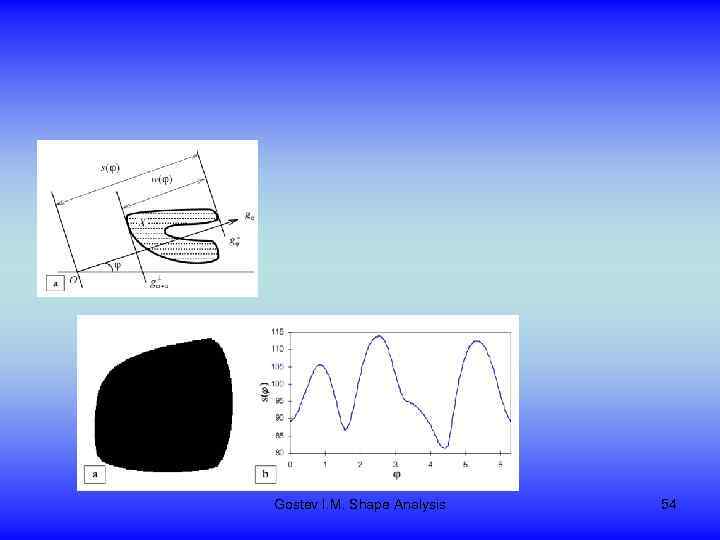
Сигнатурный анализ Gostev I. M. Shape Analysis 53
Gostev I. M. Shape Analysis 54
Распознавание образов.ppt