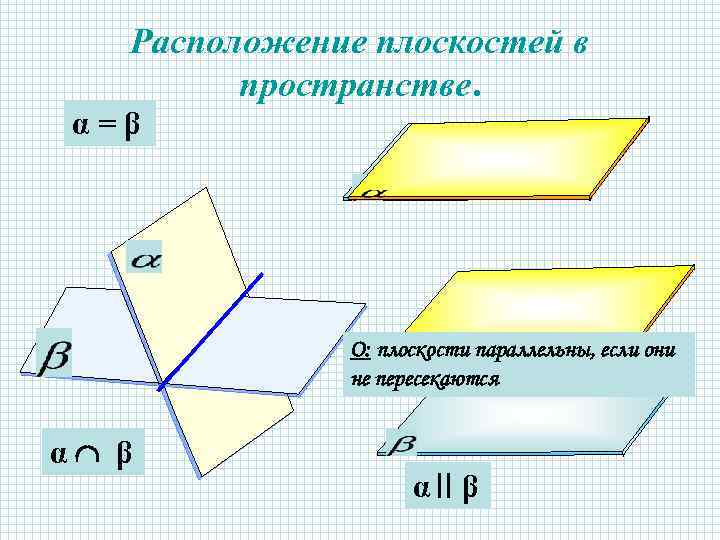
Расположение плоскостей в пространстве. α=β О: плоскости параллельны, если они не пересекаются α β α β
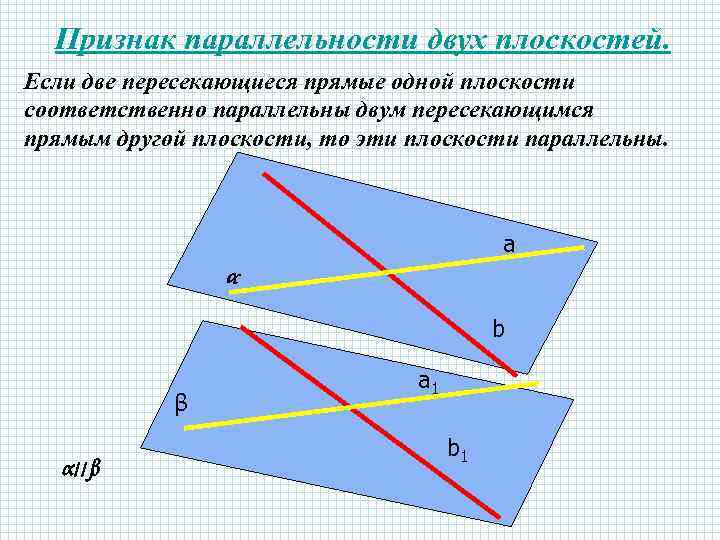
Признак параллельности двух плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. a α b β α ׀׀ β a 1 b 1
Дано: а b = M, a , b . a 1 b 1, a 1 , b 1 . a a 1, b b 1. Доказать: 1. Пусть = с. Методом от противного Тогда а (по признаку парал-ти прямой и плоскости), а , = с, Доказательство: значит а с. 2. b , b , = с, значит b с. 3. Имеем, что через точку М проходят две прямые а и b, параллельные прямой с, чего быть на может. Значит .
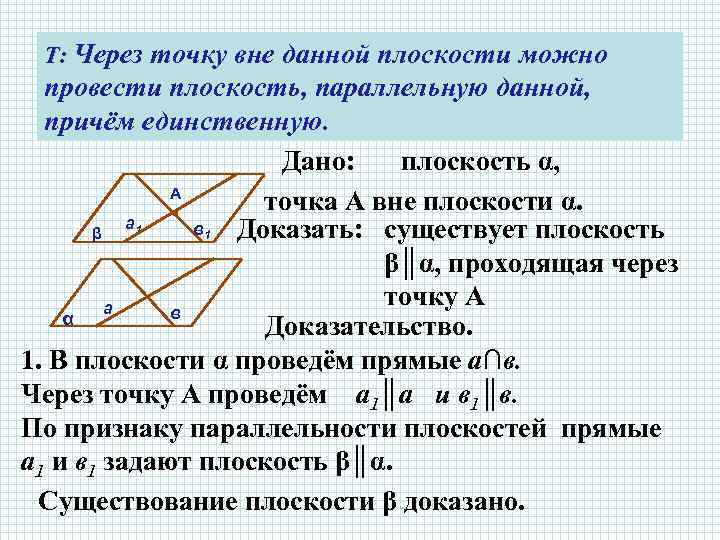
Т: Через точку вне данной плоскости можно провести плоскость, параллельную данной, причём единственную. Дано: плоскость α, А точка А вне плоскости α. • а 1 в 1 Доказать: существует плоскость β β║α, проходящая через точку А а в α Доказательство. 1. В плоскости α проведём прямые а∩в. Через точку А проведём а 1║а и в 1║в. По признаку параллельности плоскостей прямые а 1 и в 1 задают плоскость β║α. Существование плоскости β доказано.
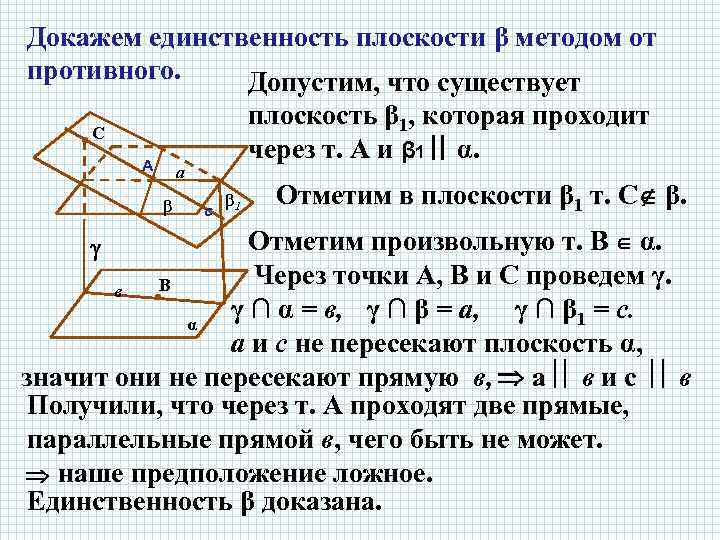
Докажем единственность плоскости β методом от противного. Допустим, что существует плоскость β 1, которая проходит через т. А и β 1 α. • С А а • β с β 1 Отметим в плоскости β 1 т. С β. Отметим произвольную т. В α. Через точки А, В и С проведем γ. В в • γ ∩ α = в, γ ∩ β = а, γ ∩ β 1 = с. α а и с не пересекают плоскость α, значит они не пересекают прямую в, а в и с в Получили, что через т. А проходят две прямые, параллельные прямой в, чего быть не может. наше предположение ложное. Единственность β доказана.
Свойство параллельных плоскостей. а b Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Дано: α β, α = a β =b Доказать: a b Доказательство: 1. a , b 2. Пусть a и b не параллельны методом от противного, тогда a b = М 3. M α, M β α β = с (А 2) Получили противоречие с условием. Значит a b ч. т. д.
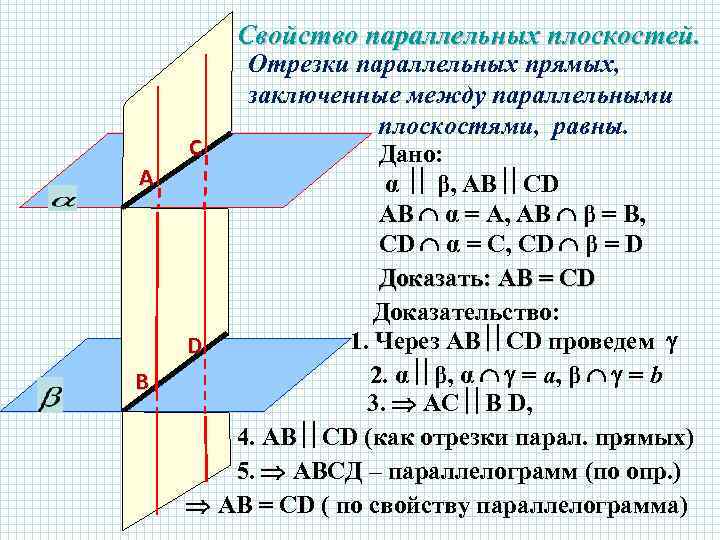
Свойство параллельных плоскостей. А В Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. С Дано: α β, АВ СD АВ α = А, АВ β = В, СD α = С, СD β = D Доказать: АВ = СD Доказательство: 1. Через АВ СD проведем D 2. α β, α = a, β = b 3. АС В D, 4. АВ СD (как отрезки парал. прямых) 5. АВСД – параллелограмм (по опр. ) АВ = СD ( по свойству параллелограмма)
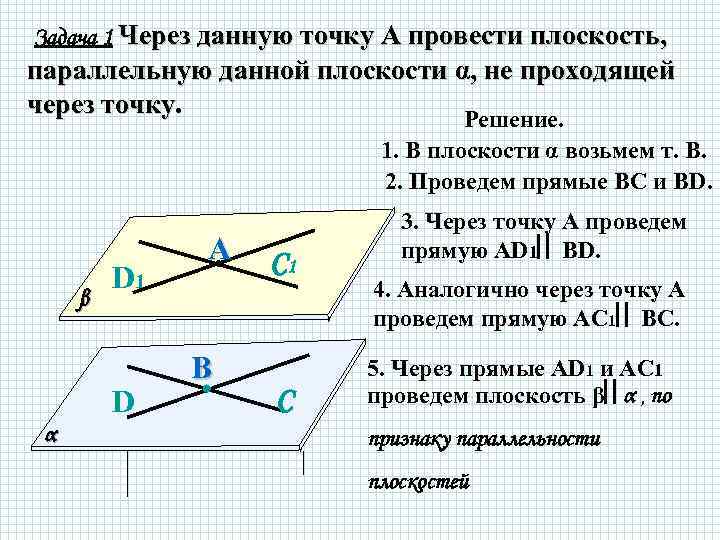
Задача 1 Через данную точку А провести плоскость, параллельную данной плоскости α, не проходящей через точку. Решение. 1. В плоскости α возьмем т. В. 2. Проведем прямые ВС и ВD. β D 1 D α А • В • С 1 С 3. Через точку А проведем прямую АD 1 ВD. 4. Аналогично через точку А проведем прямую АС 1 ВС. 5. Через прямые АD 1 и АС 1 проведем плоскость β α , по признаку параллельности плоскостей
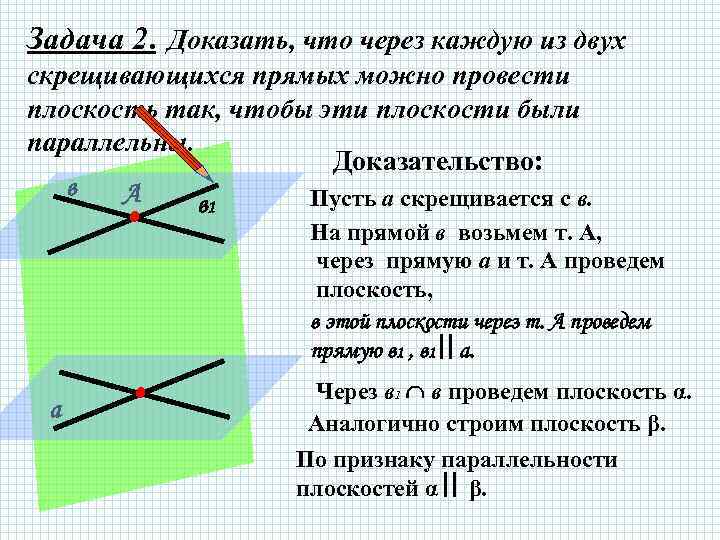
Задача 2. Доказать, что через каждую из двух скрещивающихся прямых можно провести плоскость так, чтобы эти плоскости были параллельны. Доказательство: в А Пусть а скрещивается с в. в 1 . а . На прямой в возьмем т. А, через прямую а и т. А проведем плоскость, в этой плоскости через т. А проведем прямую в 1 , в 1 a. Через в 1 в проведем плоскость α. Аналогично строим плоскость β. По признаку параллельности плоскостей α β.
ВЫВОДЫ 1. 2. 3. 4. 5. 6. 7. В пространстве плоскости могут совпадать, пересекаться или быть параллельными. Две плоскости, не имеющие ни одной общей точки, называются параллельными. Признаком параллельности плоскостей является соответственная параллельность двух пар пересекающихся прямых, находящихся в данных плоскостях. Через точку вне данной плоскости можно провести единственную плоскость, параллельную данной. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и вторую.
Скачать презентацию Расположение плоскостей в пространстве α β О плоскости параллельны
Первому МО параллельность плокостей.ppt