Скачать презентацию Распадающиеся уравнения Урок 1 Определение
3321_Mod(2).ppt
- Количество слайдов: 11
«Распадающиеся уравнения. » Урок 1
Определение Уравнение вида где и многочлены относительно , называют распадающимися уравнениями. - Множество всех корней распадающегося уравнения есть объединение множеств всех корней двух уравнений и.
Пример 1 Решить уравнение Решение Произведение двух чисел равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю, а другой при этом не теряет смысла. или
Пример 1 Решить уравнение Решение по теореме обратной теореме Виета имеем: Ответ: -2, 1, 2, 3.
Пример 2 Решить уравнение Решение 1. Разложим левую часть уравнения на множители, используя формулу разности кубов: корней нет Ответ: 1.
Пример 3 Решить уравнение Решение 1. Разложим левую часть уравнения на множители: Произведение двух чисел равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю, а другой при этом не теряет смысла.
Пример 3 Решить уравнение Решение 2. Решим полученное распадающееся уравнение: корней нет Ответ: 1; -1
Пример 4 Решить уравнение Решение или значит уравнение имеет два действительных корня По теореме обратной теореме Виета имеем: Ответ:
Приведите пример распадающегося уравнения и объясните, как его решить. Что значит «уравнение распадается на два уравнения» ? При каких значениях равенство ? Верно ли, что если и выполняется , то Равносильны ли уравнения Является ли число 0 корнем уравнения ? и ? ?
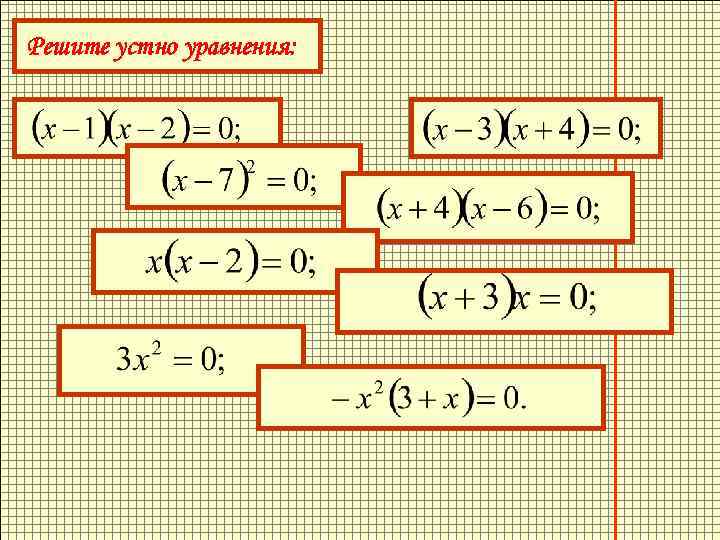Решите устно уравнения:
