РАСЧЕТ ТОНКОСТЕННЫХ СОСУДОВ И РЕЗЕРВУАРОВ Тема 15

РАСЧЕТ ТОНКОСТЕННЫХ СОСУДОВ И РЕЗЕРВУАРОВ Тема 15

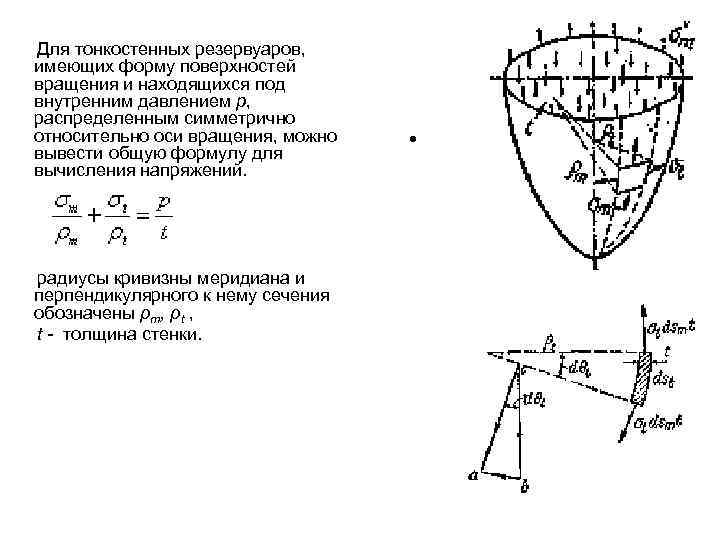Для тонкостенных резервуаров, имеющих форму поверхностей вращения и находящихся под внутренним давлением р, распределенным симметрично относительно оси вращения, можно вывести общую формулу для вычисления напряжений. радиусы кривизны меридиана и перпендикулярного к нему сечения обозначены ρm, ρt , t - толщинa стенки. •

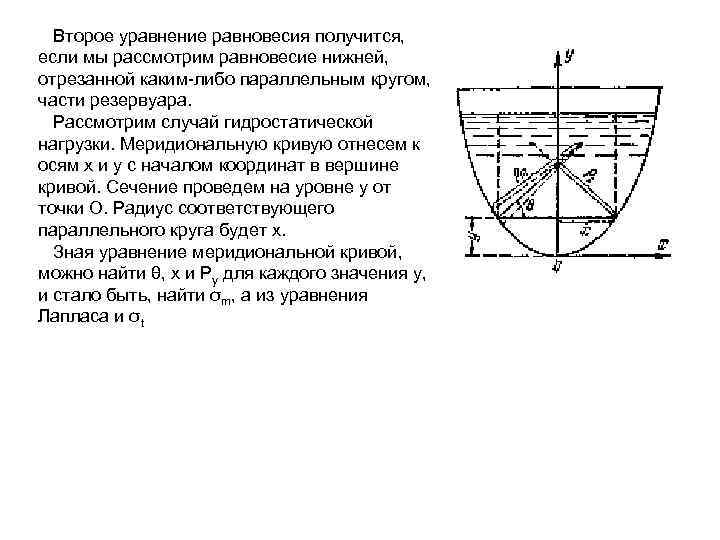Второе уравнение равновесия получится, если мы рассмотрим равновесие нижней, отрезанной каким-либо параллельным кругом, части резервуара. Рассмотрим случай гидростатической нагрузки. Меридиональную кривую отнесем к осям х и у с началом координат в вершине кривой. Сечение проведем на уровне у от точки О. Радиус соответствующего параллельного круга будет х. Зная уравнение меридиональной кривой, можно найти θ, х и Рy для каждого значения у, и стало быть, найти σm, а из уравнения Лапласа и σt

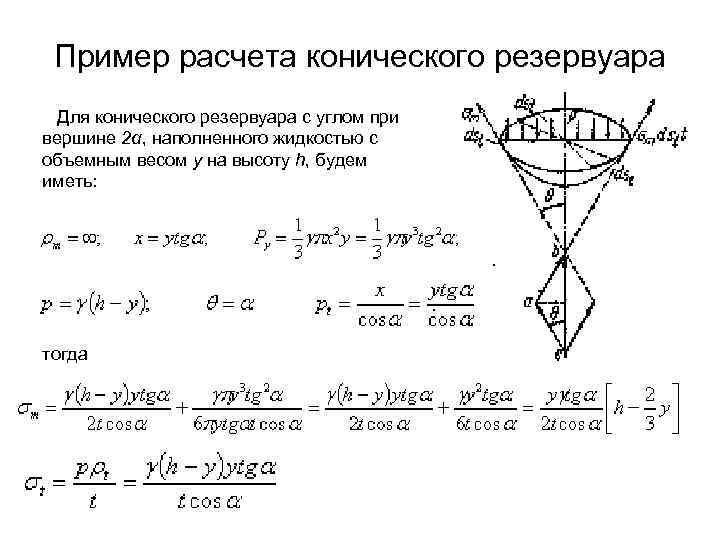Пример расчета конического резервуара Для конического резервуара с углом при вершине 2α, наполненного жидкостью с объемным весом у на высоту h, будем иметь: тогда

Пример расчета сферического резервуара Для сферического сосуда радиусом r 0, находящегося под внутренним давлением p 0, по симметрии ; тогда из уравнения (Лапласа), так как получаем

Если меридиональная кривая будет иметь переломы с разрывом непрерывности угла θ, то равновесие тонкой оболочки у места перелома может быть обеспечено лишь наличием реакций, приложенных к оболочке по окружности в этом месте. Появление таких реакций обеспечивается устройством специальных колец, способных брать на себя усилия, возникающие в них в связи с неуравновешенностью напряжений σm по обе стороны точки перелома.