Расчет статически неопределимых рам методом перемещений Если

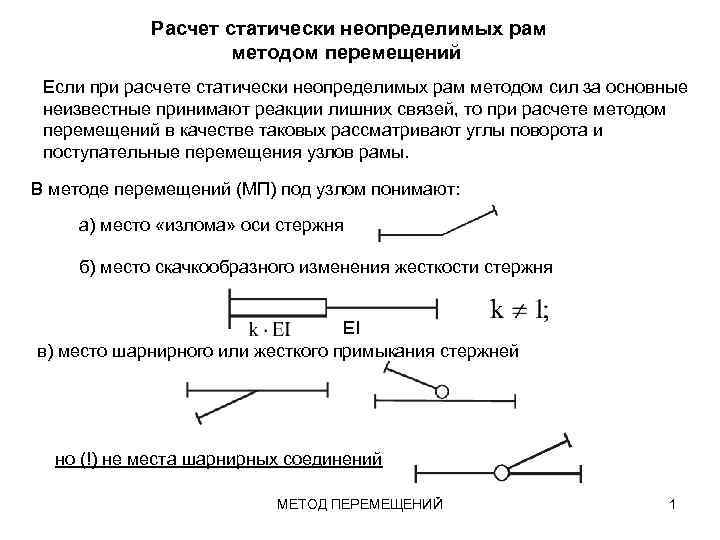Расчет статически неопределимых рам методом перемещений Если при расчете статически неопределимых рам методом сил за основные неизвестные принимают реакции лишних связей, то при расчете методом перемещений в качестве таковых рассматривают углы поворота и поступательные перемещения узлов рамы. В методе перемещений (МП) под узлом понимают: а) место «излома» оси стержня б) место скачкообразного изменения жесткости стержня EI в) место шарнирного или жесткого примыкания стержней но (!) не места шарнирных соединений МЕТОД ПЕРЕМЕЩЕНИЙ 1

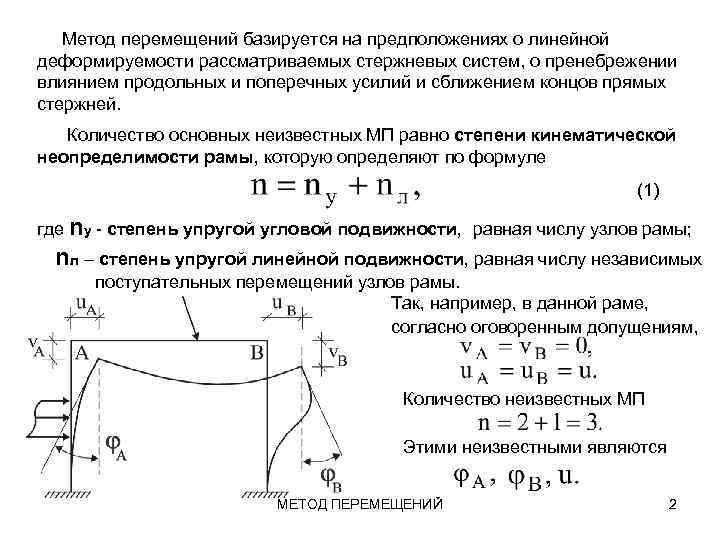Метод перемещений базируется на предположениях о линейной деформируемости рассматриваемых стержневых систем, о пренебрежении влиянием продольных и поперечных усилий и сближением концов прямых стержней. Количество основных неизвестных МП равно степени кинематической неопределимости рамы, которую определяют по формуле (1) где nу - степень упругой угловой подвижности, равная числу узлов рамы; nл – степень упругой линейной подвижности, равная числу независимых поступательных перемещений узлов рамы. Так, например, в данной раме, согласно оговоренным допущениям, Количество неизвестных МП Этими неизвестными являются МЕТОД ПЕРЕМЕЩЕНИЙ 2

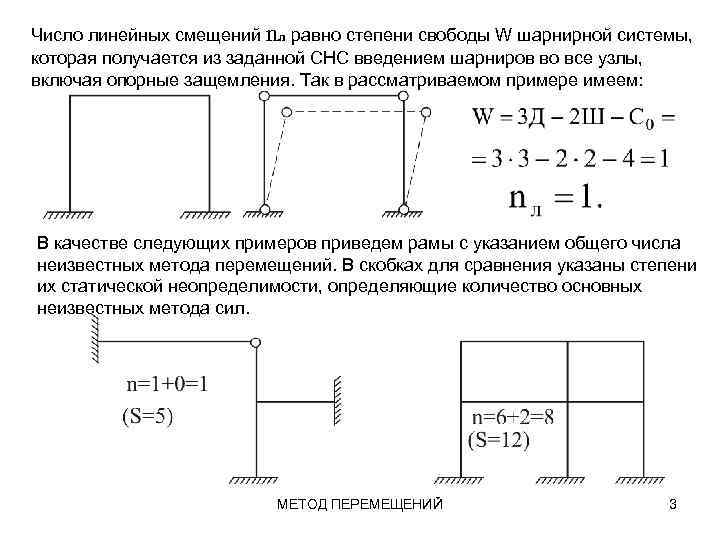Число линейных смещений nл равно степени свободы W шарнирной системы, которая получается из заданной СНС введением шарниров во все узлы, включая опорные защемления. Так в рассматриваемом примере имеем: В качестве следующих примеров приведем рамы с указанием общего числа неизвестных метода перемещений. В скобках для сравнения указаны степени их статической неопределимости, определяющие количество основных неизвестных метода сил. МЕТОД ПЕРЕМЕЩЕНИЙ 3

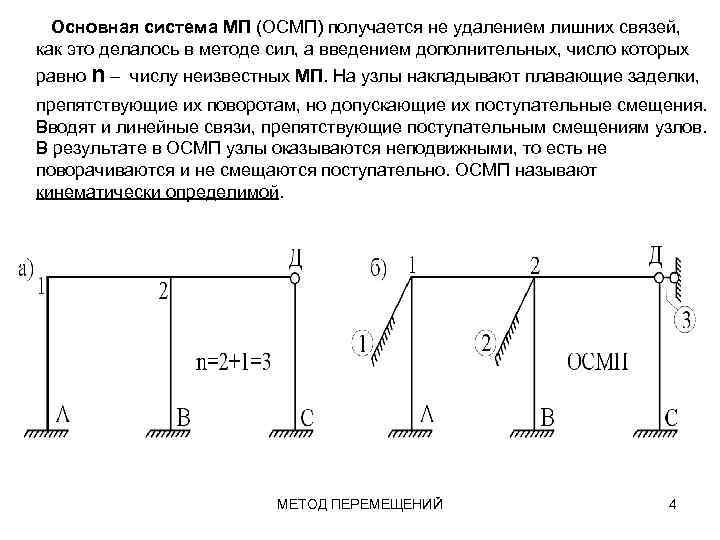Основная система МП (ОСМП) получается не удалением лишних связей, как это делалось в методе сил, а введением дополнительных, число которых равно n – числу неизвестных МП. На узлы накладывают плавающие заделки, препятствующие их поворотам, но допускающие их поступательные смещения. Вводят и линейные связи, препятствующие поступательным смещениям узлов. В результате в ОСМП узлы оказываются неподвижными, то есть не поворачиваются и не смещаются поступательно. ОСМП называют кинематически определимой. МЕТОД ПЕРЕМЕЩЕНИЙ 4

Таким образом ОСМП представляет собой набор стандартных стержней постоян жесткости двух типов: 1 - с двумя заделками по концам; 2 - с заделкой на одном конце и шарниром на другом. В этих стандартного вида стержнях нетрудно предварительно определить внутренние усилия от действия часто встречающихся видов нагрузки и смещения опор, а результаты свести в таблицы. Примем обозначения: Zi – искомое неизвестное, равное поступательному или угловому смещению i-й введенной связи; Ri. F, Riк, riк – реакции в указанных связях соответственно от действия заданной нагрузки, смещения Zк и смещения Zк = 1. Так как система линейно деформируема, то (2) МЕТОД ПЕРЕМЕЩЕНИЙ 5

Положим, что рассматриваемая рама n – раз кинематически неопределима. Образуем ОСМП, загрузим ее, а узлам сообщим перемещения Zк, равные смещениям соответствующих узлов исходной системы. Как результат, во введенных связях ОСМП возникнут реактивные усилия Rк, которые согласно принятым допущениям можно представить в виде: (3) В заданной системе этих связей нет, а следовательно равны нулю и соответствующие реакции. Отсюда следует, что рассматриваемая ОСМП лишь тогда будет эквивалентна заданной, когда выполняются равенства нулю реакций (3) во введенных связях: (4) Переписав (4) с учетом (2), (3), приходим к системе канонических уравнений метода перемещений, определяющей неизвестные Zк: - - - - - - - - - - - - (5) МЕТОД ПЕРЕМЕЩЕНИЙ 6

Итак, в основе уравнений МП лежит, если угодно, отрицание реактивных усилий во введенных связях ОСМП, в противоположность тому, что в основе уравнений метода сил лежит отрицание перемещений в ОСМС точек приложения и по направлению основных неизвестных усилий. Рассмотрим статически неопределимую балку в двух состояниях: 1 и 2. Положим, что в первом состоянии имеет место единичное смещение опорной связи i, а во втором – опорной связи j. Эти перемещения вызовут реакции связей На основании теоремы о взаимности работ двух состояний системы имеем: Отсюда следует: Тем самым получено доказательство теоремы Рэлея о взаимности Реакций и, как следствие, доказано равенство коэффициентов канонических Уравнений МП, расположенных симметрично относительно главной диагонали матрицы коэффициентов. МЕТОД ПЕРЕМЕЩЕНИЙ 7

Для определения коэффициентов канонических уравнений МП необходимо знать величины внутренних усилий в стандартных стержнях, составляющих ОСМП, которые возникают от смещения их концов и от нагрузки. Уравнение оси изогнутого стержня с учетом известной зависимости = q, запишем в виде (6) Его решение : (7) Отсюда следует МЕТОД ПЕРЕМЕЩЕНИЙ 8

Если начальные параметры, то (7) можно представить так: (8) Рассмотрим, например, стержень с обоими заделанными концами, которым сообщим перемещения. Условия на правом конце x = l: С их помощью нетрудно определить: (9) МЕТОД ПЕРЕМЕЩЕНИЙ 9

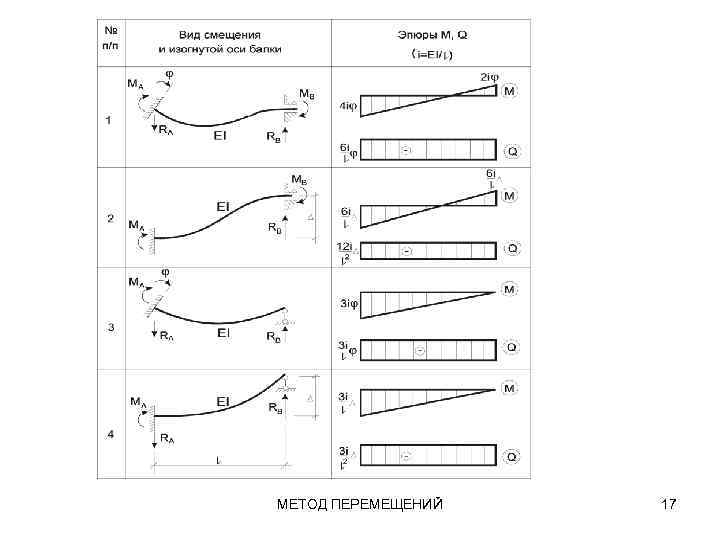
Так, например, если принять то из (9) нетрудно получить: Аналогично можно было бы получить решения и для других вариантов закрепления концов стержня, смещения и нагрузки. Соответствующие значения реакций в связях и эпюры М в однопролетных статически неопределимых элементах основной системы сведены в таблицы метода перемещений. МЕТОД ПЕРЕМЕЩЕНИЙ 10

Для определения коэффициентов и свободных членов системы канонических уравнений МП необходимо предварительно построить эпюры моментов в основной системе от заданной нагрузки – МF и от единичных смещений введенных связей – Mi. Построение их производится с помощью упомянутых таблиц метода перемещений. Коэффициенты и свободные члены , представляющие собой реактивные моменты во введенных защемлениях, определяются из условия равновесия узлов реактивные усилия во введенных линейных связях определяют из условия равновесия части рамы. Реактивное усилие считают положительным, если направление его действия совпадает с принятым направлением поворота или линейного смещения узла Решение системы канонических уравнений МП, то есть определение ZK, позволяет построить эпюру М в заданной системе: (10) Основной проверкой правильности построенной эпюры является статическая проверка равновесия узлов рамы. Можно воспользоваться и кинематической проверкой эпюры М так, как это делается в методе сил. МЕТОД ПЕРЕМЕЩЕНИЙ 11

ПРИМЕР Построить эпюру М. Степень статической неопределимости рамы Степень кинематической неопределимости рамы Решаем задачу методом перемещений. Каноническое уравнение МП Погонные жесткости стержней рамы Образуем основную систему метода перемещений (ОСМП) МЕТОД ПЕРЕМЕЩЕНИЙ 12

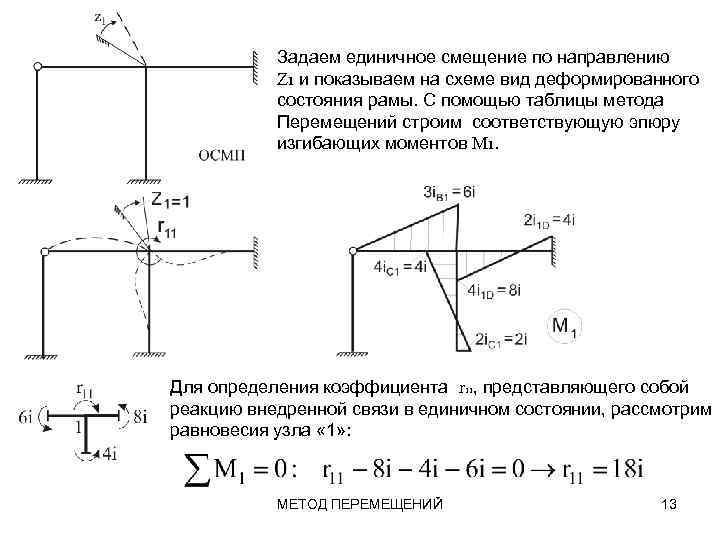Задаем единичное смещение по направлению Z 1 и показываем на схеме вид деформированного состояния рамы. С помощью таблицы метода Перемещений строим соответствующую эпюру изгибающих моментов М 1. Для определения коэффициента r 11, представляющего собой реакцию внедренной связи в единичном состоянии, рассмотрим равновесия узла « 1» : МЕТОД ПЕРЕМЕЩЕНИЙ 13

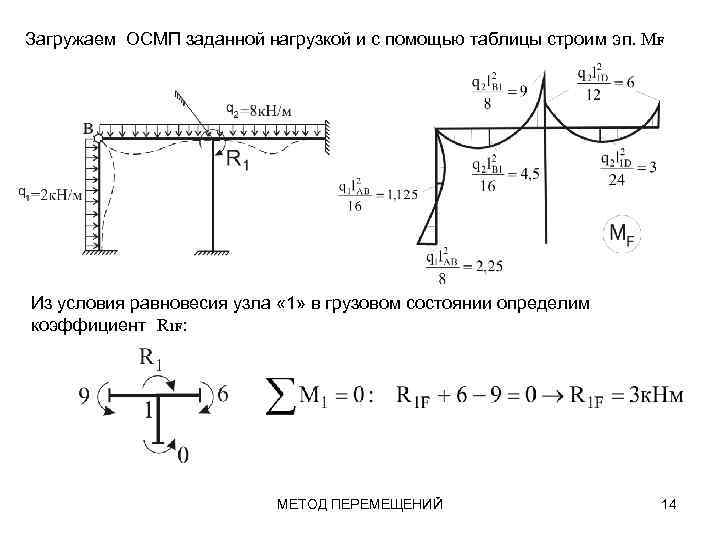Загружаем ОСМП заданной нагрузкой и с помощью таблицы строим эп. МF Из условия равновесия узла « 1» в грузовом состоянии определим коэффициент R 1 F: МЕТОД ПЕРЕМЕЩЕНИЙ 14

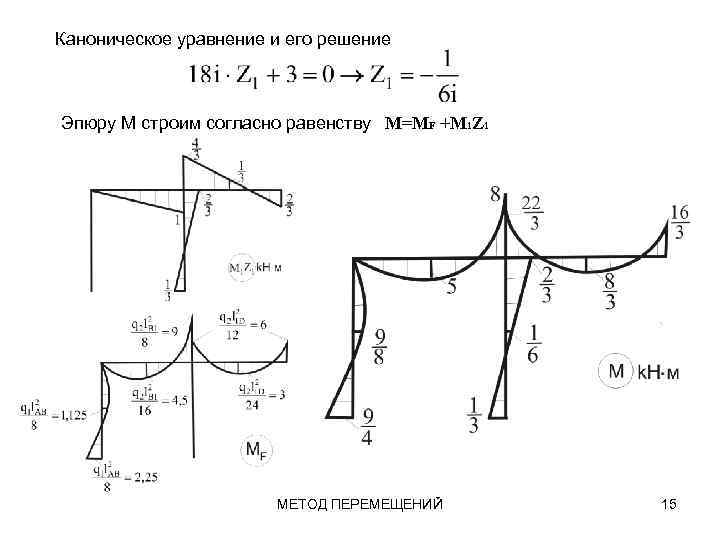Каноническое уравнение и его решение Эпюру М строим согласно равенству M=MF +M 1 Z 1 МЕТОД ПЕРЕМЕЩЕНИЙ 15

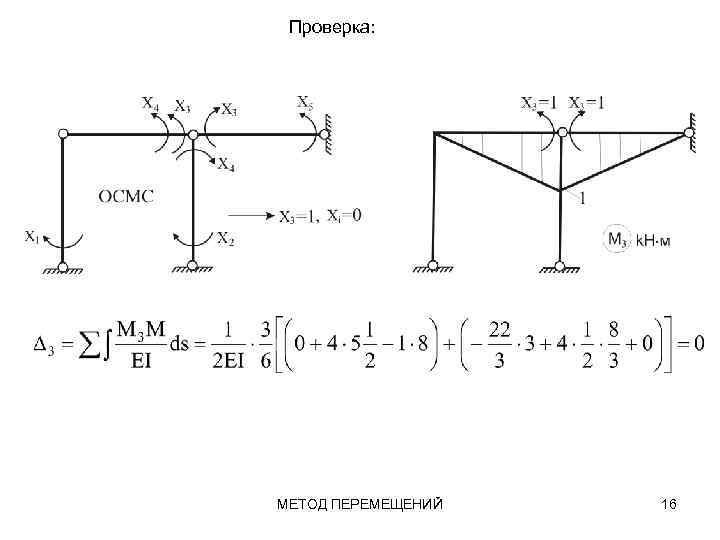Проверка: МЕТОД ПЕРЕМЕЩЕНИЙ 16

МЕТОД ПЕРЕМЕЩЕНИЙ 17

МЕТОД ПЕРЕМЕЩЕНИЙ 18