Расчет на прочность стенок самолетных конструкций Стенки

Расчет на прочность стенок самолетных конструкций

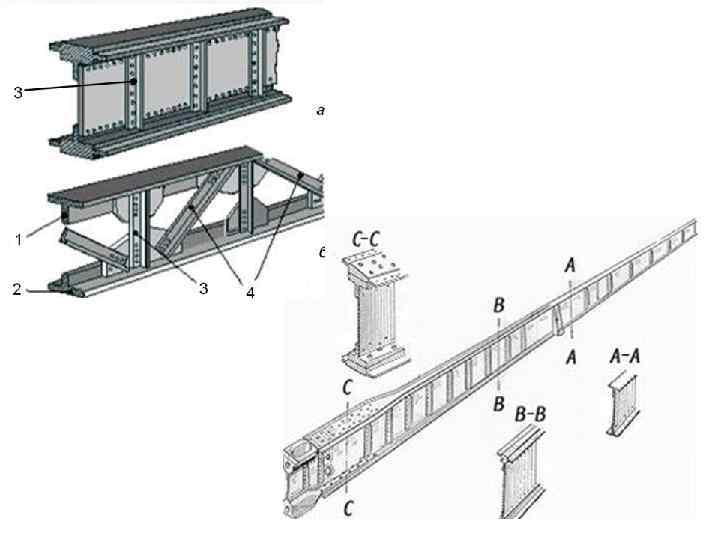
Стенки в конструкции Стенкой мы называем плоскую или гофрированную пластинку, работающую, как правило, на сдвиг. Стенки встречаются в элементах конструкции самолёта весьма часто: стенки лонжеронов и нервюр крыла, оперения, элементов управления и механизации крыла. Стенки по своей форме и методу соединения с поясами подразделяются на Свободные Подкрепленные Цельнофрезерованные Клёпаные Сотовые Гофрированные С отверстиями облегчения Подкрепленные стойками Подкреплённые рифтами(выштамповками) Ферменные Рамные

Стенки рассматриваются, как элементы конструкции, работающие преимущественно на сдвиг. Поэтому главный нагружающий фактор для них – поток касательных усилий. Если силовой расчет конструкции выполнен с применением МКЭ, то поток касательных усилий получается как результат расчета напрямую, т. е. в каждом конкретном конечном элементе мы можем найти поток прямо из таблицы результатов. Если же мы ведем ручной расчет, то для стенок нервюр, лонжеронов, различных балок необходимо в каждом интересующем нас сечении получить перезывающую силу, а затем определить поток касательных усилий и касательные напряжения. Последовательность расчета стенок на прочность такова: 1. Определить поток касательных усилий 2. Определить касательные напряжения 3. Определить критические напряжения 4. Определить разрушающие касательные напряжения 5. Определить нагрузки на соединение стенки с поясами 6. Рассчитать несущую способность соединений на срез и смятие 7. Определить запасы прочности по стенке и по её креплению.

Углы β 1 и β 2 называют углами конусности, которые необходимо учитывать при расчете срезающей силы с учетом разгрузки: Qx = Q – M / h * tg(β 1+β 2) Тогда касательный поток: q xy = Qx / h И касательные напряжения: Τ = q xy / δ

Журавского(турксиб)

F

=q / h

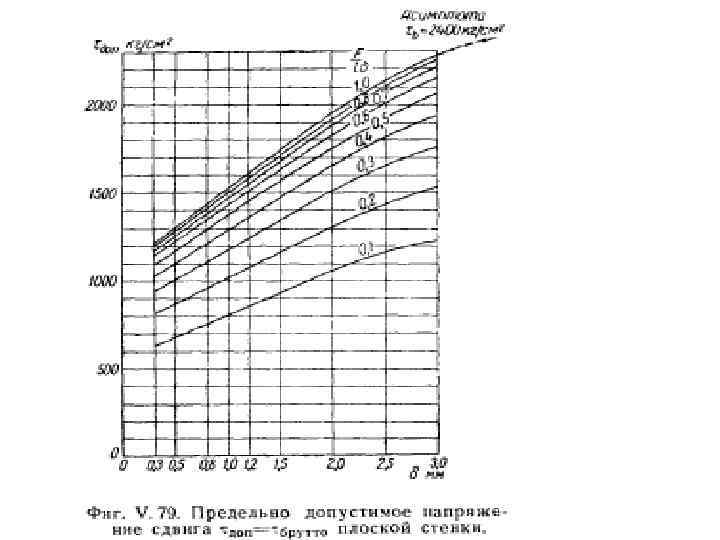
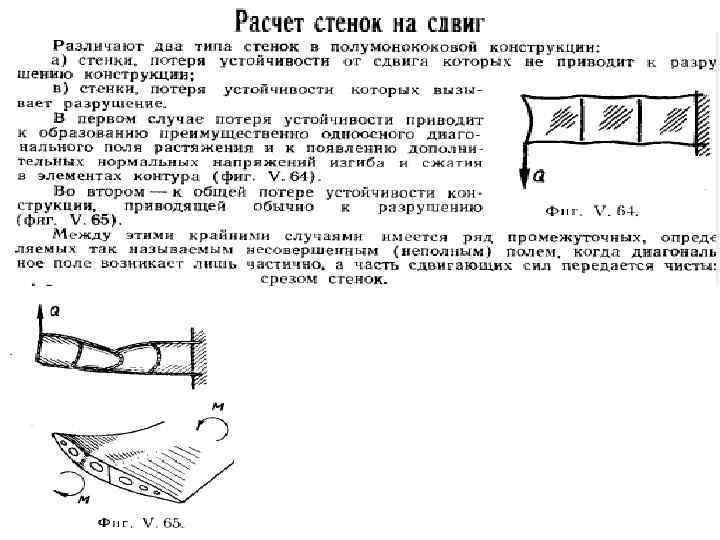
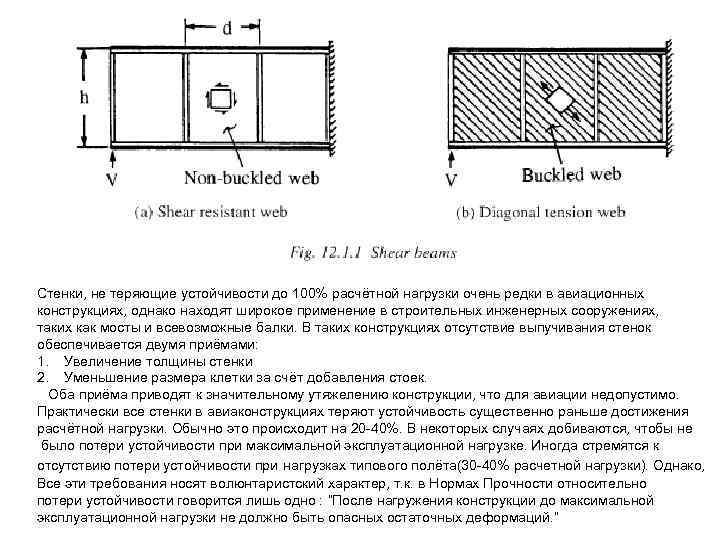Стенки, не теряющие устойчивости до 100% расчётной нагрузки очень редки в авиационных конструкциях, однако находят широкое применение в строительных инженерных сооружениях, таких как мосты и всевозможные балки. В таких конструкциях отсутствие выпучивания стенок обеспечивается двумя приёмами: 1. Увеличение толщины стенки 2. Уменьшение размера клетки за счёт добавления стоек. Оба приёма приводят к значительному утяжелению конструкции, что для авиации недопустимо. Практически все стенки в авиаконструкциях теряют устойчивость существенно раньше достижения расчётной нагрузки. Обычно это происходит на 20 -40%. В некоторых случаях добиваются, чтобы не было потери устойчивости при максимальной эксплуатационной нагрузке. Иногда стремятся к отсутствию потери устойчивости при нагрузках типового полёта(30 -40% расчетной нагрузки). Однако, Все эти требования носят волюнтаристский характер, т. к. в Нормах Прочности относительно потери устойчивости говорится лишь одно : “После нагружения конструкции до максимальной эксплуатационной нагрузки не должно быть опасных остаточных деформаций. ”

Shear Resistant Beams Are Beams Whose Webs Remain Unbuckled Under the Applied Loads t Type II fs = V ht M failure Higher strength Type III Web shear stress allowable, F s IDT Type I sheer resistant Thick webs Web shear buckling stress, F scr h t Thin webs h V h = Height between chord centroids t = Web thickness = Stiffener spacing V = Shear load M = Bending moment f = Average web shear stress s

Advantages and Disadvantages of Shear Resistant Beams Advantages • • • Greater shear stiffness (higher when web remains unbuckled) Nonwrinkling webs reduce potential for fuel leaking (spars and tank end ribs) Easier to analyze (simple theory) Analysis methods are better understood and less empirical Disadvantages • Shear resistant beams tend to be heavier than IDT beams (shear resistant, i. e. , nonbuckling, webs usually thicker than IDT webs—full web postbuckling strength not used)

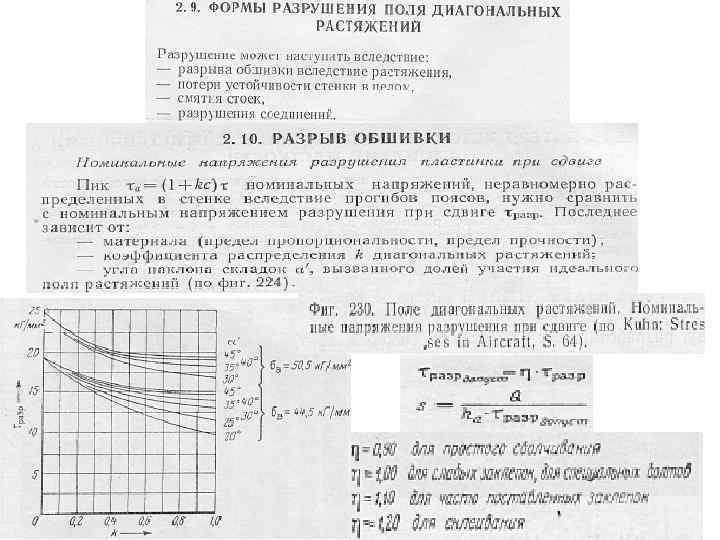
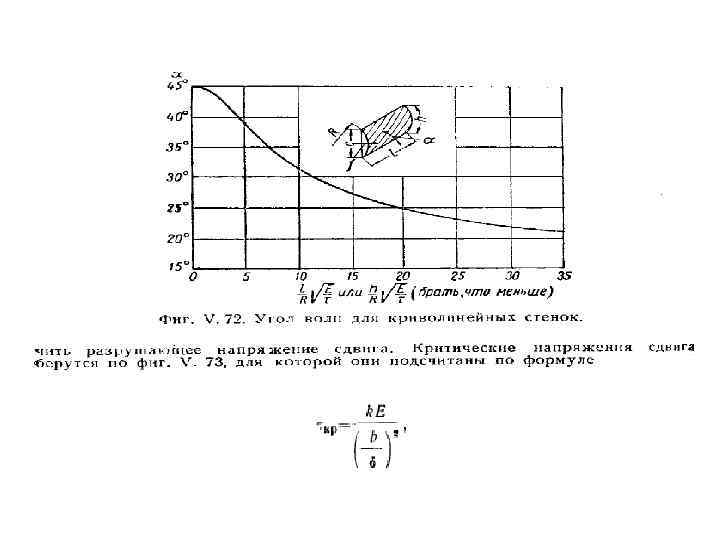
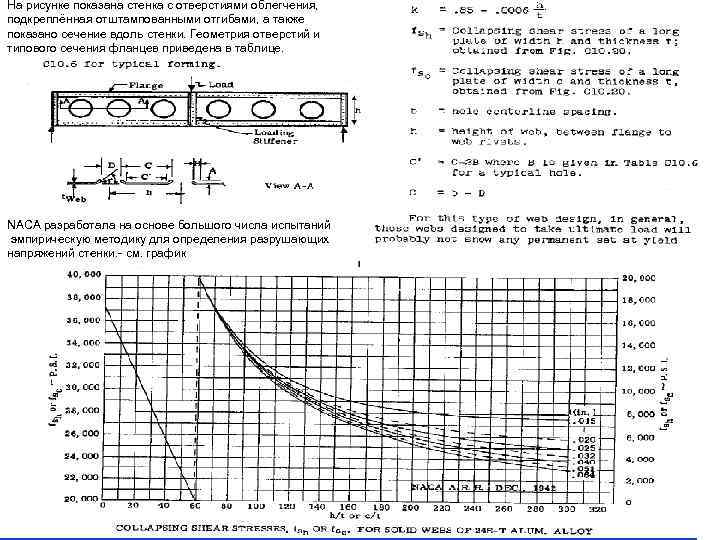На рисунке показана стенка с отверстиями облегчения, подкреплённая отштампованными отгибами, а также показано сечение вдоль стенки. Геометрия отверстий и типового сечения фланцев приведена в таблице. NACA разработала на основе большого числа испытаний эмпирическую методику для определения разрушающих напряжений стенки. - см. график

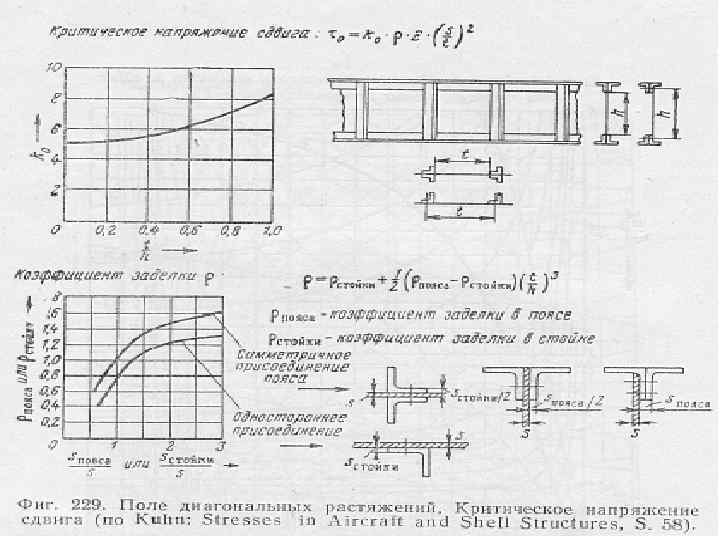
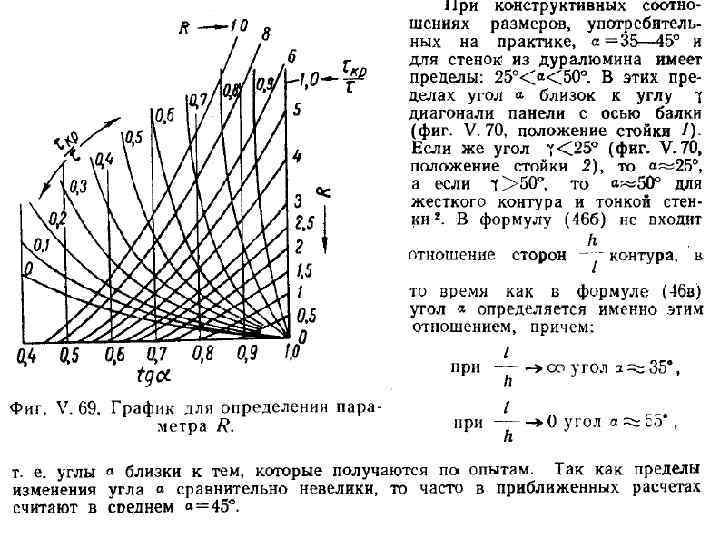
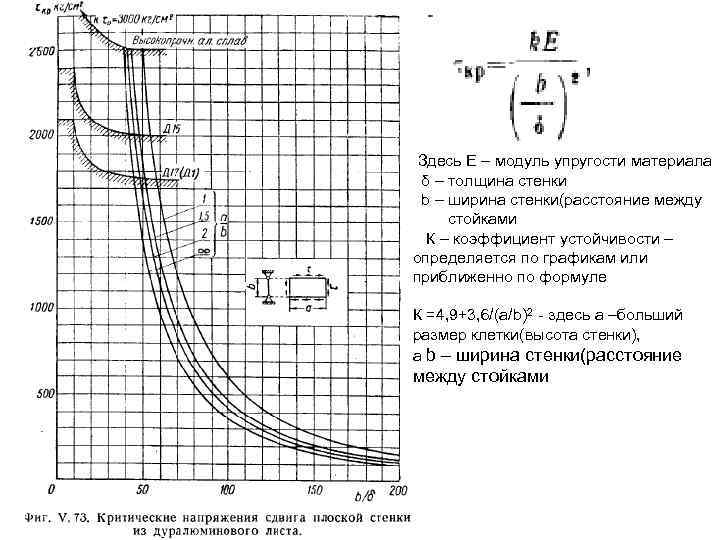Здесь Е – модуль упругости материала δ – толщина стенки b – ширина стенки(расстояние между стойками К – коэффициент устойчивости – определяется по графикам или приближенно по формуле К =4, 9+3, 6/(а/b)2 - здесь а –больший размер клетки(высота стенки), а b – ширина стенки(расстояние между стойками

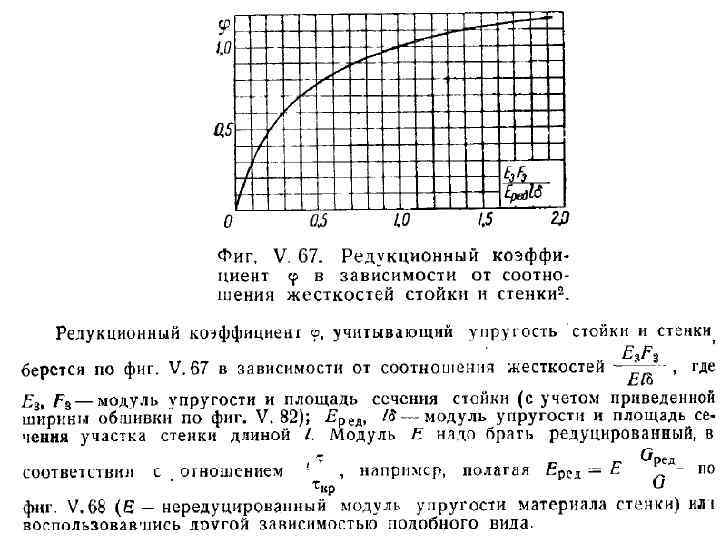
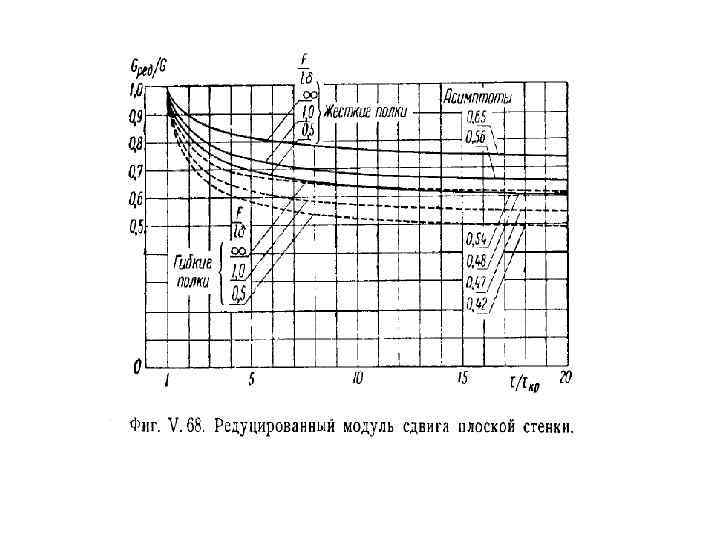
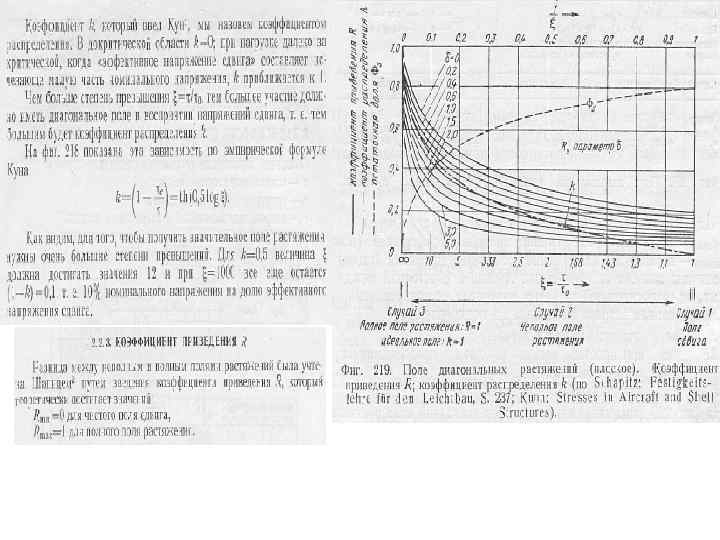
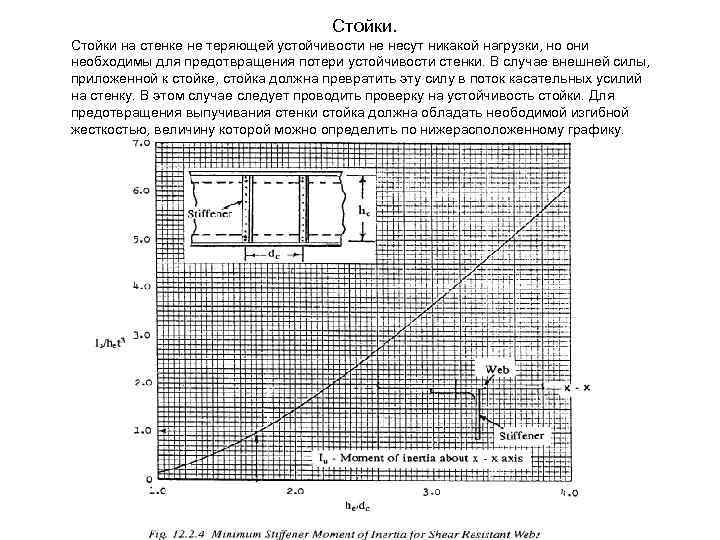Стойки на стенке не теряющей устойчивости не несут никакой нагрузки, но они необходимы для предотвращения потери устойчивости стенки. В случае внешней силы, приложенной к стойке, стойка должна превратить эту силу в поток касательных усилий на стенку. В этом случае следует проводить проверку на устойчивость стойки. Для предотвращения выпучивания стенки стойка должна обладать неободимой изгибной жесткостью, величину которой можно определить по нижерасположенному графику.

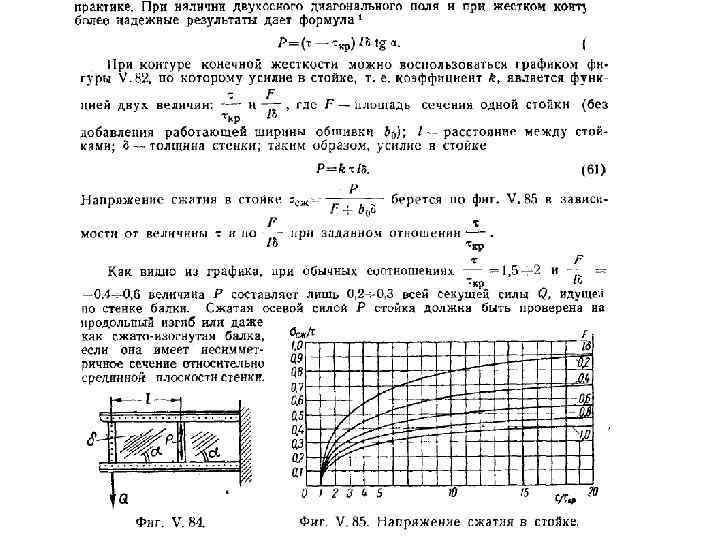
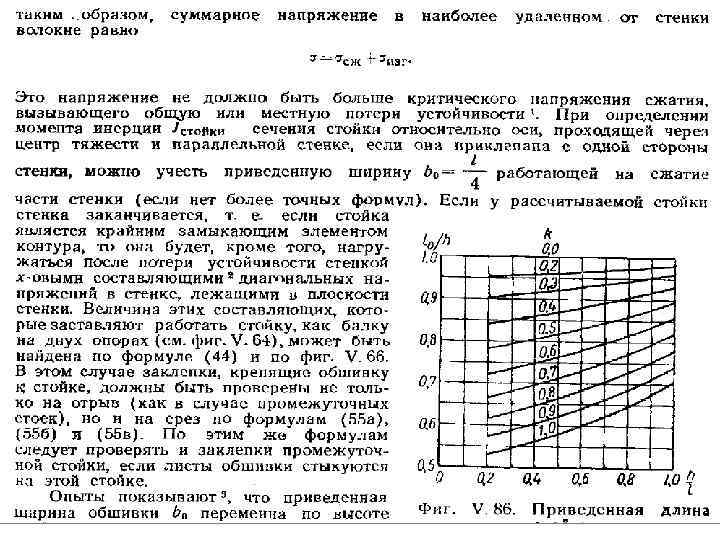
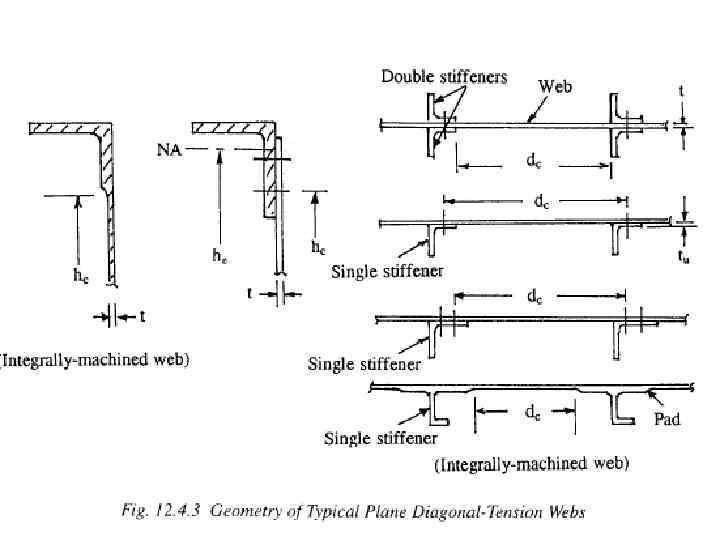
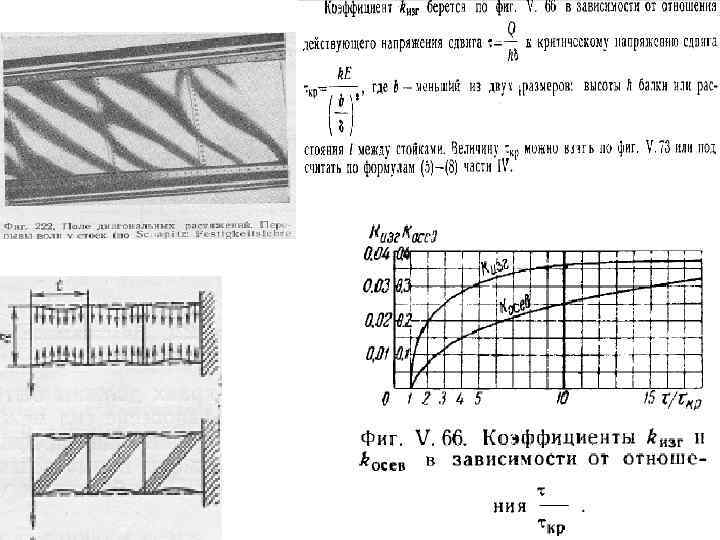
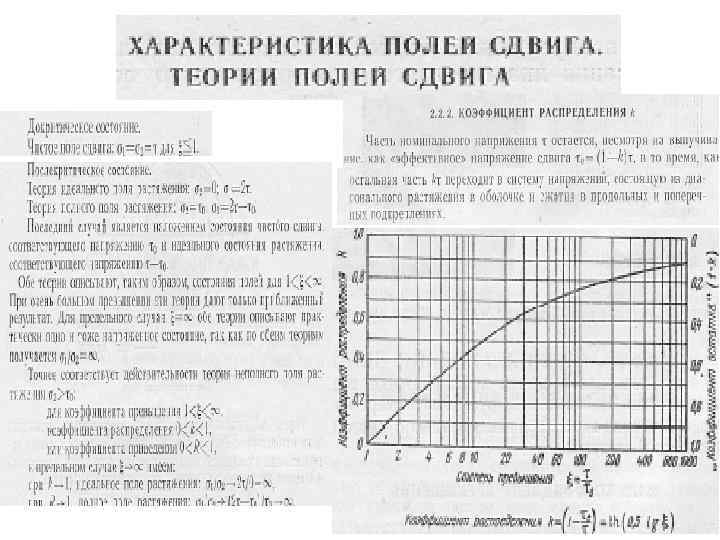
Как образуется диагональное поле растяжения Пусть прямоугольная стенка состоит из пластины, краевых стержней и стоек. Она нагружена усилиями сдвига параллельно краям. В чистом поле сдвига напряжения сдвига τ, перпендикулярные другу, соответствуют наклоненным к ним под углом 45° и также взаимоперпендикулярных главному напряжению растяжения σ1 и главному напряжению сжатия σ2, причем т=σ1=-σ2. Когда напряжения сдвига в пластине достигнет критического значения то, на пластине начинают образовываться складки, направление которых примерно соответствует направлению главных растягивающих напряжений. С образованием складок способность пластины выдерживать напряжения сжатия падает. При этом, однако, несущая способность стенки не исчерпывается. Вследствие образования диагонального поля растяжения стойки начинают работать на сжатие. Первые исследования по обрзованию диагональных растяжений были опубликованы Роде. Заслугой Герберта Вагнера является исчерпывающие исследования идеального поля диагональных растяжений и введение его в науку о прочности тонкостенных конструкций.

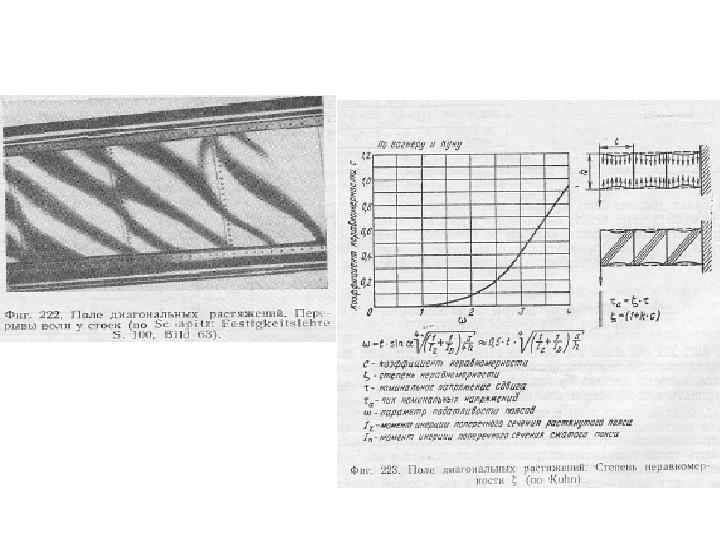
На рисунке показана схема уравновешивания малого треугольного сегмента стенки, вырезанного около верхнего пояса балки Нагрузки на заклёпки: Элемент стенки прикреплён к уголковому поясу Заклёпочным швом вдоль линии АВ. Заклёпки подвергаются воздействию двух сил, одна параллельно АВ, а вторая перпендикулярно ей. И каждая сила Равна Результирующая сила таким образом равна И если взять её на единичной длине то результирующая нагрузка Согласно элементарной механике горизонтальные и вертикальные касательные напряжения создают напряжения сжатия и растяжения в площадках, наклоненных на 45° к площадкам сдвигаю Тонкие стенки могут держать до потери устойчивости лишь очень низкие напряжения сжатия на площадке АС. Тогда этими напряжениями можно пренебречь, т. е. fc=0. Это и будет идеальное диагональное поле. Площадка ВС находится под действием растягивающих напряжений, которые стенка может нести со 100%-ной эффективностью. Силы, действующие на элемент, показаны на Fig. C 11. 5 Уравнение равновесия для сегмента: Однако fs = Q / (ht) Тогда погонная нагрузка на заклёпочный шов q = 1. 41 Q / h Нагрузи на стойки. Под действием вертикальных нагрузок от чистого диагональногополя пояса балок стремятся сблизиться. Этому препятствуют стойки. Если мы просуммируем вертикальные составляющие сил диагонального поля на пролете между стойками, мы получим сжимающую силу на стойку.

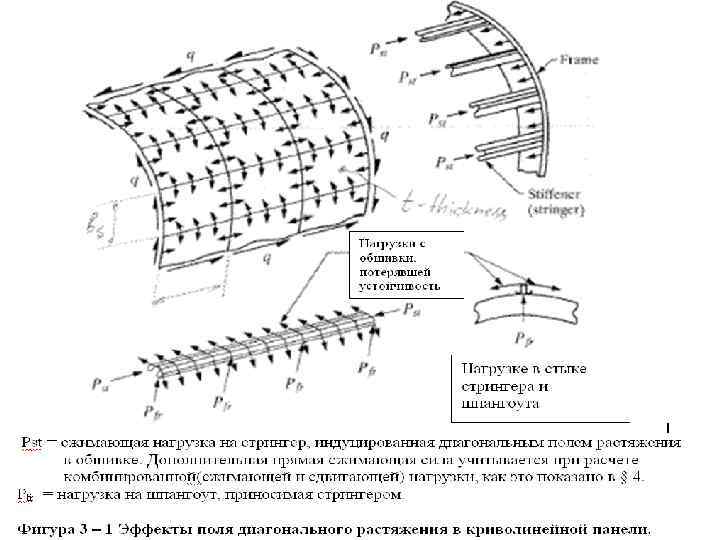
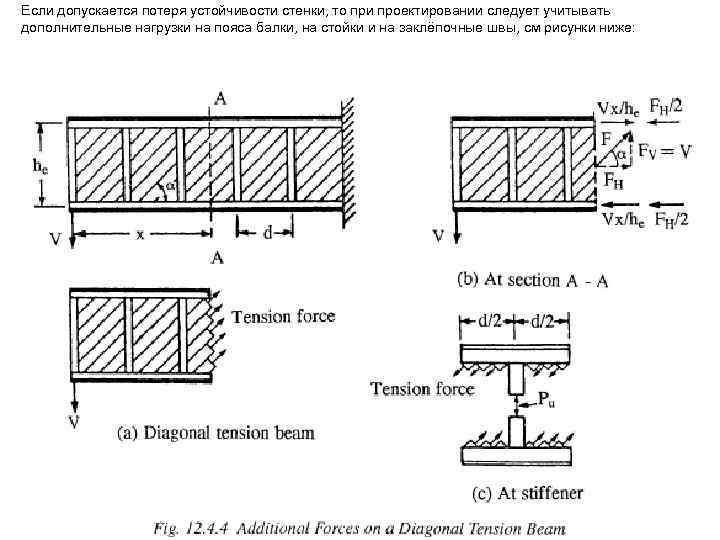Если допускается потеря устойчивости стенки, то при проектировании следует учитывать дополнительные нагрузки на пояса балки, на стойки и на заклёпочные швы, см рисунки ниже: