Ранговые коэффициенты корреляции по Спирмену и Кендаллу Частная

Ранговые коэффициенты корреляции по Спирмену и Кендаллу. Частная корреляция. Мера расстояния и мера сходства. Подготовили: студенты 2 курса 7 группы Минаева Ирина Скукина Татьяна Филимонова Мария Фомиченко Мария Дженабу

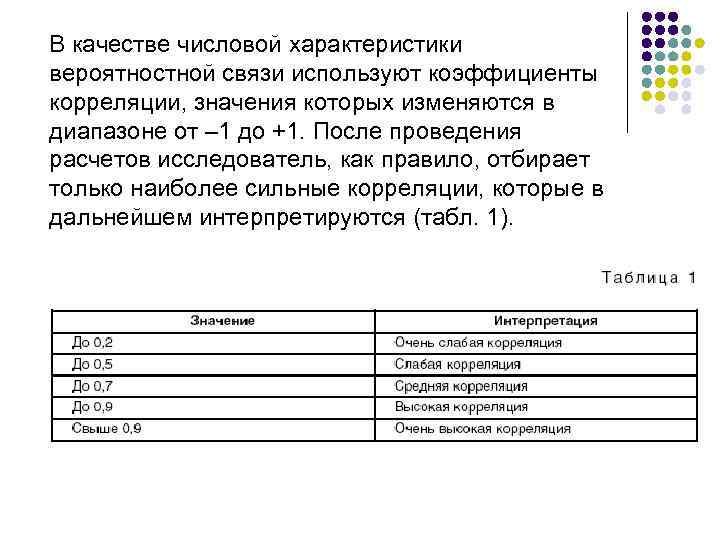В качестве числовой характеристики вероятностной связи используют коэффициенты корреляции, значения которых изменяются в диапазоне от – 1 до +1. После проведения расчетов исследователь, как правило, отбирает только наиболее сильные корреляции, которые в дальнейшем интерпретируются (табл. 1).

l Критерием для отбора «достаточно сильных» корреляций может быть как абсолютное значение самого коэффициента корреляции (от 0, 7 до 1), так и относительная величина этого коэффициента, определяемая по уровню статистической значимости (от 0, 01 до 0, 1), зависящему от размера выборки.

l l Коэффициент Спирмена - один из коэффициентов ранговой корреляции. Используется для измерения взаимосвязи качественных признаков, измеренных по ранговой шкале. Коэффициент ранговой корреляции τКендалла является самостоятельным оригинальным методом, опирающимся на вычисление соотношения пар значений двух выборок, имеющих одинаковые или отличающиеся тенденции.

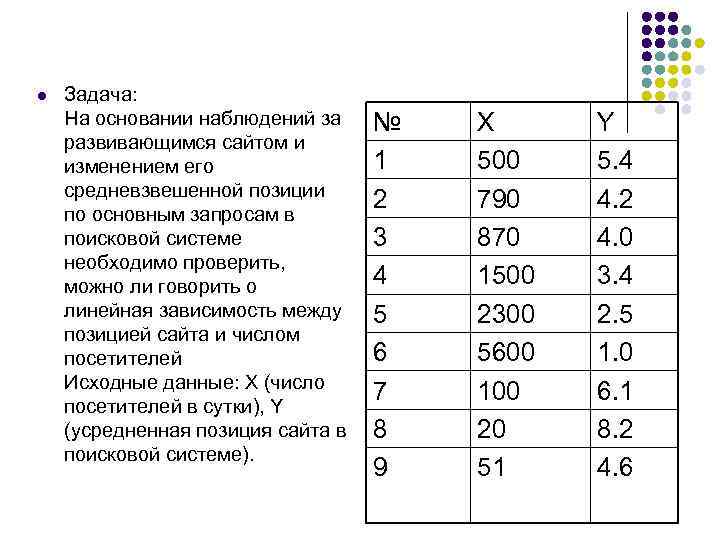l Задача: На основании наблюдений за развивающимся сайтом и изменением его средневзвешенной позиции по основным запросам в поисковой системе необходимо проверить, можно ли говорить о линейная зависимость между позицией сайта и числом посетителей Исходные данные: X (число посетителей в сутки), Y (усредненная позиция сайта в поисковой системе). № 1 2 3 4 5 6 7 8 9 X 500 790 870 1500 2300 5600 100 20 51 Y 5. 4 4. 2 4. 0 3. 4 2. 5 1. 0 6. 1 8. 2 4. 6

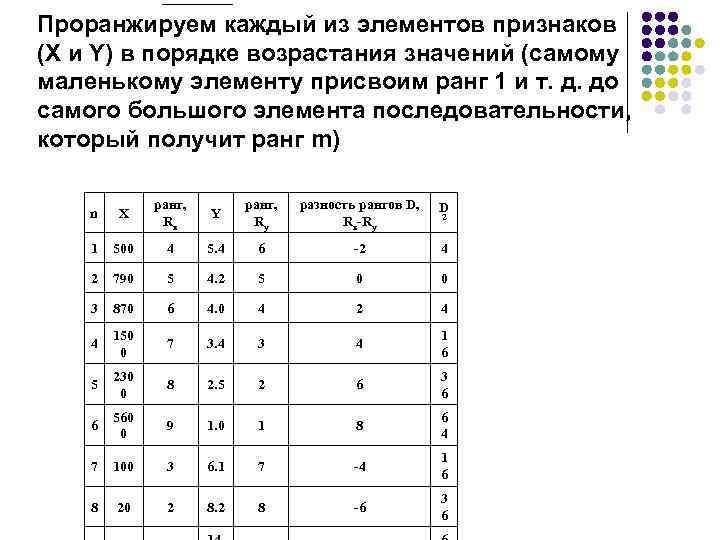Проранжируем каждый из элементов признаков (X и Y) в порядке возрастания значений (самому маленькому элементу присвоим ранг 1 и т. д. до самого большого элемента последовательности, который получит ранг m) n X ранг, Rx Y ранг, Ry разность рангов D, Rx-Ry D 1 500 4 5. 4 6 -2 4 2 790 5 4. 2 5 0 0 3 870 6 4. 0 4 2 4 4 150 0 7 3. 4 3 4 1 6 5 230 0 8 2. 5 2 6 3 6 6 560 0 9 1. 0 1 8 6 4 7 100 3 6. 1 7 -4 1 6 8 20 2 8 -6 3 6 2

Для расчета коэффициента ранговой корреляции Спирмена используется формула: Найдем сумму квадратов разностей рангов, сложив для этого элементы столбца D 2: ∑D 2=240. Коэффициент корреляции Спирмена: ρ=1 -(6*240)/(9*(81 -1)=-1

l l Коэффициент ранговой корреляции Кендалла является альтернативой методу Спирмена. Он предназначен для определения взаимосвязи между двумя ранговыми переменными. Интерпретация результатов вычисления коэффициент ранговой корреляции Кендалла определяется как разность вероятностей совпадения и инверсии в рангах.

коэффициента Кендалла l По данным об объеме строительномонтажных работ, выполненных собственными силами, и численности работающих в 10 строительных компаниях одного из городов РФ, определить зависимость между этими признаками с помощью коэффициента Кендела.

l Присвоим ранги признаку Y и фактору X. Расположим объекты так, чтобы их ранги по X представили натуральный ряд. Так как оценки, приписываемые каждой паре этого ряда, положительные, значения «+1» , входящие в Р, будут порождаться только теми парами, ранги которых по Y образуют прямой порядок. Их легко подсчитать, сопоставляя последовательно ранги каждого объекта в ряду Y с стальными.

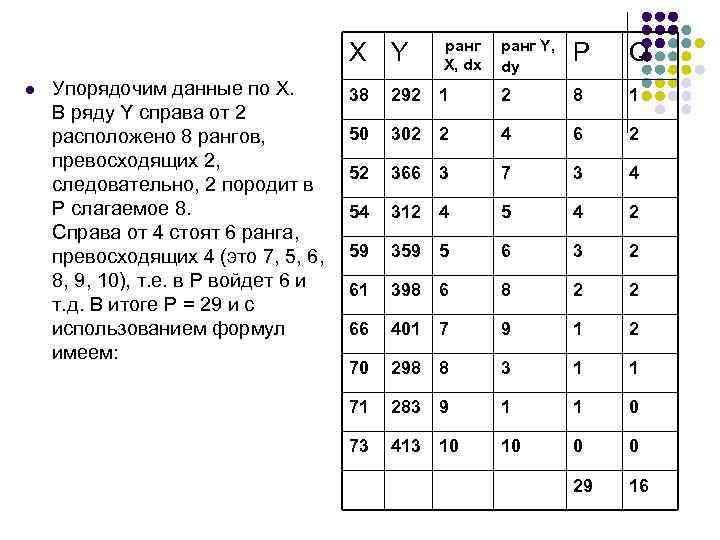X Y l Упорядочим данные по X. В ряду Y справа от 2 расположено 8 рангов, превосходящих 2, следовательно, 2 породит в Р слагаемое 8. Справа от 4 стоят 6 ранга, превосходящих 4 (это 7, 5, 6, 8, 9, 10), т. е. в Р войдет 6 и т. д. В итоге Р = 29 и с использованием формул имеем: ранг Y, X, dx dy P Q 38 292 1 2 8 1 50 302 2 4 6 2 52 366 3 7 3 4 54 312 4 5 4 2 59 359 5 6 3 2 61 398 6 8 2 2 66 401 7 9 1 2 70 298 8 3 1 1 71 283 9 1 1 0 73 413 10 10 0 0 29 16

Найдем коэффициент Кендалла:

Частная корреляция Если исследовать достаточно большую совокупность мужчин и сопоставить размер их обуви с уровнем образованности, то между этими двумя переменными можно заметить хоть и небольшую, но в то же время значимую корреляцию.

Здесь статистически значимый коэффициент корреляции является не проявлением некоторой причинной связи между двумя рассматриваемыми переменными, а в большей степени обусловлен некоторой третьей переменной. . С одной стороны существует некоторая незначительная корреляция между ростом и уровнем образованности, а с другой — вполне объяснимая и логичная связь между ростом и размером обуви. Вместе эти две корреляции приводят к упоминавшейся ложной корреляции. Для исключения одной такой искажающей переменной необходим расчёт так называемой частной корреляции.

l В то время как линейный коэффициент корреляции — это показатель силы связи, описывающий линейную зависимость между двумя переменными, частный коэффициент корреляции — это мера зависимости между двумя переменными при фиксированных (исключенных) или скорректированных эффектах одной или нескольких переменных.

Мера расстояния и мера сходства l l Существует 4 вида коэффициента сходства: коэффициента корреляции, меры расстояния, коэффициента ассоциативности и вероятностные коэффициенты сходства. Для вычисления расстояния между объектами используются различные меры сходства (меры подобия), называемые также метриками или функциями расстояний.

Квадрат евклидова расстояния. Для придания больших весов более отдаленным друг от друга объектам можем воспользоваться квадратом евклидова расстояния путем возведения в квадрат стандартного евклидова расстояния. l Манхэттенское расстояние (расстояние городских кварталов), также называемое "хэмминговым" или "сити-блок" расстоянием. Это расстояние рассчитывается как среднее разностей по координатам. l